Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.
Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:
Внешний алфавит. Конечное множество (обозначают буквой А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ.
Например, алфавит машины Тьюринга, работающей с двоичными числами, задается в виде A = .
Непрерывную цепочку символов на ленте называют словом.
Автоматом называют устройство, работающее без участия человека. Автомат в машине Тьюринга имеет несколько состояний и при определенных условиях переходит из одного состояния в другое. Множество состояний автомата называют внутренним алфавитом.
Теория алгоритмов: машина Тьюринга
Внутренний алфавит. Конечное множество состояний каретки (автомата). Обозначается буквой Q=. Одно из состояний — q1- должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние остановка.
Таблица переходов. Описание поведения автомата (каретки) в зависимости от состояния и считанного символа.
Автомат машины Тьюринга в процессе своей работы управляется программой, во время каждого шага которой выполняются последовательно следующие действия:
— Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).
— Передвигаться на одну ячейку влево или вправо.
— Менять свое внутреннее состояние.
Поэтому при составлении программы для каждой пары (символ, состояние) нужно определить три параметра: символ ai из выбранного алфавита A, направление перемещения каретки («←” — влево, «→” — вправо, «точка” — нет перемещения) и новое состояние автомата qk.
Например, команда 1 «←” q2 обозначает «заменить символ на 1, переместить каретку влево на одну ячейку и перейти в состояние q2”.
Предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.
Вопрос 28
Тезис Тьюринга — принимаемое без доказательства фундаментальное положение теории алгоритмов, согласно которому всякий алгоритм представим в форме машины Тьюринга.
Программа машины Тьюринга (Р) — совокупность всех команд, Программа представляется в виде таблицы и называется Тьюринговой функциональной схемой.
| a0 | a1 | a2 | |
| q1 | а0Пq1 | a1Пq1 | a2Лq2 |
| q2 | а1Пq2 | a2Нq0 | a0Нq0 |
Машина Тьюринга (видеоурок)

Вопрос 29
Машины Тьюринга с двумя выходами
Предположим, мы расширили определение машины Тьюринга, добавив в устройство управления машины определенное состояние q*. Будем говорить, что если устройство управления переходит в состояние q0 для заданного входного слова х, то машина допускает х. Если устройство управления приходит в состояние q *, то машина запрещает х. Такое устройство будем называть машиной Тьюринга с двумя выходами.
Оказывается, что если заданы две машины Тьюринга T1 и Т2, которые допускают непересекающиеся множества слов Х1 и Х2 соответственно, то всегда можно построить машину Тьюринга T3 с двумя выходами, которая будет допускать Х1 и запрещать Х2. Эти машины Тьюринга будут нам полезны при рассмотрении вопроса о разрешимости.
Множество разрешимо, если существует машина Тьюринга с двумя выходами, которая допускает все элементы этого множества и запрещает элементы, не принадлежащие ему.
Вопрос 30
Многоленточная машина Тьюринга состоит из конечного управления с k ленточными головками, по одной на каждой ленте (рис. 6.4).
Каждая лента бесконечна в обоих направлениях. При одном движении, зависящем от состояния конечного управления и сканируемого символа каждой из ленточных головок, машина может: 1) изменить состояние; 2) напечатать новый символ на каждой из сканируемых ячеек; 3) передвинуть каждую из ее ленточных головок независимо друг от друга на одну ячейку влево, вправо или оставить ее на том же месте.
Сначала входная цепочка имеется только на первой ленте, а все другие лен- ты пусты. Мы не будем определять это устройство более формально, предоставляя это читателю.
Теорема 6.2. Если язык L принимается многоленточной машиной Тьюринга, то он принимается одноленточной машиной Тьюринга. Доказательство. Пусть язык L принимается машиной Тьюринга T1 с k лентами. Построим одноленточную машину Тьюринга T2 с 2k дорожками, по две для каждой из лент машины T1.
На одной дорожке записывается содержимое соответствующей ленты машины T1, а другая — пустая, за исключением маркера в ячейке, содержащей символ и сканируемой соответствующей головкой машины T1. Такое устройство для моделирования трех лент посредством одной иллюстрируется рис. 6.5. Конечное управление машины T2 запоминает, какие маркеры головок машины T1 находятся слева, а какие — справа от головки T2. Состояния машины T1 тоже запоминаются в конечном управлении машины T2.
Чтобы моделировать движение машины T1, машина T2 должна посетить каждую ячейку с маркером головки, регистрируя по очереди символ, сканируемый соответствующей головкой T1. Когда машина T2 проходит через маркер головки, она должна уточнять направление, в котором следует искать этот маркер. После сбора всей необходимой информации машина T2 определяет движение машины T1. Затем машина T2 посещает по очереди каждый из маркеров головок снова, изменяя маркированные ячейки и сдвигая маркеры на одну ячейку, если необходимо. Конечно, если новое состояние является принимающим, то машина T2 принимает входную цепочку.
Вопрос 31
Источник: megalektsii.ru
Лабораторная работа «Разработка программ для машины Тьюринга»
Цель: научится строить машины Тьюринга на специальном тренажере для изучения универсального исполнителя.
Эмулятор машины Тьюринга
Что такое машина Тьюринга?
Машина Тьюринга — это универсальный исполнитель (абстрактная вычислительная машина), предложенный английским математиком А. Тьюрингом в 1936 году как уточнения понятия алгоритма. Согласно тезису Тьюринга, любой алгоритм может быть записан в виде программы для машины Тьюринга.
Машина Тьюринга состоит из каретки (считывающей и записывающей головки) и бесконечной ленты, разбитой на ячейки. Каждая ячейка ленты может содержать символ из некоторого алфавита A = a0,a1,…,aN> . Любой алфавит содержит символ «пробел», который обозначается как a0 или L.
Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = q0,q1,…,qM>. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· новое состояние автомата
При вводе команд пробел заменяется знаком подчеркивания «_».
Как работать с программой?
В верхней части программы находится поле редактора, в которое можно ввести условие задачи в свободной форме.
Лента перемещается влево и вправо с помощью кнопок, расположенных слева и справа от нее. Двойным щелчком по ячейке ленты (или щелчком правой кнопкой мыши) можно изменить ее содержимое.
С помощью меню Лента можно запомнить состояние ленты во внутреннем буфере и восстановить ленту из буфера.
В поле Алфавит задаются символы выбранного алфавита. Пробел добавляется к введенным символам автоматически.
В таблице в нижней части окна набирается программа. В первом столбце записаны символы алфавита, он заполняется автоматически. В первой строке перечисляются все возможные состояния. Добавить и удалить столбцы таблицы (состояния) можно с помощью кнопок, расположенных над таблицей.
При вводе команды в ячейку таблицы сначала нужно ввести новый символ, затем направление перехода и номер состояния. Если символ пропущен, по умолчанию он не изменяется. Если пропущен номер состояния, по умолчанию состояние автомата не изменяется.
Справа в поле Комментарий можно вводить в произвольной форме комментарии к решению. Чаще всего там объясняют, что означает каждое состояние машины Тьюринга.
Программа может выполняться непрерывно (F9) или по шагам (F8). Команда, которая сейчас будет выполняться, подсвечивается зеленым фоном. Скорость выполнения регулируется с помощью меню Скорость.
Задачи для машины Тьюринга можно сохранять в файлах. Сохраняется условие задачи, алфавит, программа, комментарии и начальное состояние ленты. При загрузке задачи из файла и сохранении в файле состояние ленты автоматически записывается в буфер.
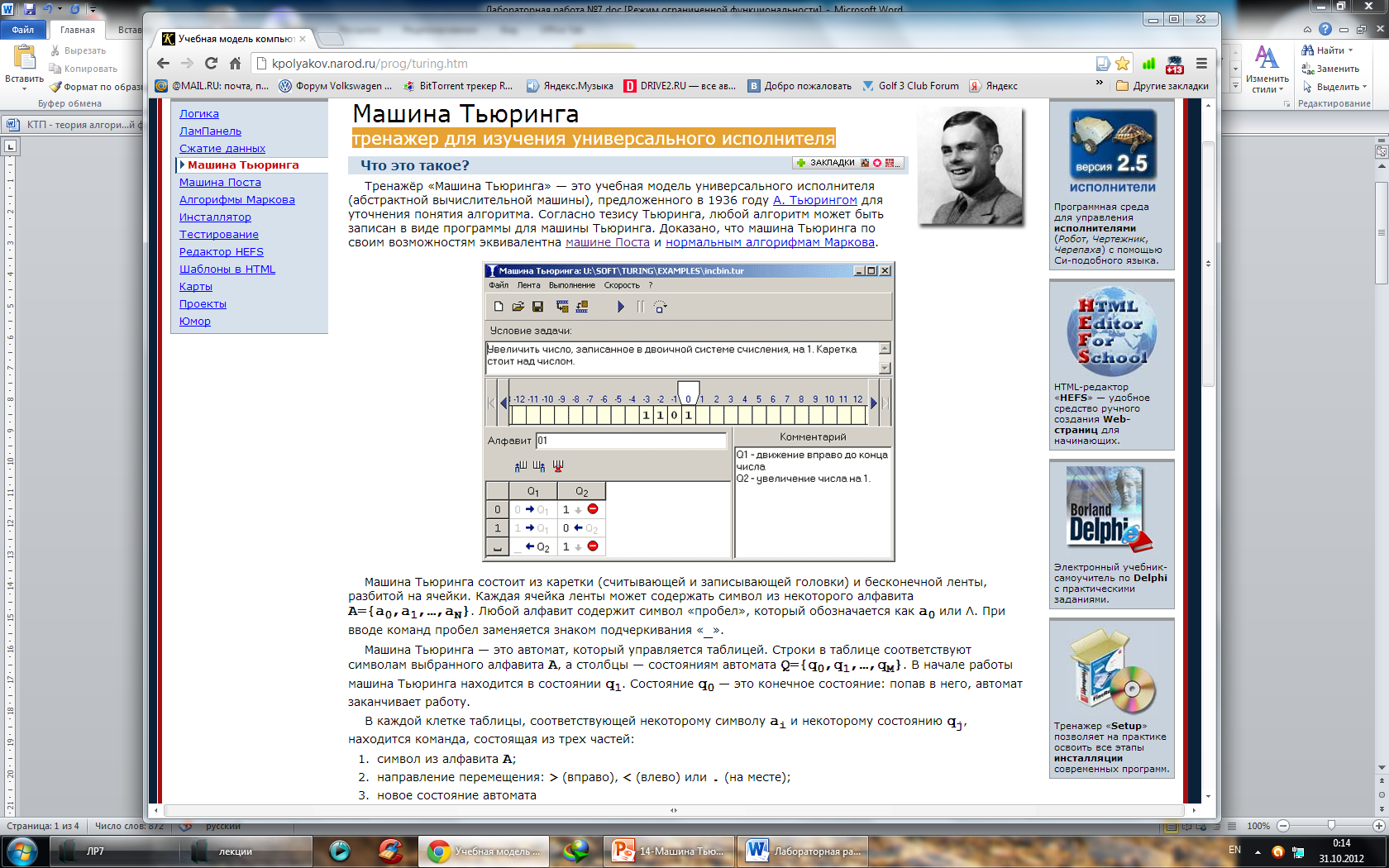
Пример 1. Написать машину Тьюринга, которая исправляет ошибку в слове «малако».
- Запускаем программу turing.exe.
- Вносим символы «аклмо» в алфавит программы.
- На ленте начиная с позиции «0» вводим слово «малако».
- Удаляем ненужные столбцы Q кнопкой .
- Заполняем таблицу командами.
- >1
- >1
- >1
- >1
- >1
- Запускаем программу.
Задание 1.
Вариант 1
Вариант 2
Написать машину Тьюринга, которая исправляет ошибку в слове «пороллилагромм».
Написать машину Тьюринга, которая исправляет ошибку в слове «иксковотар».
Задание 2. Дано натуральное число n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, т.е. выполняла функцию , при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q1 обозревает правую цифру числа.
Состояние q1 — уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения — сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q2.
Состояние q2 — после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a0).
Состояние q3 — если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова.
Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.
Задание 3.
Вариант 1
Вариант 2
Реализовать на эмуляторе машины Тьюринга алгоритм вычисления функции .
Вычислите
Реализовать на эмуляторе машины Тьюринга алгоритм вычисления функции .
Вычислите
Задание 4. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “( )”.
Например, дано “) ( ( ) ( ( )”, надо получить “). ( ( ”.
Автомат в состоянии q1 обозревает крайний левый символ строки.
Ключ к заданию.
Задание 5. Оформите отчет, записав в него таблицы (программы) для машин Тьюринга из заданий №1, №3 и №4.
Герасимова Светлана Александровна
Содержимое разработки
Лабораторная работа №7
Тема: «Разработка программ для машины Тьюринга»
Цель: научится строить машины Тьюринга на специальном тренажере для изучения универсального исполнителя.
Эмулятор машины Тьюринга
Что такое машина Тьюринга?
Машина Тьюринга — это универсальный исполнитель (абстрактная вычислительная машина), предложенный английским математиком А. Тьюрингом в 1936 году как уточнения понятия алгоритма. Согласно тезису Тьюринга, любой алгоритм может быть записан в виде программы для машины Тьюринга.
Машина Тьюринга состоит из каретки (считывающей и записывающей головки) и бесконечной ленты, разбитой на ячейки. Каждая ячейка ленты может содержать символ из некоторого алфавита A = a0,a1,…,aN> . Любой алфавит содержит символ «пробел», который обозначается как a0 или .
Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = q0,q1,…,qM>. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
символ из алфавита A
направление перемещения: « » (вправо), «» (влево) или «.» (на месте)
новое состояние автомата
При вводе команд пробел заменяется знаком подчеркивания «_».
Как работать с программой?
В верхней части программы находится поле редактора, в которое можно ввести условие задачи в свободной форме.
Лента перемещается влево и вправо с помощью кнопок, расположенных слева и справа от нее. Двойным щелчком по ячейке ленты (или щелчком правой кнопкой мыши) можно изменить ее содержимое.
С помощью меню Лента можно запомнить состояние ленты во внутреннем буфере и восстановить ленту из буфера.
В поле Алфавит задаются символы выбранного алфавита. Пробел добавляется к введенным символам автоматически.
В таблице в нижней части окна набирается программа. В первом столбце записаны символы алфавита, он заполняется автоматически. В первой строке перечисляются все возможные состояния. Добавить и удалить столбцы таблицы (состояния) можно с помощью кнопок, расположенных над таблицей.
При вводе команды в ячейку таблицы сначала нужно ввести новый символ, затем направление перехода и номер состояния. Если символ пропущен, по умолчанию он не изменяется. Если пропущен номер состояния, по умолчанию состояние автомата не изменяется.
Справа в поле Комментарий можно вводить в произвольной форме комментарии к решению. Чаще всего там объясняют, что означает каждое состояние машины Тьюринга.
Программа может выполняться непрерывно (F9) или по шагам (F8). Команда, которая сейчас будет выполняться, подсвечивается зеленым фоном. Скорость выполнения регулируется с помощью меню Скорость.
Задачи для машины Тьюринга можно сохранять в файлах. Сохраняется условие задачи, алфавит, программа, комментарии и начальное состояние ленты. При загрузке задачи из файла и сохранении в файле состояние ленты автоматически записывается в буфер.
Пример 1. Написать машину Тьюринга, которая исправляет ошибку в слове «малако».
- Запускаем программу turing.exe.
- Вносим символы «аклмо» в алфавит программы.
- На ленте начиная с позиции «0» вводим слово «малако».
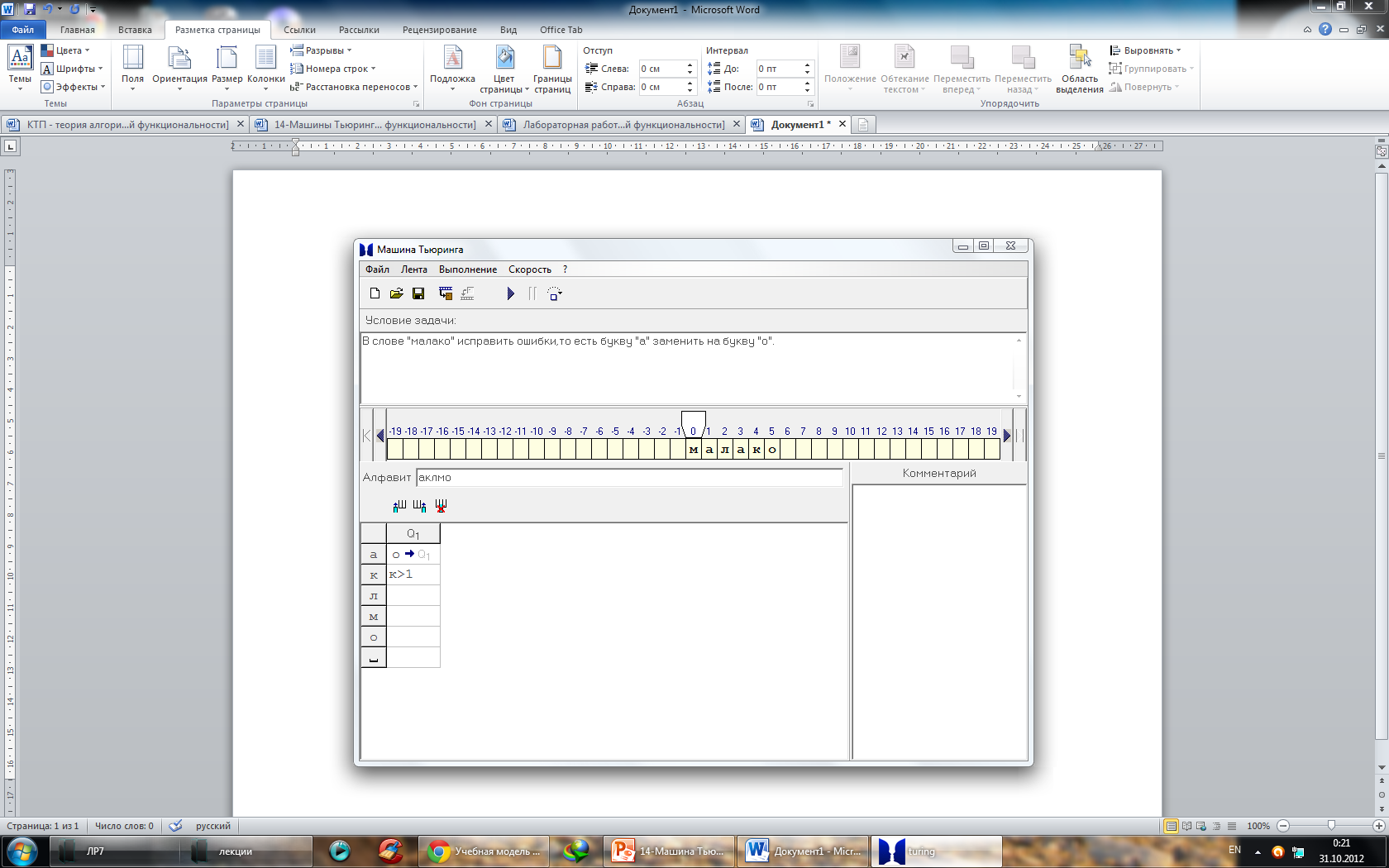
- Удаляем ненужные столбцы Q кнопкой
 .
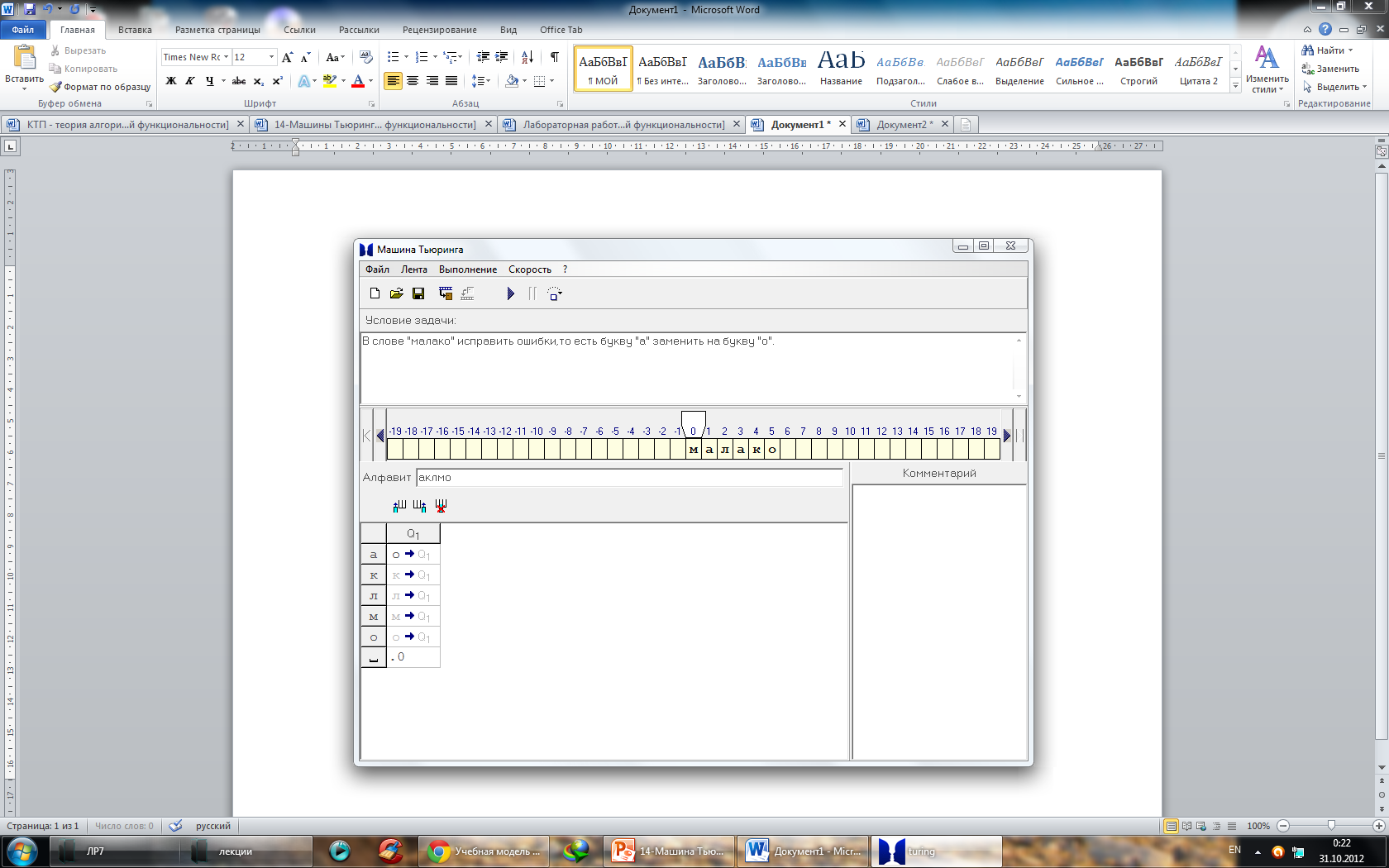
. - Заполняем таблицу командами.
- о1
- к1
- л1
- м1
- о1
- .



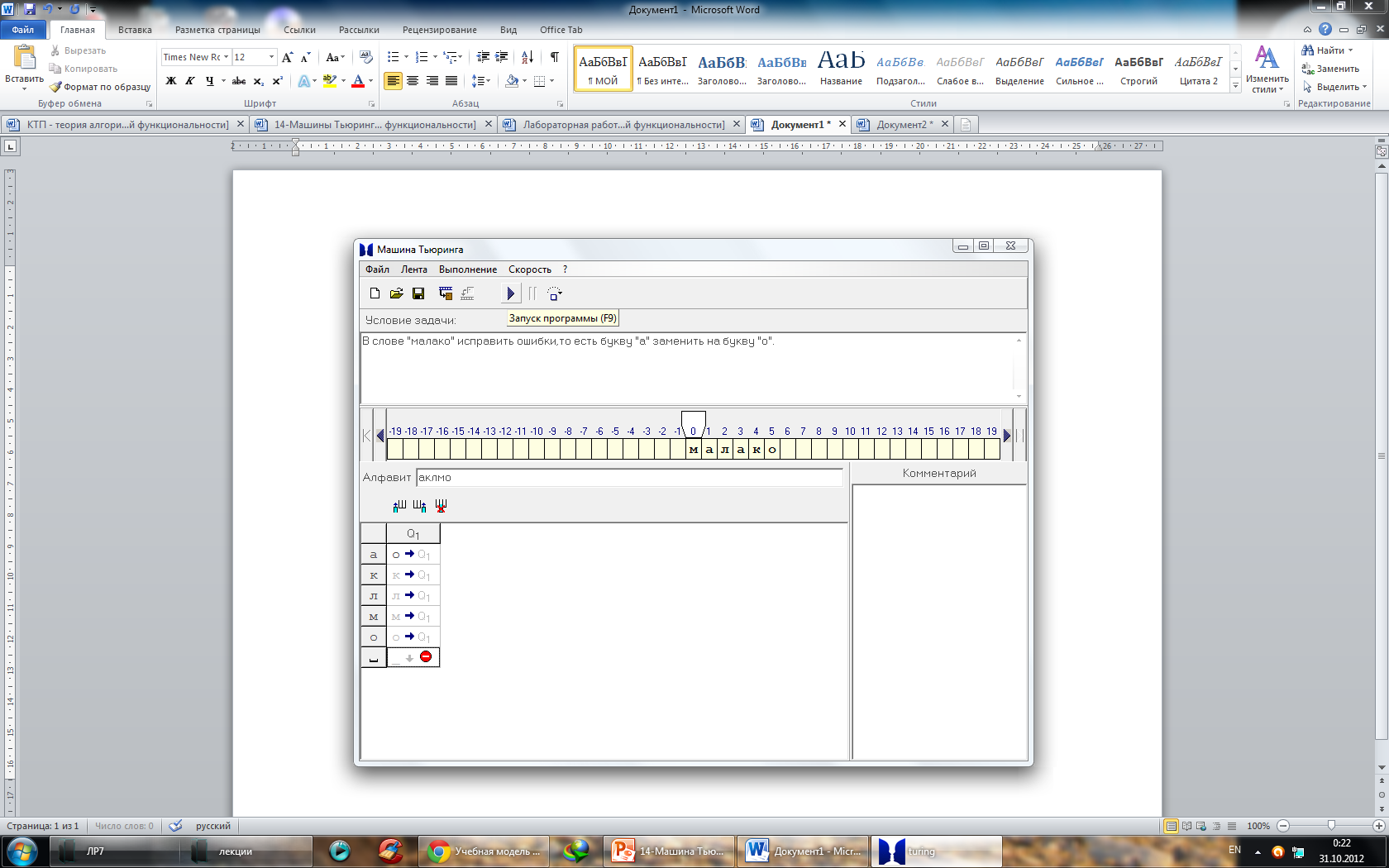
- Запускаем программу.

Задание 1.
| Вариант 1 | Вариант 2 |
| Написать машину Тьюринга, которая исправляет ошибку в слове «пороллилагромм». | Написать машину Тьюринга, которая исправляет ошибку в слове «иксковотар». |
Задание 2. Дано натуральное число n 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, т.е. выполняла функцию 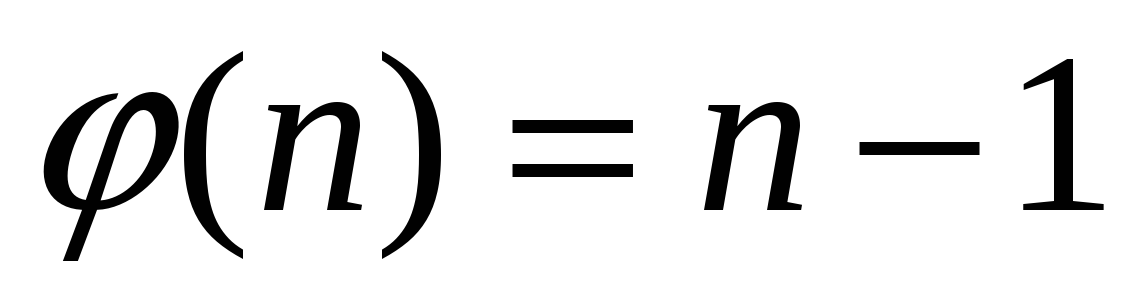 , при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q1 обозревает правую цифру числа.
, при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q1 обозревает правую цифру числа. 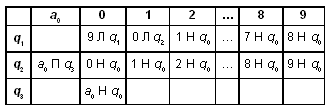 Состояние q1 — уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения — сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q2. Состояние q2 — после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a0). Состояние q3 — если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова. Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.
Состояние q1 — уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения — сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q2. Состояние q2 — после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a0). Состояние q3 — если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова. Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.
Задание 3.
| Вариант 1 | Вариант 2 |
Реализовать на эмуляторе машины Тьюринга алгоритм вычисления функции 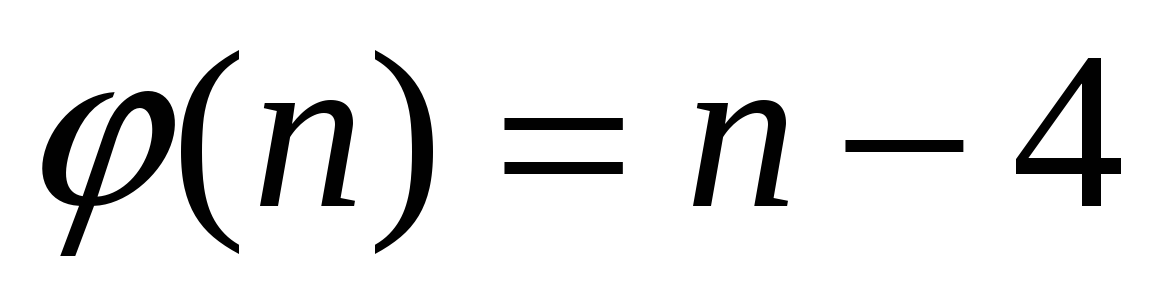 . Вычислите . Вычислите 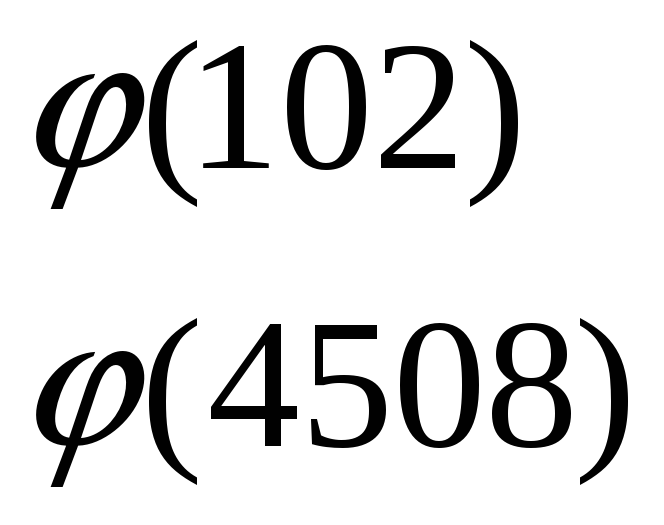 |
Реализовать на эмуляторе машины Тьюринга алгоритм вычисления функции 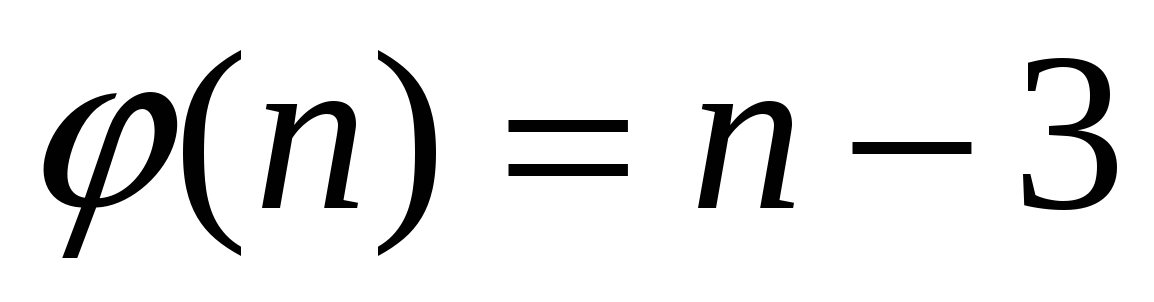 . Вычислите . Вычислите 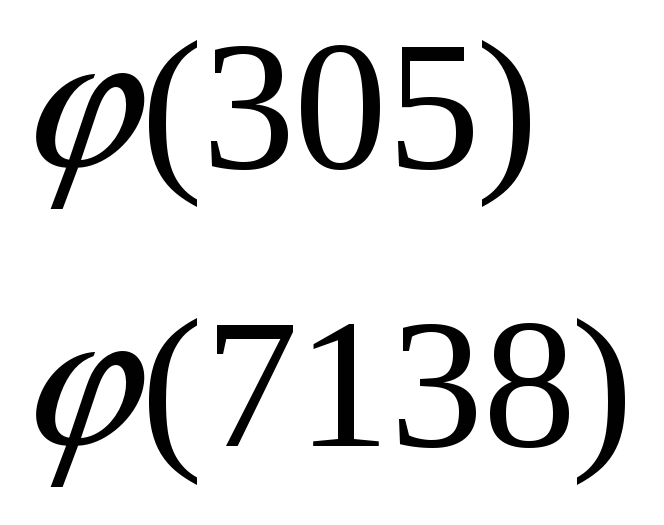 |
Задание 4. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “( )”. Например, дано “) ( ( ) ( ( )”, надо получить “) . . . ( ( ”. Автомат в состоянии q1 обозревает крайний левый символ строки. Ключ к заданию.
- Состояние q1: если встретили “(”, то сдвиг вправо и переход в состояние q2; если встретили “a0”, то останов.
- Состояние q2: анализ символа “(” на парность, в случае парности должны увидеть “)”. Если парная, то возврат влево и переход в состояние q3.
- Состояние q3: стираем сначала “(”, затем “)” и переходим в q1.
Задание 5. Оформите отчет, записав в него таблицы (программы) для машин Тьюринга из заданий №1, №3 и №4.

-82%
Источник: videouroki.net
Программирование машин Тьюринга
Программирование машин Тьюринга — это программирование математической модели вычислений, определяющей абстрактную машину, которая манипулирует символами на полоске ленты в соответствии с таблицей правил.
Введение
Машина Тьюринга считается одним из самых выдающихся научных изобретений прошлого века. Она является несложной и удобной абстрактной моделью вычислительного процесса, представленной в общей форме, и обеспечивает возможность реализации фактически любой компьютерной задачи. Несложное описание и исполненный математический анализ позволили её считать основой теоретической информатики. Это научное исследование послужило стимулом к более глубокому изучению цифрового исчисления и компьютерной техники, включая осознание факта, что есть проблема в области вычислений, которую невозможно решить на стандартных электронных вычислительных машинах пользователей.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Машиной Тьюринга является чёткое математическое построение, то есть математический аппарат, который был создан для решения определенного класса задач. Данному математическому аппарату был присвоено название «машина», так как по описанию его составных частей и принципу действия он является аналогом вычислительной машины. Принципиальным отличием машины Тьюринга от вычислительных машин считается тот факт, что её устройство памяти спроектировано как бесконечная лента, а у существующих вычислительных машин запоминающий блок может иметь какие угодно большие, но обязательно конечные размеры. Машина Тьюринга не может быть реализована как раз по причине бесконечности ее ленты. С этой точки зрения она может считаться более мощной, чем любая вычислительная машина.
Программирование машин Тьюринга
В любой машине Тьюринга должны присутствовать следующие элементы:
- Бесконечная в обоих направлениях лента, которая поделена на ячейки.
- Автоматическая головка для считывания и записи информации, которая управляется программой.
«Программирование машин Тьюринга»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы
Со всеми машинами Тьюринга используется пара конечных алфавитов:
- Алфавит, представляющий входные символы A = .
- Алфавит, представляющий состояния Q = .
Необходимо отметить, что различные машины Тьюринга могут обладать разными алфавитами A и Q. Состояние q0 именуется как пассивное. Принято считать, что когда машина попадает в данное состояние, то это означает, что она окончила свою работу. Состояние q1 принято считать начальным. Именно из этого состояния, машина будет начинать свою работу.
Входное слово должно размещаться на ленте по одному символу в идущих подряд ячейках. Слева и справа от входного слова расположены лишь пустые ячейки. В алфавите А всегда должна находиться пустая буква а0, которая является признаком того, что данная ячейка пустая.
Автомат способен перемещаться вдоль ленты влево или вправо, считывать содержимое ячеек, а также выполнять запись в ячейки буквы. На рисунке ниже представлено схематичное отображение машины Тьюринга, автомат которой работает с первой ячейкой с данными:
Рисунок 1. Схематичное отображение машины Тьюринга. Автор24 — интернет-биржа студенческих работ
Автомат всё время способен «видеть» только одну ячейку. В зависимости от того, какую букву ai он увидел, а также в зависимости от своего состояния qj, автомат может исполнить следующие операции:
- Запись новой буквы в обрабатываемую ячейку.
- Осуществление сдвига по ленте на одну ячейку вправо, влево или вообще не перемещаться.
- Переход в новое состояние.
Таким образом у машины Тьюринга имеется три вида операций. Над каждой ячейкой для какой-либо пары (qj, ai) машина Тьюринга осуществляет исполнение команды, состоящей из трех операций с определенными параметрами.
Программа для машины Тьюринга является, по сути, таблицей, в каждой клетке которой расположена команда, например, как показано на рисунке ниже.
Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ
Клетка (qj, ai) может быть определена двумя параметрами, а именно, алфавитным символом и состоянием машины. Команда представляет собой набор следующих указаний:
- Куда переместить головку для чтения и записи.
- Какой именно символ подлежит записи в текущую ячейку.
- В какое состояние следует перейти машине.
Чтобы обозначить направление перемещения автомата, используется одна из следующих букв:
- «Л» означает перемещение влево.
- «П» означает перемещение вправо.
- «Н» означает неподвижность.
После исполнения автоматом текущей команды, он должен перейти в состояние qm, которое в принципе может таким же, как прежнее состоянием qj. Следующую команду необходимо искать в m-й строке таблицы на пересечении со столбцом al (букву al автомат сможет увидеть после сдвига).
Следует заметить, что когда лента содержит входное слово, то автомат расположен против какой-либо ячейки в состоянии q1. В процессе работы автомат станет перемещаться из одной клетки программы (таблицы) в другую, пока не доберётся до клетки, в которой содержится запись, что автомату следует перейти в состояние q0. Такие клетки носят название клеток останова. При достижении любой такой клетки, машина Тьюринга осуществляет остановку.
Невзирая на достаточно простое устройство, машина Тьюринга способна исполнять все возможные преобразования слов, что позволяет реализовывать различные алгоритмы.
Машина Поста также является абстрактной вычислительной машиной, которая была предложена Эмилем Леоном Постом. Она по сравнению с машиной Тьюринга имеет ещё более простую структуру, но обе эти машины по существу аналогичны и создавались для того, чтобы уточнить понятие «алгоритм».
Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты. Каждая секция ленты способна быть или пустой, что отмечается нулём, или помечаться меткой единица. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит. Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и ее начальное состояние, то есть состояние ленты и позицию каретки.
Источник: spravochnick.ru