Кодирование Хаффмана (также известное как кодирование Хаффмана) — это алгоритм сжатия данных, который формирует основную идею сжатия файлов. В этом посте рассказывается о кодировании с фиксированной и переменной длиной, уникально декодируемых кодах, правилах префиксов и построении дерева Хаффмана.
Обзор
Сжатие данных без потерь. Использование алгоритма Хаффмана
Котиева, Х. М. Сжатие данных без потерь. Использование алгоритма Хаффмана / Х. М. Котиева. — Текст : непосредственный // Молодой ученый. — 2020. — № 35 (325). — С. 12-14. — URL: https://moluch.ru/archive/325/73307/ (дата обращения: 04.07.2023).
Говоря сегодня о сжатии данных, на ум приходит вопрос: а нужно ли оно в наше время? Конечно же, да! Мы знаем, что сейчас нам доступны носители огромного объема и высокоскоростные каналы передачи данных, но нужно учитывать то, что объем передаваемой информации тоже растет.
Если раньше мы смотрели фильмы невысокого качества, умещающиеся на одной болванке, то сейчас фильмы качества HD могут занимать десятки гигабайт. Разумеется, для хранения, и тем более передачи, информации такого объема понадобится много места и времени. Именно для таких случаев и используют метод сжатия данных. В нашей статье мы попытаемся понять, как работает сжатие данных без потерь, и рассмотрим самый распространенный метод сжатия без потерь — алгоритм Хаффмана.
Андрей Аксенов «Магия сжатия»
Ключевые слова: данные, информация, сжатие данных, алгоритм Хаффмана, сжатие данных без потерь.
Сжатие данных — это алгоритмический процесс уменьшения объема данных путем сокращения их избыточности. Сжатие файла — это его уменьшение при сохранении исходных данных. [1] Существует два метода сжатия: с потерями и без потерь. При сжатии с потерями восстановленные данные несколько отличаются от исходных, например: разрешением, качеством звука и т. д..
Используют этот метод при сжатии изображений, аудио и медиа файлов, когда нет необходимости точного восстановления данных. При сжатии без потерь исходные данные восстанавливаются с точностью до бита. Такой способ используют для хранения и передачи текстовых документов, компьютерных программ. Далее мы будем рассматривать именно второй способ. [2]
Сжатие без потерь (СБП) уменьшает биты путем выявления и устранения статистической избыточности. Рассмотрим следующий пример, чтобы понять принцип работы этого метода. [4] На рисунке ниже изображено девять овалов- три бордовых, три зелёных, три желтых:

Вместо того, чтобы показывать все девять овалов, мы можем убрать все овалы, оставив по одному овалу разного цвета, и указав на них цифрами сколько было этих овалов вначале. То есть мы показываем те же данные, но используя меньшее количество фигур:

Оба рисунка несут в себе один и тот же смысл, содержат одну информацию, но на втором рисунке информация сжата, при хранении и передаче занимает меньше места.
Сжатие данных. Пример на python
Другой пример: возьмем файл, который хранит следующую информацию-
DDDDDDDDDDDYYYYYYFFFFFFFFFFFFFFFFFFFOOO. Этот текст мы можем сжать следующим образом: D11Y6F19O3. Таким образом вместо 39 символов, мы использовали 11 для представления тех же данных.
На первый взгляд, принцип сжатия данных выглядит слишком идеально, чтобы быть правдивым. Идея сокращения информации без потери ее части смотрится как бесплатное предложение, которое должно бы нарушить один малоизвестный закон Ньютона: закон сохранения данных.
Несмотря на окружающую мистическую ауру, сжатие данных основано на простой идее: отображение представления данных из одной группы символов на другую, более компактную серию символов. Чтобы достигнуть этого, программы сжатия данных и соответствующая аппаратура используют несколько различных алгоритмов, самыми основными из которых являются метод Хаффмана и LZW- кодирование. [6]
Простота и легкость данного способа сжатия информации сделали его популярным среди пользователей. Хотя он и был создан в далеком 1952 году, но даже в наше время этот метод остается актуальным. Кодирование Хаффмана работает на принципе того, что есть вероятность, что некоторые символы в представлении данных используются чаще, чем другие. Суть алгоритма в том, чтобы найти символы с большей частотой и дать им самый короткий код, а символам с наименьшей частотой дать самый длинный код. На входе в алгоритме Хаффмана должна быть уже задана таблица частот, без нее кодирование невозможно. [2]
- Задается таблица частот;
- Выбираются два узла с наименьшим весом (частотой);
- Создается родитель равный весу их суммы;
- Родитель — это новый свободный узел, а те два узла-потомка удаляются;
- Для дуги, выходящей из родителя, ставится в соответствие бит 1 или 0;
- Вся эта операция повторяется, пока в списке не останется единственный узел.
Приведем пример. Нам задана следующая таблица частот:
Источник: moluch.ru
Алгоритмы используемые при сжатии данных

Одна из самых главных проблем при работе с данными — это их размер. Нам всегда хочется, что бы уместилось как можно больше. Но иногда этого не сделать. Поэтому нам на помощь приходят различные архиваторы. Но как они сжимают данные?
Я не буду писать о принципе их работы, лишь расскажу о нескольких алгоритмах сжатия, которые они используют.
Алгоритм Хаффмана
Коды или Алгоритм Хаффмана (Huffman codes) — широко распространенный и очень эффективный метод сжатия данных, который, в зависимости от характеристик этих данных, обычно позволяет сэкономить от 20% до 90% объема.
Рассматриваются данные, представляющие собой последовательность символов. В жадном алгоритме Хаффмана используется таблица, содержащая частоты появления тех или иных символов. С помощью этой таблицы определяется оптимальное представление каждого символа в виде бинарной строки.
Построение кода
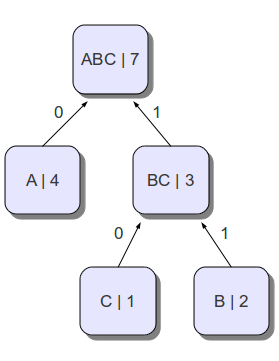
- a b c
- 4 2 1
Обрабатываем b и c

- a b c
- 0 11 10
Получившееся дерево
Преобразование MTF
Преобразование MTF (move-to-front, движение к началу) — алгоритм кодирования, используемый для предварительной обработки данных (обычно потока байтов) перед сжатием, разработанный для улучшения производительности последующего кодирования.
Построение кода
- Символ Список Вывод
- B ABC 1
- C BAC 2
- A CBA 2
- B ACB 2
- A BAC 1
- A ABC 0
- A ABC 0
Обратное преобразование
- Символ Список Вывод
- 1 ABC B
- 2 BAC C
- 2 CBA A
- 2 ACB B
- 1 BAC A
- 0 ABC A
- 0 ABC A
Преобразование Барроуза-Уиллера
Преобразование Барроуза — Уилера (Burrows-Wheeler transform, BWT) — это алгоритм, используемый в техниках сжатия данных для преобразования исходных данных.
Bzip2 использует преобразование Барроуза-Уилера для превращения последовательностей многократно чередующихся символов в строки одинаковых символов, затем применяет преобразование MTF, и в конце кодирование Хаффмана.
Работа алгоритма

Преобразование выполняется в три этапа. На первом этапе составляется таблица всех циклических сдвигов входной строки. На втором этапе производится лексикографическая (в алфавитном порядке) сортировка строк таблицы. На третьем этапе в качестве выходной строки выбирается последний столбец таблицы преобразования. Следующий пример иллюстрирует описанный алгоритм:
Пусть нам дана исходная строка s=«ABACABA».
Результат вкратце запишем так: BWT(s)=(«BCABAAA», 3), где 3 — это номер исходной строки в отсортированной матрице, так как он может понадобиться для обратного преобразования.
Следует заметить, что иногда в исходной строке приводится так называемый символ конца строки $, который в преобразовании будет считаться последним символом, тогда сохранение номера исходной строки не требуется. При аналогичном вышеприведённом преобразовании та строчка в матрице, которая будет заканчиваться на символ конца строки и будет исходной («ABACABA$»). При этом при сортировке матрицы данный символ будет рассматриваться как самый последний после всех символов алфавита. Тогда результат можно записать так BWT(s)=»$CBBAAAA». Он будет эквивалентен первому, так как также содержит все символы исходной строки.
Обратное преобразование

Пусть нам дано: BWT(s)=(«BCABAAA», 3). Тогда выпишем в столбик нашу преобразованную последовательность символов «BCABAAA». Запишем её как последний столбик предыдущей матрицы (при прямом преобразовании Барроуза — Уилера), при этом все предыдущие столбцы оставляем пустыми. Далее построчно отсортируем матрицу, затем в предыдущий столбец запишем «BCABAAA». Опять построчно отсортируем матрицу.
Продолжая таким образом, можно восстановить полный список всех циклических перестановок строки, которую нам надо найти. Выстроив полный отсортированный список перестановок, выберем строку с номером, который нам был изначально дан. В итоге мы получим искомую строку. Алгоритм обратного преобразования описан в таблице ниже:
Следует также заметить, что если нам было бы дано BWT(s)=»$CBBAAAA», то мы также получили бы нашу исходную строку, только с символом конца строки $ на конце: ABACABA$.
Заключение
Эти три алгоритма используются в наше время в утилите bzip2 для сжатия данных. Но и не только, поскольку данные алгоритмы являются очень эффективными в своей работе.
Источник: habr.com