Первое представление о десятичной системе счисления у учеников закладывают в концентре «Сотня» Эта тема в разных программах изучается по-разному.
По программам М.И. Моро и Н.Б.Истоминой нумерацию двузначных чисел начинают изучать в 1-ом классе.
Рассмотрим каждую программу по отдельности.
М1М
Выделяют 2 ступени:
1 ступень (1 класс) – числа от 11 до 20;
2 ступень (2 класс) – числа от 21 до 100.
Эти 2 ступени выделяют потому что:
а) есть разница в названии чисел 1-ой и 2-ой ступени (например, тринадцать — сначала называют единицы, затем десятки; тридцать один – наоборот, сначала десятки, а потом единицы).
б) числа > 20, как говорят, так и пишут (например, 25), а числа до 20 наоборот (14).
Сначала изучают числа 1-ой ступени от 11 до 20.
М1И
Зима! Холода! Песня ЕвгенаБро (Анимация)
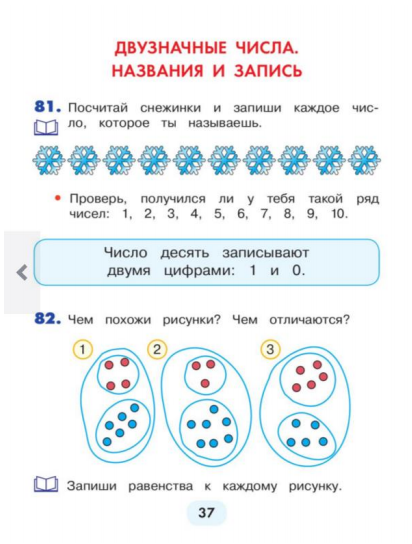
По программе Н.Б.Истоминой, знакомство начинается с числа 10, практическим методом учащиеся узнают сколько единиц в одном десятке, рассматриваются варианты его образования. Вводят понятие «Десяток» и учат считать десятками (стр. 39). А также десятками и единицами вместе (стр. 41).
Изучение двузначных чисел по программам М.И. Моро и Н.Б.Истоминой. проходит в 4 этапа:
I. Подготовительный этап
II. Изучение устной нумерации
III. Изучение письменной нумерации
I. Подготовительный этап. (до начала изучения темы за 2-3 урока)
1) повторить числа от 1 до 10;
2) познакомить с различными счетными единицами;
3) проверить, что дети знают о числах от 11 до 20.
Для реализации первой цели на устном счёте можно предложить различные варианты упражнений:
1. Обратный и прямой счёт в пределах первого десятка, через 1,2,3. Можно предложить посчитать что-то в классе (количество окон, ламп, шкафов и тд)
2. Сравнение чисел
-на основе сравнения групп предметов.
— по месту числа в натуральном ряду чисел
3. Числовые лесенки.
4. Работа с числовым рядом:
-назови следующее число за числом…
-назови предыдущее число…
-назови «соседей» числа…
-какое число стоит между числами.
5. Присчитывание и отсчитывание по 1.
Присчитать 1, т.е. назвать следующее число за данным.
Отсчитать 1, т.е. назвать предыдущее число.
В соответствии с 3-ей целью выясним: умеют ли дети считать с выходом за десяток, даем задания на сравнение. Пример: какое число стоит после числа 6, а после 16?
Данных заданий в учебниках М.И. Моро и Н.Б. Истоминой нет этих упражнений перед изучением нумерации двузначных чисел, поэтому учитель сам дает эти задания, используя различный методический и наглядный материал, интерактивные задания и тд.
лучший учебник по математике (начальная школа), ошибки начальной школы в математике — Л. А. Ясюкова
II. Изучение устной нумерации.
УМК «Школа России» М.И. Моро
Цель: 1) Объяснить 2 способа образования чисел от 11 до 20;
2) Показать, как образуются названия чисел от 11 до 20;
3) Показать последовательность чисел от 11 до 20 и провести работу по ее заучиванию;
4) Рассмотреть десятичный состав чисел от 11 до 20.
На 1 уроке сначала детей знакомят с новой счетной единицей – десятком.
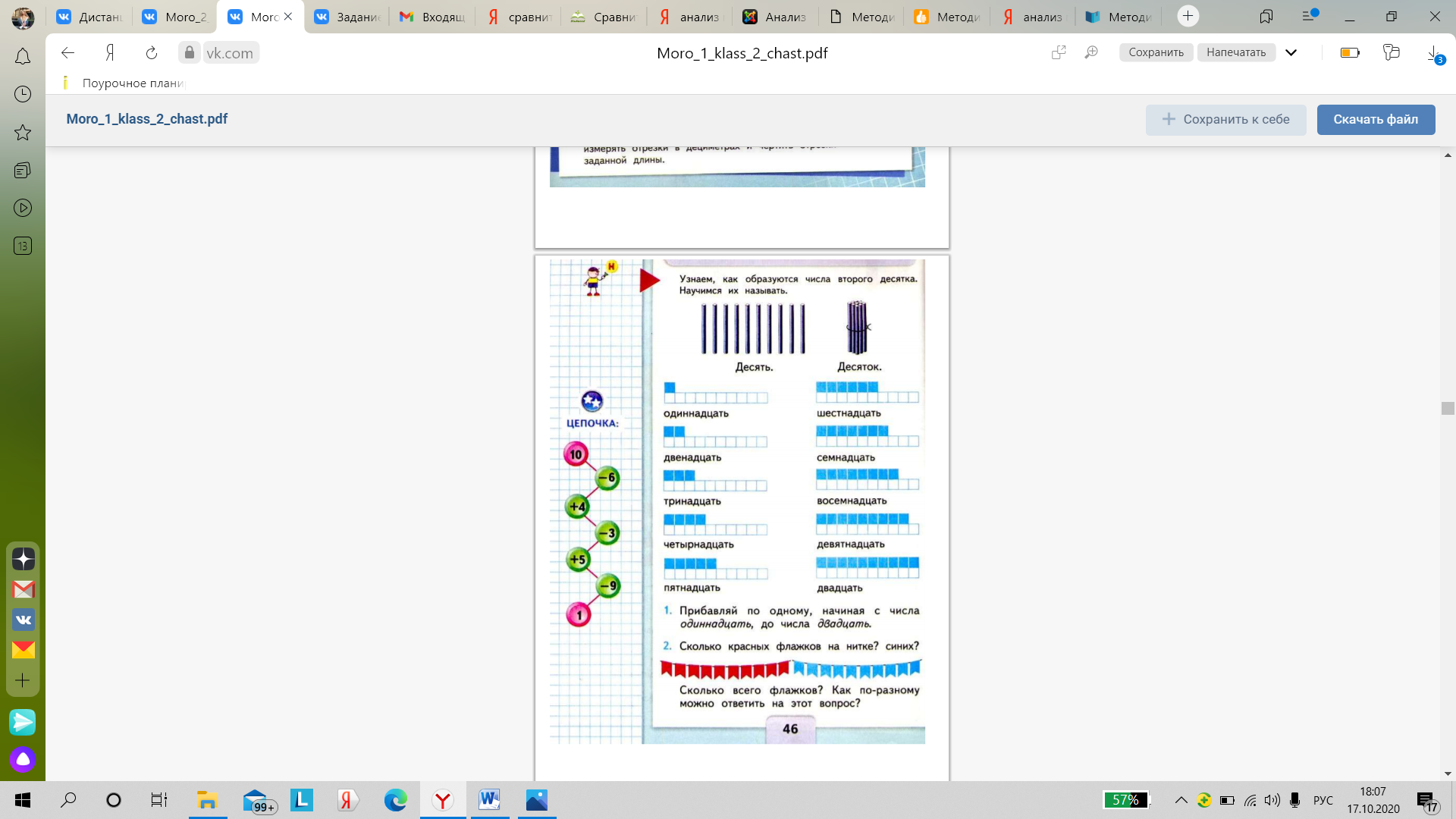
Стр. 46. М1М ч.2
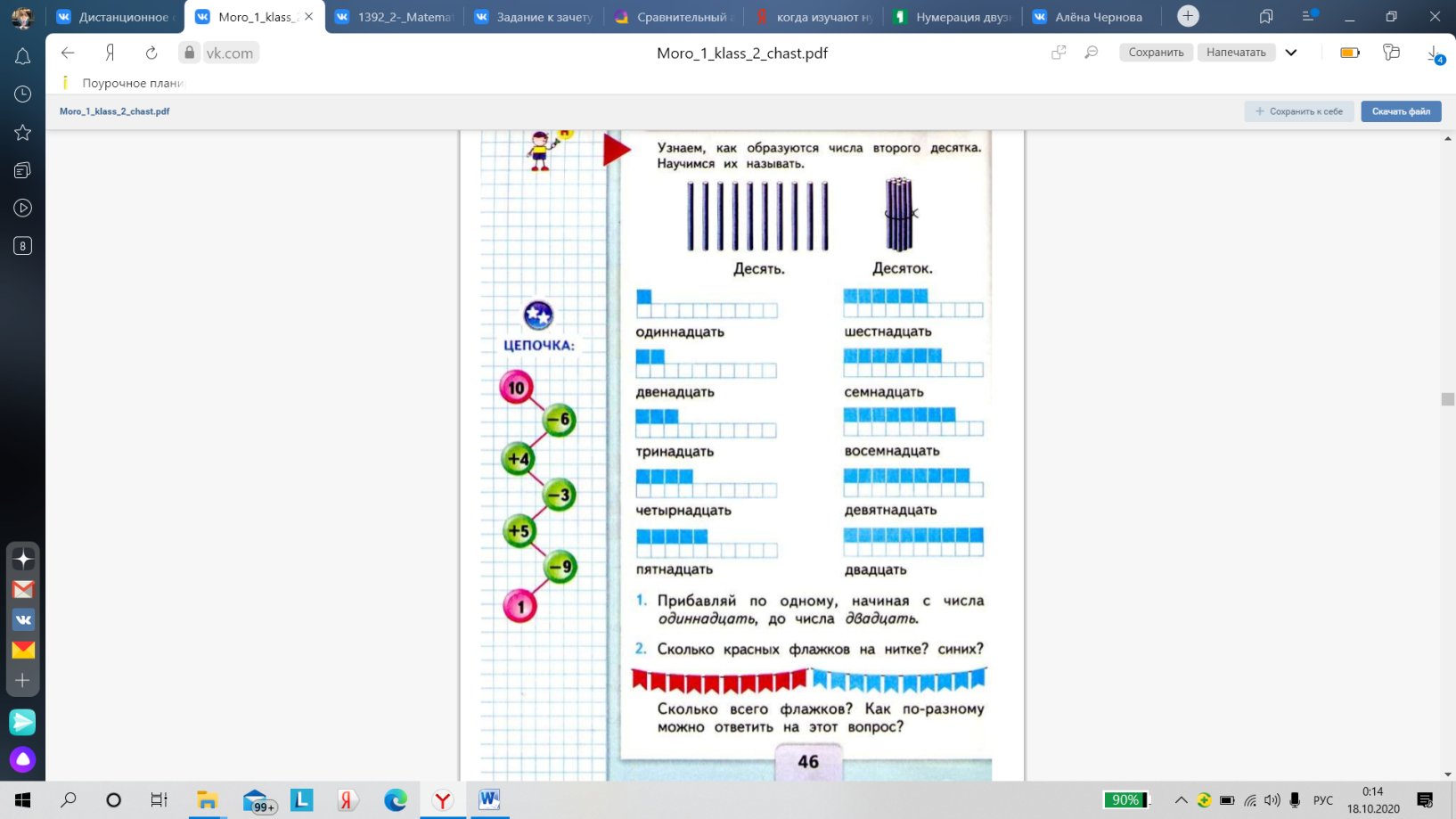
10 палочек это десяток. Десятками тоже можно считать как простыми единицами: 1 десяток, 2 десятка, 3 десятка…
После этого по программе Моро вводим числа от 11 до 20. Вспомним, как образуются числа от 1 до 10. Ответ ученика: чтобы получить следующее число, надо к данному числу прибавить единицу.
Этим же способом будем образовывать числа после 10.
На столе 10 палочек или 1 десяток. К одному десятку (пучку) добавим сверху 1 единицу.
В старые времена 10 заменяли словом «дцать». Получаем:
Один-на-дцать (устаревшее) на доске
Это новое число состоит из 1 десятка и 1 единицы.
Давайте образуем следующее число, для этого к данному числу добавим 1 и того на 1-м десятке лежит 2 палочки, получили две- на- дцать или двенадцать, это число состоит из 1 десятка и 2х единиц. Так же подробно разбирают 13, 14,15,16,17,18,19.
Отдельно разбирают 20. Когда к 19+1, получили 2 пучка – десятка или двадцать.
Показываем, что 20 состоит из 2 десятков, т.е. два-дцать.
Таким образом, каждое число можно получить 2-мя способами:
1) к предыдущему числу + 1 (способ основан на принципе построения натуральной последовательности чисел);
2) к десятку + несколько единиц (способ основан на разрядном составе числа).
Далее предлагаем упражнения направленные на:
1) закрепление натуральной последовательности чисел до 20:
а) счет (прямой, обратный);
б) назови «соседей» этого числа;
в) какое число стоит между этими числами;
г) назови предшествующее число;
д) назови последующее число;
е) сравни 2 числа по их месту в натуральном ряду и т.д.
2) на закрепление десятичного состава чисел: это различные упражнения с моделями чисел, моделируем на палочках или на «полосках» и «квадратах».
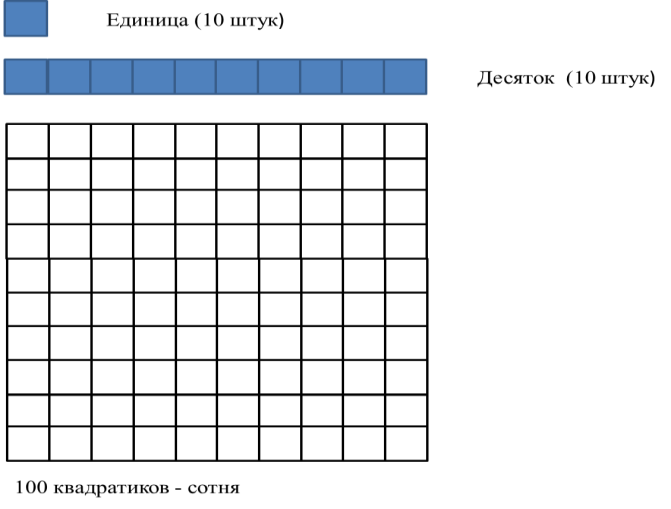
М1М ч.2Стр. 46
Представлены задания типа:
а) составь модель числа 16 (это 1
полоска и 6 квадратиков);
б) выбери модель соответствующую числу 16 (даем несколько моделей, надо выбрать верную модель и доказать);
в) закончи модель (даем начало модели, надо продолжить и доказать);
г) исправь ошибку в модели;
Работа с моделями сопровождается вопросом «сколько в числе десятков и сколько единиц». Дети отвечают по модели, которую они сделали на парте
Так же в этой группе предлагают задания типа:
— сравни числа (по десятичному составу). Пример: какое число больше 16 или 18? (в этих числах по одному десятку, но в 1-ом числе 6 единиц, а во 2-ом – 8, 616)
III. Изучение письменнойнумерации чисел. М1М ч.2 стр. 50
Цель: познакомить с записью чисел от 11 до 20 и принципом поместного значения цифры в числе (ППЗЦТ).
Используют абак с двумя рядами карманов:
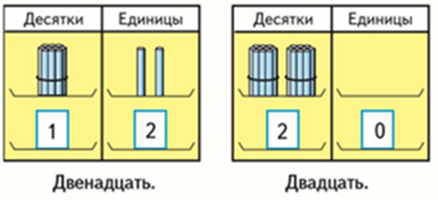
Сегодня мы научимся записывать числа от 11 до 20. Давайте, например, запишем число 12. Сколько в этом числе десятков и единиц (1дес и 2 ед). Поставим в верхний ряд карманов один пучок и две палочки. Обозначим количество единиц и десятков цифрами. Слева в нижнем ряду ставим цифру 1, т.к. здесь один десяток, а справа цифру 2, т.к. 2 палочки. Получим запись числа 12.
Потребовалось 2 цифры, обсуждаем какие это цифры и что они обозначают.
Аналогично разберем запись других чисел (на абаке).
Отдельно разбираем число 20. В нем только 2 десятка и 0 отдельных единиц.
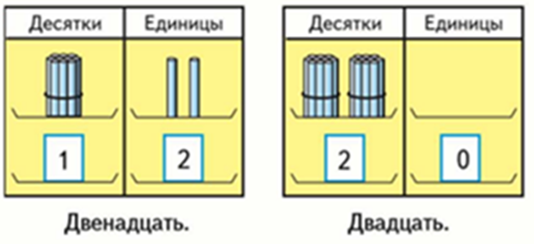
После этого можно ввести понятие однозначные и двузначные числа.
Затем идет закрепление устной и письменной нумерации, для чего включают упражнения 3-х групп:
1 группа – закрепление натуральной последовательности (упражнения такие же, как и на 1-ом этапе).
1. Запишите ряд чисел от 1 до 20 или от 5 до 15, или от 20 до 10 и т.д.
2. Расставь числа по порядку и запиши полученный ряд чисел.
3. Запиши соседей числа 12
Смотри упражнения 1-ой группы на этапе устной нумерации.
2 группа – упражнения на закрепление десятичного состава чисел:
1. Запиши число, в котором 1 десяток и 2 единицы.
2. Запиши число в виде суммы разрядных слагаемых (или в виде суммы десятков и единиц) 12=10+5
4. Работа с моделями
· Представлено несколько моделей чисел (или на палочках или на полосках и квадратах). Нужно:
a) Выбрать правильную модель числа;
b) Найти ошибку в модели числа;
c) Закончи модель числа;
d) Установи соответствие между несколькими числами и моделями, соедини их стрелками.
5. Сравнение чисел на основе разрядного состава. Сравни 17 и 18. 17-это1 десяток 7 единиц; 18-это 1 десяток 8 единиц, значит 17 меньше 18.
IV этап. Обобщение.
Используют упражнения 3-х групп (см. выше) + задание «Расскажи, что ты знаешь об этом числе».
УМК «Гармония» Н.Б.Истомина
Цель: 1) Объяснить 2 способа образования чисел от 11 до 20;
2) Рассмотреть разрядный состав чисел от 11 до 20.
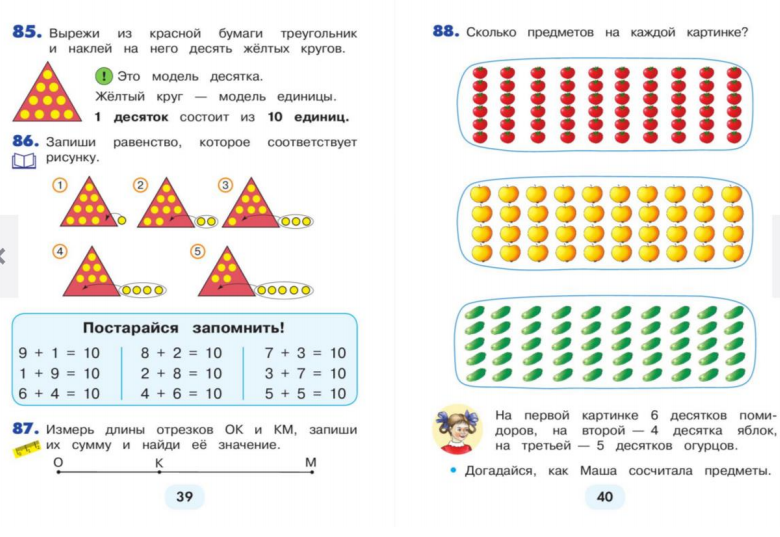
По программе Н.Б.Истоминой сначала вводится понятие десяток. 10 единиц(желтых кружков) это десяток. Десятками тоже можно считать как простыми единицами: 1 десяток, 2 десятка, 3 десятка

Перед изучением устной нумерации школьники учатся моделировать числа с помощью — десятки и — единицы (стр. 41-42).

Моделируем неразрядные числа, состоящие из десятков и единиц, и учимся их записывать (стр. 42). Задание 90. Давайте запишем цифрами число, которое соответствует рисунку.
Учатся записывать числа, опираясь на рисунок.
Только после этого вводят название чисел (стр. 43). Особое внимание уделяется таким числам, как сорок и девяносто. Затем идет сравнение однозначного числа и двузначного, с таким количеством десятков.
-Чем отличаются числа в каждой паре (1 и 10, 2 и 20, 6 и 60)

Таким образом, в этом учебнике поэтапность знакомства с двузначными числами отличается от УМК «Школа России», сначала детей знакомят с письменной нумерацией, затем с устной. До тех пор пока не введена устная нумерация, говорят так, например, 4 десятка и 2 единицы — 42.
Отдельно разбирают числа от 11 до20 (с.46)
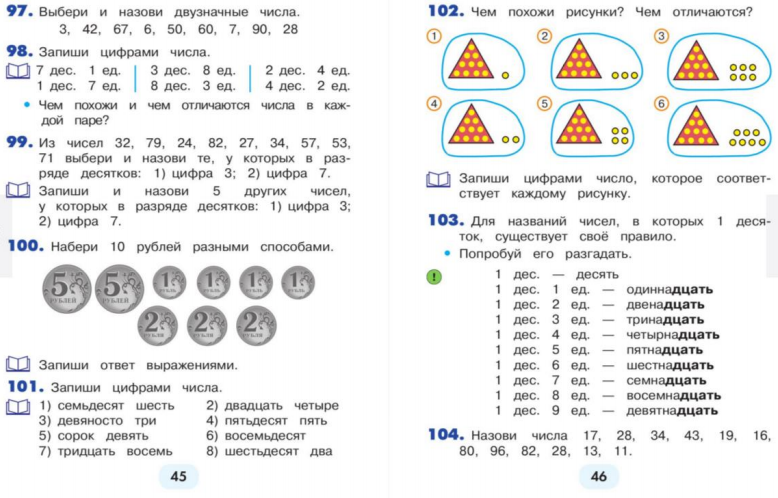
Для закрепления письменной нумерации используют задания 3-х групп.
М1М ч.2 стр.56 М1И ч.2 стр. 47

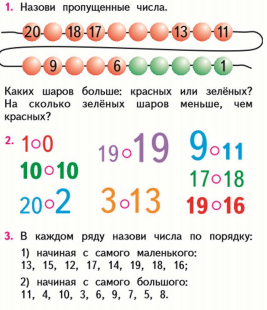
IV этап. Обобщение.
Используют упражнения 3-х групп (см. выше) + задание «Расскажи, что ты знаешь об этом числе».
Числа от 21 до 100 по программе Н.Б.Истоминой изучаются в первом классе и не выделяются в отдельную группу, а во втором классе дается больше заданий на работу с двузначными числами.
Значит, подготовительного этапа, этапа изучения устной нумерации от 21 до 100 и этапа письменной нумерации как таковых нет, во втором классе идем закрепление изученного.
В учебнике нет явного знакомства с понятиями «однозначные и двузначные числа» и «сумма разрядных слагаемых»
Рассмотрим какие упражнения даются на закрепление двузначных чисел во втором классе.
Для закрепления письменной нумерации используют задания 3-х групп.
– на закрепление натуральной последовательности чисел.

– на закрепление принципа записи чисел.
1) Какие цифры использованы для записи данного числа? Что они обозначают?
2) Сравни записи чисел 45 и 54.Чем похожи, чем отличаются?
3) Используя цифры о, 5, 9 запиши все возможные двузначные числа.

IV этап. Обобщение.
Используют упражнения разного типа (см. выше) + задание «Расскажи, что ты знаешь об этом числе».
ВЫВОД:
Уроки математики должны быть нацелены на формирование у детей зачатков научного мировоззрения. Этому способствует укрепление связи обучения с жизнью, с практикой.
В учебниках математики программ «Школа России» и «Гармония» изучение двузначных чисел в пределах 100 представлено интересно и понятно для ребенка. Структура практического материала построена последовательно, но этапы изучения различаются.
В отличии от учебника М.И. Моро, Н.Б. Истомина не разделят знакомство с двузначными числами на ступени, что по моему мнению, труднее для детей, так как они сразу начинают работать с большими числами, а не поэтапно.
Задание №1
Сравнительный анализ методических подходов к изучению нумерации двузначных чисел, предложенных в альтернативных учебниках математики М.И. Моро (школа России) и др. и Н.Б. Истоминой
Первое представление о десятичной системе счисления у учеников закладывают в концентре «Сотня» Эта тема в разных программах изучается по-разному.
По программам М.И. Моро и Н.Б.Истоминой нумерацию двузначных чисел начинают изучать в 1-ом классе.
Рассмотрим каждую программу по отдельности.
М1М
Выделяют 2 ступени:
1 ступень (1 класс) – числа от 11 до 20;
2 ступень (2 класс) – числа от 21 до 100.
Эти 2 ступени выделяют потому что:
а) есть разница в названии чисел 1-ой и 2-ой ступени (например, тринадцать — сначала называют единицы, затем десятки; тридцать один – наоборот, сначала десятки, а потом единицы).
б) числа > 20, как говорят, так и пишут (например, 25), а числа до 20 наоборот (14).
Источник: infopedia.su
ПРОГРАММА МОРО и ИСТОМИНА
Подготовка младших школьников к введению типовых задач с пропорциональными величинами. Формирование у учащихся первых представлений о пропорциональной зависимости величин. Какие методические приемы может использовать учитель с этой целью? Проанализируйте альтернативные учебники математики для начальных классов и приведите примеры различных упражнений, используемых для ознакомления учащихся с тройками величин и зависимостями между ними. Какой методический подход вам показался наиболее интересным и почему?
Все составные задачи в курсе математики начальных классов можно условно поделить на две группы.
Составные задачи
| Типовые | Нетиповые |
| -На нахождение четвертого пропорционального -На пропорциональное деление или на нахождение неизвестного по двум суммам -На нахождение неизвестного по двум разностям -На движение | Все остальные задачи, которые не подходят ни под один из типов, называют нетиповыми. Их классифицируют по видам простых задач, входящих в них. |
При решении типовых задач учащиеся знакомятся с тройками пропорциональных величин. Их решение позволяет осуществлять пропедевтику понятий «прямая и обратная пропорциональная зависимость», которые будут изучаться в средней школе.
В начальных классах такая терминология не вводиться, мы говорим лишь о тройках пропорциональных величин, учим детей выделять их в задаче и разбираем, как эти величины взаимосвязаны.
В каждой из троек величин выделяют:
1) единицу – т.е. величину, которая повторяется несколько раз;
2) количество повторений единицы;
3) общее значение величины.
Детей знакомят с такими основными тройками, как:
• Цена – количество – стоимость;
• Масса одного предмета – количество предметов – общая масса;
• Емкость (объем) одного сосуда – количество сосудов – общая емкость (объем);
• Расход ткани на 1 вещь – количество вещей – общий расход ткани;
• Выработка в единицу времени (производительность) – время работы – общая выработка;
• Скорость – время – расстояние;
• Длина – ширина – площадь
Кроме этих троек величин в задачах встречаются и другие. Например:
Количество клубков на 1 свитер – количество свитеров – общее количество клубков.
С этими тройками величин учащиеся начинают знакомиться в 3 классе при изучении темы «умножение и деление».
Взаимосвязи между величинами в тройке отражается в трех видах простых задач:
1. Нахождение общей величины (умножение);
2. Нахождение единицы (деление);
3. Нахождение количества (деление).
На подготовительном этапе в 3 классе учащихся начинают знакомить с этими тройками величин. Обычно в качестве первой берут тройку «цена – количество – стоимость». Организуют дидактическую игру «в магазин» (канцелярский). Учитель выставляет у доски «товар» и на каждый предмет прикрепляет ценник. Разыгрывают ситуации, в процессе которых вводят понятие «цена» — стоимость одного товара, «количество» — сколько предметов купили, «стоимость» — сколько денег заплатили.
Составляем тройки взаимообратных задач и учимся их записывать кратко в таблицу.
| Цена | Количество | Стоимость |
| 2 р. | 4 шт. | ? |
| ? | 4 шт. | 8 р. |
| 2 р. | ? | 8 р. |
Таким же образом вводят и другие тройки величин на других уроках (1 тройка величин -1 урок).
При введении лучше использовать практическую работу.
На подготовительном этапе учащиеся должны научиться решать простые задачи с тройками величии разного рода.
Позднее из этих простых задач составляют составные нетиповые задачи в два действия. Например: Мама купила 3 пакета муки по 2 килограмма в каждом и 1 кг яблок. Какова масса всей покупки?
Эту задачу можно разделить на 2 простых.
1 задача – на нахождение общей массы муки с тройкой величин.
2 задача – на нахождение суммы двух величин.

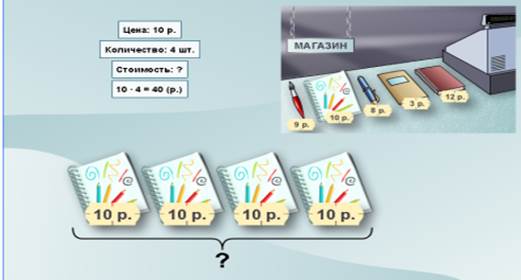
ПРОГРАММА МОРО и ИСТОМИНА
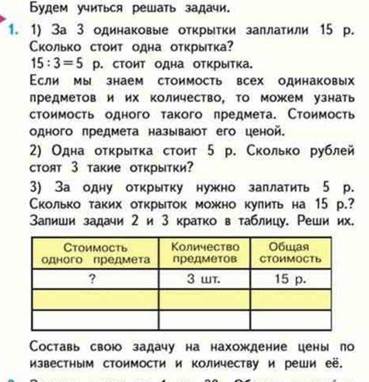
М3И ч2 стр 40-41
Масса одного предмета-количество предметов-общая масса
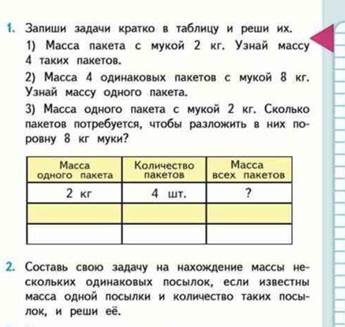
Емкость (объем) одного сосуда – количество сосудов – общая емкость (объем);
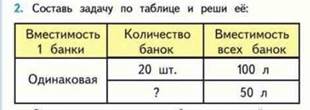
• Расход ткани на 1 вещь – количество вещей – общий расход ткани;
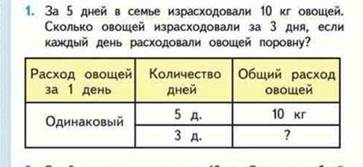
• Выработка в единицу времени (производительность) – время работы – общая выработка;

М3Мч2 стр 17 номер 4
• Скорость – время – расстояние;
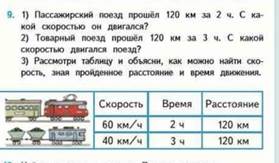
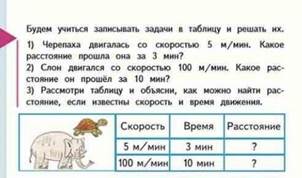
• Длина – ширина – площадь
Сделайте сравнительный анализ альтернативных учебников математики (программы М.И.Моро и Н.Б.Истоминой) и выясните, с какими видами задач на нахождение 4-го пропорционального знакомят учащихся начальных классов по различным программам. Какова последовательность их введения? Когда они появляются в учебнике впервые? Проведите анализ учебников по двум программам. Для выбранных задач составьте таблицы.
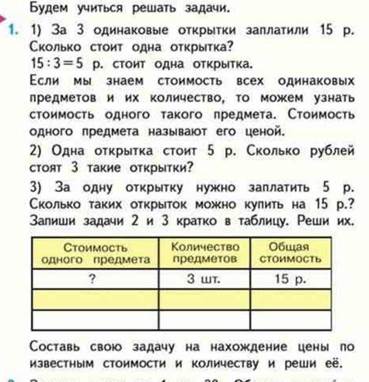
| Цена | Количество | Стоимость | |
| 1 откр 2 откр | одинаковая | 3 шт 1 шт | 15 р ? |

М3Мч1 стр 61 номер 7
| Расход ткани на 1 м | Количество вещей | Общий расход ткани |
| одинаковое | 8 шт ? | 24 м 15 м |
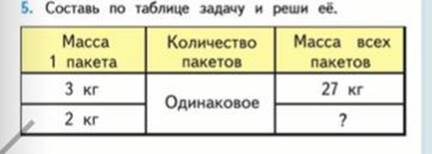

М4Мч1 стр 87
| Расход ткани на 1 м | Количество вещей | Общий расход ткани | |
| Детские платья Взрослые платья | 2 м ? | 32 шт 16 шт | одинаковый |
Методика их изучения по программе Моро М.И. такая: каждый вид вводят по очереди в три этапа: подготовка, ознакомление и формирование умения решать такие задачи.
Но анализ учебников показывает, что не все 6 видов есть в учебнике. Есть специальные уроки для введения 1 и 2 видов (М4М ч.1 с.86), можно найти задачи 3 и 4 видов. Хотя их введение специальными уроками в учебнике не предусмотрено. Нет задач 5 и 6 видов, следовательно, учитель сам продумывает тематический план их введения и, если класс сильный, можно рассмотреть все 6 видов, если слабый, то первые 4 вида. Решаем эти задачи с различными тройками величин.
Проанализируйте учебники математики для начальных классов по программам М.И.Моро и Н.Б.Истоминой и приведите примеры различных видов типовых задач на нахождение неизвестного по двум суммам (на пропорциональное деление) и по двум разностям. Какова последовательность введения различных видов этих задач в учебниках М.И. Моро, И.И. и Н.Б. Истоминой.
Когда они появляются в учебнике впервые? Для выбранных задач составьте таблицы.
Задания на нахождение неизвестного по двум суммам

| Цена | Количество | Стоимость |
| 1 кусок 2 кусок | одинаковая | 5 м 4 м |

| Масса одного предмета | Количество предметов | Общая масса |
| 1 мешок 2 мешок | ? Одинаковая ? | 56 кг 24 кг |
Задание на нахождение неизвестного по двум разностям
| Расход ткани на 1 вещь | Количество вещей | Общий расход ткани | |
| 1 кусок 2 кусок | Одинаково | ? ? на 2 больше | 6 м 10 м |
| Масса одного предмета | Количество предметов | Общая масса | |
| 1 столовая 2 столовая | Одинаковая | 5 шт 2 шт | ? на 24 кг больше ? |
Методика работы с задачами этого типа, такая же, как и с задачами предыдущего типа, т.е. все виды вводят по очереди и отрабатывают на различных тройках величин, но анализ учебников по программе М.И.Моро 4 класс показывает, что эта схема выполняется не полностью. Есть специальные уроки, где вводят задачи 1 и 2 видов (М4М ч.2 с. 46), а введение остальных видов не предусмотрено. Но учитель может предусмотреть это сам. Для сильного класса возможно введение 6 видов, а для слабого достаточно 2 видов.
Источник: poisk-ru.ru
Анализ учебников по программам «Школа России» Моро М.И и «Школа 2000» Петерсон Л.Г.;
«Методика обучения решению задач на нахождение четвертого пропорционального».
Студентка 5 курса ЗНО-116
Заочного отделения кафедры ППДНО
Кожухова Ирина Павловна
к. п. д. доцент кафедры ППДНО
Болотова Татьяна Владимировна
Владимир 2020 г
С какими видами задач на нахождение 4-го пропорционального знакомят учащихся начальных классов поразличным программам. Какова последовательность их введения? Укажите страницы учебников математики, на которых они впервые появляются. Приведите тексты этих задач. Сделайте сравнительный анализ альтернативных учебников математики по программам Моро М. И и Петерсон Л. Г.;
Начальное образование — это важный период обучения в школе, в котором закладывается основа мотивационной и учебной деятельности. Учебный багаж, полученный на первом году обучения, является фундаментом всего дальнейшего обучения. Приобретённые знания помогут ребятам в дальнейшем осознанно принимать решения в жизни и нести за них ответственность.
В учебно-методических комплексах начальной школы текстовые задачи занимают большой объем заданий. Они необходимы, чтобы обучающиеся легко ориентировались в обыденной жизни среди различных величин и использовали свои умения при решении возникающих проблем. Чтобы решить проблему, необходимо понять её суть и сформулировать вопрос. В связи с этим необходимо обучающихся с первого класса учить формулировать задачу. Как заметили современные педагоги и исследователи, в школе уделяют внимание решению готовых задач, а вот составлять новые задачи и преобразовывать имеющиеся, школьники практически не умеют.
Текстовые задачи можно классифицировать на задачи:
· с пропорциональными величинами (движение (скорость, время, расстояние);
· работа (производительность, время, объем работы);
· стоимость (цена, количество, стоимость);
· расход материала (расход на 1 предмет, количество предметов, общий расход);
· сбор урожая (урожайность, масса урожая, площадь участка) и т. п. );
· задачи на нахождение четвертого пропорционального;
· на пропорциональное деление;
· на нахождение неизвестных по двум разностям;
· задачи логического и комбинаторного характера;
· на нахождение доли целого и целого по его доли.
Многочисленный анализ педагогической литературы показывает, что работа над задачей состоит из нескольких этапов, которые необходимо учитывать при обучении школьников решению различных задач, в частности задач на нахождение четвертого пропорционального. В задачах на нахождение четвертого пропорционального даются три величины, связанные пропорциональной зависимостью (прямой, обратной) и необходимо найти четвертую — искомую величину. Четыре величины составляют пропорцию, из чего и следует название этого типа задач. Величинами в этих задачах могут быть: цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и другие.
Рассмотрим методику обучения решению задач на нахождение четвертого пропорционального на следующем примере.
Задача. Мама купила несколько пирожков с капустой по 16 рублей за штуку и столько же пирожков с мясом по 32 рубля за штуку. За пирожки с капустой она заплатила 96 рублей. Сколько она заплатила за пирожки с мясом?
Первый этап работы учителя с учениками относится к подготовительной работе, которая предусматривает знакомство детей с величинами: цена, количество, стоимость и другими пропорциональными величинами и связями между ними.
1. О чем задача? (Задача о покупке двух видов пирожков. Покупка характеризуется ценой за одну единицу товара, количеством и общей стоимостью).
2. Что необходимо найти? (В задаче необходимо найти общую стоимость пирожков).
3. Что означает фраза «столько же»? (В задаче указывается два вида пирожков, и они имеют одинаковое количество, а значит, если будет вычислено количество пирожков с капустой, то будет известно количество пирожков с мясом).
4. Что известно о каждом виде пирожков? (В задаче известно, что: а) стоимость одной штуки каждого вида пирожков — 16 рублей стоит пирожок с капустой и 32 рубля пирожок с мясом; б) общая стоимость всех пирожков с капустой — 96 рублей).
5. Что неизвестно? (В задаче неизвестно количество купленных пирожков с капустой и мясом).
6. Что является искомым? (Количество пирожков с мясом и капустой, стоимость пирожков с мясом).
Третий этап предполагает анализ текста задачи. Анализ направлен на её осмысление. При решении данной задачи составляется таблица, в которую вносятся условия задачи (таблица 1).
Таблица 1. Условие задачи
После того, как составлена схема и разобрали условие, школьникам предлагают ответить на несколько вопросов:
· можно ли сразу ответить на главный вопрос задачи?
· какое действие необходимо выполнить вначале?
· какое математическое действие необходимо выполнить, чтобы найти необходимую величину?
Четвертый этап подразумевает запись решения.
1. 96: 16 = 6 (шт. ) — количество пирожков с капустой и мясом.
2. 32*6 = 192 (р. ) — сумма, потраченная на покупку пирожков с мясом.
Ответ: 192 р. стоили пирожки с мясом.
Пятый этап — проверка правильности решения.
Последним этапом над работой с задачей является самопроверка. Самопроверка позволяет проверить решение задачи на наличие ошибок в ответе. Для начала составим обратную задачу на нахождения другого неизвестного числа.
Задача. Мама купила несколько пирожков с капустой по 16 рублей за штуку и столько же пирожков с мясом. За пирожки с капустой она заплатила 96 рублей, а за пирожки с мясом 192 рубля. Сколько стоил один пирожок с мясом? При решении обратной задачи составляется таблица, в которую вносятся условия (таблица 2).
Таблица 2. Условие обратной задачи
1. 96: 16 = 6 (шт. ) — количество пирожков с капустой и мясом.
2. 192: 6 = 32(р. ) — цена одного пирожка с мясом.
Ответ: стоимость одного пирожка с мясом составляет 32 рубля.
Таким образом, видим, что числовые значения с первоначальным вариантом задачи совпадают, соответственно задачу решили правильно.
В результате проведенного анализа можно сделать вывод, что методика обучения решению задач на нахождение четвертого пропорционального не отличается своими этапами от решения простой задачи. Рассмотренная нами методика позволяет повысить мыслительную активность обучающихся, помогают понять условие задачи и осознанно выбрать необходимое математическое действие.
Анализ учебников по программам «Школа России» Моро М. И и «Школа 2000» Петерсон Л. Г.;
В УМК Моро М. И. мы впервые встречаем задачу на нахождение четвёртого пропорционального во 3 классе.

На следующей же странице даётся подробное ообъяснение, как решать задачи подобного типа.

Учащихся обучают составлять таблицы по данным зачам. Это мы наблюдаем на следующих страницах:


В 1 части учбника Моро 3 класса мы видим подготовительный этап обучения решению задач на нахрождение четвертого пропорционального. Для изучения темы нет отдельного параграфа или урока.
После подготовительного этапа на специальном уроке в 3 классе впервые вводят задачи на нахождение четвертого пропорционального. Таких задач может быть 6 видов, в каждом из которых одна величина постоянна (одинаковая), а из 4-х значений двух других величин одно значение из четырех возможных неизвестно (4-е пропорциональное), а остальные 3 известны. Примеры задач всех видов задач даны на следующих слайдах.


1-4 вид отражают прямопропорциональную зависимость. Например, чем больше цена (количество), тем больше стоимость при постоянном количестве (цене). Их вводят в 3 классе.
5 – 6 вид задач на обратнопропорциональную зависимость. Например, чем больше цена, тем меньше количество при постоянной стоимости и наоборот. Их вводят в 4 классе.
Величина при этом могу быть совершенно раличными. Основные представлены в таблице ниже:

1 тип задач на нахождение четвертого пропорционального встречаем в 3 классе в учебнике Моро 2 части на страницу 9:

2 тип задач в 3 классе в цчебнике Моро на странице 45:

3 тип задач в 3 классе в учебнике Моро на 18 странице:

В этом примере младшие школьники должны самостоятельно составить краткую запись задачи в таблице.
1-3 виды задач автор учебников вводит постепенно, но начиная в 4-ого вида этот порядок нарушается. Методика введения нарушается, практически нет специальных теоретических уроков, а самих задач становится недостаточно для отработки задач 4-6 типа на нахождение четвертого пропорционального.
5 вид задач на нахождение четвертого пропорционального видим в 4 классе 1 части учебника Моро на странице 87:

В ней ученики учатся работать с обратнопропорциональной зависимостью. Такие задачи сложнее, потому вводятся по программе Моро только с 4 класса.
Ниже рассмотрим введение задач на нахождение четвертого пропорционального в УМК «Школа 2000» Петерсон Л. Г.
1 и 2 тип задач мы встречаем в 3 класс 1 части учебника математики на странице 19:

Задачам этого типа выделен полноценный урок. Теоретические материалы отсутствуют. Учитель должен самостоятельно донести до младших школьников способы решения задач подобного типа. Однако самих задач представлено в достаточном объёме, чтобы в полной мере отработать способ решения задач на нахождение четвертого пропорционального.
На следующем уроке учащиеся знакомятся с 3 типом задач. Это можно наблюдать в 1 части 3 класса на странице 21 учебника Петерсон:

Важно отметить, что в УМК «Школа 2000
» много внимания уделется повторению изученного материала. Его закрепления. Поэтому через некоторое время учащиеся вновь возвращаются к задачам 1 типа на нахождение четвертого пропорционального. Это можно наблюдать в учебнике Петерсон 3 класса 1 части на странице 30:



На странице 99 этого же учебника учащиеся вспоминают способ решения 3 типа задач.

Задачи 4-6 типов представлены учащимся в 4 классе в 1 части учебника Петерсон на странице 3

И чуть позже на странице 6 этого же учебника