Методы максимизации прибыли при формировании производственной программы предприятия

В микроэкономике принято выделять два главных метода определения максимальной прибыли:

1. совокупный;
2. предельный.

Первый метод подразумевает расчет максимальной прибыли при установленном объеме выпуска, суммарных издержках предприятия и суммарном доходе.

Второй метод подразумевает расчет максимальной прибыли при установленном объеме выпуска, предельных издержках и предельном доходе.

Предельный индикатор обозначает, что показатель рассчитан на дополнительную единицу.

Суммарный индикатор обозначает, что показатель рассчитан в общем суммарном выражении.

Например, все затраты предприятия, связанные с осуществлением деятельности, рассчитываются за период. Например, за год. Общая сумма всех затрат за год будет являться суммарными затратами за выбранный период.

Предельные затраты предприятия рассчитываются как отношение изменения суммарных издержек к изменению объема выпуска за выбранный период. То есть сравниваются полученные затраты до и после того, как объем выпуска изменился.

1.8 Теории фирмы и принцип максимизации прибыли.

Замечание 1

На предприятии могут использоваться оба метода для того, чтобы определить максимальную прибыль и оптимальный объем производства.

Совокупный метод

На схеме 1 приведен пример определения максимизации прибыли совокупным методом. Еще данный метод называется — метод общих доходов и издержек при максимизации прибыли.

Общая прибыль изучаемого предприятия – это всегда разница от совокупной выручки (за выбранный период) и общими издержками (за выбранный период). Формула расчета общей прибыли выглядит следующим образом:

Данные для расчетов используются согласно данным бухгалтерской отчетности (форма №1, форма №2, наличие и движение основных средств, затраты на производство, пояснения к бухгалтерскому балансу и отчету о финансовых результатах).

«Методы максимизации прибыли»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы

Считается, что прибыль будет на уровне максимума, если разница между совокупными затратами и между совокупной выручкой будет наиболее высокого значения. То есть на графике выше это можно проследить в точке $D$. Так как именно при выпуске продукции на уровне точки $D$ отрезок $AB$ является наибольшим между совокупной выручкой и совокупными затратами.

Предельный метод

На схеме 2 приведен пример определения максимизации прибыли предельным методом. Еще данный метод называется метод предельных доходов и издержек при максимизации прибыли.

Для того чтобы найти максимальный уровень прибыли коммерческого предприятия, нужно выявить значение средней прибыли, которое рассчитывается на одну дополнительную единицу выпускаемой продукции. То есть формула выглядит следующим образом:

• $AR$ — предельный доход,
• $AC$ – предельные совокупные издержки.

Часто в экономической теории предполагается, что коммерческая фирма действует в условиях совершенной конкуренции. Тогда средняя прибыль определяется по следующей формуле:

5.3 Маржинальный анализ и максимизация прибыли

Тогда общая прибыль находится по следующей формуле:

$Q$ — объем выпуска.

На схеме 2 выше можно увидеть линии средних общих издержек ($AC$), предельных издержек ($MC$) и средних переменных издержек ($AVC$). По оси абсцисс представлен объем выпуска продукции, а по оси ординат – цена.

Точка $E$ является точкой равновесия коммерческой фирмы ($E$), тогда объем выпуска в точке $E$ будет максимизировать прибыль. Точка $E$ располагается выше, чем средние затраты, а это значит, что средний доход (цена) буде выше, чем средние издержки. Отрезок $EK$ отражает значение средней прибыли, а площадь $PEKN$ – это значение совокупной прибыли.

Замечание 2

При значении равенства предельных затрат предельному доходу прибыль максимизируется при заданном объеме производства.

Источник: spravochnick.ru

Методы максимизации прибыли при формировании производственной программы предприятия

В рыночных условиях важное экономическое значение приобретает поиск оптимального варианта решения задачи, связанной с формированием производственной программы предприятия. Определение производственной программы с помощью современных моделей и математических методов оптимальных планов является одним из наиболее важных направлений поиска и дальнейшего использования внутрипроизводственных резервов и с целью повышения экономической эффективности работы предприятия.

Результатом формирования плана (годового, квартального, полугодового) предприятия является установление подлежащей изготовлению номенклатуры изделий и объемов их выпуска, а также обеспечение достижения одной или нескольких целей (максимизации прибыли или объема реализованной продукции, минимизация совокупной себестоимости запланированного объема выпуска по изделиям и др.). Состав критериев оптимальности, рекомендуемых к включению в модель задачи формирования производственной программы предприятия, определяется перспективными и текущими планами развития предприятия. Наиболее важные из них включаются в экономико-математическую модель задачи. В статье рассматривается вопрос формирования производственной программы предприятия на основе максимизации прибыли в стохастические постановки задачи, основные показатели и ограничения, применяемые при использовании данного метода, а также способы реализации поставленной задачи – метод гиперболического программирования и Чарнса и Купера.

гиперболического программирование
метод чарнса и купера
стохастическая постановка задачи
производственная программа предприятия

1. Закревская Е. А., Подходы и методы оценки стоимости компании в условиях рыночной экономики// Ученые записки российской академии предпринимательства 2009 № XVII. С. 168-177.

2. Лапшина Е.А., Савинова В.М., Анализ продуктов IBM для решения задач информационной бизнес-аналитики// Научные труды Вольного экономического общества России. 2012. Т. 164. С. 333-338.

При формировании производственной программы необходимо ориентироваться на потенциальные и фактические возможности предприятия по производству продукции, т.е. на производственную мощность и ограничения по годовому фонду имеющихся ресурсов.

Существует детерминированная и стохастическая постановки задачи планирования производственной программы предприятия. Стохастический подход к решению таких задач позволяет учитывать неопределённость в оптимизационных моделях.

Реальные прикладные задачи содержат либо некоторые неизвестные параметры, либо статистику изменения того или иного процесса. Этим они и отличаются от детерминированных задач оптимизации, которые формулируются с использованием заданных параметров.

Модели стохастического программирования используют знание распределений вероятностей для данных или их оценок. Цель здесь состоит в том, чтобы найти некоторое решение, которое является допустимым для всех (или почти всех) возможных значений данных и максимизируют математическое ожидание некоторой функции решений и случайных переменных. В общем, такие модели формулируются, решаются аналитически или численно, их результаты анализируются, чтобы обеспечить полезную информацию для лиц, принимающих решения.

Рассмотрим исходные данные

Таблица 1 Исходные данные по производимым продуктам

Значения показателей для изделий

Стоимость основных производственных фондов

Емкость рынка по изделию 1 составляет 16 единиц

Прибыль по изделиям

Статистика изменения прибыли

Таблица 2 Ограничения на использование ресурсов

Удельные затраты ресурсов

Годовой фонд ресурса

В рамках статьи рассмотрим постановку оптимизационной задачи годовой производственной программы многономенклатурного предприятия на основе максимизации прибыли.

Общий вид оптимизационной задачи в детерминированной постановке с дробно-линейной целевой функцией и линейными ограничениями имеет следующий вид:

,

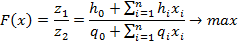
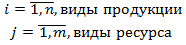
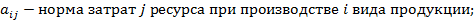
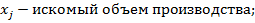
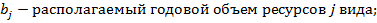
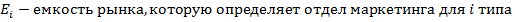
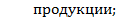
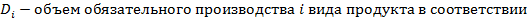
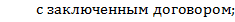
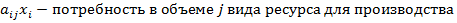
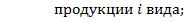
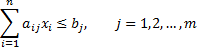
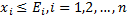
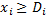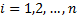
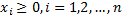
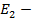
Эквипотенциали гиперболической функции в пространстве прямые, образующиеся вокруг некоторой точки. Для целевой функции

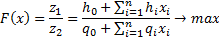
Такой точкой будет начало координат. Выражая из последнего уравнения 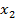, получим 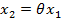, где 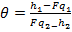. Уравнение 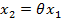геометрически представляется прямой, проходящей через начало координат. При изменении значения F будет изменяться и 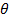, и прямая повернется вокруг начала координат. Чтобы установить поведение углового коэффициента 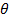при монотонном возрастании, необходимо взять производную от 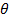по F:

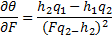
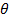
Знаменатель производной всегда положителен, а числитель не зависит от . Поэтому, знак производной постоянен, и угловой коэффициент будет либо только возрастать, либо только убывать, а прямая будет производить вращение только в одну сторону. Оптимум достигается в одной из вершин многогранника допустимых решений.

Эффективность использования тех или иных ресурсов для производства продукции является величиной случайной. Поэтому, необходимо максимизировать вероятность того, что прибыль от производства на типе j цеха будет равна или больше заданной величине ?.

Тогда задачу можно записать в виде:

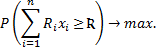
При ограничениях на производственные возможности:

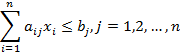
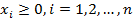
, где

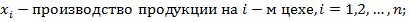
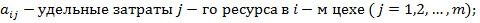
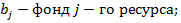
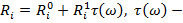
Задачу в вероятностной постановке можно свести к детерминированному эквиваленту. Допустим, прибыль от эксплуатации определяется по формуле: случайная величина.

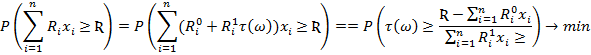
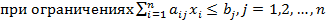и

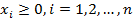
Получим исходя из статистики распределения прибыли. За 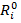примем минимальное значение прибыли по каждому изделию, а 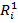– среднее отклонение значений прибыли от средней величины по каждому изделию. Тогда получим:

Таблица 3 Численные значения прибыли

Составляющие расчета прибыли

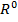
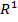
Численное выражение поставленной задачи имеет вид:

, ,

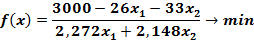
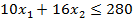
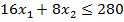
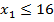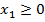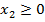
Для получения оптимального плана производства в поставленной выше задаче необходимо изучить алгоритмы выбранных методов поиска решения.

Первым из них является метод гиперболического программирования. Метод основан на использовании симплексной техники пересчета и специальном выборе разрешающего столбца. Ограничения поставленной задачи записываются в решающую матрицу обычным образом и дополняются базисом.

Также симплекс таблица предусматривает еще три дополнительных строки: вторая и третья – это коэффициенты, стоящие в числители и знаменатели соответственно. В первой строке фиксируются признаки оптимальности. Если в исходной задаче знаменатель отличен от нуля, можно переходить к решению.

Если же знаменатель обращается в ноль, необходимо сделать шаг модифицированных жордановский исключений для того, чтобы получить опорный план решения задачи. Признаки оптимальности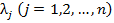

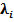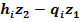рассчитываются по формуле =.

Разрешающий столбец определяется по правилу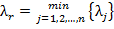. Выбор разрешающего элемента в столбце r проводится обычным образом – по минимальному симплекс отношению. Симплекс-таблица (за исключением первой строки) пересчитывается по рекуррентным формулам. Признаки оптимальности пересчитываются по формулам выше после пересчета остальных элементов. Критерием окончания процесса является 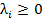, 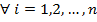[1, 274-275].

Таблица 4 Исходная симплекс-таблица решения задачи оптимизации методом гиперболического программирования

В точке 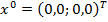целевая функция не существует. Поэтому необходимо сделать шаг жордановых исключений и перейти в такую вершину выпуклого многогранника, образованного ограничениями выше, где функция 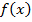существует. Применив правило 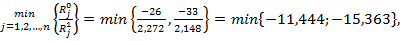получаем, что разрешающий столбец – второй. Определяя по минимальному симплекс отношению разрешающий элемент, производится пересчет таблицы по рекуррентным формулам, и получаем следующую симплекс-таблицу.

Таблица 5 Промежуточная симплекс-таблица методы гиперболического программирования

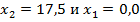
В найденной точке функция существует, и можно определить признаки оптимальности (верхняя строка полученной симплекс-таблицы). Разрешающий столбец с отрицательным числом -2452,6. Найдя в этом столбце разрешающий элемент (11) и пересчитав симплекс-таблицу, получаем следующую таблицу.

Таблица 11 Промежуточная симплекс-таблица методы гиперболического программирования

Признаки оптимальности последней симплекс-таблицы положительны, следовательно, получено оптимальное решение поставленной задачи: 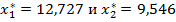. Значение целевой функции получим, подставив получившиеся значения 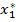и 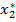или сменив знак у величины, стоявшей в правом верхнем углу симплекс-таблицы: f ( 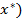= 47,638.

Если учесть возможность выпуска продукции только в целых количествах, получим следующий результат: , .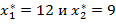

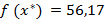Второй метод, который применяется для решения задач с дробно-линейной функций, метод Чарнса и Купера.

Задача, представленная в стандартном виде как:

В исходном виде задача представлена следующим образом:

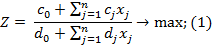
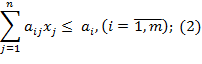
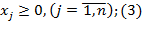
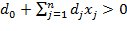
Кроме того, предполагается, что в области неотрицательных решений системы уравнений (2) имеет место .

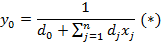
И получим новые переменные:

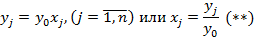
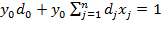
Из выражения (*) имеем: .

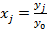
Подставим в это выражение .

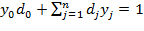
Получим .

Теперь исходная задача приобретает следующий вид:

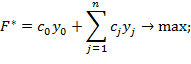
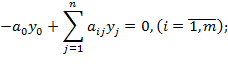
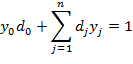
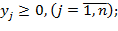
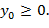
Для реализации метода Чарнса и Купера введем новую переменную:

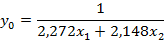
Заменим: 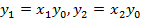или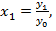

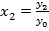
Тогда 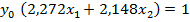. Подставив в равенство 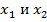получим: .

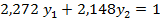Теперь исходная задача приобретает следующий вид:

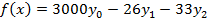
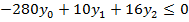
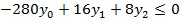
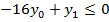
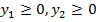
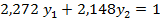
Решая систему выше, используя Microsoft Excel 2010 (надстройку: поиск решения), получаем следующее решение эквивалетной задачи: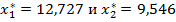

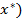, f ( =47,638.

Если учитывать, что продукция выпускается в целых величинах, то получаем: , .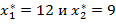

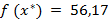После того как проведены численные расчеты методом гиперболического программирования и методом Чарнса и Купера можно сделать вывод о том, что оба они привели к одному и тому же результату, а именно: 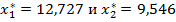, f ( 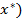=47,638. В целых значениях: , .

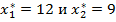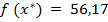Оба метода схожи в реализации, оба имеют несколько итераций, результатом проведения которых является оптимальное решение поставленной задачи.

Метод гиперболического программирования имеет ряд преимуществ, например, на каждом шаге заметно, как изменяется значение целевой функции и т.д. Его несложно реализовать для задачи, когда компания реализует небольшое количество продуктов и необходимо оптимизировать их производство. С увеличением размерности, будет усложняться реализация каждой итерации, увеличиваться время на нее. Так же ошибившись на любом шаге с выбором разрешающего столбца или элемента, можно увеличить число итераций в рамках реализации задачи.

Однако, по- моему мнению, метод Чарнса и Купера проще реализовать, он может быть применен к задаче любой размерности и решение данным способом можно получить, используя простейшие компьютерные продукты, например Microsoft Excel. В результате мы получаем оптимальное решение поставленной задачи, применив лишь набольшие усилия на первом шаге по приведению задачи к линейному виду.

Источник: eduherald.ru

19.2. Максимизация прибыли

Систематическое получение прибыли является необходимой целью предпринимательской деятельности любого предприятия. Поэтому доминирующей проблемой для предприятия является максимизация прибыли, что означает разработку стратегии на систематическое увеличение прибыли и минимизацию издержек. Данная задача многоплановая, вот почему для своего решения она требует системного подхода.

Для принятия решений часто требуется знать сумму прибыли, которую получает предприятие в расчете на единицу продукции при данном объеме реализации и цене, диктуемой спросом. При определении продажной цены используют среднюю прибыль (An) и предельную прибыль (Мn):

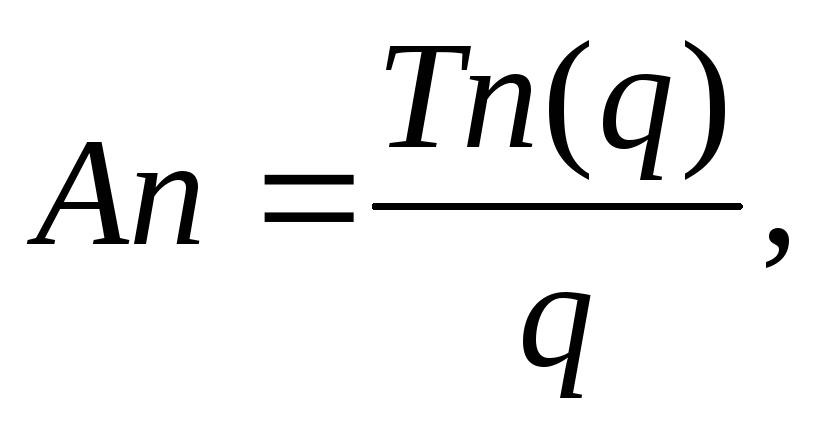
(19.1)

где Tn(q) — совокупная сумма прибыли на определенный товар за определенный период;

q — объем продаж.

Из этого следует, что максимизация прибыли связана с процессом приращения предпринимательской прибыли. Это, в свою очередь, означает, что в расчетах требуется использование предельных величин: предельной прибыли, предельного дохода и предельных издержек. Иными словами, прибыль максимизируется в точке, в которой любое, даже малое приращение объема реализации (выпуска) продукции оставляет прибыль без изменения, т.е. приращение прибыли при приращении объема (реализации) продукции равняется нулю. Математически это можно записать так:

Mn(q)=MR(q) –MC(q) = 0, (19.2)

где Mn(q) — предельная прибыль от объема продукции;

MR(q) — предельный доход (выручка) от объема продукции;

МС(q) — предельные издержки от объема продукции.

Из формулы (19.2) следует, что прибыль максимизируется в том случае, когда предельные издержки равны предельному доходу:

Поясним это на примере работы консервного комбината. Данные о выпуске количества консервов, валовых постоянных издержках, относимых на соответствующее производство, валовых переменных издержках, относимых на соответствующий выпуск продукции, валовых издержках производства и обращения, а также результаты расчета средних и предельных издержек, указанные в тысячах рублях на единицу изделия, приведены в табл. 19.1 (цифры для удобства округлены).

Расчет максимальной прибыли в зависимости от объема продукции, цены и издержек

Валовый доход (выручка) (тыс. руб.), TР

Валовые издержки (тыс. руб.), ТС

Валовая прибыль (тыс. руб.), М = гр. 3-— гр.4

Предельный доход (руб./шт.), MR

Предельные издержки (руб./шт.), МС

Предельная прибыль (руб./шт.), Мп

Графа 2 табл. 19.1 содержит данные о цене спроса, соответствующие количеству возможной реализации консервов. Функция спроса от цены получена на основе линейного уравнения

q = — 4,78р + 13712,1.

Коэффициент эластичности спроса в зависимости от изменения цены для разного количества продаж исчисляется по формуле:

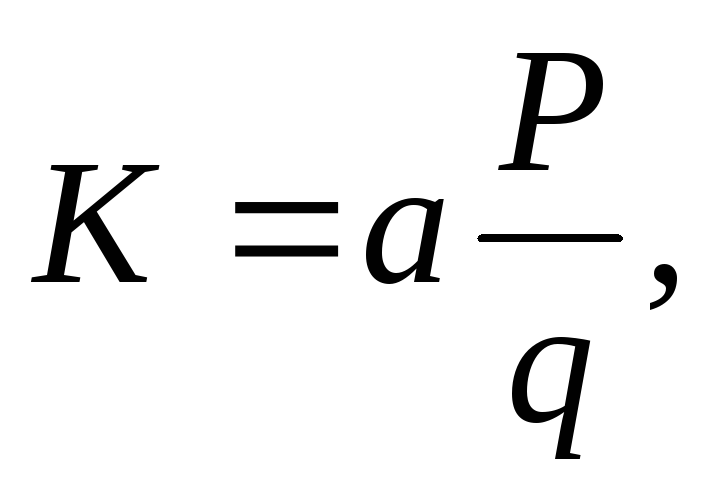
(19.3)

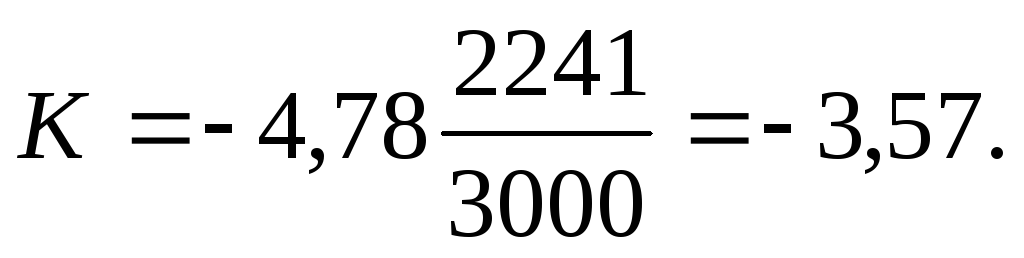
В количестве 3000 шт.

В количестве 6000 шт.

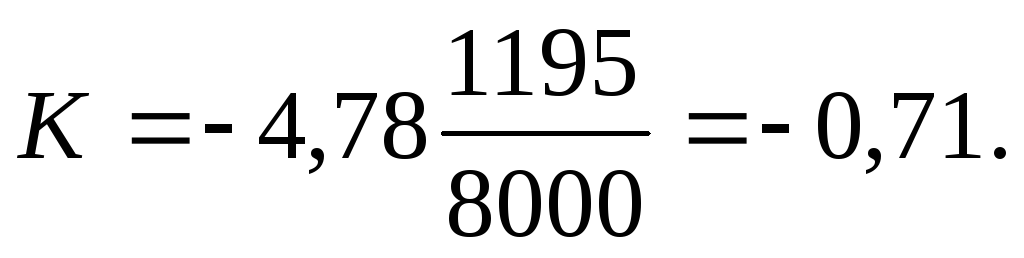
В количестве 8000 шт,

При больших объемах продаж спрос становится неэластичным. Предельные величины дохода (выручки), издержек и прибыли получаются путем вычитания из данных валового дохода (гр. 3), валовых издержек (гp. 4) и валовой прибыли (гр. 5) соответствующих значений из предыдущей строки.

Например, предельная прибыль:

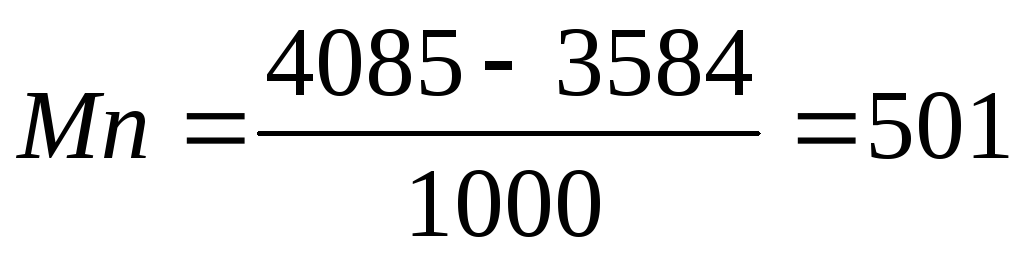
для объема продаж 5000 шт.: руб.

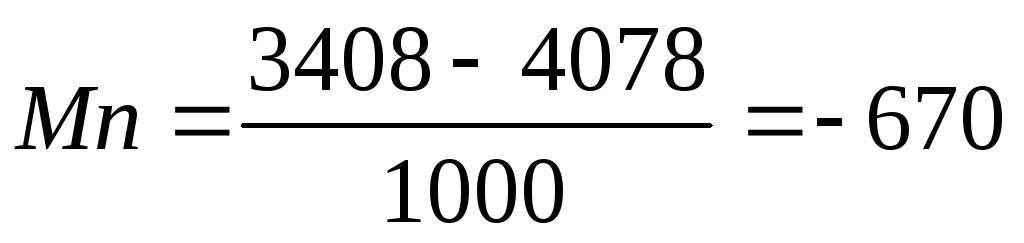
для объема продаж 7000 шт.: руб.

Деление на 1000 необходимо потому, что предельные (приростные) показатели определяются в расчете на единицу продукции в рублях.

Для наглядности на основании данных табл. 19.1 построим графики (рис. 19.3 и 19.4).

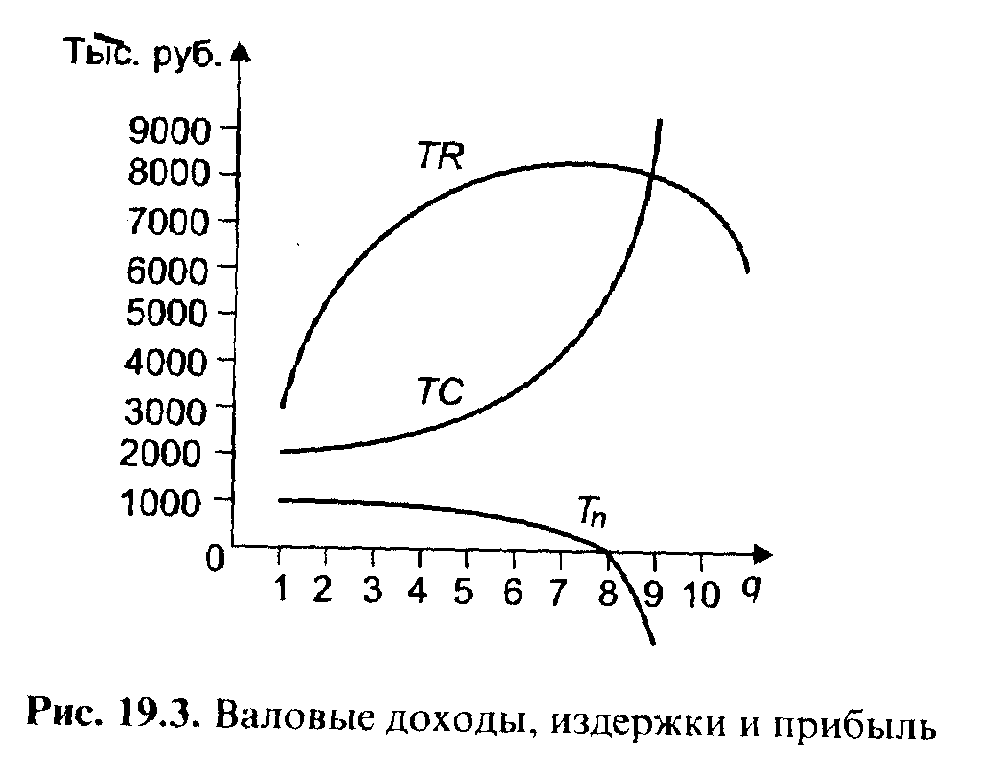
Из табл. 19.1 и рис. 19.3 и 19.4 следует, что наибольшие объемы реализации не всегда дают наибольшие суммы прибыли. Максимальную сумму прибыли предприятие может получить при объеме реализации более 5 тыс. шт. и менее 6 тыс. шт. банок консервов. При этом цена одной банки составляет примерно 1600 руб.

Если количество реализованных банок консервов превышает 6 тыс. шт., то сумма прибыли уменьшается, а при 9 тыс. шт. предприятие понесет убытки в размере 436 тыс. руб., которые при реализации 10 тыс. шт. могут возрасти почти до 6 млн. руб.

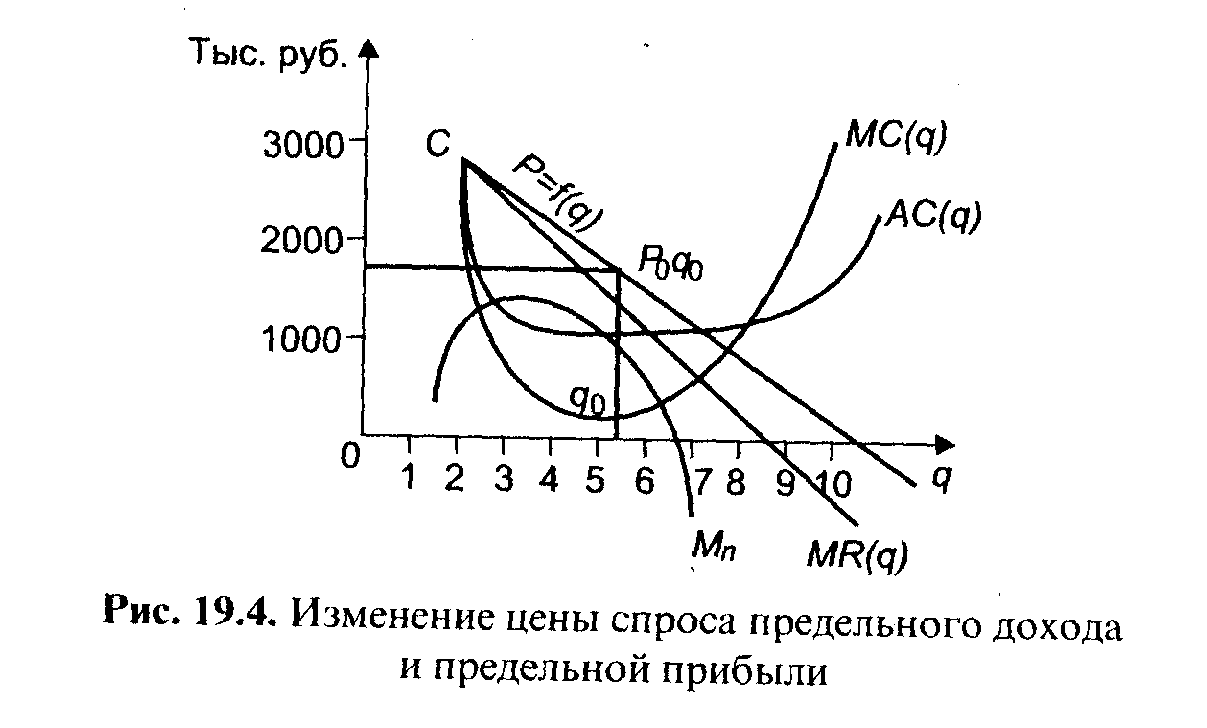
Предельные показатели позволяют более четко судить о скорости изменения их значений (рис. 19.4).

Точка пересечения предельного дохода MR(q) с предельными издержками MC(q) определяет максимум прибыли. В этой точке предельная прибыль равна нулю, а ее кривая пересекает ось абсцисс. За данными пределами начинаются убытки, которые будут снижать сумму валовой прибыли.

Для того чтобы решить вопрос максимизации прибыли, важно также знать, действует ли предприятие в условиях свободной конкуренции или монопольного рынка. Пищевые предприятия, в частности, реализуют свою продукцию в условиях свободной конкуренции. А это означает, что за цену реализации своей продукции оно принимает ту, которую задает рынок.

Итак, для предприятия максимизация прибыли заключается в выборе такого объема реализации продукции, при котором предельные издержки предприятия в производстве и при реализации равнялись бы рыночной цене. Математически это можно представить следующим образом:

Иными словами, на рынке свободной конкуренции доход равен рыночной цене. Покажем это на примере рыбоперерабатывающего предприятия, выпускающего икру в банках. Данные о производстве, издержках, прибыли, а также о предельных величинах приведены в табл. 19.2.

Экономические показатели и расчеты предельных величин, руб.

Выпуск банок, шт.

Валовой доход (выручка), TR

Источник: studfile.net