Метод ветвей и границ код программы

На языке программирования C++ разработать программу решения задачи коммивояжёра методом ветвей и границ.

Математическая часть

Задача коммивояжёра (коммивояжёр — бродячий торговец) заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.

Существует масса разновидностей обобщённой постановки задачи, в частности геометрическая задача коммивояжёра (когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра.

Простейшие методы решения задачи коммивояжёра: полный лексический перебор, жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешёвого включения), метод минимального остовного дерева. На практике применяются различные модификации более эффективных методов: метод ветвей и границ и метод генетических алгоритмов, а также алгоритм муравьиной колонии.

Введение в программирование №15. Метод ветвей и границ, естественные алгоритмы

Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jТ=(1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t=(j1,j2. jn,j1), причём все j1..jn – разные номера; повторяющийся в начале и в конце j1, показывает, что перестановка зациклена. Расстояния между парами вершин Сij образуют матрицу С. Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать функционал

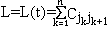
Метод ветвей и границ

К идее метода ветвей и границ приходили многие исследователи, но Литтл с соавторами на основе указанного метода разработали удачный алгоритм решения ЗК и тем самым способствовали популяризации подхода. С тех пор метод ветвей и границ был успешно применен ко многим задачам, для решения ЗК было придумано несколько других модификаций метода, но в большинстве учебников излагается пионерская работа Литтла.

Общая идея тривиальна: нужно разделить огромное число перебираемых вариантов на классы и получить оценки (снизу – в задаче минимизации, сверху – в задаче максимизации) для этих классов, чтобы иметь возможность отбрасывать варианты не по одному, а целыми классами. Трудность состоит в том, чтобы найти такое разделение на классы (ветви) и такие оценки (границы), чтобы процедура была эффективной.

Нам будет удобнее трактовать Сijкак стоимость проезда из городаiв городj. Допустим, что добрый мэр городаjиздал указ выплачивать каждому въехавшему в город коммивояжеру 5 долларов. Это означает, что любой тур подешевеет на 5 долларов, поскольку в любом туре нужно въехать в городj.

Пример 1 максимум. Метод ветвей и границ для решения задач целочисленного линейного программирования

Но поскольку все туры равномерно подешевели, то прежний минимальный тур будет и теперь стоить меньше всех. Добрый же поступок мэра можно представить как уменьшение всех чиселj-го столбца матрицы С на 5. Если бы мэр хотел спровадить коммивояжеров изj-го города и установил награду за выезд в размере 10 долларов, это можно было бы выразить вычитанием 10 из всех элементовj-й той строки. Это снова бы изменило стоимость каждого тура, но минимальный тур остался бы минимальным. Итак, доказана следующая лемма.

Вычитая любую константу из всех элементов любой строки или столбца матрицы С, мы оставляем минимальный тур минимальным.

Для алгоритма нам будет удобно получить побольше нулей в матрице С, не получая там, однако, отрицательных чисел. Для этого мы вычтем из каждой строки ее минимальный элемент (это называется приведением по строкам, см. табл. 3), а затем вычтем из каждого столбца матрицы, приведенной по строкам, его минимальный элемент, получив матрицу, приведенную по столбцам, см. табл. 4).

Прочерки по диагонали означают, что из города iв городiходить нельзя. Заметим, что сумма констант приведения по строкам равна 27, сумма по столбцам 7, сумма сумм равна 34.

Тур можно задать системой из шести подчеркнутых (выделенных другим цветом) элементов матрицы С, например, такой, как показано на табл. 2. Подчеркивание элемента означает, что в туре изi-го элемента идут именно вj-тый. Для тура из шести городов подчеркнутых элементов должно быть шесть, так как в туре из шести городов есть шесть ребер.

Каждый столбец должен содержать ровно один подчеркнутый элемент (в каждый город коммивояжер въехал один раз), в каждой строке должен быть ровно один подчеркнутый элемент (из каждого города коммивояжер выехал один раз); кроме того, подчеркнутые элементы должны описывать один тур, а не несколько меньших циклов. Сумма чисел подчеркнутых элементов есть стоимость тура. На табл. 2 стоимость равна 36, это тот минимальный тур, который получен лексикографическим перебором.

Теперь будем рассуждать от приведенной матрицы на табл. 2. Если в ней удастся построить правильную систему подчеркнутых элементов, т.е. систему, удовлетворяющую трем вышеописанным требованиям, и этими подчеркнутыми элементами будут только нули, то ясно, что для этой матрицы мы получим минимальный тур. Но он же будет минимальным и для исходной матрицы С, только для того, чтобы получить правильную стоимость тура, нужно будет обратно прибавить все константы приведения, и стоимость тура изменится с 0 до 34. Таким образом, минимальный тур не может быть меньше 34. Мы получили оценку снизу для всех туров.

Теперь приступим к ветвлению. Для этого проделаем шаг оценки нулей. Рассмотрим нуль в клетке (1,2) приведенной матрицы. Он означает, что цена перехода из города 1 в город 2 равна 0. А если мы не пойдем из города 1 в город 2? Тогда все равно нужно въехать в город 2 за цены, указанные во втором столбце; дешевле всего за 1 (из города 6).

Далее, все равно надо будет выехать из города 1 за цену, указанную в первой строке; дешевле всего в город 3 за 0. Суммируя эти два минимума, имеем 1+0=1: если не ехать “по нулю” из города 1 в город 2, то надо заплатить не меньше 1. Это и есть оценка нуля. Оценки всех нулей поставлены на табл. 5 правее и выше нуля (оценки нуля, равные нулю, не ставились).

Выберем максимальную из этих оценок (в примере есть несколько оценок, равных единице, выберем первую из них, в клетке (1,2)).

Итак, выбрано нулевое ребро (1,2). Разобьем все туры на два класса – включающие ребро (1,2) и не включающие ребро (1,2). Про второй класс можно сказать, что придется приплатить еще 1, так что туры этого класса стоят 35 или больше.

Что касается первого класса, то в нем надо рассмотреть матрицу на табл. 6 с вычеркнутой первой строкой и вторым столбцом.

Источник: studfile.net

Clever-Shadow/python-salesman

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags

Nothing to show

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Cancel Create

• Local
• Codespaces

HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

Latest commit message
Commit time

README.md

Задача коммивояжера на Python методом ветвей и границ(алгоритм Литтла).

Задача коммивояжера — одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город.

В основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества. На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет. Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве.

Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено. Проверяемое подмножество может быть отброшено еще и в том случае, когда в нем удается найти наилучшее решение. Если значение целевой функции на найденном решении меньше рекорда, то происходит смена рекорда.

По окончанию работы алгоритма рекорд является результатом его работы. Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т.д.

Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующую последовательность действий:
1 — Построение матрицы с исходными данными.
2 — Нахождение минимума по строкам.
3 — Редукция строк.
4 — Нахождение минимума по столбцам.
5 — Редукция столбцов.
6 — Вычисление оценок нулевых клеток.
7 — Редукция матрицы.
8 — Если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9.
9 — Вычисление итоговой длины пути и построение маршрута.

Для тестов можно использовать следующее:
Test1
4
0 10 1 1
10 0 1 5
1 1 0 10
1 5 10 0

Test2
4
0 5 11 9
10 0 8 7
7 14 0 8
12 6 15 0

Test3
3
0 5 10
5 0 7
10 7 0

Test4
4
0 10 1 7
10 0 6 1
1 6 0 10
7 1 10 0

Test5
4
0 1 1 7
1 0 7 1
1 7 0 1
7 1 1 0

Test6
4
0 1 1 7
1 0 20 1
1 20 0 1
7 1 1 0

Test7
4
0 1 6 3
1 0 1 9
6 1 0 1
3 9 1 0

Test8
6
0 5 7 6 8 3
1 0 8 4 6 2
3 9 0 6 5 3
7 8 4 0 4 2
2 7 5 6 0 6
5 2 6 4 5 0

Источник: github.com

Русские Блоги

Алгоритм и структура данных (десять): метод ветвей и границ FIFO (задача коммивояжера) (реализация на C ++)

Каталог статей

• Алгоритм и структура данных (десять): метод ветвей и границ FIFO (задача коммивояжера) (реализация на C ++)

• Основная идея метода ветвей и границ
• Проблема коммивояжера (TSP)
• Основная функция
• Ссылка: Анализ и разработка алгоритмов (описание C ++) Под редакцией Ши Чжиго, Лю Цзивэй, Яо Ифэй

Алгоритм и структура данных (десять): метод ветвей и границ FIFO (задача коммивояжера) (реализация на C ++)

Основная идея метода ветвей и границ

Метод ветвей и границ часто ищет дерево пространства решений проблемы в первую очередь в ширину или с наименьшими затратами (максимальная выгода). Дерево пространства решений проблемы — это упорядоченное дерево, которое представляет пространство решений проблемы. Обычно используются деревья подмножеств и деревья перестановок.

При поиске в дереве пространства решений проблемы метод ветвей и границ и метод обратного отслеживания используют разные методы расширения для текущего узла раскрытия. В методе ветвей и границ каждый активный узел имеет только один шанс стать расширенным узлом. Как только активный узел становится узлом расширения, он сгенерирует сразу все свои дочерние узлы.

Среди этих дочерних узлов те, которые приводят к недопустимым или неоптимальным решениям, отбрасываются, а оставшиеся дочерние узлы добавляются в таблицу активных узлов. После этого выберите следующий узел из таблицы активных узлов, который станет текущим узлом расширения, и повторите процесс расширения узла, описанный выше. Этот процесс продолжается до тех пор, пока не будет найдено желаемое решение или пока таблица узлов скольжения не станет пустой.

Метод ветвей и границ в стиле очереди (FIFO): организуйте таблицу активных узлов в очередь и выберите следующий узел в качестве текущего расширенного узла в соответствии с принципом очереди «первым пришел — первым ушел».

Проблема коммивояжера (TSP)

Продавец хочет продавать товары в нескольких городах, и ему известны транспортные расходы (или командировочные расходы) между городами. Он должен выбрать маршрут, который начинается от станции, проходит через каждый город и, наконец, возвращается на станцию, чтобы сделать общий маршрут (или общую стоимость поездки наименьшей).

Основная функция

/ * Разветвленное решение задачи коммивояжера * / #include using namespace std; const int NoEdge = -1; const int MAX = 20; int G[MAX][MAX]; int ans[MAX], x[MAX]; int bestc, cc; void init(int n) < int i, j, len; memset(G, NoEdge, sizeof(G)); while (cin >> i >> j) < if (i == 0 j == 0) break; cin >> len; G[i][j] = len; G[j][i] = len; > for (i = 1; i void Swap(int j) < int temp; temp = i; i = j; j = temp; >void Traveling(int i, int n) < int j; if (i == (n + 1)) < if ((G[x[n — 1]][x[n]] != NoEdge) ((cc + G[x[n]][1]) < bestc) G[x[n]][1] != NoEdge) < for (j = 1; j < n; j++) ans[j] = x[j]; bestc = cc + G[x[n]][1]; >> else < for (j = i; j > > > void print(int n) < cout «; cout int main() < int n; cout > nn) < cout return 1; >

n представляет собой общее количество городов, bestc хранит наименьшую стоимость поездки, а ans [i] хранит оптимальный маршрут путешествия. Результат работы программы показан на рисунке ниже:

Источник: russianblogs.com