Метод монте карло пример программы

Монте-Карло — метод анализа, применяемый в случаях, когда параметры известны приблизительно, и есть информация о статистическом распределении этих параметров. Для проведения анализа генерируют большое число случайных значений параметров, для каждого такого значения выполняют расчет и формируют статистическое распределение для результата.

Примерами задач, для которых применяют анализ Монте-Карло, могут служить следующие ситуации :

• Оценка опционов на акции на основе статистических данных о колебаниях цены акции.
• Определение Value-at-Risk в инвестиционных решениях с известными данными о статистическом распределении доходности ценной бумаги.
• Оценка инвестиционных проектов, связанных с добычей полезных ископаемых или другой деятельностью, в которой данные о параметрах проекта (дебит нефтяной скважины и т. п.) выражены статистически.

Пример графика распределения значений NPV инвестиционного проекта методом Монте-Карло:

Что такое метод Монте-Карло (простым языком)

На этом графике по горизонтальной оси показан интервал значений NPV, полученных в расчетах (результаты сгруппированы с шагом 100 000), а по вертикальной оси — число случаев, когда NPV попадала в этот интервал (из 1 000 попыток).

Алгоритм метода Монте-Карло

В сфере финансов для анализа методом Монте-Карло необходимо выполнить следующие шаги:

Шаг 1. Параметры

Выбираем результат, который будем анализировать методом Монте-Карло — цена опциона, NPV инвестиционного проекта и т. п.

В качестве параметров для Монте-Карло выбираем один или несколько показателей, влияющих на результат . Предполагается, что значения этих параметров известны не точно, но мы знаем или можем получить характеристики статистического распределения параметров.

Шаг 2. Основная модель

Создаем модель, которая вычисляет результат с учетом выбранных параметров. Скорее всего, кроме статистических параметров, используемых в Монте-Карло, в ней будут и другие данные, которые заданы в традиционном виде с конкретными значениями. В финансовом анализе модель обычно создают в Excel, но, в принципе, метод Монте-Карло можно реализовать и другими инструментами : на языке Python или еще в каком-то приложении.

Шаг 3. Закон распределения

Необходимо решить, как именно выглядит статистическое распределение параметров. Простейший вариант — равномерное распределение. В этом случае параметр с одинаковой вероятностью может принимать любое из значений в заданном интервале. К сожалению, такое распределение случайных величин не очень часто соответствует действительности.

Самый распространенный подход — нормальное распределение , предполагающее, что вероятность выпадения значений постепенно падает с удалением от среднего. Хотя в реальных процессах нормальное распределение часто лучше всего описывает поведение параметров, у него есть неудобства в реализации. Во-первых, оно не ограничивает возможные отклонения от среднего.

Пусть и с маленькой вероятностью, но значение параметра может оказаться сколь угодно далеким от ожидаемого. Из-за этого нормальное распределение иногда заменяют треугольным. Во-вторых, нормальное распределение с одинаковой вероятностью допускает отклонения параметра вверх и вниз от ожидаемой величины. Но часто вероятности снижения и роста показателя не одинаковы. Тогда может потребоваться более сложный закон распределения.

Шаг 4. Свойства распределения

Для выбранного закона распределения случайных параметров необходимо получить свойства этого распределения. В наиболее популярном нормальном распределении это среднее значение и стандартное отклонение. Если Монте-Карло будет использовать другое распределение, то и перечень его свойств может меняться.

Самая интересная (и сложная) деталь на этом шаге — корреляция . Если параметров несколько, то может оказаться, что они хотя и являются случайными, но их случайные колебания связаны друг с другом. Например, если при моделировании инвестиционного проекта в качестве случайных параметров выбраны цены готовой продукции и стоимость комплектующих, то жизненный опыт подсказывает, что чаще всего цены на товар и цены на комплектующие к нему меняются похожим образом, то есть эти величины коррелированы. Анализ их случайных колебаний без учета такой связи может заметно исказить картину.

Шаг 5. Многократный расчет

С помощью средств автоматизации расчетов (Excel, Python и т. п.) запускаем цикл из большого числа повторений, на каждом шагу которого получаем случайные значения параметров в соответствии с их законом распределения, вычисляем результат и накапливаем статистику по полученному результату.

Шаг 6. Анализ результатов

В первую очередь результаты моделирования представляют графически, отображая на гистограмме частоту попадания результата в разные интервалы значений. Далее можно рассчитать для результата любые статистические характеристики как для реального случайного процесса: среднее, стандартное отклонение и другие показатели.

Сложности применения Монте-Карло

Главная проблема анализа методом Монте-Карло связана с получением данных о статистическом распределении параметров, использованных в анализе. Сложный и насыщенный данными метод моделирования создает у аналитика впечатление о точности и глубине исследования возможных результатов, но в действительности качество сделанных выводов полностью зависит от качества исходных данных .

В ряде случаев для параметров доступны обширные данные наблюдений, и их статистику можно объективно рассчитать. Но часто наблюдения для параметров недоступны, и правила их распределения определяют аналитически. В таких ситуациях можно сделать две ошибки.

Ошибка 1. Неверное правило распределения. Закон распределения и его характеристики не стыкуются с тем, как определи базовые значения параметров. Например, продажи уже и так спланированы по наиболее оптимистическому сценарию, а статистическое распределение в равной степени допускает отклонения как вверх, так и вниз.

Ошибка 2. Игнорирование корреляции. Многие параметры, хотя и являются случайными, сильно связаны друг с другом. Если мы анализируем их как независимые, то можем получить сильно искаженный результат.

Организация расчета методом Монте-Карло в Excel

Простые решения для анализа Монте-Карло можно реализовать своими силами. Ниже приведены два видеоролика о том, как создать модель анализа Монте-Карло средствами таблиц данных или с применением макросов.

1. Вариант с использованием таблиц данных:
Файл из видео: monte-carlo-datatable.zip

2. Вариант с использованием макросов:
Файл из видео: monte-carlo-macro.zip

Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.

Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.

Источник: www.alt-invest.ru

Метод Монте-Карло и его точность

Под метдом Монте-Карло понимается численный метод решения
математических задач при помощи моделирования случайных величин. Представление об истории метода и простейшие примеры его применения можно найти в Википедии.

В самом методе нет ничего сложного. Именно эта простота объясняет популярность данного метода.

Метод имеет две основных особенности. Первая — простая структура вычислительного алгоритма. Вторая — ошибка вычислений, как правило, пропорциональна
, где — некоторая постоянная, а — число испытаний. Ясно, что добиться высокой точности на таком пути невозможно. Поэтому обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью.

Однако одну и ту же задачу можно решать различными вариантами метода Монте-Карло, которым отвечают различные значения . Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее значение .

Общая схема метода

Допустим, что нам требуется вычислить какую-то неизвестную величину m. Попытаемся придумать такую случайную величину , чтобы . Пусть при этом .
Рассмотрим независимых случайных величин (реализаций), распределения которых совпадают с распределением . Если достаточно велико, то согласно центральной предельной теореме распределение суммы будет приблизительно нормальным с параметрами , .

На основе Центральной предельной теоремы (или если хотите предельной теоремы Муавра-Лапласа) не трудно получить соотношение:

где — функция распределения стандартного нормального распределения.

Это — чрезвычайно важное для метода Монте-Карло соотношение. Оно дает и метод расчета , и оценку погрешности.

В самом деле, найдем значений случайной величины . Из указанного соотношения видно, что среднее арифметическое этих значений будет приближенно равно . С вероятностью близкой к ошибка такого приближения не превосходит величины . Очевидно, эта ошибка стремится к нулю с ростом .

В зависимости от целей последнее соотношение используется по разному:

Если взять k=3, то получим так называемое «правило »:

Точность вычислений

Как видно из приведенных выше соотношений, точность вычислений зависит от параметра и величины – среднеквадратичного отклонения случайной величины .

В этом пункте хотелось бы указать важность именно второго параметра . Лучше всего это показать на примере. Рассмотрим вычисление определенного интеграла.

Вычисление определенного интеграла эквивалентно вычислению площадей, что дает интуитивно понятный алгоритм вычисления интеграла (см. статью в Википедии). Я рассмотрю более эффективный метод (частный случай формулы для которого, впрочем, тоже есть в статье из Википедии). Однако не все знают, что вместо равномерно распределенной случайной величины в этом методе можно использовать практически любую случайную величину, заданную на том же интервале.

Итак, требуется вычислить определенный интеграл:

Выберем произвольную случайную величину с плотностью распределения , определенной на интервале . И рассмотрим случайную величину .

Математическое ожидание последней случайной величины равно:

Таким образом, получаем:

Последнее соотношение означает, что если выбрать значений , то при достаточно большом :

Таким образом, для вычисления интеграла, можно использовать практически любую случайную величину . Но дисперсия , а вместе с ней и оценка точности, зависит от того какую случайную величину взять для проведения расчетов.

Можно показать, что будет иметь минимальное значение, когда пропорционально |g(x)|. Выбрать такое значение в общем случае очень сложно (сложность эквивалентна сложности решаемой задачи), но руководствоваться этим соображением стоит, т.е. выбирать распределение вероятностей по форме схожее с модулем интегрируемой функции.

Численный пример

Теория, конечно, дело хорошее, но давайте рассмотрим численный пример: ; ; .

Вычислим значение интеграла с применением двух различных случайных величин.

В первом случае будем использовать равномерно распределенную случайную величину на [a,b], т.е. .

Во втором случае возьмем случайную величину с линейной плотностью на [a,b], т.е. .

Вот график, указанных функций

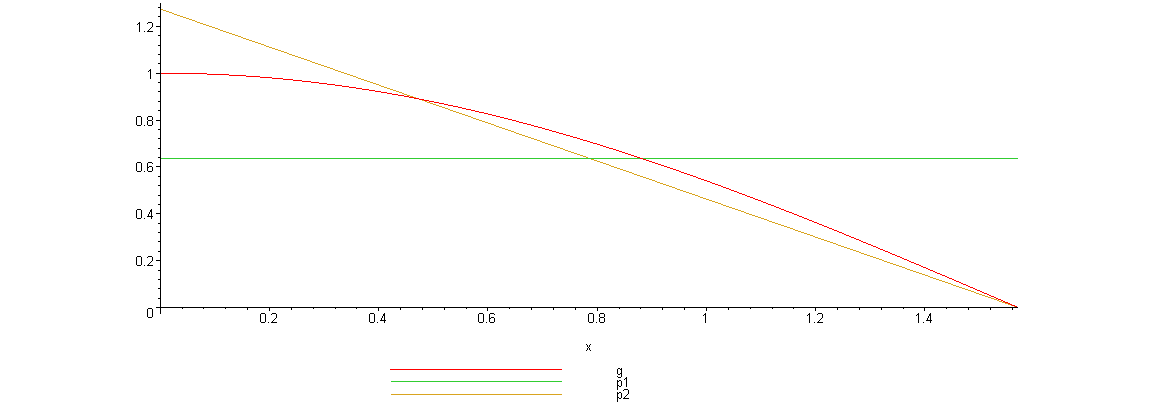
Нетрудно видеть, что линейная плотность лучше соответствует функции .

Код программы модельного примера в математическом пакете Maple

restart; with(Statistics): with(plots): #исходные функции g:=x->cos(x): a:=0: b:=Pi/2: N:=10000: #плотности распределений p1:=x->piecewise(x>=a and xpiecewise(x>=a and x

Файл с данной программой можно взять тут

Точное значение интеграла легко вычислить аналитически, оно равно 1.

Результаты одного моделирования при :

Для равномерно распределенной случайной величины: .

Для случайной величины с линейной плотностью распределения: .

В первом случае относительная погрешность более 21%, а во втором 2.35%. Точность в первом случае равна 0.459, а во втором – 0.123.

Думаю, данный модельный пример показывает важность выбора случайной величины в методе Монте-Карло. Выбрав, правильную случайную величину, можно получить более высокую точность вычислений, при меньшем числе итераций.

Конечно, так не вычисляют одномерные интегралы, для этого есть более точные квадратурные формулы. Но ситуация меняется при переходе к многомерным интегралам, т.к. квадратурные формулы становятся громоздкими и сложными, а метод Монте-Карло применяется лишь с небольшими изменениями.

Количество итераций и генераторы случайных чисел

Не трудно видеть, что точность вычислений зависит от количества случайных величин включенных в сумму. Причем, для увеличения точности вычислений в 10 раз нужно увеличить в 100 раз.

При решении некоторых задач для получения приемлемой точности оценки требуется брать очень большое число . А учитывая, что метод зачастую работает очень быстро, то реализовать последнее при современных вычислительных возможностях совсем не сложно. И возникает соблазн просто увеличить число .

Если в качестве источника случайности используется некоторое физическое явление (физический датчик случайных чисел), то все работает отлично.

Часто для вычислений по методу Монте-Карло применяют датчики псевдослучайных чисел. Главная особенность таких генераторов – наличие некоторого периода.

Метод Монте-Карло можно использовать при значениях не превышающих (лучше много меньших) период вашего генератора псевдослучайных чисел. Последний факт вытекает из условия независимости случайных величин, используемых при моделировании.

При проведении больших расчетов нужно убедиться, что свойства генератора случайных чисел позволяют вам провести эти расчеты. В стандартных генераторах случайных чисел (в большинстве языков программирования) период чаще всего не превосходит 2 в степени разрядности операционной системы, а то и еще меньше. При использовании таких генераторов нужно быть чрезвычайно осторожным. Лучше изучить рекомендации Д.Кнута, и построить свой генератор, имеющий наперед известный и достаточно большой период.

Литература

Популярные лекции по математике 1968. Выпуск 46. Соболь И.М. Метод Монте-Карло. М.: Наука, 1968. — 64 с.

Источник: habr.com

Метод Монте Карло – что это в экономике, примеры

Финансовая грамотность

Метод Монте Карло используется для решения различных задач, где результат зависит от случайных процессов. В частности, метод широко используется в экономике, инвестиционных прогнозах и инвестиционном анализе, финансовом планировании. Моделирование по методу Монте Карло позволяет вычислить множество значений. Используя эти значения, определяется искомый результат путем вычисления среднего арифметического или диапазон, в котором может находиться нужный результат.

В этой статье мы расскажем, как применяется метод Монте Карло в экономике, личных финансах и инвестировании. С помощью наглядных примеров попытаемся понять, какие задачи можно решать с применением метода Монте Карло.

Что такое метод Монте Карло (ММК)

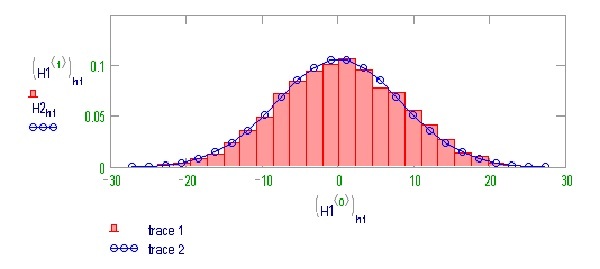
Итак, метод Монте Карло позволяет рассчитать какую-либо величину (или диапазон значений) с использованием множества случайных величин.

К примеру, бегун способен пробежать дистанцию в 10 км за 50 мин. Означает ли это, что 20 км он пробежит за 1 час 40 минут? Конечно же, нет: человек – не машина. Если 10 км можно пробежать без остановки, то расстояние вдвое больше требует значительных затрат энергии. Так, необходимо замедлиться, чтобы попить воды, завязать шнурки.

При сильном учащении пульса – перейти на шаг или легкий бег и т.д.

Таким образом, прогнозирование времени путем простых математических расчетов – способ, который даст весьма неточный результат. Правильнее будет отобрать в случайном порядке результаты забегов нескольких спортсменов (чем больше, тем лучше) такого же пола, примерно того же возраста и уровня подготовки, которые несколько раз бежали дистанции по 20 км, и вычислить среднее арифметическое результатов. Тогда мы получим значение, на которое можно ориентироваться.

Примерно так работает метод Монте Карло простыми словами. С помощью метода можно вычислять риски. Возвращаясь к нашему примеру, подумаем, какова вероятность того, что спортсмен не пробежит 20 км? Причин может быть масса: внезапная травма, сильная усталость, ситуация на дороге и т.д.

Это те самые случайные события, определить вероятность которых невозможно, т.к. они все разные по своей природе. Если все же пользоваться какими-то примерными цифрами или диапазонами значений, то, скорее всего, мы получим такой результат, о котором математики говорят: «задача не имеет решений».

Поэтому следует ориентироваться только на имеющиеся данные, полученные в результате коллективных забегов, когда имели место подобные случаи. Выбрав несколько результатов и сопоставив их с количеством бегунов, пробежавших дистанцию успешно, мы получим средний процент риска.

Для прогнозирования рисков, доходности, сроков окупаемости и других финансовых результатов используется метод Монте-Карло-симуляции. Вероятность события определяется так: программа выбирает комбинации случайных значений (например, неблагоприятных исходов) и на основании этого выдает усредненный результат. Для получения более точного значения симуляцию следует повторить несколько раз. Программное обеспечение применяется различное – от знакомого нам всем Excel до узкоспециализированных программных продуктов, используемых финансовыми аналитиками, физиками, программистами, трейдерами и др.

История

Откуда метод получил свое название? В Европе есть маленькое княжество Монако, где одна из территорий названа Монте-Карло. Это такой европейский Лос-Анджелес, где можно окунуться в роскошь и азартные развлечения. От знаменитого казино метод Монте-Карло получил свое имя.

Впервые о методе заговорили в конце 40-х годов прошлого столетия, когда ВВС США начало разработку водородной бомбы. Тогда, с появлением первых ЭВМ, было предложено использовать теорию вероятностей для решения прикладных задач.

Далее, в 1970-х годах, метод получил применение в нейтронной физике для задач, не поддающихся решению традиционными математическими методами. Впоследствии моделирование по методу Монте-Карло распространилось на другие области физики, а также на экономику и вычислительную математику.

Схема метода

Имитационное моделирование по методу Монте-Карло представляет собой определение математического ожидания (среднего значения случайной величины) путем проведения определенного количества симуляций (испытаний).

Предположим, требуется найти математическое ожидание α для случайной величины ​ ( X ) ​:

Классическая формула расчета математического ожидания выглядит так:

​ ( x1…n ) ​ – значение величины от 1 до n;

​ ( p1…n ) ​ – вероятность от 1 до n.

Моделирование методом Монте-Карло выполняется следующим образом: проводится n симуляций (испытаний). В результате получится какое-то количество значений X. Далее определяется их среднее арифметическое, которое и будет приблизительным значением α.

Зачем нужен ММК и где он применяется

Чтобы не углубляться в математические дебри, сформулируем кратко суть метода.

Метод Монте-Карло относится к методам моделирования различных явлений, событий, параметров или процессов, как благоприятных, так и неблагоприятных, с целью определения вероятности их наступления. Для этого генерируется определенное количество случайных величин, отвечающих установленным критериям, а затем на их основе вычисляют приблизительное значение искомой величины.

ММК применяется в следующих областях:

1. Физика, химия, биология – для моделирования различных явлений.
2. Экономика и финансы – для оценки и прогнозирования инвестиций, расчета доходности финансовых инструментов, сроков окупаемости и др. Метод Монте-Карло широко применяется для оценки рисков;
3. Игровая индустрия – для моделирования искусственного интеллекта и др.
4. Технология и др. инженерные науки используют метод Монте-Карло в прогнозировании НТП.
5. Социология – для изучения общественного мнения (люди, принимающие участие в опросах, отбираются в случайном порядке).

По сути, методу можно найти применение во многих сферах, где необходимы расчеты и прогнозирование.

Входные данные

Данные для получения искомой величины определяются путем стохастической (случайной) выборки. Чтобы было более понятно, приведем простейший пример из компьютерных игр.

Предположим, у нас есть компьютерная игра, в которую мы играли много-много раз. При этом ведется статистика: сыграно 100 игр, из них 30 побед, 70 поражений. Это и будет нашими входными данными. А решение будет таким: вероятность победы – 30%, проигрыша – 70%.

Можно использовать метод Монте-Карло для симуляции инвестиционного портфеля. Предположим, нам нужно получить доходность не менее 10%. Для этого подбираем инструменты с доходностью не меньше этой величины и вычисляем среднее арифметическое. Составляющие портфеля можно варьировать для получения максимальной доходности. Здесь входными данными будут наименование, стоимость и доходность отдельного инструмента, а искомым значением – общая доходность портфеля.

Процесс моделирования методом Монте-Карло

Имитационное моделирование методом Монте-Карло – это автоматизированный процесс, позволяющий рассматривать вероятность наступления различных событий. Каждая смоделированная ситуация является уникальной, что дает возможность оценить целый спектр рисков.

При создании модели все неопределенные факторы заменяются диапазоном возможных значений. К примеру, ни один аналитик, занимающийся оценкой рисков, не может знать, каким будет курс евро через 3-5 лет. Программа позволяет задать диапазон значений на усмотрение специалиста. Разумеется, здесь многое зависит от человека: требуется определенный уровень квалификации.

Далее система распределяет вероятности. Для оценки различных параметров применяются варианты распределения:

• Нормальное распределение. Кривая нормального распределения или Гауссова кривая, выглядит так:

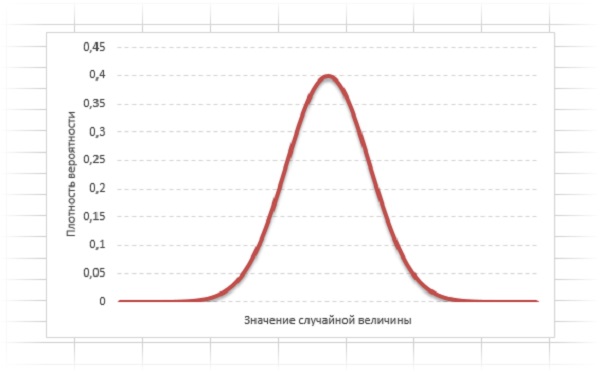
Значение случайной величины, расположенное посередине, характеризует наиболее высокую вероятность. Для построения кривой используются статистические данные: ожидаемое значение и стандартное отклонение. Такой вариант распределения подойдет, к примеру, для расчета стоимости коммунальных услуг в обозримом будущем.

• Равномерное распределение. Все события могут наступить с одинаковой вероятностью, пользователю требуется лишь установить минимум и максимум.

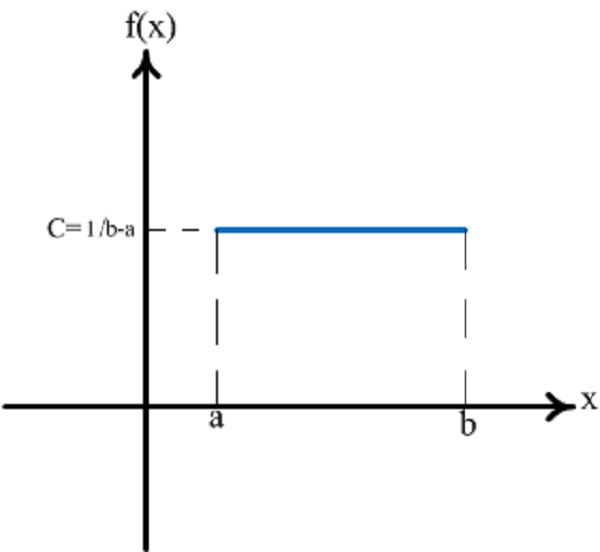
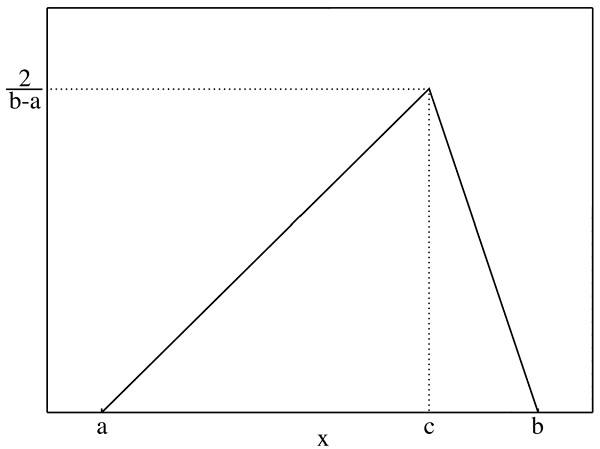
Кривая равномерного распределения имеет вид прямоугольника. На графике a и b – минимальные значения, С – вероятность. Подойдет для расчета условно-постоянных расходов в краткосрочном периоде.

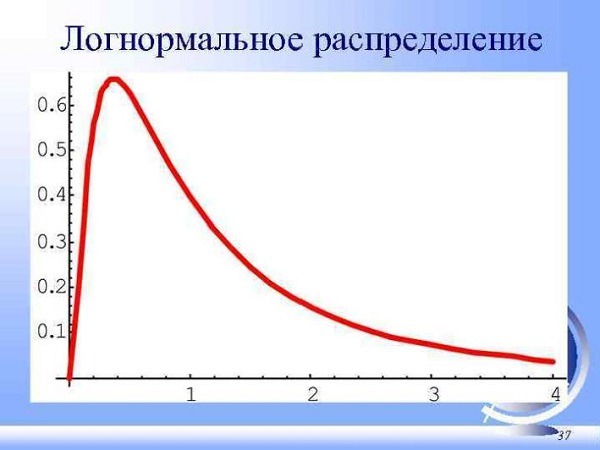
• Логнормальное распределение. Используется для расчета параметров, которые не могут принимать отрицательное значение, но могут расти до бесконечности. Пример: цены на энергоносители. График логнормального распределения выглядит несимметричным.

• Дискретное распределение. Может применяться, к примеру, для компьютерных игр, где вычисляется процент побед и поражений. Пользователю требуется вычислить нужные значения из числа возможных.
• Треугольное распределение. Определяются точки минимума, максимума и максимальной вероятности. Значения, близкие к точке максимальной вероятности, принимаются в качестве вероятных. Этот вариант применяется для анализа продаж, котировок ценных бумаг, прогноза финансовых результатов по итогам деятельности и др. Треугольное распределение подходит для имитационного моделирования рисков по методу Монте-Карло.

Итак, имитационное моделирование по методу Монте-Карло выполняется многократно. По результатам всех операций делается выборка значений, результаты систематизируются и определяется итоговая вероятность события.

Выходные данные

Выходными или итоговыми данными имитационного моделирования по методу Монте-Карло могут быть числовые значения или проценты. В отдельных случаях значения могут находиться внутри диапазона.

Однако итоги тестирования выражаются не только в цифрах. Возможно также выявление каких-то функций или параметров в модели, которые оказывают наибольшее влияние на результат. К примеру, наибольшее влияние на курс рубля оказывают цены на нефть на мировом рынке.

Сколько имитационных испытаний необходимо выполнить

Количество симуляций зависит от цели исследования. Как уже упоминалось, моделирование повторяется сотни, тысячи, иногда десятки тысяч раз – чем больше испытаний, тем более достоверный результат будет получен на выходе. При наличии программы не возникает проблем в многократном повторении операции.

Преимущества и недостатки метода

Достоинствами ММК являются:

1. Простота и универсальность – метод может применяться практически к любому типу данных.
2. ММК позволяет учитывать не только определенный тип данных в отдельности, но и взаимосвязи между различными типами данных.
3. Метод можно применять там, где не срабатывают привычные методы исследования, основанные на математических расчетах.

1. Иногда требуется проведение большого количества испытаний, что может занять много времени.
2. Для выполнения симуляций по методу Монте-Карло в программе необходимо привлекать квалифицированных специалистов.
3. Метод не может дать достоверную оценку для событий, характеризующихся очень низкой или очень высокой вероятностью наступления.

Примеры

Перейдем к практическим примерам использования метода Монте-Карло.

Пример 1. Рассмотрим ситуацию, когда 35-летний человек планирует уйти на пенсию в 60 лет.

• планируемый ежемесячный размер пенсии – 75 000 руб. (1 000 $ или 29 000 грн.) ;
• безопасная ставка снятия (SWR) – 4%;
• ожидаемая доходность инвестиционного портфеля – 6%;
• ожидаемая волатильность портфеля – 15%;
• период для симуляции – 25 лет;
• количество симуляций – 5000.

Таким образом, цель – накопить 300000$ (1000х12/0.04). Проверим вероятность этой суммы, используя симулятор. Программа выполнит 125000 симуляций (5000х25 лет).

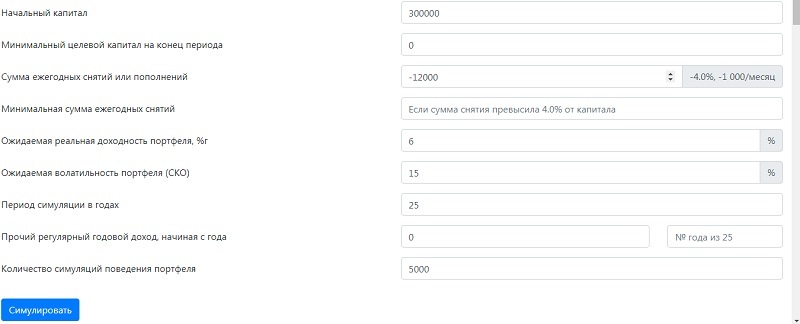
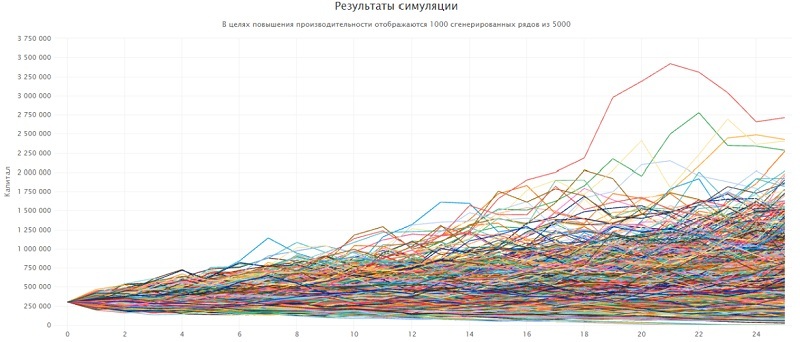
Итак, по первой строчке мы видим, что в 99,7% симуляций цель будет выполнена.

Пример 2. При тех же условиях зададим размер капитала, который мы планируем сохранить на конец периода. Для удобства примем эту сумму равной размеру начального капитала.

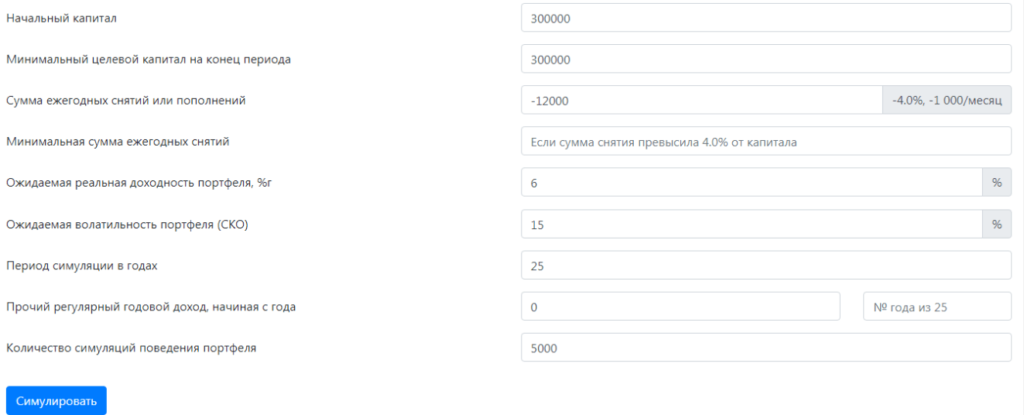
Здесь процент вероятности благоприятного развития событий уменьшился до 84,3%. Что с этим можно сделать?

В какие-то периоды, когда ситуация на рынке оставляет желать лучшего или не возникает крупных непредвиденных расходов, инвестор может снимать со счета меньшую сумму – не 900 000 руб. (12 000 $ или 348 000 грн.) в год, а, скажем, 525 000 руб. (7 000 $ или 203 000 грн.) – 600 000 руб. (8 000 $ или 232 000 грн.) . Кроме того, существует еще и государственная пенсия, которая индексируется на размер инфляционного процента.

Когда я смогу накопить

Метод Монте-Карло является примером подхода к моделированию на основе результатов анализа взаимосвязей между явлениями. В наших примерах эту взаимосвязь можно охарактеризовать так: доходность инвестиций → инфляция → волатильность портфеля → капитал.

Не стоит забывать и о том, что в любую модель могут вноситься коррективы под влиянием воли человека. Причиной тому могут быть непредвиденные обстоятельства, которые случаются в жизни каждого, а уж за анализируемый нам 25-летний период их будет немало. Тем не менее, рассмотрим «обратный» пример, где цель – не сохранить, а наоборот, накопить тот самый капитал в 300000$, необходимый для того, чтобы обеспечить безбедную старость.

• начальный капитал – 1 500 000 руб. (20 000 $ или 580 000 грн.) ;
• планируемая (ожидаемая) сумма ежегодных пополнений счета – 1 125 000 руб. (15 000 $ или 435 000 грн.) ;
• размер прочего регулярного дохода – 900 000 руб. (12 000 $ или 348 000 грн.) в год;
• период симуляции (максимальный срок для накопления капитала) – 20 лет.

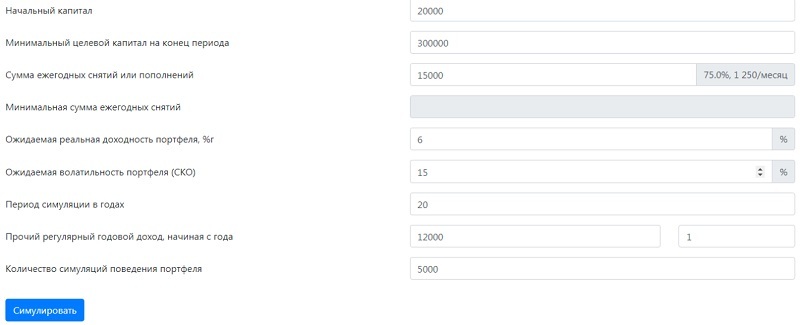
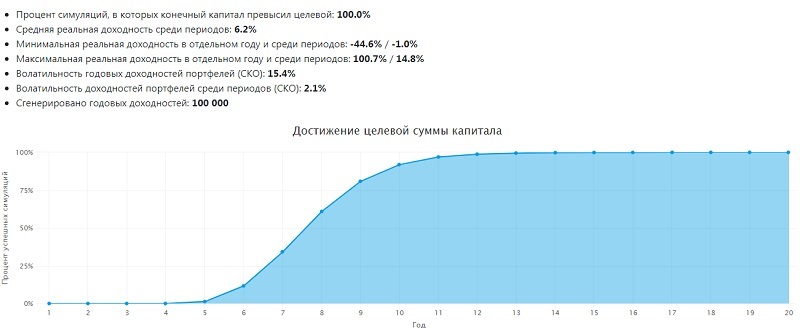
Из графика видно, что нужная сумма накопится примерно на 13-м году. Не следует забывать о падениях рынка, которые случаются раз в несколько лет. Вместе с тем, некоторые активы могут взлететь в цене, что принесет крупный незапланированный доход. Но ориентироваться лучше на срок с запасом в 2-3 года, т.е. примерно 15-16 лет с точки отсчета.

Заключение