Метод гаусса алгоритм программа

Статья посвящена реализации алгоритма Гаусса для решения системы линейных алгебраических уравнений на языке Java.

Теоретические сведения

Рассмотрим математическую теорию. Система линейных уравнений может иметь одно решение, бесконечно много решений или же быть несовместной (не иметь решений). Не все методы решения СЛАУ могут справится с вторым случаем, когда система имеет бесконечно много решений. Например, метод Крамера и матричный метод не применимы, но метод Гаусса вполне можно использовать.

Алгоритм можно условно разделить на два этапа:

• Прямой ход
• Обратный ход

Реализация

Начнем с постановки задачи:

• нам нужно создать программу, реализующую систему линейных уравнений в виде некоторой структуры данных, используя приемы обобщенного программирования. Система должна содержать коэффициенты производного типа от класса Number (т.е. Float, Integer, Double и т.д.)
• Запрограммировать алгоритм, который получив на вход структуру данных системы образует нули ниже главной диагонали

package gauss; public interface Gauss>

Здесь все должно быть ясно, N некоторый наследник Number’а, T — некоторый тип, реализующий данный интерфейс (рекурсивные дженерики). Метод addEquation(T item) позволяет прибавить каждый элемент уравнения item к каждому своему элементу. Остальные методы работают аналогично.

Лекция 150: Идея реализация метода Гаусса на C/C++

Теперь рассмотрим класс системы уравнений. Как видно в листинге ниже, он дженеризирован так же, как и интерфейс Gauss и содержит методы для удобного доступа к приватному списку содержащих в себе уравнений.

package gauss; import java.util.ArrayList; import java.util.List; public class LinearSystem> < private Listlist = new ArrayList(); public T get(int index) < return list.get(index); >public void push(T elem) < list.add(elem); >public int size() < return list.size(); >public N itemAt(int i, int j) < return list.get(i).at(j); >>

Теперь можно приступать к реализации «частного случая» структуры уравнения. Создадим класс MyEquation, реализующий наш интерфейс. Пусть наследником Number’а будет сверхточный класс Float (на практике лучше брать Double). Обратите внимание, что в методе addEquation(MyEquation item) используется объект класса ListIterator, позволяющий изменять элементы перебираемого списка.

Теперь имеем полноценную структуру данных, реализующую систему уравнений. Составим алгоритм который будет принимать некоторый объект, реализующий интерфейс Gauss, затем вызывая нужные методы приведет матрицу к нужному виду.

package gauss; public class Algorithm> < LinearSystemlist = null; public Algorithm(LinearSystem system) < list = system; >public void calculate() throws NullPointerException, ArithmeticException < if (list == null)< throw new NullPointerException(«LinearSysteminstance equal null»); > if (!checkSystem(list)) < throw new ArithmeticException(«Incorrect system for Gauss Method»); >for(int i = 0; i < list.size() — 1; i++)< for(int j = i + 1; j < list.size(); j++)< N k = list.get(j).findCoefficient(list.get(j).at(i), list.get(i).at(i)); list.get(j).mul(k); list.get(j).addEquation(list.get(i)); >> > private boolean checkSystem(LinearSystem system) < if (system.size() < 2) return false; for(int i = 0; i < system.size(); i++)< if (system.get(i).size() != (system.size() + 1))< return false; >> return true; > >

Алгоритм простой, найти нужный коэффициент, домножить на него i-ю строку (i=0..n-1), и прибавить ее к j-й строке (j=i..n). Заметьте, алгоритм не знает как именно реализуются методы findCoefficient, mul и addEquation, это придает коду бОльшую гибкость, т.к. при потребности изменить способы манипуляции уравнениями (строками), будут изменены только реализации трех вышеупомянутых методов, а главный алгоритм останется нетронутым.

VB.net Vs С++. СЛАУ Метод Гаусса

Почти все. Осталось запустить это все в методе main:

import gauss.Algorithm; import gauss.MyEquation; import gauss.LinearSystem; public class Main < private static final int DEFAULT_EQUATIONS_NUMBER = 2; private static final int DEFAULT_VARIABLES_NUMBER = 2; public static void main(String args[])< LinearSystemlist = generateSystem(); printSystem(list); int i, j; Algorithm alg = new Algorithm(list); try< alg.calculate(); >catch (NullPointerException e)< System.out.println(e.getMessage()); System.exit(0); >catch (ArithmeticException e) < System.out.println(e.getMessage()); System.exit(0); >Float [] x = new Float[DEFAULT_EQUATIONS_NUMBER]; for(i = list.size() — 1; i >= 0; i—) < Float sum = 0.0f; for(j = list.size() — 1; j >i; j—) < sum += list.itemAt(i, j) * x[j]; >x[i] = (list.itemAt(i, list.size()) — sum) / list.itemAt(i, j); > printSystem(list); printVector(x); > public static LinearSystem generateSystem() < LinearSystemlist = new LinearSystem(); int i; for (i = 0; i < DEFAULT_EQUATIONS_NUMBER; i++)< MyEquation eq = new MyEquation(); eq.generate(DEFAULT_VARIABLES_NUMBER + 1); list.push(eq); >return list; > public static void printSystem(LinearSystem system) < for (int i = 0; i < system.size(); i++)< MyEquation temp = system.get(i); String s = «»; for (int j = 0; j < temp.size(); j++)< s += String.format(«%f; %s», system.itemAt(i, j), «t»); >System.out.println(s); >System.out.println(«»); > public static void printVector(Float [] x)< String s = «»; for (int i = 0; i < x.length; i++)< s += String.format(«x%d = %f; «, i, x[i]); >System.out.println(s); > >

Запустим это чудо, что бы проверить корректность работы…

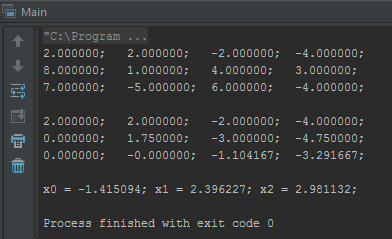
Это все. Исходники можно скачать на github’е.

Вывод

Метод Гаусса не очень поддается обобщенному программированию (как видите обратный ход выполнен отдельно), однако вышла своеобразная реализация которая, надеюсь, поможет кому то лучше разобраться в искусстве использования интерфейсов и дженериков.

Список использованной литературы:

• Математика на доступном языке. Метод Гаусса
• Википедия. Метод Гаусса
• Эквивалентные преобразования матрицы

Источник: habr.com

Программная реализация метода Гаусса

Вычислительная схема метода Гаусса состоит из двух этапов. Первый этап заключается в приведении системы к трапециевидной. Этот этап называется прямым ходом. Второй этап — определение неизвестных — называется обратным ходом.

Прямой ход метода Гаусса состоит в последовательном исключении коэффициентов при неизвестных начиная с первого столбца.

Прямой ход реализуется по следующим формулам (индекс k в круглых скобках означает номер цикла — номер столбца).

Умножение k-й строки на число

Вычитание k-й строки из j-й строки

Обратный ход — вычисление неизвестных — реализуется по следующим формулам, начиная с последнего уравнения системы

Код C++

using namespace std;

cout «Poryadok: » > n;

double **a = new double *[n];

for (i = 0; i new double [n];

double **a1 = new double *[n];

for (i = 0; i new double [n];

double *b = new double [n];

double *x = new double [n];

cout «Vvedite koefficienty i svobodnye chleny » for (i = 1; i for (j = 1; j «a[ » «,» «] margin-left: 120px;»> cin >> a[i][j];

cout «b,[ » «] margin-left: 90px;»> cin >> b[i];

for (k = 1; k // прямой ход

for (j = k + 1; j // формула (1)

for (i = k; i // формула (2)

b[j] = b[j] — d * b[k]; // формула (3)

for (k = n; k >= 1; k—) // обратный ход

for (j = k + 1; j // формула (4)

d = d + s; // формула (4)

x[k] = (b[k] — d) / a[k][k]; // формула (4)

cout «Korni sistemy: » for ( i = 1; i «x[» «] pm2″>» » return 0;

Источник: function-x.ru

Решение систем линейных уравнений методом Гаусса

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Рассмотрим систему линейных уравнений с действительными постоянными коэффициентами:

или в матричной форме

Метод Гаусса решения системы линейных уравнений включает в себя 2 стадии:

• последовательное (прямое) исключение;
• обратная подстановка.

Последовательное исключение

Исключения Гаусса основаны на идее последовательного исключения переменных по одной до тех пор, пока не останется только одно уравнение с одной переменной в левой части. Затем это уравнение решается относительно единственной переменной. Таким образом, систему уравнений приводят к треугольной (ступенчатой) форме. Для этого среди элементов первого столбца матрицы выбирают ненулевой (а чаще максимальный) элемент и перемещают его на крайнее верхнее положение перестановкой строк. Затем нормируют все уравнения, разделив его на коэффициент ai1 , где i – номер столбца.

Затем вычитают получившуюся после перестановки первую строку из остальных строк:

Получают новую систему уравнений, в которой заменены соответствующие коэффициенты.

После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают указанный процесс для всех последующих уравнений пока не останется уравнение с одной неизвестной:

Обратная подстановка

Обратная подстановка предполагает подстановку полученного на предыдущем шаге значения переменной xn в предыдущие уравнения:

Эта процедура повторяется для всех оставшихся решений:

Иллюстрирующий пример

Пусть дана система уравнений

или в матричной форме

Выбираем строку с максимальным коэффициентом ai1 и меняем ее с первой.

Нормируем уравнения относительно коэффициента при x1:


Вычитаем 1 уравнение из 2 и 3:

Выбираем строку с наибольшим коэффициентом при ai2 (уравнение 1 не рассматривается) и перемещаем ее на место 2.

Нормируем 2 и 3 уравнения относительно коэффициента при x2

Вычитаем уравнение 2 из 3

Нормируем уравнение 3 относительно коэффициента при x3

Откуда получаем x3=2 . Подставляем полученное значение в уравнения 2 и 1 получаем

Подставляя полученное значение x2=5 в уравнение 1, найдем

Таким образом, решением системы уравнений будет вектор

Реализация на C++

#include
using namespace std;
// Вывод системы уравнений
void sysout( double **a, double *y, int n)
for ( int i = 0; i < n; i++)
for ( int j = 0; j < n; j++)
cout if (j < n — 1)
cout >
cout >
return ;
>
double * gauss( double **a, double *y, int n)
double *x, max;
int k, index;
const double eps = 0.00001; // точность
x = new double [n];
k = 0;
while (k < n)
// Поиск строки с максимальным a[i][k]
max = abs(a[k][k]);
index = k;
for ( int i = k + 1; i < n; i++)
if (abs(a[i][k]) > max)
max = abs(a[i][k]);
index = i;
>
>
// Перестановка строк
if (max < eps)
// нет ненулевых диагональных элементов
cout cout return 0;
>
for ( int j = 0; j < n; j++)
double temp = a[k][j];
a[k][j] = a[index][j];
a[index][j] = temp;
>
double temp = y[k];
y[k] = y[index];
y[index] = temp;
// Нормализация уравнений
for ( int i = k; i < n; i++)
double temp = a[i][k];
if (abs(temp) < eps) continue; // для нулевого коэффициента пропустить
for ( int j = 0; j < n; j++)
a[i][j] = a[i][j] / temp;
y[i] = y[i] / temp;
if (i == k) continue; // уравнение не вычитать само из себя
for ( int j = 0; j < n; j++)
a[i][j] = a[i][j] — a[k][j];
y[i] = y[i] — y[k];
>
k++;
>
// обратная подстановка
for (k = n — 1; k >= 0; k—)
x[k] = y[k];
for ( int i = 0; i < k; i++)
y[i] = y[i] — a[i][k] * x[k];
>
return x;
>
int main()
double **a, *y, *x;
int n;
system( «chcp 1251» );
system( «cls» );
cout cin >> n;
a = new double *[n];
y = new double [n];
for ( int i = 0; i < n; i++)
a[i] = new double [n];
for ( int j = 0; j < n; j++)
cout cin >> a[i][j];
>
>
for ( int i = 0; i < n; i++)
cout cin >> y[i];
>
sysout(a, y, n);
x = gauss(a, y, n);
for ( int i = 0; i < n; i++)
cout cin.get(); cin.get();
return 0;
>

Результат выполнения

Комментариев к записи: 68

Источник: prog-cpp.ru