1. Объясните, почему следующие предложения не являются высказываниями: • Какого цвета этот дом? • Число X не превосходит единицы. • 4Х +3. • Посмотрите в окно. • Пейте томатный сок! • Эта тема скучна. • Рикки Мартин — самый популярный певец. • Вы были в театре? 2. Объясните, почему формулировка любой теоремы является высказыванием. 3. Приведите по два примера истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.
4. Из данных предложений выберите те, которые являются высказываниями, и обоснуйте свой выбор.
а) Коля спросил: «Который час?» б) Как пройти в библиотеку? в) Картины Пикассо слишком абстрактны. г) Решение задачи — информационный процесс. д) Число 2 является делителем числа 7 в некоторой системе счисления. Решение. Высказываниями являются предложения г) и д), причем высказывание г) — истинно, а д) — ложно.
Предложения а) и б) не являются повествовательными, следовательно, они не являются высказываниями. В предложении в) содержится субъективная оценка, относительно истинности этого предложения сложно сделать какой-либо вывод. Однако если мы договоримся считать, что картины Пикассо слишком абстрактны, то это предложение станет истинным высказыванием.
Разбор варианта уровня ЕГЭ #8 — Информатика 2023
5. Объясните, почему формулировка любой теоремы является высказыванием.
Решение. Все математические теоремы являются утвердительными предложениями. Большинство математических утверждений (теорем) являются высказываниями типа импликации или эквивалентности.
| 4. | Из данных высказываний выберите истинные. |
| а) | Город Джакарта — столица Индонезии. |
| б) | Решение задачи — информационный процесс. |
| в) | Число 2 является делителем числа 7 в некоторой системе счисления. |
| г) | Меню в программе — это список возможных ва риа нтов. |
| д) | Для всех х из области определения выражения x 1 верно, что х + 2 > 0. |
| е) | Сканер — это устройство, которое может напечатать на бумаге то, что |
| изображено на экране компьютера. | |
| ж) | II + VI > VIII. |
| з) | Мышь — устройство ввода информации. |
Ответ. Истинными являются высказывания а), б), г), д) и з).
6. В приведенных предложениях вместо многоточия поставьте подходящие по смыслу слова «необходимо», «достаточно», «необходимо и достаточно». Помните, что получившиеся высказывания должны быть истинными. 1. Для того чтобы число делилось на 4, . чтобы оно было четным.
2. Чтобы число делилось на 3, . чтобы оно делилось на 9. 3. Для того чтобы число делилось на 10, . чтобы оно оканчивалось нулем. 4. Чтобы произведение двух чисел равнялось нулю, . чтобы каждое из них равнялось нулю. Ответы. 1. Необходимо; 2. Достаточно; 3. Необходимо и достаточно; 4. Достаточно.
5. Чтобы произведение двух чисел равнялось нулю, . чтобы хоть одно из них равнялось нулю. 6. Чтобы умножить сумму нескольких чисел на какое-нибудь число, . каждое слагаемое умножить на это число и произведения сложить.
7. Чтобы произведение нескольких чисел разделить на какое-нибудь число, . разделить на это число только один из сомножителей, и полученное частное умножить на остальные сомножители. 8. Для того чтобы сумма двух чисел была числом четным, . чтобы каждое из слагаемых было четным числом. 9. Для того чтобы число делилось на 10, . чтобы оно делилось на 5. 10.
Для того чтобы число делилось на 6, . чтобы оно делилось на 2 и на 3. 11. Для того чтобы число делилось на 12, . чтобы оно делилось на 2 и на 3. 12. Чтобы четырехугольник был квадратом, . чтобы все его стороны были равны. Ответы. 5. Необходимо и достаточно; 6. Достаточно; 7. Достаточно; 8. Достаточно; 9. Необходимо; 10. Необходимо и достаточно; 11.
Необходимо; 12. Необходимо.
Задания для командной работы
Задание 1
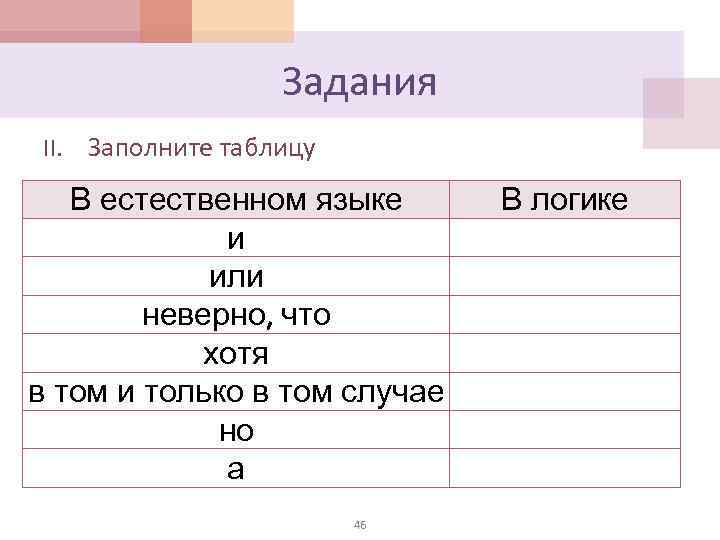
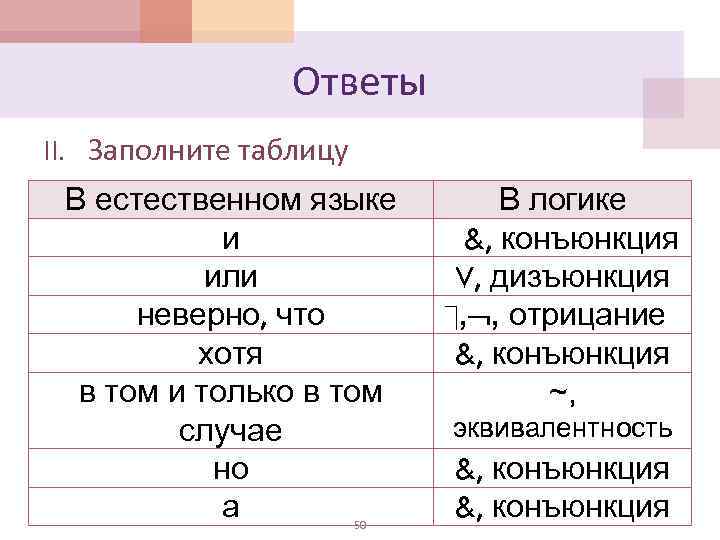
| Этимология названия | Название | Таблица | Соответствующие | Пример высказывания, |
| логической операции | логической | Истинности | операции в теории | построенного с |
| операции | Логической | множеств | Использованием | |
| операции | логической связки | |||
| лат. Inversio — | ||||
| переворачивание | ||||
| лат. Conjunctio — | ||||
| связывание | ||||
| Лат. Disjunctio — | ||||
| разделение | ||||
| лат. Implicatio — | ||||
| переплетение | ||||
| лат. Aequivalens — | ||||
| равноценное |
Задание 2. Формализовать теорему.
Для того чтобы квадратное уравнение имело решение необходимо и достаточно, чтобы дискриминант был неотрицательным. Решение. А = <Квадратное уравнение имеет решение>; В = . Теорема выражается сложным высказываем (через логическую связку эквивалентность) А ~ В.
Задание 3 .
1. В следующих высказываниях выделите простые, обозначив каждое из них буквой; защитите с помощью букв и знаков логических операций каждое составное высказывание. a) Число 376 четное и трехзначное. b) Зимой дети катаются на коньках или на лыжах. c) Новый год мы встретим на даче или на Красной площади. d) Неверно, что Солнце движется вокруг Земли. e) Если сейчас не солнечно, то пасмурно. f) Земля имеет форму шара, который из космоса кажется голубым. g) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу. h) Если вчера было воскресенье, то Дима вчера не был в школе и весь день гулял. i) Если сумма цифр натурального числа делится на 3, то число делится на 3. j) Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3.
Источник: studfile.net
Основные понятия алгебры логики. Логические выражения и логические операции.
Представлена презентация по теме «Основные понятия алгебры логики. Логические выражения и логические операции.» Рассматриваются: основные понятия алгебры логики, подробно представлены логические выражения и логические операции. Учащиеся выполняют ряд упражнеий: определите какие из следующих выражений являются высказываниями, определите какие из следующих выражений являются высказываниями. Учащиеся знакомятся с порядком выполнения логических операций в сложном логическом выражении
Вы уже знаете о суперспособностях современного учителя?
![]()
Тратить минимум сил на подготовку и проведение уроков.
![]()
Быстро и объективно проверять знания учащихся.
![]()
Сделать изучение нового материала максимально понятным.
![]()
Избавить себя от подбора заданий и их проверки после уроков.
![]()
Наладить дисциплину на своих уроках.
![]()
Получить возможность работать творчески.
Просмотр содержимого документа
«Основные понятия алгебры логики. Логические выражения и логические операции.»


Логика (древнегреч. – слово logos ,
означает «мысль, понятие,
рассуждение, закон») — наука о
законах и формах мышления.
Алгебра логики изучает общие
операции над высказываниями.

логики (булева алгебра)
Джорджем Булем в 19

Высказывание (суждение) – это
повествовательное предложение, в
котором что-либо утверждается или
отрицается. По поводу любого
высказывания можно сказать истинно (1)
оно или ложно (0).

- Число 6 – четное.
- Все роботы являются машинами.
- Кто отсутствует?
- Выразите 1 ч 15 мин в секундах.
- А – первая буква в алфавите.

- Треугольник – геометрическая фигура.
- У каждой лошади есть хвост.
- Париж — столица Китая.
- Лед – твердое состояние воды.
- Все люди космонавты.

В алгебре логики высказывания
обозначаются именами логических
переменных (А, В,С), которые могут
Принимать значения истина (1) или
Истина, ложь – логические константы.

Логические выражения бывают
простые или сложные.
Простое логическое выражение
состоит из одного высказывания и не
содержит логические операции. В нём
возможно только два результата –
либо «истина», либо «ложь».

Сл ожное логическое высказывание строится из
простых с помощью связок «И», «ИЛИ», «НЕ»,
которые называются логическими операциями.
Основные логические операции:

Основные понятия Логика высказываний Основные понятия Всякое















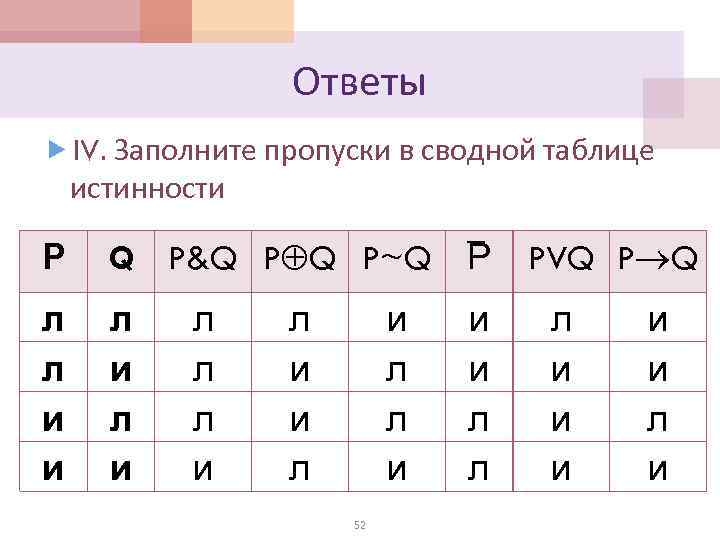
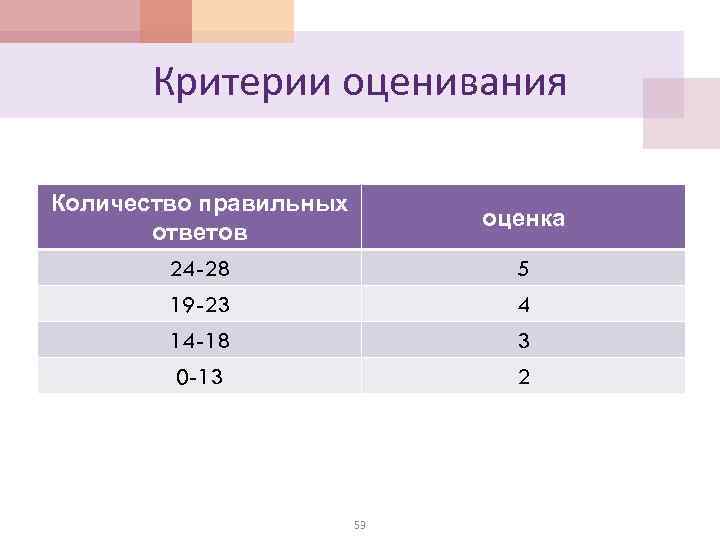

,» />

Источник: present5.com