Matlab simulink описание программы

Попробуем решить его с помощью программы Simulink пакета MATLAB.

Метод решения дифференциальных уравнений отличается от традиционного. Нам необходимо создать схему уравнения. Необходимо будет создать обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp . В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф.

Решение уравнения выглядит так:

Результатом будет график x от y :

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources. Формирует линейный сигнал . В параметрах необходимо задать 1.

Add – Math Operations. В параметрах выбираем необходимые нам операции.

Gain – Math Operations . Коэффициент усиления сигнала. В параметрах ставим значение 3/2.

Sine Wave Function – Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.

Simulink for beginner in MATLAB | getting started with Simulink in MATLAB | Introduction to Simulink

Integrator – Continuous . Выполняет интегрирование входного сигнала.

Scope – Sinks . Выводим результат – график сигнала в функции времени.

Дифференциальные уравнения 2-го порядка.

Дана система уравнений:

Решим ее с помощью программы Simulink пакета MATLAB.

Решаем аналогично предыдущему случаю.

В данной системе уравнений линейно изменяется x от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x . Обязательно надо в интеграторах задать начальные значения y1(0) = 0.1; y2(0) = 0.5.

Результатом будут два графика:

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources . Формирует линейный сигнал. В параметрах необходимо задать все значения 1.

Integrator – Continuous . Выполняет интегрирование входного сигнала. Необходимо задать начальные значения Initial condition для y 1 0.1, для y 2 0.5.

Add – Math Operations . В параметрах выбираем необходимые нам операции.

Divide — Math Operations . Деление первой входной величины на вторую.

Dot Product — Math Operations. Перемножение .

Scope – Sinks. Выводим результат – график сигнала в функции времени.

Решение дифференциального уравнения различными методами, доступными SIMULINK

Страницы работы

1. Решение дифференциального уравнения различными методами, доступными SIMULINK.

Пусть, к примеру, требуется решить линейное дифференциальное уравнение второго порядка с правой частью

При использовании SIMULINK это уравнение можно решить несколькими способами.

Первый способ решения.

а) Разрабатывается блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain раздела Linear. Начнем с того, что разрешим его относительно второй производной

Полученное решение в модулях SIMULINK можно изобразить в виде

Рис. П7.1 Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain[1].

Для решения уравнения нами использованы 2 интегратора, 1 сумматор и 2 усилителя из раздела Linear библиотеки SIMULINK.

Вторая производная, согласно П7.02, должна получится путем вычитания из y0 равного 6/12, производных, умноженных на соответствующие коэффициенты.

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «y(t)».

b) Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения блоков Constant раздела Sources библиотеки SIMULINK и организации решения правой части уравнения в виде подсистемы.

Решение левой части уравнения по-прежнему представим в виде цепочки двух интеграторов, соединенных последовательно.

Для решения правой части уравнения соберем из модулей SIMULINK блок-схему и преобразуем ее в подсистему.

Рис. П7.2. Блок-схема решения правой части уравнения.

Составим блок-схему решения уравнения с использованием подсистемы.

Рис. П7.3. Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Constant[2].

Второй способ решения.

Используя SIMULINK, можно представить другой способ решения этого уравнения. Решение можно получить, используя модуль Transfer Fcn [‘trænsfə: Fkn] (Передаточное звено). В качестве входного сигнала будем использовать блок Constant раздела Sources [so:s — источники]

Рис. П7.4. Решение уравнения с использованием типовых структурных схем[3].

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «Интеграл».

Третий способ решения.

SIMULINK может предложить еще один способ решения данного дифференциального уравнения. Воспользовавшись методами структурных преобразований, данное уравнение можно представить в виде структурной схемы, состоящей из типовых модулей.

Рис. П7.5. Решение уравнения с использованием структурных преобразований[4].

Проведем исследование дифференциального уравнения 2 порядка

методами фазовой плоскости, используя возможности SIMULINK.

Начнем с того, что разрешим уравнение относительно старшей производной.

Решение левой части уравнения представим в виде цепочки из двух интеграторов соответственно настроенных.

Для решения правой части уравнения создадим 2 подсистемы. Одну для формирования значений коэффициентов уравнения, разрешенного относительно старшей производной и вторую для решения собственно правой части уравнения.

Рис. П8.1 Блок-схема формирования коэффициентов уравнения.

Рис. П8.2. Решатель правой части уравнения.

Решение дифференциального уравнения с учетом созданных подсистем будет иметь вид

Рис. П8.3. Блок-схема решения дифференциального уравнения[5].

Исследование фазового портрета.

Для наблюдения за фазовыми траекториями включим в качестве смотрового окна в блок-схему решения уравнения рис. П7.3 дополнительно модуль XY Graph из раздела Sinks библиотеки SIMULINK.

Сущность метода фазовой плоскости заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: ось x — значение исследуемой величины u, ось y – скорость ее изменения du/dt. Процесс изменения траектории представляет собой движение изображающей точки на фазовой плоскости.

Начальные условия определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (x, y) носит название фазовый портрет. Подробнее с методами фазовой плоскости можно ознакомиться по «Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем.

Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. Стр.

485-495».

Задачей нашего исследования является построение некоторых наиболее характерных фазовых портретов.

Рассмотрим следующие случаи характерные для уравнения 2 порядка:

[1] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris1»

[2] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris3»

[3] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris4»

[4] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p7ris5»

[5] Программа расположена на файле «Мои документыПрогSIMПосГлава1gla1_06 p8ris3»

Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

В среде MATLAB можно решать системы диффуров с начальными условиями, краевые задачи, а также решать дифференциальные уравнения в частных производных с помощью инструмента PDE toolbox.

В данном обзоре речь пойдет лишь о системах дифференциальных уравнений с начальными условиями, то есть о задаче Коши. В англоязычной литературе это называется Initial Value Problem.

• каким образом записывать системы диффуров
• как задать начальные условия
• временной интервал
• какой получать результат решения для дальнего использования

Решать системы обыкновенных дифференциальных уравнений можно как в MATLAB, так и в Simulink.

В первую очередь, следует определиться, использовать для решения Matlab и его текстовый редактор, или Simulink, где те же системы дифференциальных уравнений могут быть записаны в виде функциональных блоков.

Выбор ваш должен зависеть от задачи. Если Вы, например, хотите смоделировать какой-либо объект управления, описываемый системой диффуров, то в данном случае имеет смысл использовать именно Simulink, так как Вам, впоследствии, понадобиться синтез, например, системы управления, и Simulink подойдет здесь как нельзя лучше.

А вот если у Вас, например, есть необходимость решать системы диффуров с большим количеством уравнений и неизвестных, или специфика Вашей задачи требует особой и специальной настройки численного метода, а также если вы хотите использовать решение диффура в составе других скриптов MATLAB, то Вам имеет смысл решать дифференциальные уравнения способом, о котором пойдёт речь в этом обзоре.

Рассмотрим синтаксис решателей matlab.В качестве аргументов следует подать правую часть системы в виде MATLAB-функции.

На рисунке показан требуемый вид системы, когда выражены старшие производные.

Системы, чей вид отличается от требуемого, следует преобразовать к таковому.

Если функция простая, то её можно записать прямо в поле аргумента, однако, когда речь идёт о системах уравнений, имеет смысл записывать систему уравнений в виде отдельной функции, в том числе и в виде отдельного м-файла. Об этом мы поговорим чуть позже и на конкретном примере.

Также подается интервал времени, на котором будет найдено решение. Интервал задаётся строкой из двух чисел: начальной величины независимого аргумента t и его конечного значения.

Далее задаются начальные условия. Значения всех неизвестных искомых переменных в начале расчёта задаются в виде столбца соответствующей размерности.

Далее, при необходимости, задаются опции. Вот тут и раскрываются широкие возможности MATLAB по настройке решателя. Помимо управления точностью и величиной шага, имеется возможность обрабатывать данные в процессе вычисления, а также выполнять скрипты по завершению вычисления. Но ещё более полезным является опция отслеживания событий по условию, более подробно поговорим об этом дальше. Также есть другие специальные опции, которые могут быть использованы при решении определённых типов систем.

Вы могли заметить, что название функции — odeXY – это обозначение для всех решателей, которых всего 8 штук. В данном ролике мы пользоваться решателем ode45, соответствующего численному по методу Дормана-Принса 4(5). Этого решателя достаточно для подавляющего большинства задач. Остальные решатели будут подробно рассмотрены в приложении к задачам соответствующих типов позже.

Перейдем к примерам.

Рассмотрим 2 примера:

• решение дифференциального уравнения первого порядка.
• решение системы двух дифференциальных уравнений второго порядка.

В качестве уравнение первого порядка рассмотрим логистическое уравнение Ферхюльста, которое описывает динамику численности популяции. Суть уравнения такова: скорость прироста населения y пропорциональна количеству населения, однако лимитирована максимальной численностью популяции.

Забавный факт: Ферхюльст назвал это уравнение логистическим, и никто до сих пор не знает почему, ибо сам Ферхюльст об этом никому не рассказал.

Решение этого дифференциального уравнения выглядит следующим образом.

Пишем функцию в явном виде, задаём интервал расчёта и записываем начальное условие. Пару слов о записи функции подобным образом. Знак собаки в матлабе является оператором создания функции соответствующих переменных. Вы задаёте аргументы функции и саму функцию через пробел, как показано на рисунке.

Перейдем в окно MATLABа и посмотрим, как это выглядит.

Так выглядит скрипт:

Так выглядит график решения дифференциального уравнения:

В качестве примера решения системы, состоящей из двух дифференциальных уравнений второго порядка, рассмотрим шарик, подвешенный на пружине, который ещё и тормозит о воздух.

Уравнения показаны на рисунке. Но вид системы отличается от требуемого, в том числе потому, что в нём присутствуют вторые производные. Для приведения системы в требуемый вид выполним 2 простых шага:

Первое: следует заменить переменные соответствующим образом. Теперь у нас 4 неизвестных. Далее следует преобразовать уравнение с учетом замены. Таким образом, мы имеем систему из четырёх дифференциальных уравнений первого порядка.

Настало время её записать.

Итак, мы имеем систему, параметры, интервал времени и начальные условия. Решим же эту задачу скорее.

В отличие от предыдущего примера, систему четырех уравнений проблематично записать в поле аргумента. Поэтому всю систему будем записывать в отдельную функцию.

Эту функцию можно располагать как в самом скрипте решения в самом его конце, так и в виде отдельного m-файла.

На выходе функция должна представлять собой вектор-столбец, который записывается перечислением компонент через точку запятой как показано на рисунке.

Теперь рассмотрим скрипт самого решения.

На этот раз запишем интервал и начальные условия в виде переменных MATLAB. Интервал, соответственно, в виде строки, а начальные условия – в виде столбца длинной 4.

Сообразно с уже разобранным ранее синтаксисом укажем функцию pendulum_np, интервал времени и начальные условия.

Перейдем теперь в окно MATLAB и посмотрим решение.

Так выглядит скрипт:

Запускаем скрипт и получаем графики:

Зачастую хочется, чтобы одну и ту же систему можно было бы решать с разными параметрами, и при этом не менять их в теле самой функции. И это можно, и даже нужно осуществлять.

На рисунке показана функция MATLAB, которая соответствует движению подвешенного на пружине шара, однако можно заметить, что эта функция теперь имеет на 5 аргументов больше.

Параметры задаются в скрипте, а при вызове функции мы обращаемся к уже известному оператору-собаке, которая превращает функцию семи переменных pendulum_n в функцию двух переменных t и X. Вот и всё.

Я вам очень рекомендую разобраться с тем, как работает оператор-собака. В хелпе он называется function-handle. Разобравшись с ним Вам будет работать в среде MATLAB ещё проще и ещё приятнее.

Вывод: не так страшно решать диффуры

Под конец стоит сказать какие вообще системы дифференциальных уравнений матлаб может решать, а может он решать системы практически любых типов.

Их можно, с одной стороны, разделить по степени жёсткости, а с другой стороны, по структуре самой системы.

Когда уравнения представляют поведение системы, которая содержит ряд быстрых и медленных реакций, то такую систему уравнения можно назвать жесткой. Для жестких задач явные численные методы работают плохо, или не работают вовсе. Примером жесткой задачи может являться протекание тока через клеточную мембрану. На самом деле, чёткого разделения между жесткими и нежёсткими системами не существует. Степень жесткости системы формально определяется через собственные значения матрицы Якоби, но давайте не будем закапываться.

Видеообзор по теме решения систем Д/У доступен по ссылке.

Источник: al-shell.ru

Simulink

Simulink – среда динамического междисциплинарного моделирования сложных технических систем и основной инструмент для модельно-ориентированного проектирования. Его основным интерфейсом является графический инструмент для построения диаграмм и настраиваемый набор библиотек блоков. Он предлагает тесную интеграцию с остальной средой MATLAB и может либо использовать MATLAB, либо создавать сценарии из него. Simulink широко используется в автоматическом управлении и цифровой обработке сигналов для многодоменного моделирования и проектирования на основе моделей.

В сочетании с другими своими продуктами Simulink может автоматически генерировать исходный код на языке C для реализации систем в режиме реального времени. Поскольку эффективность и гибкость кода улучшаются, он становится все более широко распространенным для производственных систем, в дополнение к тому, что является инструментом для разработки встроенных систем из-за его гибкости и способности к быстрой итерации, Встроенный кодер создает код, достаточно эффективный для использования во встроенных системах.

Simulink. Начало работы

Модельно-ориентированное проектирование: от концепции к коду

Модельно-Ориентированное Проектирование в Simulink

Модельно-Ориентированное Проектирование в Simulink

Simulink предназначен для моделирования и симуляций на системном уровне, что позволяет проводить всестороннее исследование разрабатываемой системы в единой среде проектирования.

Моделирование и симуляции позволяют провести проверку поведения системы в критических условиях или аварийных сценариях. Тем самым происходит снижение затрат на дорогостоящие физические прототипы. Проверка системы осуществляется с помощью полунатурного моделирования и быстрого прототипирования.

Модели Simulink поддерживают автоматическую генерацию кода промышленного качества на языках С, C++ и HDL. Результаты работы сгенерированного кода и модели идентичны. Следующим шагом является развертывание кода на целевом вычислителе или FPGA/ASIC.

Simulink использует преимущества MATLAB

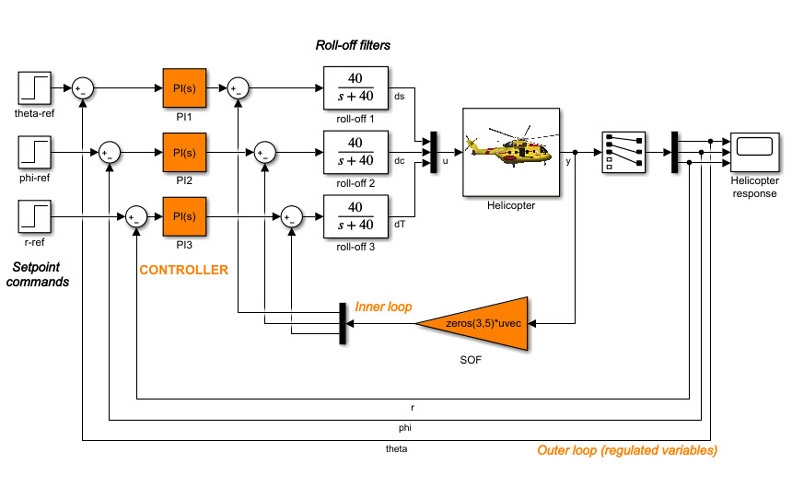
Система управления в Simulink

Алгоритмы, созданные в MATLAB, не требуется переделывать для повторного использования в Simulink. Код MATLAB добавляется в блок Simulink или диаграмму Stateflow без изменений.

Так же MATLAB используется для создания наборов входных данных для симуляций систем. Симуляции масштабируются на кластеры для ускорения таких инженерных задач как перебор параметров или оптимизация, а затем их результаты анализируются и визуализируются в MATLAB.

Система управления в Simulink

Источник: exponenta.ru

Matlab simulink описание программы

Чипинфо MATLAB для DSP. Часть 1. Моделирование аналого-цифрового преобразования

Распродажа

Электронные компоненты со склада по низким ценам, подробнее >>>

2003:

2002:

2001:

2000:

1999:

О журнале ChipNews

Литература

Новости электроники

Популярные материалы

В рамках проекта «MATLAB для DSP» настоящая статья═ первая публикация по наиболее простым и удобным средствам имитационного моделирования, которые предоставляет пакет MATLAB. Речь идет о составной части этого пакета═ программе Simulink. Несмотря на то, что Simulink▓у посвящены обстоятельные разделы в книге по MATLAB [1] и даже отдельная монография [2], представляется полезным на конкретных примерах показать, как возможности Simulink могут быть использованы в задачах построения систем для цифровой обработки сигналов и учебном процессе. Здесь мы следуем известной рекомендации Ньютона: примеры часто бывают поучительнее методов. Читатель, будь то преподаватель, инженер или студент, имеет возможность без труда повторить наши примеры, что побудит использовать MATLAB в практической деятельности.

Каждый, кто занимается цифровой обработкой сигналов, знает, как важно построить математическую модель проектируемого устройства, реализовать ее в виде программы и затем провести на этой модели испытания в условиях, «приближающихся к боевым».

Simulink является мощным средством решения таких задач для разных предметных областей и, может быть, в первую очередь, для задач в области цифровой обработки сигналов. Использование Simulink во многих случаях исключает утомительные и трудоемкие этапы составления и отладки программ, позволяя сосредоточить основные усилия непосредственно на решении «своих» предметно-ориентированных задач. Инженеру или студенту нужно освоить правила использования готовых функциональных блоков, из которых, как из конструктора, составляется модель проектируемого устройства, а также, и это следует особо подчеркнуть, «испытательный стенд», то есть вся необходимая инфраструктура, включающая источники сигналов, измерительные приборы и средства наблюдения за процессами и характеристиками процессов. При этом гарантируется высокое качество «строительного материала», в создании которого использованы опыт и знания ведущих специалистов.

Итак, Simulink═ это интерактивная графическая программа, управляемая мышью, которая позволяет моделировать динамические системы на уровне структурных и функциональных схем. Библиотеки Simulink содержат большое количество разнообразных функциональных блоков, которые отображаются на экране в виде пиктограмм.

В настоящей статье описывается процесс построения простой модели аналого-цифрового преобразователя (АЦП), а также рассматриваются эффекты, связанные с аналого-цифровым преобразованием. В первой части приводятся состав и краткое описание модели, процесс ее построения, а также процедура компоновки модели. Во второй части, которая будет опубликована в «Chip News» ╧ 3, будут приведены процесс построения модели, необходимые сведения о входящих в нее функциональных блоках и результаты моделирования, а также дополнительные возможности по использованию модели.

Описание моделируемой системы

Для того, чтобы продемонстрировать, насколько просто и удобно строить модели устройств и создавать «измерительные стенды» в Simulink, смоделируем простейший АЦП, функциональная схема которого показана на рис.═1. Наша цель═ изучить эффекты аналого-цифрового преобразования. Исходный сигнал с генераторов, расположенных в левой части рисунка, поступает на вход АЦП, моделируемого с помощью последовательно соединенных блоков Zero-Order Hold и Quantizer (на рисунке модель заключена в контур). Осциллографы позволяют наблюдать за исходным сигналом и результатом его преобразования (Scope1), а также за поведением ошибки квантования (Scope).

Рис. 1. Моделирование аналогово-цифрового преобразования сигналов

Блок вычисления гистограмм (Histogram) предна-значен для вычисления, а блок графического отображения (User-defined Frame Scope)═ для построения гистограммы (в нашем случае, ошибки квантования). В рассматриваемой модели блок Histogram формирует векторный выходной сигнал, содержащий число значений входного сигнала, попадающих в заданные интервалы (иногда их называют бины), а блок User-defined Frame Scope строит график, на котором по оси ординат отложены значения этого сигнала, а по оси абцисс═ номера интервалов, называемых интервалами группировки.

Вычисление и отображение дисперсии ошибки выполняется соответственно блоками Variance и Display. Как видно из рисунка, в зависимости от положения переключателя Manual Switch, на входы Rst блоков Variance и Histogram поступают постоянные сигналы, равные либо нулю, либо единице. При поступлении на эти входы ненулевого (в данном случае, равного единице) сигнала, накопленная в блоках информация стирается, и происходит обнуление выходов.

Кроме моделирования во временной области, можно вычислять и графически отображать оценки спектральной плотности мощности (СПМ) исходного и преобразованного сигналов и ошибки квантования. Это выполняется с помощью блоков Buffered FFT Frame Scope и Buffered FFT Frame Scope1, которые вычисляют квадрат амплитуды преобразования Фурье входных данных, накопленных в буфере каждого из блоков, а затем выводят результаты в виде графиков.

Каждый раз после заполнения буфера, вычисления и графического отображения результата происходит очистка буфера, и процесс повторяется. Блоки GainGain2 играют роль масштабирующих множителей (усилителей, аттенюаторов). Таким образом, при моделировании можно наблюдать изменяющуюся СПМ, соответствующую разным выборкам сигналов, взвешенных прямоугольным временным окном. Размер окна совпадает с размером буфера.

Компоновка модели

Перед построением модели необходимо предварительно загрузить систему MATLAB и запустить Simulink. Запуск выполняется из командного окна MAT-LAB, для чего необходимо подвести курсор мыши к кнопке запуска этой программы, находящейся в верхней части окна, и щелкнуть левой клавишей мыши либо набрать в командном окне следующую команду simulink, как показано на рис.═2.

Рис. 2. Командное окно MATLAB и запуск Simulink

В том и другом случае откроется окно Simulink Library Browser (система просмотра библиотек Simulink), изображенное на рис.═3. В верхней части этого окна две крайние левые кнопки служат, соответственно, для создания новой и открытия существующей модели. После нажатия левой кнопки на экране появится окно для построения новой модели. Процесс построения модели АЦП, как впрочем, и любой другой модели Simulink, включает ее компоновку и задание необходимых параметров. Компоновка заключается в выборе из библиотек Simulink необходимых блоков, их размещение в открывшемся окне и соединение между собой.

Рис. 3. Система просмотра библиотек Simulink Library Browser

Поиск и перемещение блоков

Процедура поиска и перемещения блоков из библиотек Simulink в окно модели во многом напоминает операции копирования и перемещения файлов в среде Windows. В частности, технология работы с Simulink Library Browser (рис.═3) аналогична работе с Проводником Windows.

Поместим в окно модели блоки источников сигналов Signal Generator (генератор синусоидальных, прямоугольных, пилообразных и случайных сигналов) и Band-Limited═White═Noise (генератор шума в заданной полосе частот), находящиеся по адресу Simu-linkSources, для чего откроем библиотеку Simulink в окне Simulink Library Browser и находящуюся в ней библиотеку Sources. В результате, окно Simulink Library Browser примет вид, аналогичный показанному на рис.═4 (там также указаны блоки, которые следует переместить в окно модели). Для перемещения курсор мыши устанавливается на нужный блок. Затем, нажав левую клавишу мыши, блок перемещает его в окно модели. Отметим, что, кроме непосредственного просмотра содержимого библиотек, любой блок может быть найден по имени (если оно известно), введенному в текстовое поле, расположенное в правой верхней части Simulink Library Browser (рис.═4).

Рис. 4. Библиотека Sources

• блок выборки и хранения SimulinkDiscreteZero-Order═Hold (то═есть блок Zero-Order═Hold, находящийся в библиотеке SimulinkDiscrete)═ осуществляет выборку мгновенного значения входного сигнала в заданный момент времени и фиксацию его на выходе вплоть до следующего момента выборки;
• квантователь SimulinkNonlinearQuantizer═ выполняет квантование входного сигнала по уровню;
• сумматор SimulinkMathSum (пиктограмма имеет вид кружка со знаками арифметических операций «+» и/или «-«)═ выполняет суммирование входных дискретных сигналов с учетом указанных знаков;
• коэффициент умножения SimulinkMathGain═ выполняет умножение входного сигнала на заданную величину;
• константа SimulinkSourcesConstant═ генерирует постоянную величину;
• ручной переключатель SimulinkNonlinearManual═ Switch═ изменяет свое состояние двойным щелчком левой клавишей мыши;
• мультиплексор SimulinkSignals═
• осциллограф SimulinkSinksScope═ отображает в виде графика входной сигнал;
• цифровой индикатор SimulinkSinksDisplay═ отображает численное значение текущего отсчета входного сигнала;
• блок вычисления дисперсии DSP BlocksetMath FunctionsStatisticsVariance═ вычисляет дисперсию входного сигнала;
• блок вычисления гистограмм DSP BlocksetMath FunctionsStatisticsHistogram═ вычисляет гистограмму для заданного диапазона значений входного сигнала;
• блок графического отображения DSP BlocksetDSP SinksUser-Defined Frame Scope═ позволяет строить графики входных данных, не ограничивая пользователя только временными или частотными зависимостями;
• блок буферизации и вычисления квадрата преобразования Фурье DSP BlocksetDSP SinksBuffered FFT═Frame═Scope═ накапливает в буфере отсчеты входного сигнала, после заполнения буфера вычисляет квадрат преобразования Фурье.

Соединение и дублирование блоков

Для объединения блоков в систему необходимо соединить их входные и выходные порты, которые на пиктограммах блоков отмечены значком «>». В качестве примера на рис.═5 показаны порты блока Gain (коэффициент усиления). Для того, чтобы соединить два блока между собой, надо подвести курсор мыши к порту одного из соединяемых блоков (при этом курсор примет форму крестика, как показано на рис.═6а), нажать левую клавишу мыши и, удерживая ее в нажатом положении, переместить курсор к порту другого блока (курсор примет вид двойного крестика, что отражено на рис. 6б), после чего отпустить удерживаемую клавишу.

Рис. 5. Входные и выходные порты

Рис. 6. Соединение блоков:
а) в этом положении курсора нажать левую клавишу мыши
б)в этом положении курсора отпустить нажатую клавишу

Из рис.═1 видно, что для построения модели требуется по два блока Zero-Order Hold, Scope, Mux, Constant, Buffered FFT Frame Scope, Sum и три блока Gain. Конечно, можно многократно повторять процедуру перемещения одного и того же блока из библиотеки в окно создаваемой модели, однако Simulink позволяет создавать копии (дубликаты) блоков из имеющихся в окне модели.

Для создания копии блока надо установить курсор на требуемый блок в окне модели, нажать на клавиатуре клавишу «Ctrl» и затем левую клавишу мыши. В результате, слева от курсора появится знак «+» (рис.═7а). Затем, удерживая клавиши в нажатом положении, переместить в нужное место курсор и отпустить нажатые клавиши.

При построении модели, как видно из рис.═1, требуется не только соединять блоки между собой, но и делать ответвления от существующих соединительных линий. Например, линия, соединяющая блоки Quantizer и сумматор, имеет ответвление к блоку Gain1. Проведение линии, соединяющей входной порт какого-либо блока с существующей линией, выполняется аналогично дублированию блоков, то═есть при нажатой клавише «Ctrl». Разница лишь в том, что в этом случае курсор мыши устанавливается на линию, от которой проводится ответвление, и перемещается к входному порту соединяемого блока, или наоборот (от входного порта к линии).

Рис. 7. Дублирование блоков:
а) начальное положение курсора и результат нажатия левой клавиши мыши и «CTRL» на клаиатуре;
б)результат перемещения курсора при удерживаемых клавишах

Необходимые программные средства для проекта предоставлены фирмой SoftLine Corp.

1. Дьяконов В.П., Абраменкова И.В. Matlab 5.0/5.3. Система символьной математики. М.: «Нолидж». 1999. 633 с.
2. Гультяев═А.К. Имитационное моделирование в среде Windows. СПб.: КОРОНА принт. 1999. 288═с.
3. Потемкин В.Г. Система MATLAB. Справ. пособие. Диалог-МИФИ. 1997. 350 с.
4. Потемкин В.Г. MATLAB 5 для студентов. Диалог-МИФИ. 1998. 314 с.
5. Потемкин В.Г. MATLAB 5 для студентов. Диалог-МИФИ. 1999. 447 с.
6. Потемкин В.Г. Система инженерных и научных расчетов MATLAB 5.х. В 2-х томах. Диалог-МИФИ. 1999 (т. 1. 366 с., т. 2. 304 с.).
7. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования с примерами на языке МАТЛАБ. Учеб. Пособие под ред. проф. Фрадкова А.Л. СПб: БГТУ. 1994. 190 с.
8. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования. Издание 2 дополненное. СПб: БГТУ. 1996. 191 с.
9. Дьяконов В.П. Справочник по применению системы PC MatLAB. М.: Наука, Физматлит. 1993. 112 с.

Источник: www.chipinfo.ru