Matlab пример работы программы

В этом разделе вы найдете бесплатные примеры решений задач и лабораторных работ, выполненные с применением пакета Matlab. Используйте данные примеры или закажите свою работу профессионалам.

Полезная страница? Сохрани или расскажи друзьям

Решенные задания в Матлаб онлайн

Задача 1. Дано: характеристическое уравнение системы. Задание: определить область устойчивости по заданному параметру.

Задача 2. Определение коэффициентов однопараметрических моделей технологических процессов статистическими методами
В данной работе по экспериментальным данным, полученным на промышленных технологических установках ректификации, дегидрирования углеводов, сушки и т. д., необходимо выработать вид однопараметрической линии регрессии, определить параметры и оценить адекватность предложенной регрессионной модели реальному процессу.

Лабораторная работа №1. Матричные преобразования и трехмерная графика в Matlab
Цель работы: освоение специфики матричных преобразований Matlab и сравнительный анализ различных форм графического отображения результатов.

MATLAB 03 Написание программ

Лабораторная работа №2. МОТС
1) Найти $E, sigma, sigma^2$, построить гистограмму $w(t)$ для сигналов
— Моногармонический: $s=sin(2 pi f t)$
— C линейной частотой модуляцией: $s=sin(2 pi f t^2)$
— С амплитудной модуляцией: $s=sin(2pi f_n t)*(1+ m*sin(2pi f_c t))$, где
$f_n$ – несущая частота, $f_c$ – частота сигнала, $m$ – глубина модуляции
— С частотной модуляцией: $s=sin(2pi f_c(t) t)$
— С фазовой модуляцией: $s=sin(2pi f_n t+phi(t))$
При создании сигналов задать количество точек 10000. Построить график зависимости $sigma, sigma^2$ от выбора интервала осреднения (т.е. выбирая разное количество точек для расчета).
2) Для сигналов из п.1 построить АКФ и спектр. Получить преобразование Фурье от АКФ, сравнить со спектром 3) Измерение высоты полета самолета.
— создать сигнал [1 1 …1 0 0 …. 0]
— создать его сдвинутую копию
— добавить шум (randn(1,N)), оценить отношение сигнал/шум $(20*log10(sigma_c/sigma_q))$
— построить КФ
— повторить с разной реализацией шума, фиксируя положения максимума (max)
— повторить для разного отношения сигнал/шум
Повторить для 2 сигналов из п.1

Задача 5. Дана структурная схема (см. файл):
1. Рассчитать передаточную функцию по возмущению:
$$W_p(s)=frac, W_0(s)=frac$$ $$W_p(s)=frac, W_0(s)=frac$$ 2. Построить переходные характеристики каждой из систем в Matlab Simulink, и по переходной характеристике определить ошибку.

Задача 6. Вычислите значения функции $f(x)=x^2/(1+0.25sqrt(x))$ на отрезке $[a; b]=[1.1; 3.1]$ с шагом $h=0.2$.

Источник: www.matburo.ru

Глава 3. Работа с графиками в MatLab

MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое.

MATLAB 01 Начало работы

Функция plot

Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах.

Предположим, что требуется вывести график функции синуса в диапазоне от 0 до . Для этого зададим вектор (множество) точек по оси Ox, в которых будут отображаться значения функции синуса:

В результате получится вектор столбец со множеством значений от 0 до и с шагом 0,01. Затем, вычислим множество значений функции синуса в этих точках:

и выведем результат на экран

В результате получим график, представленный на рис. 3.1.

Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика.

Рис. 3.1. Отображение функции синуса с помощью функции plot().

Функцию plot() можно записать и с одним аргументом x или y:

в результате получим два разных графика, представленные на рис. 3.2.

Анализ рис. 3.2 показывает, что в случае одного аргумента функция plot() отображает множество точек по оси Oy, а по оси Оx происходит автоматическая генерация множества точек с единичным шагом. Следовательно, для простой визуализации вектора в виде двумерного графика достаточно воспользоваться функцией plot() с одним аргументом.

Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом:

x = 0:0.01:pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2);

Результат работы данного фрагмента программы представлен на рис. 3.3.

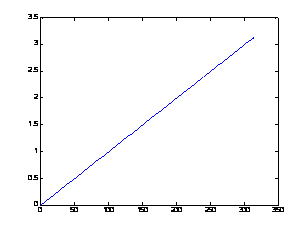
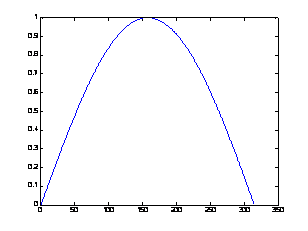
Рис. 3.2. Результаты работы функции plot() с одним аргументом:

а – plot(x); б – plot(y).

Рис. 3.3. Отображение двух графиков в одних координатных осях.

Аналогичным образом можно построить два графика, используя один аргумент функции plot(). Предположим, что есть два вектора значений

y1 = sin(x);
y2 = cos(x);

которые требуется отобразить на экране. Для этого объединим их в двумерную матрицу

в которой столбцы составлены из векторов y1 и y2 соответственно. Такая матрица будет отображена функцией

plot([y1’ y2’]); % апострофы переводят вектор-строку
% в вектор-столбец

в виде двух графиков (рис. 3.4).

Рис. 3.4. Отображение двумерной матрицы в виде двух графиков.

Два вектора в одних осях можно отобразить только в том случае, если их размерности совпадают. Когда же выполняется работа с векторами разных размерностей, то они либо должны быть приведены друг к другу по числу элементов, либо отображены на разных графиках. Отобразить графики в разных координатных осях можно несколькими способами. В самом простом случае можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом:

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

plot(x1, y1); % рисование первого графика
figure; % создание 2-го графического окна
plot(x2, y2); % рисование 2-го графика во 2-м окне

Функция figure, используемая в данной программе, создает новое графическое окно и делает его активным. Функция plot(), вызываемая сразу после функции figure, отобразит график в текущем активном графическом окне. В результате на экране будут показаны два окна с двумя графиками.

Неудобство работы приведенного фрагмента программы заключается в том, что повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. В этом случае было бы лучше построить программу так, чтобы на экране всегда отображалось два окна с нужными графиками. Этого можно достичь, если при вызове функции figure в качестве аргумента указывать номер графического окна, которое необходимо создать или сделать активным, если оно уже создано. Таким образом, вышеприведенную программу можно записать так.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1); %создание окна с номером 1
plot(x1, y1); % рисование первого графика
figure(2); % создание графического окна с номером 2
plot(x2, y2); % рисование 2-го графика во 2-м окне

При выполнении данной программы на экране всегда будут отображены только два графических окна с номерами 1 и 2, и в них показаны графики функций синуса и косинуса соответственно.

В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис:

Рассмотрим пример отображения двух графиков друг под другом вышеприведенных функций синуса и косинуса.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1);
subplot(2,1,1); % делим окно на 2 строки и один столбец
plot(x1,y1); % отображение первого графика
subplot(2,1,2); % строим 2-ю координатную ось
plot(x2,y2); % отображаем 2-й график в новых осях

Результат работы программы показан на рис. 3.5.

Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Для этого используется параметр position в функции subplot():

subplot(‘position’, [left bottom width height]);

где left – смещение от левой стороны окна; bottom – смещение от нижней стороны окна; width, height – ширина и высота графика в окне. Все эти переменные изменяются в пределах от 0 до 1.

Рис. 3.5. Пример работы функции subplot.

Ниже представлен фрагмент программы отображения графика функции синуса в центре графического окна. Результат работы показан на рис. 3.6.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

subplot(‘position’, [0.33 0.33 0.33 0.33]);
plot(x1,y1);

В данном примере функция subplot() смещает график на треть от левой и нижней границ окна и рисует график с шириной и высотой в треть графического окна. В результате, получается эффект рисования функции синуса по центру основного окна.

Таким образом, используя параметр position можно произвольно размещать графические элементы в плоскости окна.

Рис. 3.6. Пример работы функции subplot с параметром position.

Оформление графиков

Пакет MatLab позволяет отображать графики с разным цветом и типом линий, показывать или скрывать сетку на графике, выполнять подпись осей и графика в целом, создавать легенду и многое другое. В данном параграфе рассмотрим наиболее важные функции, позволяющие делать такие оформления на примере двумерных графиков.

Функция plot() позволяет менять цвет и тип отображаемой линии. Для этого, используются дополнительные параметры, которые записываются следующим образом:

Обратите внимание, что третий параметр записывается в апострофах и имеет обозначения, приведенные в таблицах 3.1-3.3. Маркеры, указанные ниже записываются подряд друг за другом, например,

‘ko’ – на графике отображает черными кружками точки графика,
‘ko-‘ – рисует график черной линией и проставляет точки в виде кружков.

Табл. 3.1. Обозначение цвета линии графика

Маркер	Цвет линии
c	голубой
m	фиолетовый
y	желтый
r	красный
g	зеленый
b	синий
w	белый
k	черный

Табл. 3.2. Обозначение типа линии графика

Маркер	Цвет линии
—	непрерывная
—	штриховая
:	пунктирная
-.	штрих-пунктирная

Табл. 3.3. Обозначение типа точек графика

Маркер	Цвет линии
.	точка
+	плюс
*	звездочка
o	кружок
x	крестик

Ниже показаны примеры записи функции plot() с разным набором маркеров.

x = 0:0.1:2*pi;
y = sin(x);

subplot(2,2,1); plot(x,y,’r-‘);
subplot(2,2,2); plot(x,y,’r-‘,x,y,’ko’);
subplot(2,2,3); plot(y,’b—‘);
subplot(2,2,4); plot(y,’b—+’);

Результат работы фрагмента программы приведен на рис. 3.7. Представленный пример показывает, каким образом можно комбинировать маркеры для достижения требуемого результата. А на рис. 3.7 наглядно видно к каким визуальным эффектам приводят разные маркеры, используемые в программе.

Следует особо отметить, что в четвертой строчке программы по сути отображаются два графика: первый рисуется красным цветом и непрерывной линией, а второй черными кружками заданных точек графика. Остальные варианты записи маркеров очевидны.

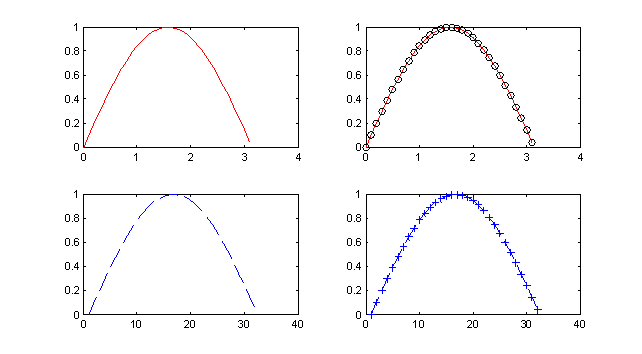
Рис. 3.7. Примеры отображения графиков с разными типами маркеров

Из примеров рис. 3.7 видно, что масштаб графиков по оси Ox несколько больше реальных значений. Дело в том, что система MatLab автоматически масштабирует систему координат для полного представления данных. Однако такая автоматическая настройка не всегда может удовлетворять интересам пользователя. Иногда требуется выделить отдельный фрагмент графика и только его показать целиком. Для этого используется функция axis() языка MatLab, которая имеет следующий синтаксис:

axis( [ xmin, xmax, ymin, ymax ] ),

где название указанных параметров говорят сами за себя.

Воспользуемся данной функцией для отображения графика функции синуса в пределах от 0 до :

x = 0:0.1:2*pi;
y = sin(x);

subplot(1,2,1);
plot(x,y);
axis([0 2*pi -1 1]);

subplot(1,2,2);
plot(x,y);
axis([0 pi 0 1]);

Из результата работы программы (рис. 3.8) видно, что несмотря на то, что функция синуса задана в диапазоне от 0 до

, с помощью функции axis() можно отобразить как весь график, так и его фрагмент в пределах от 0 до .

Рис. 3.8. Пример работы функции axis()

В заключении данного параграфа рассмотрим возможности создания подписей графиков, осей и отображения сетки на графике. Для этого используются функции языка MatLab, перечисленные в табл. 3.4.

Таблица 3.4. Функции оформления графиков

Название	Описание
grid [on, off]	Включает/выключает сетку на графике
title(‘заголовок графика’)	Создает надпись заголовка графика
xlabel(‘подпись оси Ox’)	Создает подпись оси Ox
ylabel(‘подпись оси Oy’)	Создает подпись оси Oy
text(x,y,’текст’)	Создает текстовую надпись в координатах (x,y).

Рассмотрим работу данных функций в следующем примере:

x = 0:0.1:2*pi;
y = sin(x);

plot(x,y);
axis([0 2*pi -1 1]);
grid on;
title(‘The graphic of sin(x) function’);
xlabel(‘The coordinate of Ox’);
ylabel(‘The coordinate of Oy’);
text(3.05,0.16,’leftarrow sin(x)’);

Из результата работы данной программы, представленного на рис. 3.9, видно каким образом работают функции создания подписей на графике, а также отображение сетки графика.

Таким образом, используя описанный набор функций и параметров, можно достичь желаемого способа оформления графиков в системе MatLab.

Рис. 3.9. Пример работы функций оформления графика

Источник: megaobuchalka.ru

ОСНОВЫ ПРОГРАМИРОВАНИЯ В MATLAB 1 Операторы цикла

For count = start: step: final Команды MATLAB End Здесь count – переменная цикла; n start, final – начальное и конечное действительное значение; n step – шаг из множества действительных чисел (по умолчанию равен 1, его можно опустить). Цикл заканчивается, как становиться больше final. только count 3

Пример 1 Вычислить сумму при x= -1, 0, 1. Решение В редакторе M-file создадим файл-программу. Сохраняем её в файле Summa. m S = 0; for k = 1 : 10 S = S + x. ^ k / factorial(k); End S В командной строке x = -1: 1: 1; Summa S = -0. 6 0 1. 7 Заметим, что переменные k, s глобальные. 4

Удобнее для этого примера использовать файлфункцию. В редакторе М-файлов В командной строке создаем файл-функцию function S = funsum(x, N) > f = funsum (-1 : 1, 10) S = 0; > f = for m = 1 : N -0. 6 0 1. 7 S = S + x. ^ m / factorial(m); end Здесь переменные s, m локальные. 5

Пример 2 Создать матрицу Гильберта порядка n. Решение n = 4; a = zeros (n, n); for i = 1 : n for j = 1: n a (i, j) = 1 / (i+j-1); end a 6

Замечание Перед заполнением матриц и векторов следует сначала создать их и заполнить нулями командой zeros, для увеличения скорости алгоритма (то есть a = zeros (n, n) быстрее, чем a(i, j) = 0, i, j = 1, …, n). 7

Цикл for оказывается полезным, при выполнении повторяющихся действий, когда их число заранее известно. В случае, если их число заранее неизвестно можно воспользоваться циклом while: While условие цикла Команды MATLAB Еnd 8

Пример 3 Найти сумму ряда для заданного x До бесконечности суммировать не удастся, но можно накапливать сумму, пока слагаемые не будут слишком маленькими, например, пока 9

Замечание Малость слагаемого – понятие относительное, слагаемое, может быть, скажем, порядка 10 -10, но и сама сумма того же порядка. В этом случае нельзя останавливать суммирование. Не будем пока обращать на это внимание и вернемся к решению. 10

M-file функция В командной строке function S = mysin(x) > f = mysin (1) S = 0; 0. 8415 k = 0; while abs(x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10 S = S + (-1)^k * x. ^ (2*k + 1)/factorial(2*k + 1); k = k + 1; end 11

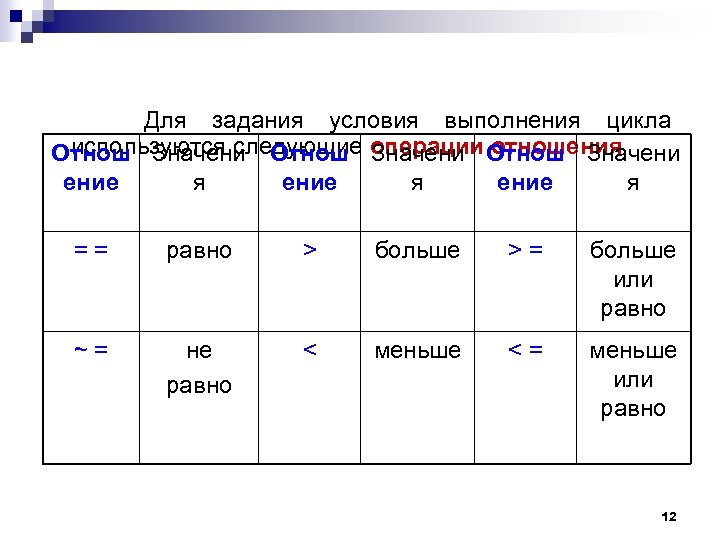
Для задания условия выполнения цикла используются следующие операции отношения Отнош Значени ение я = = равно > больше > = больше или равно ~ = не равно < меньше < = меньше или равно 12

Вернемся к нашему примеру, и заметим, что если ряд расходится, то условие на малость текущего слагаемого может никогда не выполнится и программа зациклиться. Поэтому ограничим число слагаемых 100. 000 Условие будет выглядеть так or (abs (x. ^ (2*k + 1)/factorial(2*k + 1)) > 1. 0 e -10, k

Обработка исключительных ситуаций 1) break – прерывание цикла и выполнение оператора следующего за end (например, выход из внутреннего цикла); 2) Часть некорректных математических операций в MATLAB, не приводит к завершению работы программы (например, = inf, = Na. N). Выходом является конструкция try Операторы, выполнение которых может привести к ошибке catch Операторы в случае ошибки end 15

Операторы ветвления Условный оператор В MATLAB используются следующие операторы ветвления: n if – условный оператор; n switch – оператор переключения 16

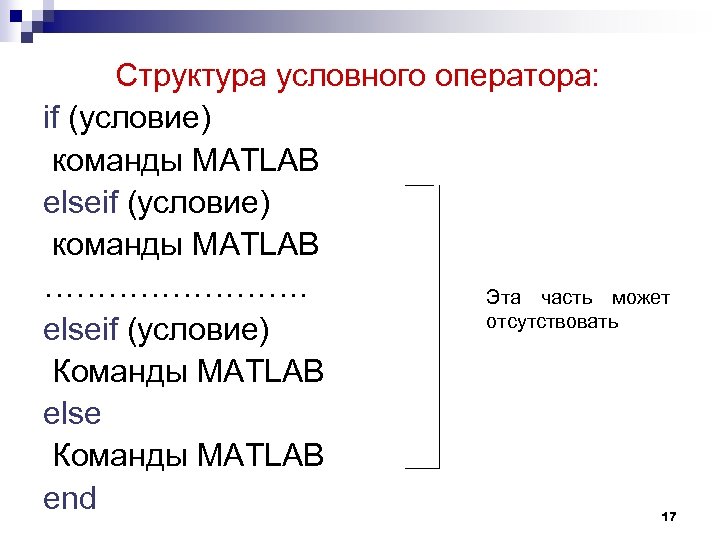
Структура условного оператора: if (условие) команды MATLAB elseif (условие) команды MATLAB …………. Эта часть может отсутствовать elseif (условие) Команды MATLAB else Команды MATLAB end 17

При составлении М-файла, использующего операторы ветвления, полезно применять 1) команду warning (‘текст’) – для вывода предупреждения в командное окно; 2) функцию error (‘текст’) – для прекращения выполнения программы. 18

Пример 4 Дано квадратное уравнение ax 2 + bx +c = 0, a ≠ 0. Напишем М-функцию вычисляющую корни квадратного уравнения. Сделаем проверку на количество входных и выходных параметров, а так же на то, что входные параметры являются числами, а не векторами и матрицами. Более того, учтем случай комплексного корня. Программа выглядит так: 19

Замечание Для написания собственных вычислительных программ большую пользу может принести самостоятельное изучение стандартных файл-функций в подкаталогах Toolbox. Большинство из них имеют открытый код, что позволяет понять принципы программирования в MATLAB. Другие функции (например, cos. m) являются встроенными. Они содержат комментарии об использовании функций. Приведем еще один пример. 21

Пример 5 Вычисление кусочно-заданной функции входным элементом, которой является матрица. Программа выглядит так: 22

function y = kusfun (x) If nargin ~= 1 error (‘Должен быть один входной аргумент’) end [Nx, Mx] = size(x); y = zeros (size(x)); % инициализирует входной аргумент for i = 1 : Nx for j = 1 : Mx if x (i, j) = -pi не нужна! y (i, j) = x (i, j) / pi; else y (i, j) = — cos(x (i, j)) end end 23

Оператор switch удобно применять тогда, когда есть соответствие между дискретными значениями некоторой переменной и последующими действиями. 24

Структура оператора видна из следующего примера: switch a case -1 disp (‘a = -1’) case 0 disp (‘a = 0’) otherwise disp (‘a не равно -1, 0’) end 25

Оператор switch хорошо подходит для решения поставленной задачи о выводе различных графиков исследуемой функции (каркасная поверхность (а=1), линии уровня (а=2) и т. д. ). 26

Логические выражения с массивами и числами Универсальным способом обработки матричных данных служат логические операции. Поскольку MATLAB представляет числа массивами 1 1, то естественно ожидать, что массивы могут входить в логические выражения. Сейчас мы рассмотрим расширение логических операций и операций отношения на случай массивов. 27

Операции отношения Результат операции отношения в MATLAB может быть или логическая единица (‘истина’) или логический нуль (‘ложь’). Причем в отличие от многих языков программирования арифметические переменные могут использоваться в одном выражении с логическими. 28

Пример 6 • > a = 1; b = 3; c = 1; > a + (b > c) ans = 2 > a + (b<=c) ans = 1 29

• > A = [1 2; 3 4]; B = [1 3; 4 5]; > C = A = = B C = 30

Замечание Так же как и в поэлементных арифметических операциях, допустимо использовать числа в качестве одного из аргументов операции отношения. В этом случае происходит сравнение каждого элемента массива с числом, результатом является массив того же размера, что и исходный. 31

Логические операции Применение логических операций к массивам приводит к поэлементному их выполнению над элементами массивов. n А and B – дает единицу, если соответствующие элементы не равны нулю; n A or B — дает единицу, если хотя бы один элемент не равен нулю; 32

not A – применяется к одному массиву, если элемент не равен нулю, то ставится нуль, иначе – единица; n all (v) – проверка наличия нулевых элементов в векторе, возвращает единицу, если нет нулевых элементов. Если v – матрица, то результат по столбцам; n any (v) – возвращает единицу, если во входном векторе есть хотя бы один ненулевой элемент. n 33

Приоритет операций 1. Отрицание; 2. Транспонирование, возведение в степень (в том числе поэлементное), знак плюс и минус перед числом; 3. Умножение и деление (в том числе поэлементное); 4. Сложение и вычитание; 5. Операции отношения; 6. Логическое ‘и’, логическое ’или’. 34

Логическое индексирование Выделение части массива, элементы которого удовлетворяют определенному условию производится функцией find. 35

Пример 7 > a = [2 3 0 -1 0 3]; > u = find ((a < 1) = -1)) 3 4 5 > anew = a(u) 0 -1 0 36

Пример 8 Заменить самостоятельно элементы квадратной матрицы 5 x 5 случайных чисел из интервала (0, 1), больших среднего значения всех элементов на 10%, на среднее значение. Решение > A = rand (5); > S = sum (sum A) / 25; > A(find (A > S* 1. 1)) = S В данном случае функция find выдает 2 вектора номера строк и номера столбцов. 37

Полиномы в MATLAB Полином p (х) =anxn+an-1 xn-1+. . . +a 0, an≠ 0 в MATLAB задается вектор-строй р=[an, an-1, . . . , a 0] , где ai – любые комплексные числа, an≠ 0. Заметим, что степень полинома вычисляется так: n=length(р)-1 (при n=0 получается const). 38

Основные команд для действий с полиномами таковы: n n n r=roots(р) – вектор-столбец, содержащий все корни полинома; p=poly(r) – построение полинома по корням, заданным в векторе-столбце r, причем, если r квадратная матрица, то р — характеристический многочлен; y=polyval(p, x) – поэлементное вычисление у значений полиному р на множестве х, где х может быть вектором или матрицей; 39

n n n polyder(p) – вектор-строка, производная от p (дифференцирование полинома p); polyder(p, q) –производная от произведения полиномов p и q; [a, b]= polyder(p, q) – производная от частного полиномом p и q, где a и b являются числителем и знаменателем получившейся дроби; 40

n n n p=polyfit(x, y, n) – приближение функции y(x) полиномом p n-й степени по методу, минимизирующему расстояние между графиком полинома и истиной кривой, усредненное по всей их длине; conv(p, q) – вектор-строка, произведение полиномов p и q; [w, r]=deconv(p, q) – деление p на q, причем w-частное, r-остаток и p=conv (q, w) +r; 41

n [r, p, k]=residue(a, b) – разложение рациональной функции на простые дроби над полем комплексных чисел с выделением целой части k(х) или где ri – вычеты (элементы r), pi – полюса (элементы p). Эта команда работает и в обратную строну [a, b] =residue(r, p, k) 42

Замечание 1. Если в residue (a, b) полином b(х), а в roots(p) полином р(х) имеют кратные или близкие друг к другу корни, то результаты могут быть неверными, поскольку такая задача плохо обусловлена. Плохая обусловленность – это крайне сильная зависимость результата от коэффициентов (аналог устойчивости решения в дифференциальных уравнениях). 43

2. При работе с полиномами возникают полиномы вида [0, . . . ], а MATLAB автоматически не проверяет an≠ 0, и возникают ошибки (нужно самим следить). 44

Источник: present5.com