Лекция 3 повышают производительность работы. Эффективное решение состоит в оформлении собственных алгоритмов в виде программ (М-файлов), которые можно запустить из рабочей среды или из редактора. Встроенный в MATLAB редактор М-файлов позволяет не только набирать текст программы и запускать ее целиком или частями, но и отлаживать алгоритм.
Подробная классификация М-файлов приведена ниже. 1.1. Работа в редакторе М-файлов. Для подготовки, редактирования и отладки m-файлов служит специальный многооконный редактор. Он выполнен как типичное приложение Windows.
Редактор можно вызвать командой edit из командной строки или командой главного меню File | New | M-file . После этого в окне редактора можно создавать свой файл, пользоваться средствами его отладки и запуска. Перед запуском файла его необходимо записать на диск, используя команду File | Save as в меню редактора. На рис.1 показано окно редактора/отладчика.
Подготовленный текст файла (это простейшая и наша первая программа на языке программирования MATLAB) можно записать на диск. Для этого используется команда Save As , которая использует стандартное окно Windows для записи файла с заданным именем. Следует отметить, что имя М-файла должно быть уникально, а требование к имени файла такое же, как для имен переменных среды MATLAB.
MATLAB 03 Написание программ
После записи файла на диск можно запустить команду Run на панели инструментов или меню Debug , или просто нажать ., для того чтобы исполнить m-файл. На первый взгляд может показаться, что редактор/отладчик — просто лишнее звено в цепочке «пользователь — MATLAB». И в самом деле, текст файла можно было бы ввести в окно системы и получить тот же результат.
Однако на деле редактор/отладчик выполняет важную роль. Он позволяет создать m-файл (программу) без той многочисленной «шелухи», которая сопровождает работу в командном режиме. Текст такого файла подвергается тщательной синтаксической проверке, в ходе которой выявляются и отсеиваются многие ошибки пользователя.
Таким образом, редактор обеспечивает синтаксический контроль файла. Редактор имеет и другие важные отладочные средства — он позволяет устанавливать в тексте файла специальные метки, именуемые точками прерывания ( breakpoints ). При их достижении вычисления приостанавливаются, и пользователь может оценить промежуточные результаты вычислений (например, значения переменных), проверить правильность выполнения циклов и т. д. Наконец, редактор позволяет записать файл в текстовом формате и увековечить ваши труды в файловой системе MATLAB.
Для удобства работы с редактором/отладчиком строки программы в нем нумеруются в последовательном порядке. Редактор является многооконным. Окно каждой программы оформляется как вкладка. Редактор-отладчик позволяет легко просматривать значения переменных.
Для этого достаточно подвести к имени переменной курсор мыши и задержать его — появится всплывающая подсказка с именем переменной и ее значением. Очень удобной возможностью редактора М-файлов является выполнение части команд. Для этого используется команда Evaluate Selection из контекстного меню или главного меню Text , или просто функциональная клавиша , которые позволяют выполнить выделенный текст программы.
MATLAB 01 Начало работы
Лекция 3 Рис. 1. Окно редактора М-файлов. 1.2. Типы М-файлов. Файл-программы. М-файлы в MATLAB бывают двух типов: файл-программы (Script M-Files) , содержащие последовательность команд, и файл-функции (Function M-Files) , в которых описываются функции, определяемые пользователем.
Файл-программы представляют собой простейший тип М-файлов. Они не имеют входных и выходных аргументов и оперируют переменными, существующими в рабочей среде, или могут создавать новые переменные. Файл-программу mydemo вы написали при прочтении предыдущего раздела. Все переменные, объявленные в файл-программе, становятся доступными в рабочей среде после ее выполнения.
Запустите файл-программу mydemo , приведенную в листинге рис.1. Перейдите в окно Workspace и убедитесь, что все введенные в М-файле переменные появились в рабочей среде. Все созданные при исполнении М-файла переменные остаются в рабочей среде после его завершения, и их можно использовать в других файл-программах и в командах, выполняемых из командной строки.
Запуск файл-программы осуществляется двумя способами. 1. Из редактора М-файлов так, как описано выше. 2. Из командной строки или другой файл-программы, при этом в качестве команды используется имя М-файла (без расширения). Применение второго способа намного удобнее, особенно если созданная файл-программа будет неоднократно использоваться впоследствии.
Фактически созданный М-файл становится командой, которую понимает MATLAB. Закройте все графические окна и наберите в командной строке mydemo , появляется графическое окно, соответствующее командам файл-программы mydemo.m . После ввода команды mydemo MATLAB производит следующие действия.
Лекция 3 1. Проверяет, является ли введенная команда именем какой-либо из переменных, определенных в рабочей среде. Если введена переменная, то выводится ее значение. 2. Если введена не переменная, то MATLAB ищет введенную команду среди встроенных функций. Если команда оказывается встроенной функцией, то происходит ее выполнение.
3. Если введена не переменная и не встроенная функция, то MATLAB начинает поиск М-файла с названием команды и расширением m. Поиск начинается с текущего каталога (Current Directory); если М-файл в нем не найден, то MATLAB просматривает каталоги, установленные в пути поиска (Path). (Для установки текущего каталога можно использовать окно выбора с одноименным названием на панели инструментов или команду cd . Установка путей поиска осуществляется с помощью команды Set Path команды меню File или с помощью команды addpath ). Если ни одно из вышеперечисленных действий не привело к успеху, то в командное окно выводится сообщение, например, если сделать ошибку. Последовательность поиска MATLAB говорит о том, что очень важно правильно задавать имя собственной файл-программы при сохранении ее в М-файле.
Во-первых, ее имя не должно совпадать с именем существующих функций в MATLAB. Узнать, занято имя или нет можно при помощи функции exist . Во-вторых, имя файла не должно начинаться с цифры, знаков «+» или «-«, словом с тех символов, которые могут быть интерпретированы MATLAB как ошибка при вводе выражения.
Например, если вы назовете М-файл с файл-программой 5prog.m, то при ее запуске из меню редактора или по получите сообщение об ошибке. Это не удивительно, т. к. MATLAB ждет от вас 5 + prog (или 5, prog) для вычисления арифметического выражения с переменной prog (или добавления 5 в качестве первого элемента к вектор-строке prog).
Следовательно, правильным было бы имя prog5.m (или хотя бы p5rog.m), но только начинающееся с буквы. Обратите внимание, что если вы запускаете на выполнение выделенные команды (могут быть выделены все команды) М-файла с неверным именем при помощи , то ошибки не будет.
Фактически происходит последовательное выполнение команд, не отличающееся от их вызова из командной строки, а не работа файл-программы. Очень распространена еще одна ошибка при задании имени файл-программы, которая на первый взгляд имеет необъяснимые последствия: программа запускается только один раз. Повторный запуск не приводит к выполнению программы.
Разберем эту ситуацию на примере файл-программы из листинга 5.1, которую вы сохранили в файле mydemo.m. Переименуйте файл в x.m, затем удалите все переменные рабочей среды из окна браузера переменных Workspace или из командной строки: >> clear all Выполните файл-программу, например, из редактора, нажав . Появляется графическое окно с двумя графиками и ничего не предвещает подвоха.
Закройте теперь графическое окно и запустите программу снова. Графическое окно больше не создается, зато в командное окно вывелись значения массива x в соответствии с первым пунктом приведенного выше алгоритма поиска MATLAB. Эти обстоятельства следует учитывать при выборе имени файл-программы.
Не менее важный вопрос связан с третьим пунктом алгоритма поиска MATLAB – текущим каталогом и путями поиска. Как правило, собственные М-файлы хранятся в каталогах пользователя. Для того чтобы система MATLAB могла найти их, следует установить пути, указывающие расположение М-файлов. 1.3. Файл-функции.
Рассмотренные выше файл-программы являются последовательностью команд MATLAB, они не имеют входных и выходных аргументов. Для решения вычислительных задач и написания собственных приложений в MATLAB часто требуется программировать файл-функции, которые производят необходимые действия с входными аргументами и возвращают результат в выходных аргументах. Число входных и выходных аргументов зависит от решаемой задачи – может быть только один входной и один выходной аргумент, несколько и тех и других, или только входные аргументы.
Лекция 3 Возможна ситуация, когда входные и выходные аргументы отсутствуют. В этом разделе разобрано несколько простых примеров, позволяющих понять работу с файл-функциями. Файл-функции, так же как и файл-программы, создаются в редакторе М-файлов. Файл-функции с одним входным аргументом. Предположим, что в вычислениях часто необходимо использовать значение функции:
| e | − x x 2 | + 1 | |
| x 4 | + 0.1 | ||
Имеет смысл один раз написать файл-функцию, а потом вызывать ее всюду, где необходимо вычисление этой функции для заданного аргумента. Для этого необходимо открыть в редакторе М- файлов новый файл и набрать текст: function f = myfun(x) f = exp(-x)*sqrt((x^2 + 1)/(x^4 + 0.1)); Слово function в первой строке определяет, что данный файл содержит файл-функцию.
Первая строка является заголовком функции, в которой размещаются имя функции и списки входных и выходных аргументов. Входные аргументы записываются в круглых скобках после имени функции. В нашем примере есть только один входной аргумент – х. Выходной аргумент f указывается слева от знака равенства в заголовке функции.
При выборе имени файл-функции следует позаботиться об отсутствии конфликтов с занятыми именами в MATLAB. Аналогичный вопрос мы обсуждали выше: как сохранить файл-программу в файле с уникальным именем. Тот же самый подход, основанный на обращении к функции exist , вы можете применить для задания имени файл-функции.
После заголовка размещается тело файл-функции – один или несколько операторов (их может быть достаточно много), которые реализуют алгоритм получения значения выходных переменных из входных. В нашем примере алгоритм простой – по заданному х вычисляется арифметическое выражение и результат записывается в f. Теперь необходимо сохранить файл в рабочем каталоге или в другом, известном для MATLAB, месте.
При выборе пунктов Save или Save as. меню File по-умолчанию предлагается имя файла, совпадающее с названием функции myfun. Необходимо сохранить файл-функцию с этим предложенным именем.
Теперь созданную функцию можно использовать так же, как и встроенные sin, cos и другие, например, из командной строки: >> y=myfun(1.3) y = 0.2600 При создании файл-функции myfun мы подавили вывод значения f в командное окно, завершив оператор присваивания точкой с запятой. Если этого не сделать, то оно выведется при обращении y=myfun(1.3) . Как правило, лучше избегать вывода в командное окно результатов промежуточных вычислений внутри файл-функции. Файл-функция, приведенная в предыдущем примере, имеет один существенный недостаток. Попытка вычисления значений функции от массива приводит к ошибке, а не к массиву значений так, как это происходит при использовании встроенных функций. >> x=[1.3 7.2]; >> y=myfun(x) . Error using ==> ^ Matrix must be square. Error in ==> C:MATLAB6p5workmyfun.m On line 2 ==> f = exp(-x)*sqrt((x^2 + 1)/(x^4 + 0.1));
Лекция 3 Кроме функций с несколькими аргументами, MATLAB позволяет создавать функции, возвращающие несколько значений, т. е. имеющих несколько выходных аргументов. Файл-функции с несколькими выходными аргументами. Файл-функции с несколькими выходными аргументами удобны при вычислении функций, возвращающих несколько значений (в математике они называются вектор-функции).
Выходные аргументы добавляются через запятую в список выходных аргументов, а сам список заключается в квадратные скобки. Следующий пример приводит файл-функцию hms для перевода времени, заданного в секундах, в часы, минуты и секунды: function [hour, minute, second] = hms(sec) hour = floor(sec/3600); minute = floor((sec — hour*3600)/60); second = sec — hour*3600 — minute*60; При вызове файл-функций с несколькими выходными аргументами результат следует записывать в вектор соответствующей длины: >> [H, M, S] = hms(10000) H = 2 M = 46 S = 40 Если при использовании данной функции явно не указывать выходные параметры, то результатом вызова функции будет только первый выходной аргумент: >> hms(10000) ans = 2 Если список выходных аргументов пуст, т. е. заголовок выглядит так: function myfun(a, b) или function [ ] = myfun(a, b) , то файл-функция не будет возвращать никаких значений. Такие функции тоже иногда оказываются полезными. Функции MATLAB обладают еще одним полезным качеством — возможностью получения информации о них при помощи команды help , например, help fplot . Собственные файлфункции так же можно наделить этим свойством, используя строки комментариев. Все строки комментариев после заголовка и до тела функции или пустой строки выводятся в командное окно командой help . Например для нашей функции можно создать подсказку: function [hour, minute, second] = hms(sec) %hms — перевод секунд в часы, минуты и секунды % Функция hms предназначена для перевода секунд % в часы минуты и секунды. % [hour, minute, second] = hms(sec) hour = floor(sec/3600); minute = floor((sec — hour*3600)/60); second = sec — hour*3600 — minute*60;
Лекция 3 Здесь count — переменная цикла, start – ее начальное значение, final – конечное значение, a step – шаг, на который увеличивается count при каждом следующем заходе в цикл. Цикл заканчивается, как только значение count становится больше final . Переменная цикла может принимать не только целые, но и вещественные значения любого знака.
Приведем пример применения цикла for . Пусть требуется вывести графики семейства кривых для x [0, 2 π ], которое задано функцией y ( x , a ) = e − ax sin x , зависящей от параметра a , для значений параметра а от -0.1 до 0.1 с шагом 0.02. Можно, конечно, последовательно вычислять у(х, а) и строить ее графики для различных значений а , но гораздо удобнее использовать цикл for . Текст файл-программы: figure % создание графического окна x = 0:pi/30:2*pi; % вычисление вектора значений аргумента % перебор значений параметра в цикле for a = -0.1:0.02:0.1 % вычисление вектора значений функции для текущего значения . параметра y = exp(-a*x).*sin(x); % добавление графика функции hold on plot(x, y) end В результате выполнения этой файл-программы появится графическое окно, изображенное на рис.
2, которое содержит требуемое семейство кривых. Рис. 2. Семейство кривых. Циклы for могут быть вложены друг в друга, при этом переменные вложенных циклов должны быть разными. Вложенные циклы удобны для заполнения матриц. Пример создания матрицы Гильберта: n = 4; a = zeros(n); for i = 1:n for j = 1:n a(i, j) = 1/(i+j-1); end end
Лекция 3 В заключение этого раздела отметим еще одну особенность цикла for , которая наряду с возможностью задания вещественного счетчика цикла с постоянным шагом делает цикл for достаточно универсальным. В качестве значений переменной цикла допускается использование массива значений: for count = A команды MATLAB end Если А — вектор-строка, то count последовательно принимает значение ее элементов при каждом заходе в цикл. В случае двумерного массива А на i -ом шаге цикла count содержит столбец А(:,i) . Разумеется, если А является вектор-столбцом, то цикл выполнится всего один раз со значением count , равным А . Цикл for оказывается полезным при выполнении определенного конечного числа действий. Существуют алгоритмы с заранее неизвестным количеством повторений, реализовать которые позволяет более гибкий цикл while . Цикл while . Цикл while служит для организации повторений однотипных действий в случае, когда число повторений заранее неизвестно и определяется выполнением некоторого условия. Рассмотрим пример разложение sin(x) в ряд:
| ∞ | k | x 2 k + 1 |
| S ( x ) = ∑ ( − 1 ) | ||
| ( 2 k + 1 ) ! | ||
| k = 0 | ||
Конечно, до бесконечности суммировать не удастся, но можно накапливать сумму с заданной точностью, например, 10 -10 . Очевидно, что число членов ряда в данном случае неизвестно, поэтом использование оператора for невозможно. Выход состоит в применении цикла while , который работает, пока выполняется условие цикла: while условие повторения цикла команды MATLAB end В данном примере условием повторения цикла является то, что модуль текущего слагаемого x 2 k + 1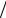 
( 2 k + 1 ) ! больше 10 -10 . Текст файл-функции mysin, вычисляющей сумму ряда на основе рекуррентного соотношения:
| a | k | = | x 2 | a | k − 1 |
| 2 k (2 k + 1) |
function s = mysin(x) % Вычисление синуса разложением в ряд % Использование: у = mysin(x), -pi < х < pi % вычисление первого слагаемого суммы для к = О k = 0; u = x; s = u; % вычисление вспомогательной переменной x2 = x*x; while abs(u) >1.0e-10 k = k + 1; u = -u* x2/(2*k)/(2*k + 1); s = s + u; end
Источник: studfile.net
Основы Matlab
Здравствуйте, уважаемые читатели! В нашей статье, посвященной основам программирования MatLab, мы познакомимся с синтаксисом этого языка, который мы будем использовать в основном для математических вычислений. MATLAB — это интерактивная система, в которой основным элементом данных является массив. Это позволяет решать различные задания, связанные с техническими вычислениями, особенно в которых используются вектора и матрицы, в несколько раз быстрее, чем при написании программ с использованием других языков программирования.
Переменные в MATLAB:
- logical (true – 1, false – 0)
- char – символьная строка
- numeric – массивы чисел с плавающей запятой
- int: int8 (массив 8-разрядных целых чисел со знаком, 1 байт на одно число), также есть int16, int32, int64
- single – массив чисел с плавающей запятой одинарной точности (4 байта на одно число)
- double – массив чисел с плавающей запятой двойной точности (16 знаков)
- structure – структурированный массив полей для хранения данных с именами
Имя переменной:
длина — до 63 символов;
не должно совпадать с именами функций и процедур;
должно начинаться с буквы;
может содержать буквы, цифры, знак подчёркивания;
различаются большие и маленькие буквы.
Задать переменную очень легко:
>> a=2;b=4;a+b ans = 6
Как видите, Matlab сам выводит результат операции с 2 переменными.
Массивы:
Начнем с задания одномерных массивов:
Задание в командной строке: x = [1,2,3,4] или x = [1 2 3 4]
Задание отдельных элементов: х(3) = 3
Длину массива можно найти командой: length (x)
Переходим к двумерным массивам:
Задание в командной строке: x = [1,2,3,4;5,6,7,8]
ans = 1 2 3 4 5 6 7 8
Задание отдельных элементов: х(2,3) = 7
Обращение к отдельной р-ой строке массива: у = [р,:]
Обращение к к-ому столбцу массива: у = [:,к]
Команда В=А(. ) обращается ко всем элементам матрицы, т.е. создаёт копию матрицы А.
Также следует знать о стандартных матрицах:
- zeros(n,m) — матрица из нулей размера nxm
- ones(n,m) – матрица из единиц размера nxm
- rand(n,m) – матрица случайных чисел размера nxm
- eye(n,m) – матрица из единиц на главной диагонали размера nxm
Операторы:
Операторы следует знать, так как без них невозможно освоить все основы программирования на MATLAB.
- Арифметические операторы (арифметические выражения, вычисления)
- Операторы отношения (сравнение аргументов)
- Логические операторы (логические выражения)
Уровни приоритета арифметических операторов:
- Поэлементное транспонирование (.’ ), поэлементное возведение в степень (.*), сопряжение матрицы (‘), возведение матрицы в степень(^)
- Унарный плюс(+) и унарный минус (-)
- Поэлементное умножение массивов(.*), правое деление массивов (./) и левое (.), умножение матриц (*), решение систем линейных уравнений операции (/) и ()
- Сложение (+) и вычитание массивов (-)
- Оператор (:)
Внутри каждого уровня операторы имеют равный приоритет и вычисляются в порядке следования слева направо. Порядок вычислений может быть изменён скобками.
- меньше — функция lt()
- меньше или равно — функция le()
- > — больше — функция gt()
- >= — больше или равно — функция ge()
- == — равно — функция eg()
- ~= — не равно — функция ne()
Их приоритет ниже арифметических, но выше логических операторов.
- функция and()
- | — массив: 1- для каждого местоположения, в котором хотя бы один элемент имеет значение true (отличен от нуля) и 0 – для всех остальных элементов; функция or()
- ~ — логическое отрицание для каждого элемента входного массива, А; функция not()
- xor — массив: 1- для каждого местоположения, в котором только один элемент имеет значение true (отличен от нуля) и 0 – для всех остальных элементов
A = [0 1 1 0 1]; B = [1 1 0 0 1]; A> rand(3,4) ans = 0.8147 0.9134 0.2785 0.9649 0.9058 0.6324 0.5469 0.1576 0.1270 0.0975 0.9575 0.9706
Далее определим детерминант следующей матрицы:
>> x = [1,2,3,4;5,6,7,8;10,11,12,13;14,15,16,17] x = 1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17
>> det(x) ans = 0
Идем дальше:
Приведем пример перемножения матриц, напомню, что матрицы можно перемножать только в том случае, если число столбцов 1 матрицы совпадает с числом строк 2 матрицы.
>> x = [1,2,4;5,6,7] X1 = 1 2 4 5 6 7 >> x = [1,2;4,5;6,7] X2 = 1 2 4 5 6 7 >> x1*x2 ans = 11 14 18 29 38 51 41 54 73
На этом мы сегодня закончим. В следующих статьях мы будем уже подробно разбираться со всеми возможностями MATLAB. И поверьте, возможности эти очень большие.
Если у вас остались вопросы, то задавайте их в комментариях.
Поделиться ссылкой:
Источник: codetown.ru
Работа с окном команд и редактором в MATLAB
2 Работа с редактором в среде MATLAB
Чтобы упростить жизнь учёному, инженеру или студенту, служит окно редактора (Editor). Давайте откроем окно редактора через меню Desktop Editor.
В окне редактора можно создавать новые переменные, строить графики, писать программы (скрипты), создавать компоненты для обмена с другими средами, создавать приложения с пользовательским интерфейсом (GUI), а также редактировать имеющиеся.
Нас в данный момент интересует написание программы, содержащей функции для повторного использования в будущем. Поэтому идём в меню File редактора и выбираем New M-File.
М-файлами в среде МАТЛАБ называются файлы, содержащие текст программ (скрипты) или определённые пользователем функции.
Давайте напишем в редакторе простую функцию draw_plot:
function draw_plot(x) % Задаём первую функцию: y = log(x); % Строим первый график: subplot(1, 2, 1), plot(x, y); % Задаём вторую функцию: y = sqrt(x); % Строим второй график: subplot(1, 2, 2), plot(x, y);
