Классическое программированное обучение, образованное концепциями Скиннера и Кроудера, может использоваться в образовании исключительно как дополнительный метод, один из многих, но не единственный. Им можно пользоваться при закреплении знаний, а также при контроле и оценке степени овладения ими.
Спирина Анжелика Владимировна
Содержимое разработки
Автономная некоммерческая организация дополнительного профессионального образования
«Уральский институт повышения квалификации и переподготовки»
Программа профессиональной переподготовки:
«Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Дисциплина: математика
Практическое задание 1, модуль 1
слушатель Спирина А. В.
Преподаватель:
к.п.н. Гладнева С. Г.
Уральский Институт Повышения Квалификации и Переподготовки – 2017
Практическое задание 1
- Требования Федерального государственного образовательного стандарта основного общего образования и Федерального государственного образовательного стандарта среднего (полного) общего образования к содержанию математического образования.
- Научные и методические основы школьного курса математики, принципы построения программ по математике для основного и среднего (полного) образования и реализующих программы учебников.
- Задачи и пути развития математической речи учащихся основной и средней (полной) школы.
- Разбираться в содержании и требованиях программ по математике, в содержании и методическом аппарате школьных учебников, в структуре и замысле пособий для учащихся, реализовывать требования программ, методические возможности учебников и учебных пособий.
- Самостоятельно планировать изучение разделов и тем школьного курса математики, циклы уроков и отдельные уроки, в том числе с использованием инновационных технологий.
- Изучать уровень математических знаний и умений школьников, оценивать результаты математического образования.
- Устанавливать межпредметные связи между методикой преподавания математики, педагогикой, психологией, математикой.
- Изучать передовой опыт учителей, элементарно оценивать его.
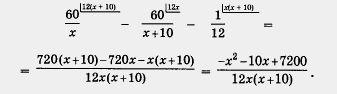
Учебники в Американской школе (Математика)
Преобразуем левую часть уравнения
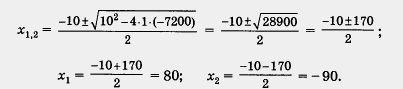
Приравняв числитель этой дроби нулю, получим квадратное уравнение — х 2 — 10х + 7200 = 0 или, переходя к более удобной записи, х 2 + 10х — 7200 = 0.
Применяя известную формулу, находим

-82%
Источник: videouroki.net
§ 3. Содержание школьного курса математики
Школьным учебным планом на изучение математики с I по X класс отводится около 2000 учебных часов 1 . Кроме того, дополнительные часы на изучение математики предусматриваются в системе факультативных курсов (VII—X классы) 2 .
Виленкин. 5 класс за час. Математика в средней школе
Учебная программа советской школы основывается на принципах соответствия программы основным целям школы, обеспечивает преемственность получаемой учащимися подготовки в I—III классах (начальная школа), IV—VIII классах (восьмилетняя школа), IX—X классах (средняя школа).
Учащиеся, которые после окончания восьмилетней школы будут завершать среднее образование в системе профессионально-технических училищ, в средних специальных учебных заведениях, в вечерних (заочных) школах, должны получить математическую подготовку в том же объеме, что и учащиеся, оканчивающие среднюю общеобразовательную школу. Таким образом, все учащиеся, получившие среднее образование, приобретают равную возможность для продолжения образования.
«Ядро» современной программы по математике составляют:
1. Числовые системы.
3. Уравнения и неравенства.
4. Тождественные преобразования математических выражений.
7. Геометрические фигуры и их свойства. Измерение геометрических величин. Геометрические преобразования.
9. Начала математического анализа.
10. Основы информатики и вычислительной техники.
Каждый из вошедших в это «ядро» разделов имеет свою историю развития как предмет изучения в средней школе. На каком возрастном этапе, в каких классах, с какой глубиной и при каком числе часов изучаются эти разделы, определяет программа по математике для средней школы 3 . Вопросы их изучения будут подробно рассматриваться в специальной методике преподавания математики. Сейчас ограничимся отдельными краткими пояснениями.
Раздел «Числовые системы» изучается на протяжении всех лет обучения. В школьную программу вопросы числовых систем входили уже в далеком прошлом. Но с течением времени происходило значительное снижение возраста, в котором учащиеся изучали включаемые в программу темы, возрастала глубина их изложения. В настоящее время изыскиваются возможности включения в программу заключительной темы этого раздела — «Комплексные числа».
Изучение величин в программах и учебниках по математике не выделено в специальный раздел. Но на протяжении всех лет обучения учащиеся выполняют действия с различными величинами при решении задач, особенно задач, отражающих связи курса математики с дисциплинами естественнонаучного, технического циклов.
Изучению уравнений и неравенств посвящается значительная часть всего учебного времени. Особая значимость этой темы состоит в широком применении уравнений и неравенств в самых различных областях приложений математики. До недавнего времени систематическое изучение уравнений начиналось лишь с VI класса. В течение последних десятилетий знакомство с уравнениями и применение уравнений к решению задач вошло в курс математики начальной школы и IV—V классов.
Координаты и функции вошли в курс математики средней школы только в первой четверти XX в. Характерной особенностью современного школьного курса математики являются расширение этих разделов и возрастающая роль метода координат и функций в изучении других тем школьной программы.
Наибольшую остроту в обсуждении вопросов его содержания приобрел в последние десятилетия курс геометрии. Здесь в значительно больших размерах, чем в других разделах школьного курса математики, возникли проблемы соотношения традиционного содержания с необходимыми новыми дополнениями. Однако при всех различиях в подходах к решению этой проблемы получило общее одобрение включение в курс геометрических преобразований.
Векторы впервые вошли в курс геометрии нашей школы только в середине 70-х годов. Большая общеобразовательная значимость этой темы, обширные практические применения обеспечили ей общее признание. Однако вопросы доходчивого для всех учащихся изложения этого раздела в школьных учебниках, применения векторов к решению содержательных задач находятся еще в стадии разработки и могут найти свое решение только на основе глубокого анализа и учета результатов школьного преподавания.
Элементы математического анализа вошли в программу советской общеобразовательной школы недавно. Включение в программу этих разделов вызвано их большой идейной и прикладной значимостью.
Последний из разделов — основы информатики и вычислительной техники — отражает требования, предъявляемые к современной математической подготовке молодежи в связи с широким внедрением в практику электронно-вычислительных машин.
Как отмечалось ранее, новые научные достижения, их развитие и внедрение в практику приводят к пересмотру школьного курса математики. Происходит идейное и прикладное обогащение курса. Кроме того, из содержания школьного образования исключаются менее важные разделы и на смену им приходят новые вопросы, приобретающие более высокую как теоретическую, так и практическую ценность.
С развитием математики и ее приложений возрастает число разделов, обоснованно ждущих своего включения в школьный курс математики. Но возможности общего среднего образования небеспредельны, они ограничены как сроком обучения, так и пределами разумной учебной нагрузки учащихся.
Несмотря на то что уже сейчас стало ясным, что для всеобщего среднего образования важно иметь в курсе средней школы элементы теории вероятности, статистики, что важно строить школьный курс так, чтобы учащиеся были подготовлены к восприятию новых аспектов прикладной математики, эти назревшие вопросы оказались весьма сложными для их практической реализации. Возможные формы включения ряда новых разделов в обязательный курс математики средней школы пока не найдены. В связи с этим обсуждается вопрос о том, что именно из прикладных вопросов должно войти в школьное обучение в ближайшем будущем. В то же время высказывается и такое мнение, что в программу не надо вводить специальных разделов прикладной математики, а идти по пути включения в курс таких тщательно отобранных задач, решение которых приводит к рассмотрению ситуаций, которые нужно математизировать, чтобы прийти затем к математическим моделям. Таким образом, предполагается установить более тесную взаимосвязь теоретического содержания математического образования с практикой применения учащимися приобретаемых математических знаний.
Как показывает история развития школьного математического образования, это становится выполнимым в результате:
1) происходящего в изучаемом предмете процесса обобщения (генерализации) входящих в него понятий, рассматриваемых фактов;
2) все возрастающего применения математических знаний и их приложений в повседневной практике, что приводит к предварительному ознакомлению детей в их жизненном опыте с понятиями, подлежащими изучению;
3) совершенствования методов и средств обучения.
Включение в школьный курс основных разделов становится возможным, если каждый из перечисленных факторов учтен в должной для этого мере.
Выделенное ядро школьного курса математики составляет основу его базисной программы, в которой материал расположен не по классам, а по ступеням обучения (I—III, IV—V, VI—VIII, IX—X классы) и излагается согласно логике развития ведущих научно-методических линий.
Базисная программа обязательна для всех учебных заведений, дающих среднее образование, она является для них исходным документом для разработки тематических программ. В тематической программе для средней школы, кроме распределения учебного материала по классам, излагаются требования к знаниям, умениям и навыкам учащихся, раскрываются межпредметные связи, примерные нормы оценок. В программе подробно освещаются вопросы формирования научного мировоззрения, воспитания учащихся в процессе обучения.
В содержании математического образования, в результатах, которые должны быть получены в процессе обучения, можно выделить следующие аспекты:
I1. Совокупность необходимой для усвоения и запоминания информации.
I2. Система выводимых одно из другого понятий.
II1. Совокупность приобретаемых оперативных навыков.
II2 . Система взаимосвязанных способностей.
В последние десятилетия предметом острых дискуссий стали вопросы о том, какова в современных условиях значимость каждого из этих аспектов. Не происходит ли постепенная утрата значимости аспектов I1 и II1 при возрастающей значимости для результатов процесса обучения аспектов I2 и II2?
Но становится все более очевидной необходимость одинаково большого внимания к каждому из этих аспектов, причем каждый из них получает свое развитие, приобретает новые особенности.
Нарушение этого требования влечет за собой отрицательные последствия, и прежде всего возникновение формализма в математической подготовке учащихся: приобретаемые учащимися знания не становятся опорой для осознанного приобретения необходимых практических навыков; получаемые практические навыки, не подкрепленные знаниями, быстро утрачиваются или применяются там, где это применение не является необходимым и даже не имеет смысла.
Источник: studfile.net
Документы ФГОС учителю математики
“Примерная основная образовательная программа основного общего образования” одобрена решением федерального учебно-методического объединения по общему образованию (протокол от 8 апреля 2015 г. № 1/15)
Предметное результаты ООО. Математика
Приказ Минобрнауки РФ от 17.05.2012 №413 ( в ред. от 31.12.2015) “Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования”
Требования к результатам освоения ООП СОО
Предметные результаты освоения ООП СОО
“Примерная основная образовательная программа среднего общего образования” одобрена решением федерального учебно-методического объединения по общему образованию (протокол от 28 июня 2016 г. № 2/16-з)
Планируемые предметные результаты освоения ООП СОО
Математика: алгебра и начала математического анализа, геометрия
Источник: aujc.ru