В настоящее время в н.кл. реализуются следующие программы обучения математике:
- Система «Школа России» — программа по математике разработана Моро М.И. и др. (традиционная программа)
- Система Занкова Л.В. – программа разработана Аргинской И.И
- Система «Школа 2100» — программа по математике: а) разработана Петерсон Л.Г. б) разработана Демидовой Т.Е., Козловой С.А., Тонких А. П. «Моя математика»
- Система «Школа 21 века» — программа по математике Рудницкая В.Н.
- Система «Гармония» программа Истоминой Н.Б.
- Система Д.Б. Эльконина-Довыдова В.В. — программа по математике а) Александрова Э.И., б) Давыдов В.В.
Дополнительно, вне системы, разработаны другие программы по математике. Например, Эрдниев П.М.
1. Учебник по математике Александровой э.И. Общеобразовательной школы
(1-4), работающая по программе развивающего обучения (система Д.Эльконина- В.Давыдова)на основе концепции развития личности ребёнка в школе.
лучший учебник по математике (начальная школа), ошибки начальной школы в математике — Л. А. Ясюкова
1.Цель системы: развитие теоретич. мышления (анализ, синтез, планирование) в условиях формирования учебной деятельности.
2.Задачи курса математики: 1. формировать теоретическое сознание
2. передать детям не столько ЗУНы, сколько способы умственных действий
3. воспроизвести в учебной деятельности детей логику научного познания
Характерной особенностью данного курса математики в отличие от аналогичных курсов развивающего образования (по системе Д.Б. Эльконина-В.В. Давыдова) является его направленность на воспитание, развитие личности ребенка на основе вышеописанных идей, где формирование предпосылок теоретического мышления составляет лишь средство для достижения образовательной цели, причем образцы воспитания не задаются извне, а реализуются через формы сотрудничества в ходе усвоения математики. Это обеспечивает не только самоизменение конкретной личности, но и класса в целом, который выступает в качестве основной референтной группы в системе жизнедеятельности ребенка.
«Обеспечение условий для становления ребенка как субъекта учебной деятельности (а не объекта педагогических воздействий), заинтересованного в самоизменении и способного к нему, — вот задача развивающего образования на основе содержательного обобщения учебного материала» (В.В Давыдов).
Особенности курса математики по данной программе:
Все отличия данного варианта реализации концепции развивающего образования сводятся к трем основным характеристикам, связанным с развертыванием математического содержания, с методическими подходами и с учетом жизненного опыта ребенка и меняющимися социальными условиями.
Рассмотрим их в указанной последовательности.
I. Логика построения курса и его наполнение во многом отличается от предлагаемых другими авторами.
— В первом классе дети учатся сравнивать предметы не только по цвету, материалу, форме, количеству, длине, площади, объему, массе, а и по расположению в пространстве, по назначению, по «красоте» и еще ряду признаков, из которых впоследствии выделяются величины — не только длина, площадь, объем, масса и количество, но и угол.
— Буквы латинского алфавита (в отличие от других авторов, которые используют только русский алфавит) вводятся в самом начале обучения, что позволяет использовать естественный знаковый математический язык. Вводятся и новые значки, которых не существует в математической культуре, но которые помогают ребенку более глубоко осознать смысл рассматриваемого понятия, в частности, понятия части и целого. Например:
-Всякий новый знак, схема, равно как и новое понятие, появляется лишь тогда, когда возникает осознанная потребность именно в этом значке, схеме, понятии и выглядит как придуманное самим ребенком.
-Перед введением понятия числа (целого неотрицательного) включена новая тема «Какие бывают мерки?», позволяющая детям исследовать окружающие его предметы-носители величин на возможность их использования в качестве мерки.
Введение однозначных, а затем и многозначных чисел в разных системах счисления опирается на спроектированную жизненную ситуацию, а исторический аспект числа служит предметом исследования, а не наоборот, как это сделано у других авторов. При таком подходе ребенку не придется при раскрытии понятия отказываться от своего дошкольного опыта.
-При введении дей-я сложения (вычитания) многознач. чисел в разн. сист. счисл-я послед-но рассматр-ся этапы его выполнения:
1)прикидка: дети определяют, ничего не вычисляя, в каких разрядах будет «переполнение» (переход через разряд), а в каких нет (для вычитания это «разбиение» разрядов);
2) определение кол-ва цифр в результате вып-я действия (в традиц. прогр. это делается лишь при делении многозначных чисел);
3)опред-е цифры в кажд. разряде, что приводит детей к мысли о необх-ти констр-я таблицы сложения (вычитания).
-Введение десятичных дробей раньше обыкновенных (но после изучения всех действий с любыми многозначными числами) принципиально отличает данный курс от других. Это позволяет не только заново осмыслить принцип образования любого многозначного числа в любой системе счисления, но и значительно сократить время на выполнение действий с натуральными числами за счет конструирования действий с десятичными дробями. Действия с натуральными числами становятся средством для действий с дробями и глубже осознаются в том новом качестве.
-Следующей отличительной особенностью является подход к обучению решению задач. В 1-3-м классах дети не решают задачи по действиям. Решение записывается либо равенством, либо уравнением, но и то, и другое составляется с опорой на схему.
Источник: studfile.net
Рабочая программа по математике 1 класс Моро
Рабочая программа по математике «Школа России» 1 класс.
Вы уже знаете о суперспособностях современного учителя?
![]()
Тратить минимум сил на подготовку и проведение уроков.
![]()
Быстро и объективно проверять знания учащихся.
![]()
Сделать изучение нового материала максимально понятным.
![]()
Избавить себя от подбора заданий и их проверки после уроков.
![]()
Наладить дисциплину на своих уроках.
![]()
Получить возможность работать творчески.
Просмотр содержимого документа
«Рабочая программа по математике 1 класс Моро»
Пояснительная записка
Примерная основная образовательная программа начального общего образования. Программа разработана на основе Федерального государственного образовательного стандарта начального общего образования, Концепция духовно – нравственного развития и воспитание личности гражданина России, планируемых результатов начального общего образования.
Обучение математике является важнейшей составляющей начального общего образования. Этот предмет играет важную роль в формировании у младших школьников умения учиться.
Начальное обучение математике закладывает основы для формирования приёмов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно-следственные связи, закономерности, выстраивать логические цепочки рассуждений.
Изучая математику, они усваивают определённые обобщённые знания и способы действий. Универсальные математические способы познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий.
Универсальные учебные действия обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учиться.
Усвоенные в начальном курсе математики знания и способы действий необходимы не только для дальнейшего успешного изучения математики и других школьных дисциплин, но и для решения многих практических задач во взрослой жизни.
Основными целями начального обучения математике являются:
- математическое развитие младших школьников;
- формирование системы начальных математических знаний;
Место курса в учебном плане. На изучение математики в каждом классе начальной школы отводится по 4 часа в неделю. Курс рассчитан на 540ч: в 1 классе 132ч (33 учебные недели), во2 – 4 классах – по 136 ч(34 учебные недели). Программа также может осуществляться, когда на изучение предмета отводится 5 часов в неделю.
При увеличении количества часов на изучение предмета, часть формируемая участниками образовательного процесса, использована на расширение и углубление базы. Это способствует качеству обучения и достижению более высокого уровня как предметных, так и личностных и метапредметных результатов обучения. На изучение курса в 1 классе отводится по плану: 132ч, по факту:129ч ( праздничные дни – 04.11.2016г., 01.05.2017г., 09.05.2017г.)
Результаты изучения курса Программа обеспечивает достижение выпускниками начальной школы следующих личностных, метапредметных и предметных результатов.
Предметные результаты — Использование приобретённых математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также для
оценки их количественных и пространственных отношений. — Овладение основами логического и алгоритмического мышления,
пространственного воображения и математической речи, основами счёта, измерения, прикидки результата и его оценки, наглядного представления данных в разной форме (таблицы, схемы, диаграммы), записи и выполнения алгоритмов. — Приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач. — Умения выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, выполнять и строить алгоритмы и стратегии в игре, исследовать, распознавать и изображать геометрические фигуры, работать с таблицами, схемами, графиками и диаграммами, цепочками, представлять, анализировать и интерпретировать данные. — Приобретение первоначальных навыков работы на компьютере (набирать текст на клавиатуре, работать с меню, находить информацию по заданной теме, распечатывать её на принтере).
СОДЕРЖАНИЕ КУРСА
Числа и величины Счёт предметов. Образование, название и запись чисел от 0 до 1 000 000. Десятичные единицы счёта. Разряды и классы. Представление многозначных чисел в виде суммы разрядных слагаемых.
Сравнение и упорядочение чисел, знаки сравнения. Измерение величин. Единицы измерения величин: массы (грамм, килограмм, центнер, тонна); вместимости (литр), времени (секунда, минута, час, сутки, неделя, месяц, год, век). Соотношения между единицами измерения однородных величин. Сравнение и упорядочение однородных величин.
Доля величины (половина, треть, четверть, десятая, сотая, тысячная).
Арифметические действия Сложение, вычитание, умножение и деление. Знаки действий. Названия компонентов и результатов арифметических действий. Таблица сложения. Таблица умножения. Взаимосвязь арифметических действий (сложения и вычитания, сложения и умножения, умножения и деления). Нахождение неизвестного компонента арифметического действия.
Деление с остатком. Свойства сложения, вычитания и умножения: переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения и вычитания. Числовые выражения. Порядок выполнения действий в числовых выражениях со скобками и без скобок. Нахождение значения числового выражения.
Использование свойств арифметических действий и правил о порядке выполнения действий в числовых выражениях. Алгоритмы письменного сложения и вычитания многозначных чисел, умножения и деления многозначных чисел на однозначное, двузначное и трёхзначное число.
Способы проверки правильности вычислений (обратные действия, взаимосвязь компонентов и результатов действий, прикидка результата, проверка вычислений на калькуляторе). Элементы алгебраической пропедевтики.
Выражения с одной переменной вида a ± 28, 8 ∙ b, c : 2; с двумя переменными вида: a + b, а – b, a ∙ b, c : d (d ≠ 0), вычисление их значений при заданных значениях входящих в них букв. Использование буквенных выражений при формировании обобщений, при рассмотрении умножения 1 и 0 (1 ∙ а = а, 0 ∙ с = 0 и др.). Уравнение. Решение уравнений (подбором значения неизвестного, на основе соотношений между целым и частью, на основе взаимосвязей между компонентами и результатами арифметических действий).
Работа с текстовыми задачами Задача. Структура задачи. Решение текстовых задач арифметическим способом. Планирование хода решения задач. Текстовые задачи, раскрывающие смысл арифметических действий (сложение, вычитание, умножение и деление). Текстовые задачи, содержащие отношения «больше на (в) …», «меньше на (в) …».
Текстовые задачи, содержащие зависимости, характеризующие процесс движения (скорость, время, пройденный путь), расчёт стоимости товара (цена, количество, общая стоимость товара), расход материала при изготовлении предметов (расход на один предмет, количество предметов, общий расход) и др. Задачи на определение начала, конца и продолжительности события. Задачи на нахождение доли целого и целого по его доле. Решение задач разными способами. Представление текста задачи в виде рисунка, схематического рисунка, схематического чертежа, краткой записи, в таблице, на диаграмме.
Пространственные отношения. Геометрические фигуры Взаимное расположение предметов в пространстве и на плоскости (выше — ниже, слева — справа, за — перед, между, вверху — внизу, ближе — дальше и др.).
Распознавание и изображение геометрических фигур: точка, линия (прямая, кривая), отрезок, луч, угол, ломаная; многоугольник (треугольник, четырёхугольник, прямоугольник, квадрат, пятиугольник и т. д.). Свойства сторон прямоугольника. Виды треугольников по углам: прямоугольный, тупоугольный, остроугольный.
Виды треугольников по соотношению длин сторон: разносторонний, равнобедренный (равносторонний). Окружность (круг). Центр, радиус окружности (круга). Использование чертёжных инструментов (линейка, угольник, циркуль) для выполнения построений. Геометрические формы в окружающем мире.
Распознавание и называние геометрических тел: куб, пирамида, шар.
Геометрические величины Геометрические величины и их измерение. Длина. Единицы длины (миллиметр, сантиметр, дециметр, метр, километр). Соотношения между единицами длины. Перевод одних единиц длины в другие. Измерение длины отрезка и построение отрезка заданной длины. Периметр.
Вычисление периметра многоугольника, в том числе периметра прямоугольника (квадрата). Площадь. Площадь геометрической фигуры. Единицы площади (квадратный миллиметр, квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный километр). Точное и приближённое (с помощью палетки) измерение площади геометрической фигуры.
Вычисление площади прямоугольника (квадрата).
Работа с информацией Сбор и представление информации, связанной со счётом (пересчётом), измерением величин; анализ и представление информации в разных формах: таблицы, столбчатой диаграммы. Чтение и заполнение таблиц, чтение и построение столбчатых диаграмм. Интерпретация данных таблицы и столбчатой диаграммы.
Составление конечной последовательности (цепочки) предметов, чисел, числовых выражений, геометрических фигур и др. по заданному правилу. Составление, запись и выполнение простого алгоритма (плана) поиска информации. Построение простейших логических высказываний с помощью логических связок и слов («верно/неверно, что …», «если …, то …», «все», «каждый» и др.).
Учебно – тематический план
| № | Раздел | часов |
| 1. | Подготовка к изучению чисел. Пространственные и временные представления | 8 ч |
| 2. | Числа от 1 до 10. Число 0 Нумерация. | 28ч |
| 3. | Числа от 1 до 10. Сложение и вычитание | 28ч |
| 4. | Числа от 1 до 20. Сложение и вычитание (продолжение) | 28 ч |
| Числа от 1 до 20. Нумерация | 12ч | |
| 5. | Числа от 1 до 20. Сложение и вычитание (продолжение) | 22 ч |
| 6. | Итоговое повторение «что узнали, чему научились в 1 классе» | 5ч |
| 7 | Проверка знаний | 1ч |
- ценить и принимать следующие базовые ценности: «добро», «терпение», «родина», «природа», «семья», «мир», «настоящий друг», «справедливость», «желание понимать друг друга», «понимать позицию другого»;
- уважение к своему народу, к другим народам, терпимость к обычаям и традициям других народов;
- освоение личностного смысла учения; желания продолжать свою учебу;
- любознательность; способность самостоятельно действовать, а в затруднительных ситуациях обращаться за помощью к взрослому; принимать заинтересованное участие в образовательном процессе;
- оценка жизненных ситуаций и учебных текстов с точки зрения общечеловеческих норм, нравственных и этических ценностей;
- уважительное отношение к ответу товарища, принятие разных способов решения, оказание помощи товарищу в поиске допущенной ошибки;
- умение видеть эстетическую и практическую привлекательность математических объектов (строение числовых последовательностей, геометрических фигур, нахождение периметра и площади прямоугольника из предметов ближайшего окружения);
- умение ориентироваться в первоначальной математической терминологии, «подчиняться» математическим законам и правилам для достижения успешного результата;
- умение видеть и принимать в текстах задач информацию о профессиональной деятельности людей, ценности труда, истории российских городов.
Метапредметные результаты обучающихся. К концу учебного года будут сформированы:
Источник: kopilkaurokov.ru
ПРОГРАММА МОРО и ИСТОМИНА
Подготовка младших школьников к введению типовых задач с пропорциональными величинами. Формирование у учащихся первых представлений о пропорциональной зависимости величин. Какие методические приемы может использовать учитель с этой целью? Проанализируйте альтернативные учебники математики для начальных классов и приведите примеры различных упражнений, используемых для ознакомления учащихся с тройками величин и зависимостями между ними. Какой методический подход вам показался наиболее интересным и почему?
Все составные задачи в курсе математики начальных классов можно условно поделить на две группы.
Составные задачи
| Типовые | Нетиповые |
| -На нахождение четвертого пропорционального -На пропорциональное деление или на нахождение неизвестного по двум суммам -На нахождение неизвестного по двум разностям -На движение | Все остальные задачи, которые не подходят ни под один из типов, называют нетиповыми. Их классифицируют по видам простых задач, входящих в них. |
При решении типовых задач учащиеся знакомятся с тройками пропорциональных величин. Их решение позволяет осуществлять пропедевтику понятий «прямая и обратная пропорциональная зависимость», которые будут изучаться в средней школе.
В начальных классах такая терминология не вводиться, мы говорим лишь о тройках пропорциональных величин, учим детей выделять их в задаче и разбираем, как эти величины взаимосвязаны.
В каждой из троек величин выделяют:
1) единицу – т.е. величину, которая повторяется несколько раз;
2) количество повторений единицы;
3) общее значение величины.
Детей знакомят с такими основными тройками, как:
• Цена – количество – стоимость;
• Масса одного предмета – количество предметов – общая масса;
• Емкость (объем) одного сосуда – количество сосудов – общая емкость (объем);
• Расход ткани на 1 вещь – количество вещей – общий расход ткани;
• Выработка в единицу времени (производительность) – время работы – общая выработка;
• Скорость – время – расстояние;
• Длина – ширина – площадь
Кроме этих троек величин в задачах встречаются и другие. Например:
Количество клубков на 1 свитер – количество свитеров – общее количество клубков.
С этими тройками величин учащиеся начинают знакомиться в 3 классе при изучении темы «умножение и деление».
Взаимосвязи между величинами в тройке отражается в трех видах простых задач:
1. Нахождение общей величины (умножение);
2. Нахождение единицы (деление);
3. Нахождение количества (деление).
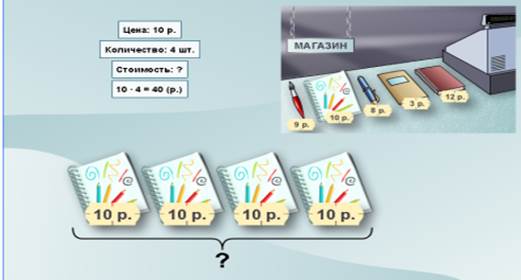
На подготовительном этапе в 3 классе учащихся начинают знакомить с этими тройками величин. Обычно в качестве первой берут тройку «цена – количество – стоимость». Организуют дидактическую игру «в магазин» (канцелярский). Учитель выставляет у доски «товар» и на каждый предмет прикрепляет ценник. Разыгрывают ситуации, в процессе которых вводят понятие «цена» — стоимость одного товара, «количество» — сколько предметов купили, «стоимость» — сколько денег заплатили.
Составляем тройки взаимообратных задач и учимся их записывать кратко в таблицу.
| Цена | Количество | Стоимость |
| 2 р. | 4 шт. | ? |
| ? | 4 шт. | 8 р. |
| 2 р. | ? | 8 р. |
Таким же образом вводят и другие тройки величин на других уроках (1 тройка величин -1 урок).
При введении лучше использовать практическую работу.
На подготовительном этапе учащиеся должны научиться решать простые задачи с тройками величии разного рода.
Позднее из этих простых задач составляют составные нетиповые задачи в два действия. Например: Мама купила 3 пакета муки по 2 килограмма в каждом и 1 кг яблок. Какова масса всей покупки?
Эту задачу можно разделить на 2 простых.
1 задача – на нахождение общей массы муки с тройкой величин.
2 задача – на нахождение суммы двух величин.

ПРОГРАММА МОРО и ИСТОМИНА
М3И ч2 стр 40-41
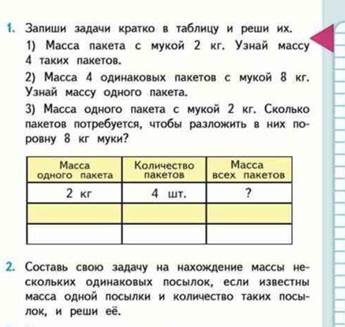
Масса одного предмета-количество предметов-общая масса
Емкость (объем) одного сосуда – количество сосудов – общая емкость (объем);
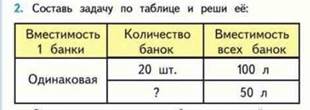
• Расход ткани на 1 вещь – количество вещей – общий расход ткани;
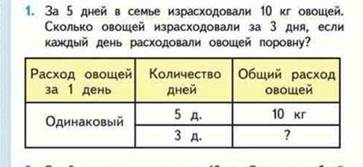
• Выработка в единицу времени (производительность) – время работы – общая выработка;

М3Мч2 стр 17 номер 4
• Скорость – время – расстояние;
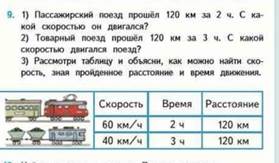
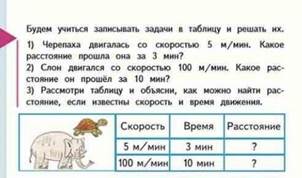
• Длина – ширина – площадь
Сделайте сравнительный анализ альтернативных учебников математики (программы М.И.Моро и Н.Б.Истоминой) и выясните, с какими видами задач на нахождение 4-го пропорционального знакомят учащихся начальных классов по различным программам. Какова последовательность их введения? Когда они появляются в учебнике впервые? Проведите анализ учебников по двум программам. Для выбранных задач составьте таблицы.
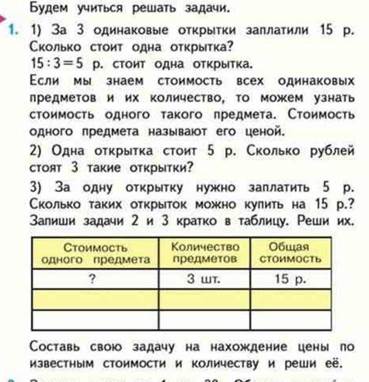
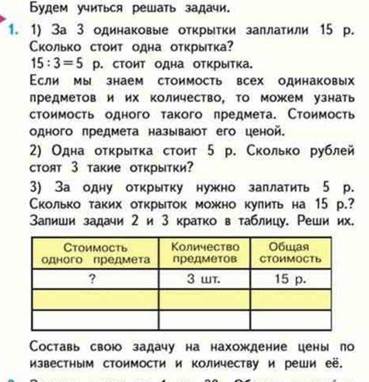
| Цена | Количество | Стоимость | |
| 1 откр 2 откр | одинаковая | 3 шт 1 шт | 15 р ? |

М3Мч1 стр 61 номер 7
| Расход ткани на 1 м | Количество вещей | Общий расход ткани |
| одинаковое | 8 шт ? | 24 м 15 м |
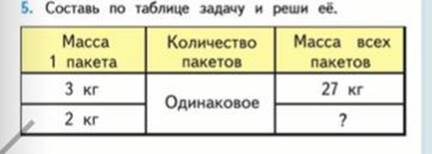

М4Мч1 стр 87
| Расход ткани на 1 м | Количество вещей | Общий расход ткани | |
| Детские платья Взрослые платья | 2 м ? | 32 шт 16 шт | одинаковый |
Методика их изучения по программе Моро М.И. такая: каждый вид вводят по очереди в три этапа: подготовка, ознакомление и формирование умения решать такие задачи.
Но анализ учебников показывает, что не все 6 видов есть в учебнике. Есть специальные уроки для введения 1 и 2 видов (М4М ч.1 с.86), можно найти задачи 3 и 4 видов. Хотя их введение специальными уроками в учебнике не предусмотрено. Нет задач 5 и 6 видов, следовательно, учитель сам продумывает тематический план их введения и, если класс сильный, можно рассмотреть все 6 видов, если слабый, то первые 4 вида. Решаем эти задачи с различными тройками величин.
Проанализируйте учебники математики для начальных классов по программам М.И.Моро и Н.Б.Истоминой и приведите примеры различных видов типовых задач на нахождение неизвестного по двум суммам (на пропорциональное деление) и по двум разностям. Какова последовательность введения различных видов этих задач в учебниках М.И. Моро, И.И. и Н.Б. Истоминой.
Когда они появляются в учебнике впервые? Для выбранных задач составьте таблицы.
Задания на нахождение неизвестного по двум суммам

| Цена | Количество | Стоимость |
| 1 кусок 2 кусок | одинаковая | 5 м 4 м |

| Масса одного предмета | Количество предметов | Общая масса |
| 1 мешок 2 мешок | ? Одинаковая ? | 56 кг 24 кг |
Задание на нахождение неизвестного по двум разностям
| Расход ткани на 1 вещь | Количество вещей | Общий расход ткани | |
| 1 кусок 2 кусок | Одинаково | ? ? на 2 больше | 6 м 10 м |
| Масса одного предмета | Количество предметов | Общая масса | |
| 1 столовая 2 столовая | Одинаковая | 5 шт 2 шт | ? на 24 кг больше ? |
Методика работы с задачами этого типа, такая же, как и с задачами предыдущего типа, т.е. все виды вводят по очереди и отрабатывают на различных тройках величин, но анализ учебников по программе М.И.Моро 4 класс показывает, что эта схема выполняется не полностью. Есть специальные уроки, где вводят задачи 1 и 2 видов (М4М ч.2 с. 46), а введение остальных видов не предусмотрено. Но учитель может предусмотреть это сам. Для сильного класса возможно введение 6 видов, а для слабого достаточно 2 видов.
Источник: poisk-ru.ru