Модели надежности ПО служат для предсказания значений метрик, позволяющих оценить надежность на различных этапах тестирования программного продукта. Например, в том случае, если к некоторому моменту тестирования количество обнаруженных и исправленных ошибок уже достаточно велико, это может создать впечатление, что тестирование продукта близится к завершению, то есть ошибок в программе осталось немного. Однако, это может совершенно не соответствовать действительности, и как раз использование моделей надежности программ может помочь прояснить подобную ситуацию.
Математические модели надежности программ можно разбить на группы по следующим признакам:
· Вид «функции риска», определяющей временную структуру появления ошибок в программе;
· Сложность разработки программы;
· Способы «посева» ошибок и оценки числа исходных ошибок по соотношению исходных и внесенных;
· Сравнение числа успешных прогонов программы и общего числа прогонов для различных структур пространства входных данных.
1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия…
Модели, основанные на использовании функции риска
Модель Джелинского-Моранды.
Это одна из первых и простейших моделей классического типа, послужившая основой для дальнейших разработок в этом направлении. Модель была использована при разработке таких значительных программных проектов, как программа Аполло (некоторых ее модулей). Модель Джелинского-Моранды основана на следующих предположениях:
1. Интенсивность обнаружения ошибок R(t) пропорциональна текущему количеству ошибок в программе, то есть изначальному количеству ошибок за вычетом количества ошибок, уже обнаруженных на данный момент.
2. Все ошибки в программе равновероятны и не зависят друг от друга.
3. Все ошибки имеют одинаковую степень важности.
4. Время до следующего отказа программы распределено экспоненциально.
5. Исправление ошибок происходит без внесения в программу новых ошибок.
6. R(t) = const в промежутке между любыми двумя соседними моментами обнаружения ошибок.
Согласно этим предположениям, функция риска будет представлена как:
В этой формуле t – это произвольный момент времени между обнаружением (i-1)-й и i-й ошибок; K – неизвестный коэффициент масштабирования; B – начальное количество оставшихся в программе ошибок (также неизвестное). Таким образом, если в течении времени t было обнаружено (i-1) ошибок, это означает, что в программе еще остается B-(i-1) необнаруженных ошибок. Полагая, что
и используя предпосылку 6, а также равенство (13.2), можно заключить, что все Xi имеют экспоненциальное распределение
и плотность вероятности отказа, соответственно, равна
Тогда функцию правдоподобия (согласно предпосылке 2) можно записать как
или, переходя к логарифму функции правдоподобия, имеем
Максимум функции правдоподобия можно найти, используя следующие условия
Из формулы (13.3) получается оценка максимального правдоподобия для K
Подставляя выражение (13.5) в (13.4), находим нелинейное уравнение для вычисления –оценки максимального правдоподобия для B
Математическое моделирование и вычислительная математика — Александр Шапеев
Это уравнение можно упростить перед тем, как искать его решение, если записать его с использованием следующих обозначений
Поскольку имеют смысл лишь целочисленные значения , функции из выражения (13.7) можно рассматривать только для целочисленных аргументов. Более того, , поскольку n ошибок с программе уже обнаружено. Таким образом, оценка максимального правдоподобия для B может быть получена с помощью вычисления начальных значений функций fn(m) и gn(m) для m=n+1, n+2…, и анализа разницы |fn(m)-gn(m)|.
Поскольку правая и левая части выражения (13.7) одинаково монотонны, это порождает проблему единственности решения, а также проблему его существования. Конечное решение в области существует тогда и только тогда, когда выполняется неравенство
В противном случае оценка максимального правдоподобия будет Условие (13.8) можно переписать в более удобном виде
где A – то же самое выражение, что и в формуле (13.7). Необходимо отметить, что, A является интегральной характеристикой n встретившихся в программе за время тестирования ошибок, и представляет (в статистическом смысле) набор интервалов Xi между ошибками.
Рассмотрим пример использования модели Джелинского-Моранды, в котором она применяется к следующим экспериментальным данным: в течение 250 дней было обнаружено 26 ошибок, интервалы между обнаружением которых представлены в таблице 13.1. Для этих данных мы имеем n=26 и . Условие (13.9) выполняется, и, таким образом, оценка максимального правдоподобия имеет единственное решение. В таблице 13.2 представлены начальные значения функций, входящих в уравнение (13.7), для множества аргументов
Наилучшим решением для уравнения (13.7) является m=32 (соответствующая строка в таблице дает минимальное значение разницы функций по модулю, то есть максимально приближает ее к нулю, что нам и требуется), то есть = m-1=31. Из выражения (13.5) находим = 0.007.
Среднее время (время, оставшееся до обнаружения (n+1)-й ошибки) есть инвертированная оценка интенсивности для предыдущей ошибки:
В этом примере, , и время до полного завершения тестирования
Таблица 10. Интервалы между обнаружением ошибок.
| I | Xi | I | Xi | i | Xi | i | Xi |
Таблица 11. Значения функций.
| m | ||
| 3.854 | 2.608 | 1.246 |
| 2.891 | 2.371 | 0.520 |
| 2.427 | 2.172 | 0.255 |
| 2.128 | 2.005 | 0.123 |
| 1.912 | 1.861 | 0.051 |
| 1.744 | 1.737 | 0.007 |
| 1.608 | 1.628 | -0.020 |
| 1.496 | 1.532 | -0.036 |
Простая экспоненциальная модель.
Основное различие между этой моделью и моделью Джелинского-Моранды, рассмотренной в предыдущем разделе, в том, что эта модель не использует предположение 6, и, таким образом, допускает, что функция риска может меняться между моментами обнаружения ошибок, то есть она больше не является константой на этих интервалах. Пусть N(t) – число ошибок, обнаруженных к моменту времени, и пусть функция риска пропорциональна количеству ошибок, оставшихся в программе после момента t.
Продифференцируем обе части этого уравнения по времени:
Учитывая, что — это R(t) (количество ошибок, обнаруживаемых в единицу времени), получаем дифференциальное уравнение для R(t)
Если рассмотреть начальные значения N(0)=0, R(0)=KB, то решением уравнения (3.10) будет
Оценки параметров К и В можно получить аналогично модели Джелинского-Моранды и затем с помощью оценки функции риска можно спрогнозировать ситуацию на следующие этапы отладки.
Модель Шика-Уолвертона.
Эта модель основана на предположении, что функция риска пропорциональна не только количеству ошибок в программе, но и продолжительности процесса тестирования. Кроме того, предполагается, что чем дольше ПО тестируется, тем больше появляется шансов на обнаружение последующих ошибок, поскольку в процессе отладки некоторые участки программы «подчищаются», что облегчает ее дальнейшее тестирование.
Модель основана на следующих предположениях:
- Все ошибки в программе равновероятны и независимы друг от друга.
- Все ошибки считаются одинаково серьезными.
- Исправление ошибок происходит без внесения в программу новых ошибок.
Функция риска для данной модели:
В этой формуле Xi — время между моментом обнаружения (i-1)-й ошибки до текущего момента .
Вероятность безотказного функционирования программы на интервале Xi равна:
что дает плотность вероятности отказа
Эти модели являются обобщением моделей Джелинского-Моранды и Шика-Уолвертона. В отличие от этих моделей, модели Липова допускают более одной ошибки в интервале тестирования, и кроме того, допускают, что не все из ошибок, обнаруженных а этом интервале, могут быть исправлены. Первая модель Липова (обобщение модели Джелинского-Моранды) основана на следующих предположениях:
1. Все ошибки равновероятны и независимы друг от друга.
2. Все ошибки считаются одинаково серьезными.
3. Интенсивность обнаружения ошибок постоянна на всем интервале тестирования.
4. На i-том интервале тестирования обнаруживается ошибок, но только из них исправляется.
Последнее предположение значительно отличает данную модель от всех моделей, рассмотренных ранее. Таким образом, функция риска определяется следующим выражением: где — общее количество ошибок, исправленных к моменту времени , а — это время окончания i-го интервала тестирования (измеренное обычным способом или таймером процессора). Еще одно отличие данной модели от модели Джелинского-Моранды в том, что интервалы фиксированные, а не произвольные.
Вторая модель Липова (обобщение модели Шика-Уолвертона) основана на следующих предположениях. Интенсивность обнаружения ошибок пропорциональна текущему количеству ошибок в ПО и общему времени, затраченному на его тестирование, включая также «среднее» время поиска ошибки, обнаруженной на интервале тестирования. С учетом этих предположений, функция риска задается следующим выражением:
где — общее количество ошибок, исправленных к моменту времени . Формула (13.12) отличается от первой модели Липова вторым множителем — , отражающем изменение интервала тестирования.
Геометрические модели
В этом разделе рассмотрен пример геометрической модели, предложенной П. Б. Морандой и являющейся модификацией модели Джелинского-Моранды.
Модель основана на предположении, что начальное количество ошибок в программе B не является фиксированным значением (не ограничено), более того, не все ошибки встречаются с одинаковой вероятностью. Также предполагается, что чем дольше длится процесс отладки ПО, тем труднее становится обнаруживать в нем ошибки, и, таким образом, ПО никогда полностью не освобождается от ошибок. Основные предположения в этой модели следующие:
1. Общее количество ошибок в программе неограниченно;
2. Ошибки встречаются с разной вероятностью;
3. Процесс обнаружения ошибок не зависит от самих ошибок;
4. Интенсивность обнаружения ошибок изменяется по закону геометрической прогрессии, но между моментами обнаружения ошибок интенсивность постоянна.
Исходя из этих предположений, функцию риска можно записать следующим выражением:
где t – временной интервал между обнаружением (i-1)-ой и i-той ошибок. Начальное значение этой функции R(0) = D, и функция риска убывает со скоростью геометрической прогрессии (0
что приводит к убыванию шага изменения R(t) в процессе обнаружения ошибок. Таким образом, более поздние ошибки труднее обнаружить, и они оказывают меньшее влияние на уменьшение потока ошибок, чем предыдущие ошибки. Если снова положить (временной интервал между обнаружением (i-1)-ой и i-той ошибок), тогда, согласно второму и третьему предположению, Xi распределены экспоненциально с плотностью распределения
Эта модель не позволяет определить, сколько ошибок осталось в ПО, но с ее помощью можно найти его «уровень чистоты». “Уровень чистоты” — это отношение
Оценка максимального правдоподобия для этого значения будет
Модель Шнейдевинда
Эта модель основана на подходе, что чем позже встречаются ошибки, тем большее значение они имеют для процесса предсказания ошибок в программе. Предположим, что есть m интервалов тестирования, и пускай на i-том интервале обнаружено ошибок. Тогда возможно три различных подхода:
1. Использовать данные об ошибках на всех интервалах;
2. Не рассматривать данные об ошибках, обнаруженных на первых (s-1) интервалах, и использовать только данные с s-того по m-тый;
3. Использовать суммарное количество ошибок, обнаруженных с первого по (s-1)-ый интервал, т.е. , и отдельные ошибки с s-того по m-тый интервалы.
Подход 1 предлагается использовать в тех случаях, когда для предсказания будущего состояния ПО необходимы данные со всех интервалов тестирования. Подход 2 – когда есть причины полагать, что произошел некий перелом в процессе обнаружения ошибок, и только данные последних m – (s-1) интервалов имеет смысл учитывать в прогнозах на будущее. И наконец, подход 3 является компромиссом между первыми двумя подходами.
Модель основана на следующих предположениях:
1. Количество ошибок на интервале тестирования не зависит от количества ошибок на остальных интервалах;
2. Количество обнаруженных ошибок убывает от одного интервала к другому;
3. Все интервалы тестирования имеют одинаковую длину;
4. Интенсивность обнаружения ошибок пропорциональна количеству ошибок, содержащихся в программе в текущий момент времени.
Лекция 14. Модели, основанные на методе «посева» и разметки ошибок, и модели на основе учета структуры входных данных
Методы оценки надежности программ, основанные на моделях «посева» и разметки ошибок, рассмотрены на примере трех моделей: Милза, Бейзина и простой эвристической модели. Согласно методике, предложенной Милзом, программа изначально “засевается” известным количеством некоторых ошибок — M. Главное предположение модели в том, что «засеянные» ошибки распределены таким же образом, как и естественные ошибки программы, и, следовательно, вероятность обнаружения для «засеянной» ошибки такая же, как и для естественной. После этого начинается процесс тестирования ПО. Пусть во время тестирования было обнаружено (m+v) ошибок, из которых m ошибок было искусственно «засеяно», а v ошибок содержалось в ПО изначально. Тогда, согласно методу максимального правдоподобия, начальное количество ошибок в программе можно оценить следующим образом: .
Серьезным недостатком этой модели является предположение об одинаковости распределения сгенерированных и естественных ошибок, которое невозможно проверить, особенно на более поздних стадиях разработки ПО, когда многие простые ошибки (такие, как синтаксические ошибки, например) уже исправлены, и только наиболее сложные для обнаружения ошибки еще остаются в ПО.
Теперь рассмотрим модель Бейзина. Пусть программный продукт содержит Nk команд. Из этих Nk команд произвольно выбираются n команд, и в каждую из этих n команд заносится ошибка. После этого для тестирования случайным образом выбирается r команд. Если в процессе тестирования было случайным образом обнаружено m “засеянных” и v естественных ошибок, это означает, что, согласно методу максимального правдоподобия, начальное количество ошибок в программе можно оценить следующим образом:
где скобками ][ обозначена целая часть числа.
При использовании такой процедуры уровень пометки (т.е. среднее количество помеченных команд) должен превышать 20, чтобы полученную оценку можно было считать достаточно объективной. Эти процедуры могут применяться на любой стадии после того, как написание кода программы закончено.
Теперь рассмотрим простую эвристическую модель. Эта модель была предложена Б. Руднером. Она позволяет избавиться от главного недостатка модели Милза. Здесь тестирование производится параллельно, двумя независимыми группами разработчиков ПО.
Пусть и — количество ошибок, обнаруженных, соответственно, первой и второй группами, а — количество общих ошибок, то есть обнаруженных обеими группами, первой и второй. Начальное количество ошибок, содержащихся в программе, можно оценить, используя гипергеометрическое распределение и метод максимального правдоподобия
Источник: cyberpedia.su
Математические модели
Математические модели позволяют оценивать характеристики ошибок в программах и прогнозировать их надёжность при проектировании и эксплуатации. Модели имеют вероятностный характер, и достоверность прогнозов зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:
— показателей надёжности комплексов программ в процессе отладки;
— количества ошибок, оставшихся невыявленными;
— времени, необходимого для обнаружения следующей ошибки в функционирующей программе;
— времени, необходимого для выявления всех ошибок с заданной вероятностью.
В настоящее время предложен ряд математических моделей, основными из которых являются:
— экспоненциальная модель изменения ошибок в зависимости от времени отладки;
— модель, учитывающая дискретно — понижающуюся частоту появления ошибок как линейную функцию времени тестирования и испытаний;
— модель, базирующаяся на распределении Вейбула;
— модель, основанная на дискретном гипергеометрическом распределении.
При обосновании математических моделей выдвигаются некоторые гипотезы о характере проявления ошибок в комплексе программ. Наиболее обоснованными представляются предположения, на которых базируется первая экспоненциальная модель изменения ошибок в процессе отладки и которые заключаются в следующем:
1. Любые ошибки в программе являются независимыми и проявляются в случайные моменты времени.
2. интенсивность проявления ошибок при реальном функционировании программы зависит от среднего быстродействия ЭВМ.
3. Выбор отладочных тестов должен быть представительным и случайным
4. Ошибка, являющаяся причиной искажения результатов, фиксируется и исправляется после завершения тестирования либо вообще не обнаруживается.
Из этих свойств следует, что при нормальных условиях эксплуатации количество ошибок, проявляющихся в некотором интервале времени, распределено по закону Пуассона. В результате длительность непрерывной работы между искажениями распределена экспоненциально.
Предположим, что в начале отладки комплекса программ при τ = 0 в нём содержалось N0 ошибок. После отладки в течении времени τ осталось n0 ошибок и устранено n ошибок n0 + n = N0). При этом время τ соответствует длительности исполнения программ на вычислительной системе (ВС) для обнаружения ошибок и не учитывает простои машины, необходимые для анализа результатов и проведения корректировок. Интенсивность обнаружения ошибок в программе dn/dτ и абсолютное количество устранённых ошибок связываются уравнением
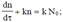
где k — коэффициент.
Время безотказной работы программ до отказа T или наработка на отказ, который рассматривается как обнаруживаемое искажение программ, данных или вычислительного процесса, нарушающее работоспособность, равно величине, обратной интенсивности обнаружения отказов (ошибок):
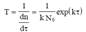
В процессе отладки и испытаний программ для повышения наработки на отказ от T1 до T2
необходимо обнаружить и устранить Δn ошибок. Величина Δn определяется соотношением:
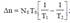
затрат времени Δτ на проведение отладки
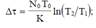
Вторая модель построена на основе гипотезы о том, что частота проявления ошибок (интенсивность отказов) линейно зависит от времени испытания ti между моментами обнаружения последовательных i — й и (i — 1) — й ошибок.
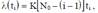
где N0 — начальное количество ошибок; K — коэффициент пропорциональности. Для оценки наработки на отказ получается выражение, соответствующее распределению Релея:
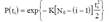
Отсюда плотность распределения времени наработки на отказ
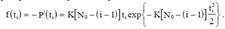
Особенностью третьей модели является учёт ступенчатого характера изменения надёжности при устранении очередной ошибки. В качестве основной функции рассматривается распределение времени наработки на отказ P(t). Если ошибки не устраняются, то интенсивность отказов является постоянной, что приводит к экспоненциальной модели для распределения:
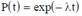
Отсюда плотность распределения наработки на отказ T определяется выражением:
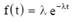
где t > 0, λ > 0 и 1/λ — среднее время наработки на отказ, т.е. Тср=1/λ. Здесь Тср – среднее время наработки на отказ.
Распределение Вейбулла достаточно хорошо отражает реальные зависимости при расчёте
функции наработки на отказ.
Основные понятия вероятности
Событие, вероятность события.


Частота или статистичская вероятность



Невозможные и достоверные события
Источник: mydocx.ru
МДК 4.2.. 9.-Конспекты-лекций.-МДК.4.2-ОКФКС-09.02.07_compressed. Конспект лекций по дисциплине мдк 04. 02 Обеспечение качества функционирования компьютерных систем

Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма

Скачать 0.51 Mb.
ЛЕКЦИЯ 4
Методы тестирования ПО
План.
1. Контрольный опрос
2. Тестирование: ручное и автоматизированное
3. Различные типы тестов
4. Как автоматизировать тесты
Есть множество разных типов тестов, которые вы можете применить, чтобы убедиться, что изменения в вашем коде работают по сценарию. Не все типы тестирования идентичны, хотя здесь мы рассмотрим, насколько основные практики тестирования отличаются друг от друга.
Сначала надо понять различия между ручными и автоматизированными тестами. Ручное тестирование проводится непосредственно человеком, который нажимает на кнопочки в приложении или взаимодействует с программным обеспечением или API с необходимым инструментарием. Это достаточно затратно, так как это требует от тестировщика установки среды разработки и выполнения тестов вручную. Имеет место вероятность ошибки за счет человеческого фактора, например опечатки или пропуска шагов в тестовом сценарии.
Автоматизированные тесты, с другой стороны, производятся машиной, которая запускает тестовый сценарий, который был написан заранее. Такие тесты могут сильно варьироваться в зависимости от сложности, начиная от проверки одного единственного метода в классе до отработки последовательности сложных действий в UI, чтобы убедиться в правильности работы. Такой способ считается более надежным, однако его работоспособность все еще зависит от того насколько скрипт для тестирования был хорошо написан.
Автоматизированные тесты – это ключевой компонент непрерывной интеграции
(Continuous Integration) и непрерывной доставки (continuous delivery), а также хороший способ масштабировать ваш QA процесс во время добавления нового функционала для
вашего приложения. Однако в ручном тестировании все равно есть своя ценность.
Поэтому в статье мы обязательно поговорим об исследовательском тестировании
(exploratory testing).
Различные типы тестов
Модульные тесты
Модульные тесты считаются низкоуровневыми, близкими к исходному коду вашего приложения. Они нацелены на тестирование отдельных методов и функций внутри классов, тестирование компонентов и модулей, используемых вашей программой.
Модульные тесты в целом не требуют особых затрат на автоматизацию и могут отрабатывать крайне быстро, если задействовать сервер непрерывной интеграции
(continuous integration server).
Интеграционные тесты
Интеграционные тесты проверяют хорошо ли работают вместе сервисы и модули, используемые вашим приложением. Например, они могут тестировать интеграцию с базой данных или удостоверяться, что микросервисы правильно взаимодействуют друг с другом. Эти тесты запускаются с бОльшими затратами, поскольку им необходимо, чтобы много частей приложения работало одновременно.
Функциональные тесты
Функциональные тесты основываются на требованиях бизнеса к приложению. Они лишь проверяют выходные данные после произведенного действия и не проверяют промежуточные состояния системы во время воспроизведения действия.
Иногда между интеграционными тестами и функциональными тестами возникают противоречия, т.к. они оба запрашивают множество компонентов, взаимодействующих друг с другом. Разница состоит в том, что интеграционные тесты могут просто удостовериться, что доступ к базе данных имеется, тогда как функциональный тест захочет получить из базы данных определенное значение, чтобы проверить одно из требований к конечному продукту.
Сквозные тесты (End-to-end tests)
Сквозное тестирование имитирует поведение пользователя при взаимодействии с программным обеспечением. Он проверяет насколько точно различные пользователи следуют предполагаемому сценарию работы приложения и могут быть достаточно простыми, допустим, выглядеть как загрузка веб-страницы или вход на сайт или в более сложном случае – подтверждение e-mail адреса, онлайн платежи и т.д.
Сквозные тесты крайне полезные, но производить их затратно, а еще их может быть сложно автоматизировать. Рекомендуется проводить несколько сквозных тестов, но все же полагаться больше на низкоуровневое тестирование (модульные и интеграционные тесты), чтобы иметь возможность быстро распознать серьезные изменения.
Приемочное тестирование
Приемочные тесты – это формальные тесты, которые проводятся, чтобы удостовериться, что система отвечает бизнес-запросам. Они требуют, чтобы приложение запускалось и работало, и имитируют действия пользователя. Приемочное тестирование может пойти дальше и измерить производительность системы и отклонить последние изменения, если конечные цели разработки не были достигнуты.
Тесты производительности
Тесты на производительности проверяют поведение системы, когда она находится под существенной нагрузкой. Эти тесты нефункциональные и могут принимать разную форму, чтобы проверить надежность, стабильность и доступность платформы. Например, это может быть наблюдение за временем отклика при выполнении большого количества запросов или наблюдение за тем, как система ведет себя при взаимодействии с большими данными.
Тесты производительности по своей природе проводить достаточно затратно, но они могут помочь вам понять, какие внешние факторы могут уронить вашу систему.
Дымовое тестирование (Smoke testing)
Дымовые тесты – это базовые тесты, которые проверяют базовый функционал приложения. Они отрабатывают достаточно быстро и их цель дать понять, что основные функции системы работают как надо и не более того. Такое тестирование направлено на выявление явных ошибок. Дымовые тесты могут оказаться полезными сразу после сборки нового билда для проверки на то, можете ли вы запустить более дорогостоящие тесты, или сразу после развёртывания, чтобы убедиться, что приложение работает нормально в новой среде.
Как автоматизировать тесты
Тестировщик может проводить все тесты, указанные выше, вручную, но это будет крайне затратно и непродуктивно. Поскольку люди имеют ограниченную возможность производить большое количество действий с повторениями при этом все еще проводя тестирование надежно. Однако машина может с легкостью воспроизводить эти же действия и проверить, допустим, что комбинация логин/пароль будет работать и в сотый раз без каких-либо нареканий. Для автоматизации тестирования, вам для начала придется написать их на каком-то из языков программирования с использованием фреймворка для тестирования, который подойдет для вашего приложения. PHPUnit , Mocha, RSpec – это примеры фреймворков для тестирования, которые вы можете использовать для PHP,
Javascript и Ruby, соответственно. В них есть множество возможностей для каждого языка, поэтому вам стоит немного позаниматься исследованием самостоятельно и проконсультироваться с сообществами разработчиков, чтобы понять, какой фреймворк подойдет вам лучше всего. Если ваши тесты могут запускаться с помощью скриптов из терминала, вы можете автоматизировать их, использовав сервер непрерывной интеграции по типу Bamboo или же облачного сервера Bitbucket Pipelines. Эти инструменты будут мониторить ваши репозитории и исполнять наборы тестов, как только новые изменения будут запушены в основной репозиторий. Если вы новичок в вопросах тестирования, обратитесь к нашему руководству по непрерывной интеграции, чтобы создать свой первый набор тестов.
Исследовательское тестирован
Чем больше функций и улучшений добавляется в ваш код, тем больше возрастает потребность в тестировании, поскольку на каждом этапе вам необходимо убеждаться, что система работает корректно. Также это понадобится каждый раз, когда вы исправляете баг, поскольку было бы не лишним убедиться, что он не вернется снова после нескольких релизов. Автоматизация – это ключ к тому, чтобы это стало возможным; написание тестов рано или поздно станет частью вашей практики разработчика.
Вопрос заключается в том, надо ли вообще в таком случае проводить ручное тестирование? Короткий ответ – да, и оно должно быть сфокусировано на том, что называется «исследовательское тестирование» (exploratory testing), которое помогает выявить неочевидные ошибки.
Сессия исследовательского тестирования не должна превышать двух часов и должна иметь четко ограниченную область действия, чтобы помочь тестировщикам сосредоточиться на определенной области программного обеспечения. После информирования всех тестировщиков о границах проведения тестирования, на их усмотрения остаются действия, которые они будут предпринимать, чтобы проверить, как поведет себя система. Такое тестирование является дорогостоящим по своей природе, но очень полезно для выявления проблем с пользовательским интерфейсом или проверки работоспособности сложных рабочих процессов для пользователей. Такое тестирование важно проводить всякий раз, когда в приложение добавляется кардинально новая функция, чтобы понять, как она поведет себя в пограничных условиях.
Контрольные вопросы:
1.
Чем отличается тестирование: ручное и автоматизированное?
2.
Назовите отличия различных типы тестов?
3.
Как автоматизировать тесты?
ЛЕКЦИЯ 5
Методы предотвращения угроз надежности
План.
1. Контрольный опрос
2. Автоматизация программирования
3. Введение избыточности
4. Типовые структуры данных
Большая трудоемкость и стоимость создания ПО систем управления заставляет уделять особое внимание обеспечению его надежной работы. Высокая стоимость ПО во многом обусловлена его низкой надежностью. Следует иметь в виду, что в настоящее время не разработаны методы проектирования программ с гарантированным отсутствием ошибок. Это объясняется рядом причин, и в том числе тем, что программное обеспечение значительно сложнее аппаратуры; характеризуется большей, чем аппаратура, зависимостью от применения; состоит из примитивных составляющих — машинных кодов, из которых синтезируются огромные программные структуры.
Однако накопленный опыт позволяет сформулировать принципы и метода проектирования программ, обеспечивающих их надежную, устойчивую работу, основные из которых показаны на рис. 5.4.1.
По образному выражению Ф.П. Брукса «программа — это сообщение, передаваемое человеком машине». Чтобы сделать это сообщение «понятным бессловесной машине», требуется предельная формализация как описания алгоритмов, так и программ.
1. Формализация позволяет в существенной степени исключить, а при наличии ошибок — облегчить их выявление и локализацию.
2.
Мощным средством повышения надежности у
ПО
САПР является автоматизация программирования, заключающаяся в использовании ЭВМ для составления машинных программ, т. е. программ, выполненных на языке ЭВМ по исходной программе, составленной на языке высокого уровня.
Системы автоматизированного программирования обеспечивают повышение производительности и облегчение труда программистов. Эти системы применяют для программирования языки высокого уровня, более близкие к естественному языку специалистов, и тем самым освобождают программиста от необходимости составлять программу на языке машинных команд. У нас в стране создан ряд систем автоматизированного программирования для ЭВМ. Эти системы обеспечивают
автоматизацию создания программ и документов с минимальным расходом ручного труда как при основных, так и при вспомогательных работах, в том числе: .трансляцию текстов программ в машинные коды с семантическим и синтаксическим контролем, автономную отладку программ, диалоговое общение программистов со средствами автоматизации, выпуск эксплуатационных и технологических документов, а также их корректировку.
Рис. 5. 4. 1. Классификация методов обеспечения надежной работы программного обеспечения
Эффективным методом повышения надежности ПО является введение избыточности, включающей программную, информационную и временную избыточность.
3. Программная избыточность применяет в комплексах ПО несколько вариантов программ, различающихся алгоритмами решения задачи или программной реализации одного и того же алгоритма.
3.
1.
Временная
избыточность использует часть производительности
ЭВМ для контроля исполнения программ и восстановления вычислительного процесса. Как следствие при проектировании ПО необходимо предусматривать резерв производительности ЭВМ, обычно резерв составляет 5-10%.
3.
2.
Информационная
избыточность заключается в резервировании
(дублировании) исходных и промежуточных данных, что обеспечивает как обнаружение искажения данных, так и устранение ошибок.
4. Структурное программирование позволяет облегчить проектирование и повысить надежность сложных программных комплексов.
Структурное программирование развилось на основе технологии процедурного и модульного программирования, а также блочно-иерархического подхода; представляет собой технологию программирования, построенную на совокупности определенных принципов и правил, среди которых прежде всего можно выделить модульность структуры, иерархию модулей, нисходящее проектирование.
5. Структурирование
данных позволяет уменьшить сложность комплекса программ и снизить вероятность появления ошибок из-за их неправильного использования. Совокупность данных можно разделить на два иерархических уровня: простые переменные и массивы. Простые переменные представляют собой минимальный компонент данных, имеющий имя и описание. Массивы образуются из нескольких
простых переменных по определенным правилам объединения и имеют собственное имя, описание и структуру.
С целью упорядочения создан ряд типовых структур данных, применение которых зависит от назначения и метода использования переменных. Структура массивов определяется на основе компромисса между объемом памяти для хранения массива и затратами производительности ЭВМ, необходимыми для выборочного поиска и обращения к данным в массиве. Так, простые структуры массивов экономны по затратам производительности ЭВМ для взаимодействия с данными, но требуют большого объема памяти. Для повышения надежности ПО целесообразно использовать простейшие структуры массивов данных,
Следует иметь в виду, что, как правило, устранение ошибок, обнаруженных в ПО, приводит к внесению новых ошибок, трудно обнаруживаемых, так как их последствия не проявляются на тестах. При проведении корректировок в комплексах программ необходим дополнительный анализ возможных последствий внесенных изменений. Любая корректировка ПО может быть сведена к трем типовым операциям: исключение части или всей подпрограммы; вставка компонентов или новой целой подпрограммы на имеющееся свободное место; замена части или всей подпрограммы в пределах освобождающегося свободного места или с расширением программы и использованием дополнительной памяти.
Контрольные вопросы:
1.
Что тактое автоматизация программирования?
2.
Что тактое введение избыточности?
3.
Что тактое типовые структуры данных?
ЛЕКЦИЯ 6
Математические модели описания статистических характеристик ошибок в программах.
План.
1. Контрольный опрос
2. Предназначение математических моделей;
3. Первая группа допущений;
4. Вторая группа допущений;
5. Третья группа допущений.
Детальный анализ проявления ошибок показывает их глубокую связь с методами структурного построения программ, типом языка программирования, степенью автоматизации технологии проектирования и многими другими факторами.
Статистические характеристики различных типов ошибок трудно описать математическими моделями, и более доступны для математического описания обобщенные характеристики ошибок в комплексе программ. Путем анализа и обобщения экспериментальных данных реальных разработок предложено несколько математических моделей, описывающих основные закономерности изменения суммарного количества
вторичных ошибок в программах. Модели имеют вероятностный характер, и достоверность прогнозов в значительной степени зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:
1. надежности функционирования комплекса программ в процессе отладки, испытаний и эксплуатации;
2. числа ошибок, оставшихся невыявленными в анализируемых программах;
3. времени, требующегося для обнаружения следующей ошибки в функционирующей программе;
4. времени, необходимого для выявления всех ошибок с заданной вероятностью.
Точное определение полного числа невыявленных ошибок в комплексе программ прямыми методами измерения невозможно. Однако имеются пути для приближенной статистической оценки их полного числа или вероятности ошибки в каждой команде программы. Такие оценки базируются на построении математических
Моделей в предположении о жесткой корреляции между общим количеством и проявлениями ошибок в комплексе программ после его отладки в течение времени T, т. е. между:
суммарным количеством первичных ошибок в комплексе программ (n
) или вероятностью ошибки в каждой команде программы (p
);
количеством ошибок, выявляемых в единицу времени в процессе тестирования и отладки при постоянных усилиях на ее проведение
интенсивностью искажений результатов в единицу времени () на выходе комплекса программ вследствие невыявленных первичных ошибок при функционировании программ.
Наиболее доступно для измерения количество вторичных ошибок в программе, выявляемых в единицу времени в процессе отладки. Возможна также непосредственная регистрация отказов и наиболее крупных искажений результатов, выявляемых средствами оперативного контроля в процессе функционирования программ. Все три показателя связаны некоторыми коэффициентами пропорциональности, значения которых зависят, в частности, от интервала времени, на котором производится сопоставление, от быстродействия ЭВМ, от эффективности средств автоматизации отладки и от некоторых других параметров. При фиксированных условиях разработки и функционирования конкретного комплекса программ эти коэффициенты имеют вполне определенное значения. Для другой подобной системы коэффициенты могут несколько измениться, однако оценки, полученные для нескольких конкретных систем, позволяют прогнозировать эти характеристики, а следовательно, и соответствующие показатели надежности ПС в зависимости от длительности отладки и ряда других факторов.
Описаны несколько математических моделей, основой которых являются различные гипотезы о характере проявления вторичных ошибок в программах. Эти гипотезы в той или иной степени апробированы при обработке данных реальных разработок, и их можно разделить на три группы. В
Источник: topuch.com