Урок 13
Информационное моделирование на компьютере
— Разновидности компьютерных моделей.
— Компьютерная математическая модель и вычислительный эксперимент.
— Имитационное моделирование.




Основные темы параграфа:
— вычислительные возможности компьютера;
— для чего нужны математические модели;
— компьютерная математическая модель;
— что такое вычислительный эксперимент;
— управление на основе моделей;
— имитационное моделирование.
Вычислительные возможности компьютера
Современным инструментом для информационного моделирования является компьютер. Конечно, на компьютере можно писать тексты (строить вербальные модели), рисовать карты и схемы (графические модели), строить таблицы (табличные модели). Но при таком использовании компьютера в моделировании его возможности проявляются не в полной мере.
Математическая модель. Видеоурок по алгебре 7 класс
Для моделирования на компьютере главной является его способность к быстрому счету. Современные компьютеры считают со скоростями в сотни тысяч, миллионы и даже миллиарды операций в секунду.
Учитывая, что расчеты производятся над многозначными числами (10-20 десятичных цифр), вычислительные возможности компьютера феноменальны. Эти возможности проявляются, прежде всего, при компьютерном математическом моделировании.
Для чего нужны математические модели
Многие процессы, происходящие в природе, технике, экономических и социальных системах, описываются сложными математическими соотношениями. Это могут быть уравнения, системы уравнений, системы неравенств и пр., которые являются математическими моделями описываемых процессов.

Математическая модель — это описание моделируемого процесса на языке математики.
В прежние времена, до появления ЭВМ, ученые стремились создавать такие математические модели, которые можно было бы просчитать вручную или с помощью несложных вычислительных механизмов. Поэтому математические модели были относительно простыми. Но простая модель не всегда хорошо описывает процесс. Ошибка расчетов по такой модели может быть слишком большой и полностью обесценить результат.
Еще в XVIII-XIX веках ученые-математики начали изобретать методы решения таких математических задач, которые не удавалось решить точно, аналитически. Например, вы знаете, что квадратное уравнение всегда можно решить точно, а вот кубическое — уже не всегда. Такие методы называются численными методами. Они сводят решение любой задачи к последовательности арифметических операций.
Но эта цепочка арифметических вычислений может быть очень длинной. И чем точнее мы хотим получить решение, тем она длиннее.
7 класс, 3 урок, Что такое математическая модель
Может оказаться, что для решения сложной задачи численным методом ученому потребуется вся жизнь. А может и этого не хватить! И какой смысл, например, начинать расчет прогноза погоды на завтрашний день, если для этого потребуется несколько лет работы?
Компьютерная математическая модель
Появление компьютеров сняло эти проблемы. Стало возможным проводить расчеты сложных математических моделей за приемлемое время. Например, рассчитать погоду на завтрашний день до его наступления. Ученые перестали себя ограничивать в сложности создаваемых математических моделей, полагаясь на быстродействие компьютеров.

Компьютерная математическая модель — это программа, реализующая расчеты состояния моделируемой системы по ее математической модели.
Что такое вычислительный эксперимент

Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом. Говорят также: численный эксперимент.

Вычислительный эксперимент в некоторых случаях может заменить реальный физический эксперимент.
Впечатляющий пример использования такой возможности — прекращение испытаний ядерного оружия, которые сопровождались значительным экологическим ущербом. Благодаря очень точным математическим моделям и мощным компьютерам стало возможно просчитать все последствия, к которым приводит изменение в конструкции ядерной бомбы. Образно говоря, удалось «взорвать бомбу» внутри компьютера, ничего не разрушив.
Важным свойством компьютерных математических моделей является возможность визуализации результатов расчетов. Этим целям служит использование компьютерной графики.
Представление результатов в наглядном виде — важнейшее условие для их лучшего понимания. Например, результаты расчетов распределения температуры в некотором объекте можно представить в виде его разноцветного изображения: участки с самой высокой температурой окрасить в красный цвет, а с самой холодной — в синий. Участки с промежуточными значениями температуры окрашиваются в цвета спектра, равномерно переходящие от красного к синему (рис. 2.7).
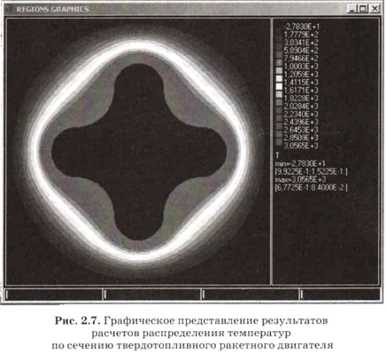
Для изображения изменяющихся со временем (динамических) результатов используют графическую анимацию.

Компьютерная графика позволяет человеку в процессе проведения численного эксперимента «заглянуть» в недоступные места исследуемого объекта. Можно получить изображение любого сечения объекта сложной формы с отображением рассчитываемых характеристик: температурных полей, давления и пр. В реальном физическом эксперименте такое можно сделать далеко не всегда. Например, невозможно выполнить измерения внутри работающей доменной печи или внутри звезды. А на модели это сделать можно.

Следующая страница Информационное моделирование на компьютере. Управление на основе моделей
Источник: xn—-7sbbfb7a7aej.xn--p1ai
Научная электронная библиотека


1. Понятие системы. Методы исследования систем. Система – это совокупность объектов, функционирующих и взаимодействующих друг с другом для достижения определённой цели. В ряде случаев проводить эксперименты можно на реальных системах. Однако далеко не всегда это возможно, например, при невозможности получения строгого математического описания системы.
Поэтому в таких случаях создаются модели реальных систем, которые и исследуются (слово «модель» происходит от греческого слова modulus). Выявленные в процессе исследования характеристики модели приписываются реальной системе, то есть системе-оригиналу. Исследования, проводимее на модели, и называются моделированием [9, 48, 62 и др.].
2. Общие определения модели и моделирования. Отметим: никакое определение не может в полном объёме охватить реально существующую деятельность по моделированию. Однако определения полезны тем, что в них делается попытка выделить наиболее существенные черты моделей и моделирования.
Свободная международная энциклопедия – википедия : Моделирование – исследование объектов познания на их моделях, построение и изучение моделей реально существующих предметов, процессов или явлений с целью получения объяснений этих явлений, а также для их предсказания.
Ляпунов А.А.: Моделирование – это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система ( модель ).
Советов Б.Я. и Яковлев С.А .: Модель – это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала [62].
3. Разновидности моделей. Модели принято делить на два класса: физические и математические. Физические модели имеют ту же физическую природу, что и оригинал.
Физической моделью является, например, аэродинамическая труба, в которой устанавливается самолёт для исследования поведения его органов управления при продувании трубы воздухом с такой же скоростью, как при реальном полёте. Физическим моделированием являются испытания опытных образцов различной аппаратуры на тряску, давление и т.д. Математическая модель – это точное или приближённое математическое описание свойств или закономерностей функционирования оригинала.
4. Определения математической модели и моделирования
Самарский А.А. и Михайлов А.П .: Математическая модель – это «эквивалент объекта, отражающий в математической форме важнейшие его свойства – законы , которым он подчиняется, связи, присущие составляющим его частям». « Математическое моделирование – процесс построения и изучения математических моделей реальных процессов и явле- ний» [61].
Севостьянов А.Г. : Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.
Скворцова М .: Математическая модель – это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная задача математического моделирования – не только исследовать эти объекты, но и предсказать результаты будущих наблюдений.
В целом в литературе довольно много похожих определений. Самое короткое и лаконичное определение модели дано в одной из зарубежных публикаций: Математическая модель это Уравнение , выражающее идею . Но это определение относится, скорее, к философскому понятию модели.
5. Немного истории. Исследование систем путем их моделирования. Ещё во 2-м веке до н.э. появилась геоцентрическая система (модель) мира Птоломея, затем − гелиоцентрическая система (модель) мира Николая Коперника (16-й век н.э., helio – приставка, означающая солнце).
С развитием техники перед изготовлением паровых машин, электрических установок, средств автоматизации вычислений и т.д. в большинстве случаев они предварительно отрабатывались на их моделях. Предварительное моделирование особенно важно проводить при разработке новых перспективных производственных технологий для обеспечения их эффективности, сложной и дорогостоящей техники для обеспечения её надежности (например, надёжности нового космического корабля) и т.д.
В 20-м веке с появлением ЭВМ активизировались разработка математических моделей и методов и технологий математического моделирования на ЭВМ. При этом установилась классификация способов исследования систем с помощью моделей [48, 62 и др.], приведённая на рис. В.1.
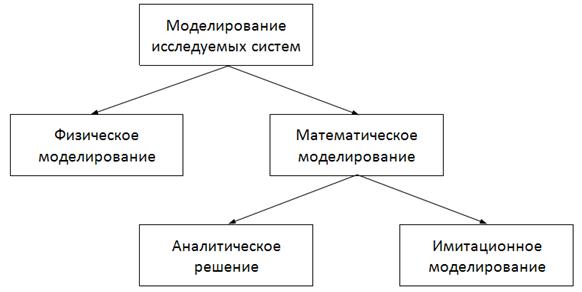
Рис. В.1. Способы исследования систем
В отличие от физического моделирования, предполагающего измерение соответствующих характеристик модели, математическое моделирование предполагает разработку математического описания функционирования исследуемой системы, которое в ряде случаев может иметь аналитическое решение. При имитационном моделировании на основе алгоритмов, описывающих указанное функционирование, модель воспроизводит процессы, происходящие в реальной системе. Частным случаем этого моделирования является эволюционное моделирование, связанное с исследованием эволюции различных систем [57].
6. Понятия функциональной полноты и адекватности модели. Пусть некоторый оригинал (рис. В.2) имеет k входов, на которые поступают соответствующие входные величины, задаваемые вектором X = ( X 1, X 2, … Xk ). Аналогично выходы оригинала задаются вектором Y = ( Y 1, Y 2, … Yk ).
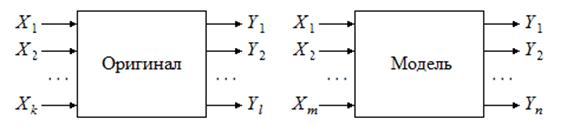
Рис. В.2. Абстрактная система оригинал – модель
Каждая координата Yi является функцией вектора X и внутреннего состояния оригинала. Последнее в общем случае может изменяться под воздействием как входных, так и выходных величин. Если на вход модели поступает последовательность векторов X, то имеют место векторные процессы X(t) и Y(t), которые могут быть детерминированными или случайными.
Как и оригинал, модель может иметь k входов и l выходов, формируе-мых 0 аналогично 0 оригиналу. Такая модель называется функционально полной. Если при этом имеет место ещё 0 и 0 полное 0 совпадение выходных процессов модели и её оригинала, соответствующих любому входному процессу, то говорят, что модель адекватна оригиналу.
Однако во многих случаях при моделировании нет необходимости воспроизводить все возможности оригинала. В этом случае выбирают m < k и n < l и нередко говорят о степени адекватности построенной модели по отношению к оригиналу. Однако заметим, что понятие «степень адекватности», а также используемые в литературе такие характеристики этой степени как «высокая степень адекватности», «достаточно адекватная» или «относительно адекватная», количественно не определены. Поэтому с математической точки зрения они несостоятельны. Использование же их объясняется тем, что нередко адекватность модели оригиналу просто невозможно проверить (например, ввиду ограниченности технических возможностей и т.д.).
Основные эт ап ы разработки математических моделей:
· Разработка математического описания предварительного варианта модели (уточнение задачи моделирования, определение требований к входным и выходным переменным, построение структурной схемы модели, выбор её параметров, выбор методов получения конечных и промежуточных результатов). Результатом этого этапа является формальное математическое описание блоков модели. При этом как бы исчезает физическая сторона исследуемой задачи, то есть для лиц, не знакомых с решаемой задачей, по математическому описанию модели крайне затруднительно или даже невозможно уяснить сущность этой задачи.
style=font-family:Symbol>· Разработка машинной программы моделирования, включая алгоритмизацию математического описания, разработку программы в соответствующей среде программирования и проверку правильности её работы (например, по моделированию характерных частных вариантов входных величин, для которых известны или могут быть рассчитаны значения выходных величин).
· Испытания и корректировка модели (моделирование исследуемой системы для известных частных случаев, сравнение получаемых при этом результатов с известными результатами и в случае необходимости – корректировка параметров модели). Данный этап часто называют интерпретацией результатов моделирования.
Разработка модели при отсутствии оригинала. Примером такой модели может служить модель интегральных показателей (ИП) здоровья населения, использующая в качестве параметров показатели здоровья населения. Эти показатели ежегодно определяются и публикуются Госкомстатом России. Основным вариантом таких моделей является следующий [42]:
где KI – весовые коэффициенты, ОКР – общий коэффициент рождаемости (число родившихся живыми младенцев, приходящихся на 1000 человек населения рассматриваемого региона), СППЖ – средняя продолжительность предстоящей жизни (значение прогноза, определяемого для поколения, родившегося в рассматриваемом году), ОЗО – общая заболеваемость по обращениям (число обращений населения в учреждения здравоохранения, приходящихся на 1000 человек населения), ОКС – общий коэффициент смертности (число умерших, приходящихся на 1000 человек населения), С – константа, позволяющая задавать среднее значение ИП для РФ в целом.
В приведённом выражении все ИП изменяются в интервале (0, 1), хотя это и не обязательно.
Факторный анализ на модели. Важной разновидностью исследуемых с помощью моделирования задач является факторный анализ. Его сущность заключается в исследовании влияния соответствующих параметров модели (факторов, входных факторов) на отклики (выходные факторы).
В зависимости от числа анализируемых факторов различают однофакторный, двухфакторный, … , многофакторный анализ. При проведении факторного анализа изменяют только рассматриваемый входной фактор, а значения остальных факторов либо не меняются вообще, либо изменяются только от эксперимента к эксперименту. В последнем случае получают семейство таблиц, в каждой строке которых приводятся значения откликов, соответствующих выбранным значениям рассматриваемого фактора. Причем каждая такая таблица составляется для различных значений остальных факторов.
Отметим, что в последние годы исследование математических моделей чаще всего проводят в среде программирования Delphi (см. приложение П1), которая позволяет значительно облегчить работу программистов по разработке программы моделирования и упростить технологию моделирования. Поэтому все рассматриваемые в монографии программные решения задач математического моделирования приводятся для среды Delphi .
В литературе имеется достаточно много публикаций, посвящённых различным вопросам построения математических моделей и непосредственно моделированию. Большинство их осталось за пределами монографии [3, 8, 19, 20, 30, 33, 39, 43, 47, 50, 54, 59, 60, 63, 69, 75 и др.]. Монография в основном нацелена на реализацию и исследование математических моделей в среде программирования Delphi .
Источник: monographies.ru
Знаковые модели. Компьютерные математические модели

В данном видеоуроке рассматриваются компьютерные математические модели и инструменты их реализации. Рассказывается о различных компьютерных математических моделях, их применении при решении задач, а также рассматриваются методы имитационного моделирования.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности

1. Откройте доступ ко всем видеоурокам комплекта.

2. Раздавайте видеоуроки в личные кабинеты ученикам.

3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ
Конспект урока «Знаковые модели. Компьютерные математические модели»
· Определение компьютерной математической модели.
· Использование компьютерной математических моделей.
· Применение при решении задач.
Самые разные математические модели широко использовались и используются при изучении многих научных областей и дисциплин. Так, на пример, учёные астрономы используют математические модели, чтобы предсказать движение небесных тел. Как мы уже знаем, при составлении любых информационных моделей учитываются существенные свойства объекта или явления. Но что делать, если этих свойств очень много или они очень сложны для расчёта? Ведь человеку понадобится немало времени для реализации такой математической модели.
Реализация – это расчёт состояния объекта или системы, по формулам из математической модели, которые связывают значения его исходных и результирующих параметров.
Это одна из важнейших областей применения компьютеров. Ведь компьютер способен выполнять миллионы математических операций в секунду.
Математические модели, реализованные на компьютере с помощью тех или иных программных средств, называются компьютерными математическими моделями.
Для реализации математических моделей на компьютере могут использоваться:
· различные языки программирования,
· различные математические пакеты.
При использовании некоторых средств визуализации можно наглядно представить результаты и процесс работы той или иной системы.
Компьютерные математические модели широко используются в различных областях науки. На пример, используя средства визуализации табличного процессора Microsoft Excel (его вы будете изучать позже) можно отобразить в виде линии траекторию полёта снаряда, который выпущен из пушки, расположенной на земле. Снаряд был выпущен с известной начальной скоростью, под определённым углом к горизонту.
Реализация математической модели в Microsoft Excel
После того, как математическая модель была задана достаточно нескольких нажатий клавиш, чтобы изменить исходные данные системы. И мы тут же получили результирующие данные для системы с другими параметрами.
Особую роль среди компьютерных математических моделей занимают модели систем, параметры которых могут принимать случайные значения в определённых пределах. Часто для того, чтобы оптимизировать работу такой системы, моделируют её работу при различных параметрах и находят их оптимальные значения. Такая математическая модель называется имитационной.
Имитационные модели применяются во многих сферах жизни человека. Например, моделирование системы обслуживания покупателей в магазине, чтобы выяснить, какое количество продавцов необходимо для нормальной его работы. Ведь мы не можем точно предсказать количество покупателей, пришедших в магазин за единицу времени или точное время обслуживания продавцом каждого из них.
Подобные модели могут применяться во многих областях науки. Рассмотрим пример из теории вероятности. Хорошо известно, что вероятность выпадения герба или цифры при подбрасывании монеты равна 50%, но как это проверить? Можно много раз подбросить монету, записывая результат. При этом очевидно, что чем большее число подбрасываний мы совершим, тем результат будет точнее.
Некоторые математики проделывали этот опыт. Результаты некоторые результаты представлены в таблице.
Исследователь
Количество опытов
Число выпадений герба
Источник: videouroki.net
Математическая модель программы что это
В статье рассмотрена общая концепция моделирования задач для последующего решения с использованием компьютера. Систематизированы этапы моделирования, и выделены их существенные особенности. Приведен практический пример моделирования и решения задачи.

В различных областях деятельности человека часто возникают задачи, в которых требуется описать реальные природные объекты и процессы, с целью изучения их свойств, структуры и законов развития, а так же их внутренних и внешних связей. Это необходимо знать для эффективного и результативного управления объектом или процессом, с одной стороны, и для наиболее точного и надежного прогнозирования, с другой стороны.
Описание реальных объектов и процессов в некоторых формальных терминах принято называть моделированием, а полученную абстракцию — моделью. Модели различают по способу их описания.
Например, вербальные модели (описание текстом), математические модели (описание при помощи математического аппарата), информационные модели (знаковое или символьное описание информационных процессов). Особенностью компьютерного математического моделирования является перенесение математической модели в среду ЭВМ и переход от аналитических методов к численным методам.
На практике это означает дискретизацию непрерывных переменных и функций, а также замену всех бесконечно малых и бесконечно больших величин некоторыми конечными величинами. Такое представление позволяет описать и перенести любые математические модели в среду некоторого языка программирования или в среду готовой компьютерной программы для дальнейшей работы с ней. В экономических задачах информация представляется чаще всего в табличных данных, то есть уже дискретная. Обрабатывая ее статистическими и эконометрическими методами, получаем математическую модель. В силу больших массивов данных их обработка и анализ модели не возможны без компьютерных технологий.
Составление любой модели проходит несколько этапов. На первом этапе выполняется словесная постановка задачи. Здесь определяется объект модели, начальные условия и что должно получиться в результате. Ключевая фраза: «Я хочу, чтобы. ». Следующим этапом является формализация, где уясняются существенные свойства объекта и их взаимосвязь.
Так как различные свойства существенны в различной степени для данной модели, то часть из них отбрасывается как несущественные. В силу последнего замечания адекватность модели реальности будет в той или иной степени приближенной.
Дальнейший этап состоит в поиске математического описания модели или в выборе из нескольких возможных. Это самый сложный и ответственный момент в моделировании, так как в модели может присутствовать достаточно большое количество связей, частей, переменных и выбор неправильного математического описания для любой из них может привести к полной или частичной неработоспособности модели в целом. Для описания взаимодействий выбираются уже известные функциональные зависимости, то есть исследованные ранее, или табличные описания — статистическую зависимость.
Последний этап состоит в программировании, то есть в перенесении полученной математической модели в среду ЭВМ. На этом этапе выбирается конкретная среда работы, или среда языка программирования, или среда существующего приложения, или то и другое. Создается, собственно, модель в виде программы или пользовательского документа. Проводятся тестирования модели с целью выяснения работоспособности и степени адекватности полученной модели. По завершению создаются инструменты работы с моделью (интерфейс).
Приведенное выше разделение моделирования на этапы носит в известной степени условный характер, так как они могут пересекаться, дополнять друг друга.
В качестве примера математического моделирования экономической задачи рассмотрим процесс роста выпуска продукции. [1]. Целью нашего моделирования будет изучение этого процесса, его графическое представление и определение прогнозных значений в некоторый момент времени.
Первый этап. Создать в среде MS Excel таблицу и диаграмму, позволяющие по заданным начальным параметрам определить уровень выпуска продукции в определенный момент времени и увидеть график его изменения во времени.
Второй этап. Для создания модели необходимо знать цену продукции, количество продукции, реализованной на момент времени t, инвестиции в производство.
Для проведения тестирования модели возьмем Q0=100 единиц товара в момент времени t=1 месяц, и k=0,1. Шаг — 1 месяц. Тогда, полученная в MS Excel [2] таблица выглядит следующим образом:
Источник: science-education.ru