Использование МатАнализа в компьютерных играх
Во многих играх, особенно РПГ очень большое значения имеют «статы». Атака, защита, сопротивление, урон, пробивание брони, промахи и прочее влияют на наносимый противнику урон или вами от противника получаемый. Чаще всего игроки предпочитают придерживаться тактики – «чем больше всего и сразу, тем лучше». Такой подход скорее вызван не продуманной стратегией развития персонажа, а отсутствием детального анализа игры, лени, или же недостатком информации о конкретном характере(конкретной расчётной формулы) влияния «статов» на те или иные показатели. Более того, очень часто, по задумке создателей игры, бывает невозможно увеличивать все характеристики одновременно, и поэтому правильно выбрать «что и куда «вкачивать» становится особенно важно.
Далее речь пойдет о способе, который позволит в ряде случаев получить явную формулу зависимости одних параметров от других (например силы заклинаний от интеллекта, или процент снижения получаемого урона от величины защиты). Данный метод применим там, где у нас есть возможность менять один параметр и наблюдать при этом изменения, от него зависящего, второго. Более того, этот метод применим и в том случае, когда среднее значение второго параметра строго зависит от первого, однако сам второй параметр является случайной величиной.
Что такое математический анализ?
Метод будет описываться на примере вычислении силы заклинаний питомцев от интеллекта, и процент снижения получаемого урона игроком от суммарной величины защиты в игре ArcheAge. Собственно основа метода это «Метод наименьших квадратов», который очень широко известен и очень часто используется в разных областях. Для вычислений будет использоваться Wolfram Mathematica (любая версия). Собственно пошаговое описание того, что нужно делать для получения интересуемого закона и является основной ценностью данной статьи. Те, кто знаком с МНК и Wolfram Mathematica, могут перейти непосредственно к примерам.
Метод наименьших квадратов (МНК)
Метод МНК очень подробно описан в литературе, я лишь в общих словах опишу суть. Пусть мы знаем общий вид зависимости одной величины от другой. Откуда можно узнать общий вид, я объясню позже. На данный момент для примера возьмём зависимость вида y=а*x^2 +b*x +c. Где y это одна величина, а x это другая. При этом a, b, c это некоторые параметры.
И что бы полностью опередить зависимость одной величины от другой, нужно определить именно эти параметры, ведь сам вид зависимости предполагается известным.
В самом простом случае можно узнать значение одной величины при каком-то конкретном значении другой величины из наблюдений, экспериментов или каких-то других источников. Таких пар нужно три, чтобы составить полную систему уравнений и решить её относительно трёх неизвестных параметров a,b,c. Более того, в ряде случаев этого бывает достаточно и в играх.
Всё усложняется, когда к функции зависимости добавлен ещё один член – а именно некоторая случайная величина. y=а*x^2 +b*x +c +Случайная_Величина. Она может быть введена разработчиками игры специально, как например разброс при уроне, но может иметь и иную причину. Дело в том, что точное значение некоторой функции может иметь в своей записи количество цифр большее, чем размер поля вывода в меню игры. В таком случае выводится округленное значение, и нельзя сказать точное значение больше или меньше чем то, что мы можем прочитать в поле интерфейса игры. Таким образом, можно сказать что округление нам добавляет некоторую случайную величину (она может быть и отрицательной и положительно, но в среднем она ноль).
Сдача мат анализа
Когда к «точной» функции зависимости y=а*x^2 +b*x +c добавляется случайная величина, то реально наблюдаемые, измеренные значения y не будут лежать на кривой а*x^2 +b*x +c какие бы ни были параметры. При ни слишком большой дисперсии (среднем значении разброса) случайно величины, реально наблюдаемые значения, отмеченные на координатной плоскости будут лежать довольно «близко к кривой а*x^2 +b*x, если мы даже знаем параметры a b и с. Часть точек даже может попасть на эту кривую, т.к. вполне возможно что случайная величина в какой-то момент просто приняла значение ноль. Но как в таком случае нам найти параметры нашей функции если даже точки, которые мы знаем, на ней не лежат? МНК заключается в том, чтобы так подобрать параметры, чтобы расстояние от точек до кривой было минимальным! Это главная суть МНК.
Тут стоит уточнить, что под расстоянием от точки до кривой подразумевается не расстояние до ближайшей точки кривой, а разница между значением точки (точка это пара переменная величина — наблюдаемое значение функции) и «точным»значением функции при том же значении переменной что и у точки. Вообще говоря в идеальном случае эта разница равна конкретному значению той самой Случайной_Величины в данной точке.
Уточнить стоит так же то, что нужно, чтобы сумма именно всех разностей между наблюдаемыми значениями и «точными» значениями была минимально. К сожалению, часто возникает соблазн выкинуть наиболее «неудобные», сильно отстающие от предполагаемой «точной» кривой точки, чтобы всё остальное смотрелось лучше. Этого делать нельзя, если конечно вы абсолютно не уверены что измерение было проведено ошибочно. И ещё один важный момент – расстояние в данном случае измеряется как строго положительная величина. Не важно, выше наблюдаемая точка, чем нужно или ниже – главное это как далеко.
Общий вид зависимости, как было сказано ранее y=а*x^2 +b*x +c +Случайная_Величина. Причём, из наблюдений мы знаем наблюдаемые значение пар обеих величин x,y. Пар мы можем измерить столько сколько захотим, и желательно чем больше, тем лучше! (почем это так, читайте в литературе).
Чтобы найти разницу между наблюдаемым и «точным» значением нужно вычесть измеренные значение величин y_измер и а*x_измер ^2 +b*x_измер+c. То есть мы считаем, что переменная у нас известна точно, и что при точных параметрах a b c а*x_измер ^2 +b*x_измер+c это как бы «точное» значение нашей функции. От полученной разности нужно взять модуль, чтобы получить как уже говорилось абсолютное значение.( Стоит отметить, что на самом же деле «точная» означает такую кривую, которая наиболее близко расположена ко всем точкам. Реально_Точное значение мы не можем вычислить никак. Но за неимением Реально_Точного остаётся довольствоваться тем, что можно посчитать.
К такому повороту событий если вы ещё не привыкли, то стоит привыкнуть. Когда нет идеала – используем лучшее из того что есть.) Но с модулем неудобно работать, и проще вместо модуля возвести полученную разность в квадрат. И просуммировать все квадраты разностей. Полученная сумма будет одной очень длинной функцией со множеством слагаемых, но всего от трёх переменных.
Остаётся лишь найти такие значения a b c при которых эта функция будет минимальной. Что равносильно нахождению экстремумов функции от нескольких переменных. Что в свою очередь (на первый) взгляд является тривиальной задачей мат анализа. Это и есть метод наименьших квадратов.
Кажущаяся простота метода играет довольно злую шутку, когда нужно написать алгоритм для вычислений. Это действительно довольно сложная задача, с массой подводных камней. Однако существуют уже реализованные алгоритмы, которыми мы и воспользуемся, в силу того, что наша цель именно использование метода МНК, а не написание очередного алгоритма для его реализации.
Wolfram Mathematica
Если вы никогда не работали с программами типа Mathematica MATLAB и Maple, то самое время начать. Если совсем очень просто, (так чтобы вы не пугались их осваивать) то эти программы нужны для того, чтобы решать системы дифференциальных уравнений символьно, или интегрировать символьно, или нарисовать график, причём всё это делается «вежливой просьбой» в одну строчку.
Вы только подумайте, вы пишете уравнение, в символьном виде (НЕ ЧИСЛОВОМ! Всё буквами, переменными, параметрами) и получаете такой же ответ – в общем символьном виде. Нахождение параметров методом АНК они тоже умеют. (…и не только им, но это уже детали). Советую попробовать поиграться с Wolfram Mathematica.
Может кому станет интересенее если вы узнаете тот факт, что из Mathematica есть доступ к базам данных соцсетей, например вконтакте. (Понятно что только открытых данных, но всё же) Вы можете сами проводить какие-то исследования, используя данные реальных людей. Их вкусы, профессии, интересы, частоту постов, и всё что захотите касательно социологии и поведения людей. Статей как работать с Mathematica очень много, но что особенно приятно, это колоссальное количество примеров во встроенном хелпе – буквально на все случаи жизни. Это очень упрощает осваивание Mathematica (про MATLAB я так лестно не буду отзываться: у него тоже, конечно, есть плюсы, но всё же мой выбор за Mathematica).
Пара слов о тех функция которые будут применятся ниже. Для нахождения параметров функции известного типа, при наличии набора наблюдаемых (измеренных) данных (к которым добавлена некоторая случайная величина), используется функция FindFit. Для отображения массива точек используется функция ListPlot. Для построения графика используется просто Plot.
Массивы обычно заключены в фигурные скобки <>, доступ к элементу массива производится через двойные квадратные скобки [[]]. Так же для создания массива можно использовать различные функции, например Table. Для отображения графика и массива точек на одном рисунке используется функция Show[<>] от массива из двух элементов (или более) каждый из которых может являться любой функцией для графического отображения данных.
Примеры
В большинстве случаев, в играх не используются слишком сложные функции для зависимостей одних параметров от других. Чаще всего используются линейные функции ax+b, либо отношение вида (ax+b)/(cx+d). Нет чёткого правила для поиска функций. Разработчик может при желании сделать очень сложную и запутанную функцию, которую угадать почти невозможно. Однако такие случаи крайне редки.
Отношение вида (ax+b)/(cx+d) часто используется там, где вычисляется значение, которое должно быть ограничено сверху, например снижение получаемого урона от значения защиты. Действительно, нет смысла вводить такое понятие как снижение урона больше чем 100%. В подобных случаях, когда есть величины ограниченных сверху, лучше всего начать пробовать именно с функции вида y= (ax+b)/(cx+d).
Попробуем найти зависимость процента снижения получаемого урона от величины защиты. Для этого нам нужно получить пары чисел (защита, процент). Делается это довольно просто. С персонажа снимаются все предметы. И после чего по очереди, в разном количестве, в разных комбинациях надеваются обратно. Таким образом, мы варьируем значение защиты, и смотрим, как изменяется процент.
Полученные результаты мы записываем в массив, вот в таком виде.
После этого нам для удобства дальнейшего графического представления точек, будет полезно найти минимальное и максимальное значение защиты. А так же отсортируем наши данные. Transpose из массива двух мерных массивов делает массив из двух одномерных массивов, чтобы потом вычислить минимальное и максимальное значение защиты.
Def=Sort[OurDef,#1[[1]] MaxDef=Last[Transpose[Def][[1]]];
MinDef=First[Transpose[Def][[1]]];
После чего мы задаём общий вид нашей функции, и создаем массив всех параметров, которые нужно будет найти.
После чего используем FindFit для поиска параметров функции определённого вида, используя полученные экспериментальным путём данные.
После чего показываем вид функции с найденными параметрами ( для этого используется «/.» )
В результате мы получаем: (-1.1499 + 7.32728 x)/(388.234 + 0.0732995 x)
Надо сказать, вид очень не красивый. И скажу сразу, очень редко используются не красивые коэффициенты, в силу того, что разработчикам самим гораздо проще работать с какими-то компактными, наглядными коэффициентами. Но полученный нами результат это дробь, которую мы можем сократить, что-то вынести за скобочки. Будем приводить к более красивому виду.
Если приглядется, то видно что коэффициенты перед х в числителе и знаменателе совпадают. Разделим на коэффициент при х в числителе обе части дроби.
(-0.156933+ x)/( 52.9848_+0.0100036 x)
Как мы помним переменная x означает величину защиты в единицах. Характерные значения для x порядка тысяч. Поэтому числовой константой в числителе можно пренебречь, что означает что общий вид функции на самом деле несколько иной, чем мы предполагали, а именно без константы в числителе. Что касается знаменателя, то множетель перед х очень похож на 0.01.
Слагаемое же в знаменателе очень похоже на 53.00. Сделав все эти допущения, а также умножив знаменатель на 100, получаем, что процент снижения получаемого урона равен 100*x/(5300+x), где — х это суммарное количество защиты.
Для проверки насколько «красивая» формула соответствует действительности, найдем разности между экспериментальными точками и значениями нашей функции.
Макимальное значение разности 0.00493997, что меньше половины последней значимой(отображаемой) цифры в значении процентов. Что вполне удовлетворительно.
Результат можно отобразить на графике.
Полный код для Mathematica:
OurDefSource = , , , , , , , , , , , , , >; Def = Sort[OurDefSource, #1[[1]] < #2[[1]] MaxDef = Last[Transpose[Def][[1]]]; MinDef = First[Transpose[Def][[1]]]; Fdef[x_] := (a*x + b)/(c*x + d); CoefsFdef = ; CoefsFdefFit = FindFit[Def, Fdef[x], CoefsFdef, x] Fdef[x] /. CoefsFdefFit OurDiff = Fgood[x_] := 100*x/(5300 + x); OurDiff = Table[Fgood[Def[[i]][[1]]] — Def[[i]][[2]], ] Max[OurDiff] Show[ ], Plot[Fgood[x], , PlotStyle -> ]>]
Подобный подход так же успешно работает при вычислении формулы расчёт урона заклинания Ядовитое дыхание пета Обращенная ведьма от бонуса инты со шмота. В этом примере общий вид функции будет несколько иной. Если предположить, что формула для пета будет аналогично формуле для персонажа, то инта сначала преобразуется в силу заклинаний, потом к этой силе добавляется что-то ещё (со шмота или бафов), после чего полученная сила заклинаний преобразуется по какой-то формуле в урон от конкретного заклинания. Причем часто урон от заклинаний имеет константную часть, которая не зависит от силы заклинаний. Таким образом, формула предположительно должна иметь вид
где a51 это константа в расчёте конкретного спела; b51 это множитель в формуле спела; c51 это коэффициент пропорциональности силы заклинаний и инты; x это инта а y это бонусный прирост к силе заклинаний со шмота. FindFit способна работать и для функции от нескольких переменных. В результате мы получаем:
Урон заклинания Ядовитое дыхание=1669+4.8*(1.25* Инта+БонусСилаЗакл);
Стоит заметить, что в отличии от персонажа, коэффициент пропорциональности силы заклинаний и инты равен не 0.2 а 1.25, что означает что сила заклинаний от спелов у петов растёт в почти в 6 раз быстрее.
«ураган лесовика» 654+1.92*(1.25* x+y);
«стрела лесовика” 980+2.88*(1.25* x+y);
Выводы
Таким образом, используя довольно простую методику можно получать информацию о законах и принципах игры. Попутно, как было показано, мы узнали не только зависимость одного параметра от другого, но ещё и заметили то, чего изначально и не искали даже, как например коэффициент с51. Теперь, зная точную формулу для расчёта, можно анализировать и моделировать, какие параметры и как улучшать. Таким образом, стратегия развития персонажа становится более осмысленной.
Данный метод никак не относится ни к взлому кода, ни к чему-либо ещё противозаконному. Но согласитесь, этот метод позволяет вам увидеть то, что явно не показано для всех остальных.
Заключение
Матан помогает даже в играх. Надеюсь описанный пример использования МНК в играх, увеличит ваш интерес к матану.
Источник: habr.com
Математика для чайников. Глава 9. Основы матанализа
Многих матанализ пугает. Но на самом деле, если вы понимаете, что такое математическая абстракция, то матанализа не стоит бояться. Математический анализ – это просто набор абстракций чуть более высоко уровня, чем алгебра. Ну а если понятие математической абстракции вам незнакомо, можете прочесть предыдущие урок, начиная с Математика для чайников. Глава 1. Что такое математическая абстракция .
Итак, прежде всего, давайте ответим на вопрос: А что же такое, математический анализ? А узком смысле слова математический анализ – это анализ бесконечно малых величин. В такой анализ входят, как правило, дифференциальные и интегральные исчисления. В более широком смысле, кроме дифференциалов и интегралов, в математический анализ входит:
· Теория функций. Это о том, что такое функция вообще (точное определение), какие бывают функции, что вообще можно делать с функциями, различные свойства функций, способы приближенного вычисления функций и многое другое.
· Теория комплексной переменной. По сути, это та же теория функций, но связанная с комплексными числами. Комплексное число – это число, состоящее из «нормального» числа и мнимой единицы, умноженной на некий коэффициент. А мнимая единица – это корень из минус единицы, которого как бы не существует, но он на самом деле существует.
· Функциональный анализ. Это, по сути теория функций, но скрещенная с топологией. То есть туда добавлены такие понятия, как «пространство». Данный раздел математики изучает поведение и взаимоотношения функций в различных пространствах, плюс всякие линейные операторы и прочее тому подобное.
· Вариационное исчисление. Объект изучения этого раздела так называемые «вариации функционалов». Что это такое? Это обобщенное понятие дифференциала функции. Дифференциал – это, по сути, бесконечно малая часть приращения функции. С ним тесно связано понятие производной – скорости изменения функции. Для чего все это нужно?
Чтобы найти экстремумы функции – ее минимумы и максимумы. А для чего их искать? Это нужно в задачах оптимизации. Например, в задачах искусственного интеллекта и машинного обучения необходимо найти минимум ошибки.
· Гармоничный анализ. Здесь задача сводиться к исследованию гармонических функций (синусоида, например). Это про ряды Фурье и прочее тому подобное.
· Дифференциальные и интегральные уравнения. Дифференциальное уравнение – это уравнение, в котором фигурирует производная или дифференциал. Их решение сводиться к тому, чтобы преобразовать уравнения так, чтобы его можно было проинтегрировать. Ну а дальше решаем интеграл и получаем ответ.
А интеграл – это сумма бесконечно малых кусочков функции, если говорить простыми словами, ну или площадь фигуры которую «вырезает» график функции. Нетрудно догадаться, что интегральные уравнения – это уравнения, где есть интеграл. А вот как решать такие уравнения – целая наука. Существует много методик, например, преобразование Лапласса.
· Теория динамических систем. Это наука о том, как изменяются во времени различные системы с взаимосвязанными элементами, особенно механические системы. Как правило, для решения таких задач как раз и используют дифференциальные уравнения.
· Эргодическая теория. Здесь можно заметить, что динамические системы с определенной вероятностью повторяют свои состояния. Такое их свойство называют эргодичностью.
· Глобальный анализ. А вот это очень абстрактная абстракция. Гораздо абстрактнее, чем дифференциальные и интегральные уравнения, ибо в глобальном анализе они представлены на многообразиях пространств и векторных расстояниях.
· Нестандартный анализ. Это альтернативная теория, в которой бесконечно малые величины – это ни какие не переменные, а особый вид чисел. Считается, что нестандартный анализ способен изучать свойства актуально бесконечных объектов, предлагая новые методы моделирования, недоступные стандартной математике.
Ну, а теперь вернемся к основам математического анализа. Начнем с функций . Классическое определение гласит, что функция – это соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу второго множества соответствует один и только одни элемент из второго множества. Что такое множество, вы может узнать здесь: Математика для чайников.
Глава 7. Множества . Обычно эти множества – это множества действительных чисел (но не всегда). Функция может быть и комплексная, и векторная, и даже матричная. А вообще соответствие (функцию) можно задать на любых множествах, даже самых экзотических.
Но мы с вами поговорим о числовых функциях. В данном случае это будет просто соответствие одних чисел (аргументов) другим числам (значениям). Множество аргументов называется областью определения функции, а множество значению – областью значений функции. Функцию можно задать в виде таблицы, в виде графика, в виде формулы или в виде какого-то правила. Обычно математический анализ имеет дело с функцией, заданной в виде формулы.
Другой объект, немного похожий на функции, и который тоже может встретится в матанализе — это числовая последовательность . Классическое определение последовательности такое: последовательность — это пронумерованный набор каких-либо объектов, среди которых допускаются повторения, причём порядок объектов имеет значение. Нумерация чаще всего происходит натуральными числами. Соответственно, в случае числовой последовательности такими объектами являться числа. Есть еще строго определение. Оно звучит так: пусть задано некоторое множество X элементов произвольной природы.
Источник: dzen.ru
Примерная программа дисциплины Мат. Анализ 1 курс
Документ из архива «Примерная программа дисциплины Мат. Анализ 1 курс», который расположен в категории » «. Всё это находится в предмете «математический анализ» из раздела «», которые можно найти в файловом архиве МГУ им. Ломоносова. Не смотря на прямую связь этого архива с МГУ им. Ломоносова, его также можно найти и в других разделах. .
Онлайн просмотр документа «Примерная программа дисциплины Мат. Анализ 1 курс»
Текст из документа «Примерная программа дисциплины Мат. Анализ 1 курс»
В результате изучения дисциплины студент должен:
Знать и уметь применять на практике основные методы математического анализа
уметь понимать и применять на практике компьютерные технологии для решения различных задач математического анализа,
владеть навыками решения практических задач математического анализа
Обязательный курс для студентов 1 курса,
читается в 1 и 2 семестрах (Цикл ЕМНД),
Лекции – 102 часа, семинары – 102 часа,
Зачёт и экзамен в 1 семестре, зачёт и экзамен во 2 семестре,
За курс отвечает кафедра общей математики,
Авторы программы: академик Ильин В.А., доцент Фоменко Т.Н.,
Лектор 2008/09 учеб. года: доцент Фоменко Т.Н.
3. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ.
Перечень разделов курса (в том числе перечень тем семинарских занятий, при наличии описание практикума, коллоквиума).
3.1 ЛЕКЦИИ, I СЕМЕСТР
1. Вещественные числа
Введение. Предмет математического анализа. Естествознание как источник основных понятий математического анализа.
Теория вещественных чисел. Элементы теории множеств. Числовые множества, натуральные, целые, рациональные числа. Необходимость расширения множества рациональных чисел. Вещественное число как бесконечная десятичная дробь. Понятие о числовой оси. Сравнение вещественных чисел. Существование точных граней у ограниченных числовых множеств. Арифметика вещественных чисел.
Понятие счётных и несчётных бесконечных множеств, их неэквивалентность. Несчётность множества вещественных чисел. Понятие о полноте числового множества относительно заданных правил и свойств. Полнота множества вещественных чисел.
2. Предел числовой последовательности
Последовательности вещественных чисел, понятие предела. Понятие о числовой последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. Предел последовательности. Свойства сходящихся числовых последовательностей. Критерий Коши сходимости последовательности.
Сходимость монотонных последовательностей. Число “e” как предел монотонной последовательности.
Частичные пределы последовательности. Предельные точки (частичные пределы) последовательности и предельные точки числового множества. Теорема Больцано–Вейерштрасса о существовании частичного предела у ограниченной последовательности. Теорема о существовании верхнего и нижнего пределов у числовой последовательности.
3. Предел и непрерывность функции одной переменной
Предел функции одной вещественной переменной. Отображения множеств, в том числе взаимно-однозначные. Понятие о функции как однозначном отображении числовых множеств. Способы задания функций. Предел (предельное значение) функции в точке – определения по Коши и по Гейне и их эквивалентность.
Односторонние пределы. Расширенная числовая ось. Пределы функций в бесконечно удалённых точках и бесконечные пределы. Свойства функций, имеющих (конечные) пределы. Критерий Коши существования предела функции. Ограниченные, неограниченные, бесконечно малые, бесконечно большие функции.
Асимптотическое сравнение функций. Символы о-малое, О-большое, О*(О-большое со звёздочкой).
Непрерывность функции в точке и на множестве. Понятие о непрерывности функции в точке. Точки разрыва функции и их классификация. Суперпозиция функций (сложная функция). Непрерывность суперпозиции непрерывных функций.
Локальные свойства непрерывных функций. Непрерывность функции на множестве. Свойства функций, непрерывных на замкнутом отрезке. 2 теоремы Вейерштрасса. Понятие о равномерной непрерывности функции на множестве. Теорема Кантора о равномерной непрерывности функции на замкнутом отрезке.
Монотонные функции. Понятие об обратной функции. Существование односторонних пределов у монотонных функций. Условия существования и непрерывности обратной функции. Первый и второй замечательные пределы.
Основные свойства простейших элементарных функций и их непрерывность.
4. Дифференцирование функций одной переменной
Производные и дифференциалы первого и высших порядков. Производная функции в точке, её геометрический и физический смысл. Понятие дифференцируемости функции в точке и существование производной. Первый дифференциал функции. Связь дифференцируемости и непрерывности функции в точке.
Производные и дифференциалы суммы, произведения, частного двух функций. Производная сложной функции и инвариантность формы записи первого дифференциала. Производная обратной функции и функции, заданной параметрически. Производные простейших элементарных функций.
Формула Лейбница. Примеры производных высших порядков простейших элементарных функций.
Применение производных для исследования свойств функций. Возрастание и убывание функции в точке. Локальный экстремум функции. Необходимое условие существования локального экстремума дифференцируемой функции. Критерий нестрогой и достаточное условие строгой монотонности дифференцируемой функции.
Теоремы Ролля, Лагранжа, Коши. Следствия из теоремы Лагранжа. Правила Лопиталя раскрытия неопределённостей. Формула Тейлора. Выражение остаточного члена в формуле Тейлора в общей форме Шлёмильха-Роша, а также в формах Лагранжа, Коши и Пеано.
Формула Маклорена. Примеры разложения по формуле Тейлора-Маклорена элементарных функций.
5. Интегрирование функций одной переменной
Понятие первообразной функции. Связь операций дифференцирования и интегрирования. Основные методы вычисления неопределённого интеграла: метод подстановки (замена переменной), интегрирование по частям. Интегрирование рациональной функции путём разложения её в сумму простейших дробей.
Интегрирование некоторых иррациональных выражений – подстановки Эйлера, тригонометрические и другие подстановки. Интегрирование тригонометрических функций – универсальная тригонометрическая подстановка, другие подстановки.
6. Исследование функции и построение её графика
Достаточные условия существования локального экстремума функции. Краевые экстремумы. Общая схема отыскания наибольшего (наименьшего) значения функции на замкнутом отрезке. Направление выпуклости графика функции. Достаточные условия выпуклости вверх (вниз) графика функции. Понятие точки перегиба графика функции.
Достаточные условия существования перегиба графика функции. Вертикальные и наклонные асимптоты графика функции, их отыскание. Общая схема исследования функции и построения её графика.
3.2 ЛЕКЦИИ, II СЕМЕСТР
7. Определённый интеграл Римана
Определённый (собственный) интеграл Римана. Разбиение отрезка. Размеченное разбиение. Интегральная сумма функции по данному размеченному разбиению. Определённый интеграл как предел интегральных сумм. Суммы Дарбу и их свойства.
Интегралы Дарбу. Критерии интегрируемости функции на отрезке в терминах сумм Дарбу и в терминах интегралов Дарбу. Основные классы интегрируемых функций – непрерывные, монотонные, кусочно-непрерывные функции. Свойства определённых интегралов. Формула Ньютона-Лейбница. Существование первообразной у непрерывной функции.
Первая и вторая теоремы о среднем значении определённого интеграла. Замена переменной и интегрирование по частям в определённом интеграле.
Несобственный интеграл Римана. Понятие о несобственных интегралах первого и второго рода. Критерий Коши сходимости несобственного интеграла. Замена переменной и интегрирование по частям несобственного интеграла. Понятие об абсолютной и условной сходимости несобственного интеграла первого рода.
Признаки сходимости несобственных интегралов первого рода: признаки сравнения, признак Абеля-Дирихле. Связь несобственных интегралов первого и второго рода.
8. Приложения и приближённые вычисления интеграла Римана
Геометрические приложения определённого интеграла. Способы задания кривых на плоскости и в пространстве. Простые и параметризуемые кривые. Длина дуги спрямляемой кривой. Квадрируемая плоская фигура и её площадь.
Кубируемое пространственное тело и его объём. Вычисление площадей плоских фигур, объёмов тел вращения, площадей поверхностей вращения.
Приближённые методы вычисления определённых интегралов и отыскания корней уравнений. Методы отыскания корней уравнений: метод последовательных приближений, метод хорд, метод касательных (Ньютона). Приближённое вычисление определённых интегралов Римана: метод прямоугольников, метод трапеций, метод Симпсона. Оценки погрешностей.
9. Предел последовательности в E n и предел функции нескольких переменных
Предел последовательности в n-мерном евклидовом пространстве. Евклидово пространство , скалярное произведение в нём. Норма элемента и её свойства. Метрика в пространстве . Сходящиеся последовательности в и их свойства. Критерий Коши сходимости последовательности в . Шар, сфера в , окрестности точки, ограниченные и неограниченные, открытые и замкнутые множества.
Кривая в . Понятие области в . Предельные точки множества в . Частичные пределы (предельные точки) последовательностей. Теорема Больцано-Вейерштрасса для последовательностей в .
Предел и непрерывность функции нескольких переменных. Функция нескольких переменных, её область определения, область значений. Понятия предела (предельного значения) функции нескольких переменных по Коши и по Гейне и их эквивалентность. Критерий Коши существования предела функции нескольких переменных. Непрерывность функции нескольких переменных в точке.
Локальные свойства непрерывных функций. Понятие сложной функции нескольких переменных, условия её непрерывности. Непрерывность функции нескольких переменных в замкнутой области. 2 теоремы Вейерштрасса. Понятие равномерной непрерывности функции на множестве.
Теорема Кантора для функции нескольких переменных.
Источник: studizba.com
Матан что это за программа

На этом свойстве производной основан самый популярный метод машинного обучения – градиентный спуск (и вообще практически все методы машинного обучения). Градиент функции нескольких переменных – это вектор ее частных производных по каждой из этих переменных:
∇ L ( w 1 , w 2 , . . . w n ) = [ ∂ L ∂ w 1 , ∂ L ∂ w 2 , . . . ∂ L ∂ w n ]
В данном случае L – это функция потерь (Loss) нашей модели машинного обучения, а w1. wn – внутренние параметры модели, которые должны изменяться в процессе ее обучения (веса). Функция потерь измеряет «качество» модели, она может быть очень разной в зависимости от задачи. Например, для модели, предсказывающей значение одной переменной, это может быть квадрат разности между истинным значением этой переменной и предсказанным.
Нам нужно найти глобальный минимум функции потерь в пространстве весов – то есть, такие значения весов, при которых модель будет оптимальной. Метод градиентного спуска на каждом шагу рассчитывает градиент в данной точке n-мерного пространства весов и переходит в следующую точку, двигаясь по направлению вектора градиента.
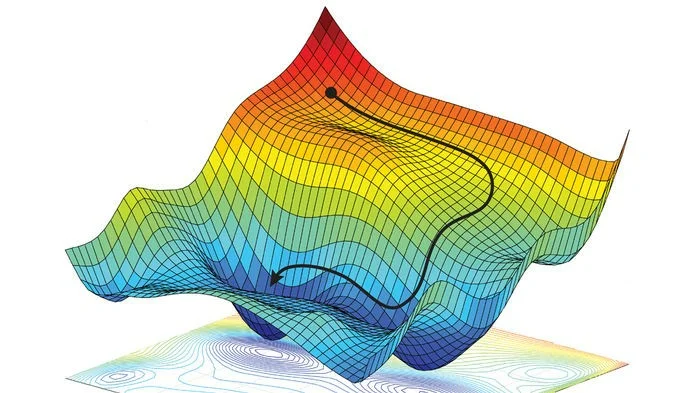
Идея метода градиентного спуска очень проста: «если идти все время вниз, то когда-нибудь достигнешь дна». Чтобы узнать, в каком направлении находится «низ», мы и считаем вектор градиента.
Цепное правило и back-propagation
Изучая математический анализ, вы познакомитесь с цепным правилом вычисления производной – это правило вычисления производной сложной функции:
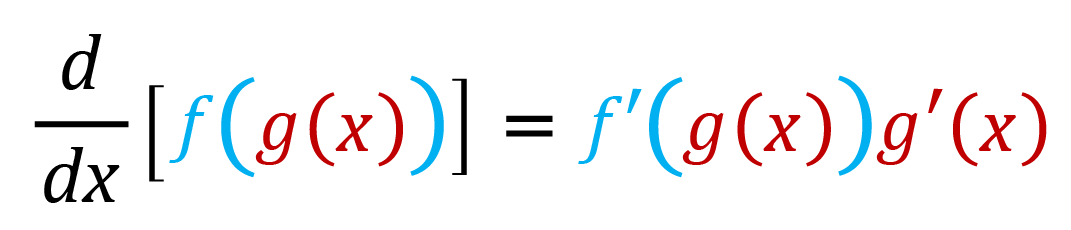
Поскольку все нейронные сети состоят из нескольких слоев, и входом каждого слоя сети, кроме первого, является выход предыдущего слоя, результат работы сети (прямого прохода) – это именно сложная функция, в которой функция активации нейронов каждого слоя выполняется над результатами функции активации предыдущего.
Для обучения нейронной сети нам нужно рассчитать градиент ее функции потерь, то есть набор производных этой функции по всем весам сети. Как видно на следующем рисунке, цепное правило позволяет представить производную по каждому весу в виде произведения более простых элементов (производных функции потерь и функций активации нейронов по их параметрам), которые мы уже можем рассчитать.
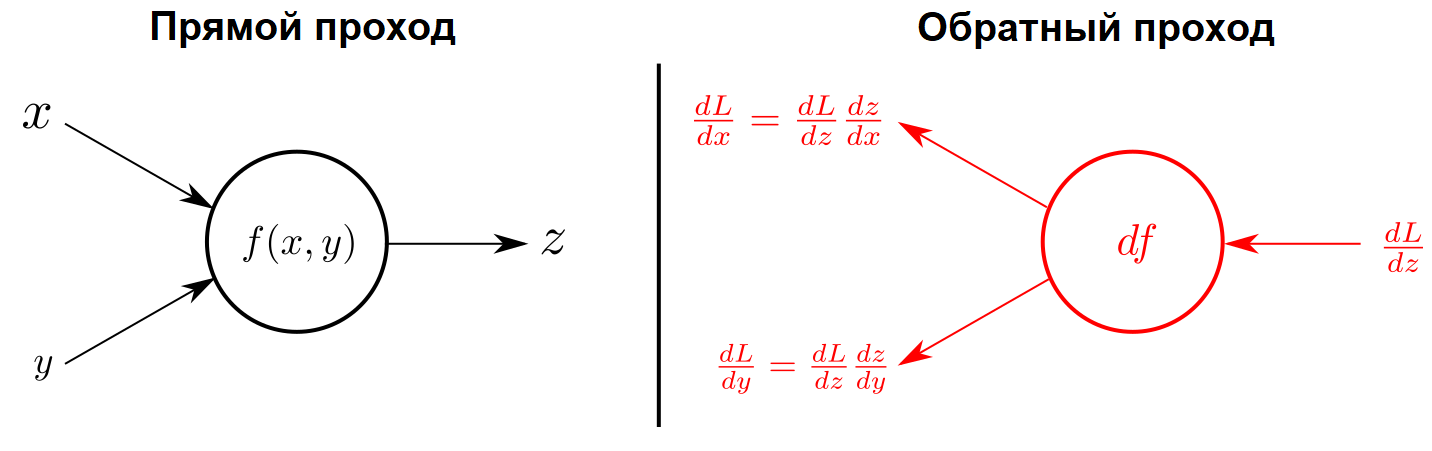
Такой метод расчета градиента называется обратным распространением ошибки, или просто обратным распространением (back-propagation). Именно этот метод дал старт широкому распространению всех видов нейронных сетей, которые изменили мир. История искусственных нейронных сетей началась еще в 1960-х, но лишь недавно появились вычислительные мощности, позволяющие реализовать обратное распространение.
Плотность распределения вероятности
Одно из самых очевидных применений интегралов в машинном обучении – это интегрирование функции плотности распределения вероятности, занимающей центральное место в статистике. Вероятность того, что случайная величина находится в интервале между alpha и beta, равна определенному интегралу по функции плотности вероятности с этими пределами.
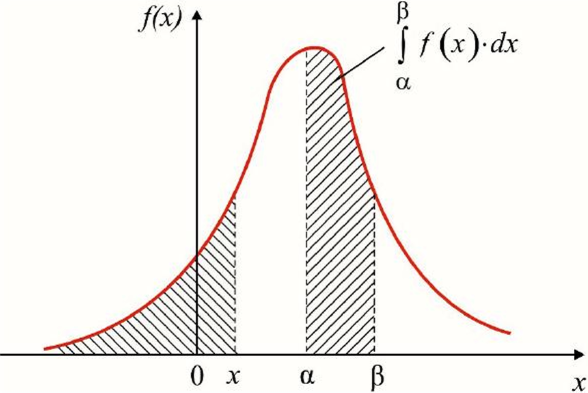
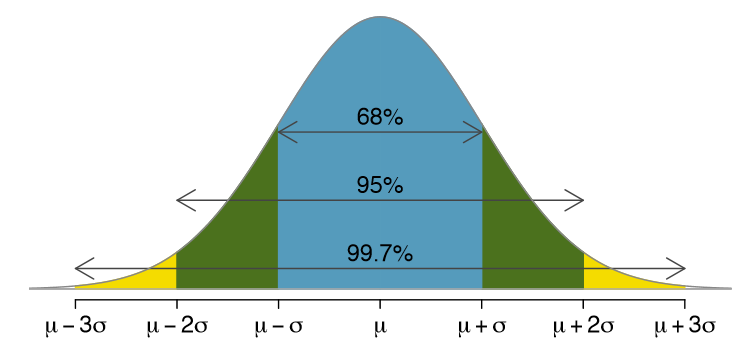
Именно из этой формулы следует знаменитое правило трех сигм – эмпирическое правило, согласно которому 68% значений нормально распределенной случайной величины находятся в пределах одного стандартного отклонения от среднего значения, 95% значений – в пределах двух отклонений, и 99.7% (почти все) – в пределах трех отклонений.
Заключение
Мы привели лишь несколько самых очевидных примеров применения математического анализа в машинном обучении. Менее очевидные встречаются буквально везде! Например, при выборе функции активации слоя нейронов надо учитывать опасность взрывных/исчезающих градиентов, то есть уметь анализировать поведение этой функции.
«Прикладное машинное обучение», в основном, это конструирование признаков.
Конструирование признаков (feature engineering) – это искусство создания нужных признаков на основе исследовательского анализа данных (exploratory data analysis, EDA). Например, анализ данных может показать квадратичную зависимость целевой переменной от некоторого признака – то есть, можно ввести признак, равный квадратному корню исходного, от которого целевая переменная будет зависеть линейно. Чтобы хотя бы заметить эту квадратичную зависимость, а тем более доказать ее, нужно очень хорошо знать математический анализ.
Поэтому самым правильным ответом на вопрос «для чего в машинном обучении нужен математический анализ», будет «для всего». Нет ни одной области машинного обучения (и науки о данных вообще), в которой он бы не применялся.
В следующих статьях мы рассмотрим самые популярные приложения линейной алгебры и теории вероятностей в машинном обучении и науке о данных.
Если вы хотите наработать необходимую для изучения Data Science математическую базу, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.
Источник: proglib.io