Конечный автомат как автоматическое устройство, перерабатывающее информацию, ограничено в своих возможностях. Например, мы уже знаем, что с помощью КА невозможно решить проблему умножения двух чисел, с помощью КА невозможно распознать язык . Основным ограничением конечного автомата является конечность его памяти. В то же время при выполнении алгоритма в интуитивном смысле мы можем пользоваться потенциально неограниченной памятью, запоминая в процессе выполнения алгоритма по мере необходимости нужную информацию. Именно поэтому конечный автомат не может быть использован как модель устройства, выполняющего произвольные алгоритмы. Можно предположить, что если к модели КА добавить возможность запоминания произвольно больших объемов информации, то его возможности по выполнению алгоритмов расширятся.

Рис.5.1. Сравнение определений машины Тьюринга и конечного автомата
Алан Тьюринг в 1936г. предложил формальную модель вычислителя, которая является результатом простого добавления потенциально бесконечной памяти к конечному автомату.
Конструирование машины Тьюринга
Конечный автомат можно представить себе как устройство с конечным числом внутренних состояний, работающее с двумя лентами: входной и выходной (рис.5.1). Конечный автомат работает по тактам. На каждом такте он читает с помощью некоторой входной головки символ из обозреваемой ячейки входной ленты, изменяет свое состояние и печатает некоторый символ выходного алфавита в обозреваемую ячейку выходной ленты, после чего две его головки чтения и записи перемещаются на одну позицию вправо. Описание функционирования конечного автомата можно считать его программой: в ней просто перечислено конечное число четверок (команд) <(s,a)(p,y)>,гдеs — текущее состояние,a — очередной входной сигнал,р- следующее состояние иу- очередной выходной сигнал. Программа КА — это просто перечисление аргументов и соответствующих результатов частично-определенной функции переходов и выходов автомата:SXSY.
В своем вычислительном устройстве Тьюринг просто смоделировал доведенный до самых элементарных операций процесс выполнения произвольного алгоритма человеком. Человек имеет конечную память, и в этом смысле его можно представить системой с конечным числом состояний. Исходная информация к алгоритму обычно представляется в виде цепочки символов.
Выполняя алгоритм, человек-вычислитель использует дополнительную память (листы бумаги) для записи информации, причем эта запись производится им символ за символом. При вычислениях человек может возвращаться к ранее записанной информации, стирать некоторую информацию и т.д.
Таким образом, элементарными операциями при выполнении алгоритма можно считать запись или стирание символа и перенесение внимания с одного участка памяти на другой. Поэтому предложенная Тьюрингом формальная модель вычислителя — Машина Тьюринга (МТ) — отличается от конечного автомата только в двух аспектах: она имеет одну бесконечную рабочую ленту, с которой читает и куда пишет символы, и одну головку чтения-записи, которая может двигаться по рабочей ленте в любую сторону (рис.5.1). Такая свобода движения головки чтения-записи по сути означает возможность создавать и впоследствии анализировать промежуточную информацию. Как оказывается,такое простое расширение радикально увеличивает вычислительную мощность машин Тьюринга по сравнению с обычными конечными автоматами.
Машина Тьюринга в двух словах.
Машина Тьюринга работает по тактам. На каждом такте она читает символ из обозреваемой ячейки рабочей ленты, изменяет свое состояние в зависимости от своего внутреннего состояния и прочитанного символа и печатает символ в обозреваемую ячейку рабочей ленты, после чего ее головка чтения-записи перемещается на одну позицию влево, вправо или остается на месте. Описание функционирования МТ можно считать ее программой, в которой перечислено конечное число пятерок (команд) <(s,a)(p,y,D)>,гдеs, a, риу имеют тот же смысл, что и в конечном автомате, аD — направление перемещения головки по рабочей ленте, которое может быть одним из трех значений:L — влево,R — вправо и Н — оставаться на месте. Иными словами,программа МТ- это просто конечный список аргументов и соответствующих результатов ее частично-определенной функции переходов и выходов:SXSXГ.
Машина Тьюринга имеет один конечный рабочий алфавит X, в котором входные и выходные символы не различаются: выходной символ, напечатанный на ленте, машина может читать в последующих тактах. Для удобства обычно считают, чтоXсодержит пустой символ, находящийся во всех ячейках рабочей ленты слева и справа от конечной цепочки “значащих” символов в начале работы.
Пусть МТ находится в состоянииqи в обозреваемой ячейке ленты находится символх. Если в программе МТ нет команды для парыq,x>, то МТ останавливается. Если в программе МТ несколько команд для данной парыq,x>, то это — недетерминированная машина Тьюринга, в ней выполняется одна из нескольких возможных команд с левой частьюq,x>.
Очевидно, что в любой момент работы на ленте МТ находится только конечная цепочка “значащих” символов. После останова машины Тьюринга такая цепочка является результатом переработки входной цепочки. Таким образом, МТ являетсяавтоматом-преобразователемсимвольных цепочек. Машина Тьюринга также может бытьраспознавателеммножеств цепочек.
В МТ выделяются специальные заключительные состояниястоп или “!”, и если МТ, работающая как распознаватель, останавливается в одном из этих состояний при пустой входной ленте, то она распознает входную цепочку. Если в заключительном состоянии останавливается машина-преобразователь Тьюринга, то информация на рабочей ленте является результатом переработки входной информации.
Конфигурацией машины Тьюринга называется ее текущее состояние, текущее состояние рабочей ленты и место расположения головки. При работе МТ в каждом такте происходит смена конфигураций.
Пример 5.1. Построим МТ, распознающую язык. Представлять МТ будем подобно конечному автомату с помощью графа переходов, в котором каждой команде<(q,x)(p,y,D)>соответствует ребро, направленное из вершины, помеченной состояниемqв вершину, помеченную состояниемр. Само ребро помечено входным символомх, выходным символомуи направлением движения головкиD(рис.5.2).
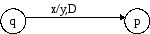
Рис.5.2. Графическое представление команды машины Тьюринга <(q,x)(p,y,D)>
Именно эта последняя деталь (указание направления движения головки) отличает граф переходов МТ от графа переходов конечного автомата.
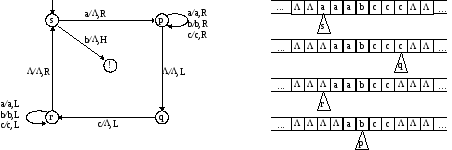
Рис.5.3. Граф переходов машины Тьюринга, распознающей язык, и несколько ее конфигураций при обработке входной цепочки“aaabccc”.
Начальная конфигурация этой МТ (когда она находится в начальном состоянии s, а головка расположена против крайнего левого символа входной цепочки) и несколько промежуточных конфигураций, возникающих при ее работе (рис. 5.3), поясняют алгоритм распознавания.
Пример 5.2. Рассмотрим машину Тьюринга, находящую наибольший общий делитель двух положительных целых чисел, заданных в унарной системе счисления, в которой числуNсоответствуетNпоследовательных символов‘1’. Начальная конфигурация машины Тьюринга пусть будет такова:
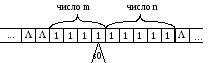
Программу этой машины Тьюринга зададим с помощью графа переходов:
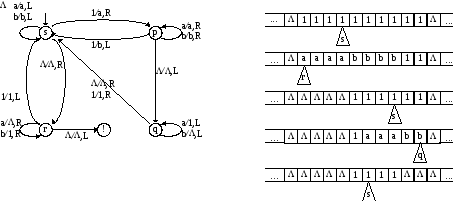
Рис.5.4. Граф переходов машины Тьюринга, вычисляющей НОД двух чисел, и несколько ее конфигураций при обработке пары чисел(4,6)
Стратегия вычисления НОД двух чисел здесь — это повторяющиеся действия по нахождению меньшего из двух чисел и вычитанию его из большего до тех пор, пока не получатся равные числа. Алгоритм работы этой МТ поясняется последовательно возникающими ее конфигурациями при обработке входа (4,6) на рис.5.4.
Рассмотрим несколько свойств машин Тьюринга.
Теорема 5.1.Для любой машины Тьюринга существует эквивалентная машина Тьюринга, такая, что все ребра, входящие в каждую вершину, помечены одним и тем же направлением движения головки.
Доказательстволегко следует из правила эквивалентного преобразования исходной машины Тьюринга:
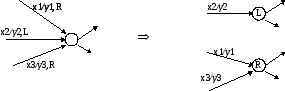
Каждое состояние исходной МТ расщепляется на несколько эквивалентных состояний, в каждое из которых приходят ребра только с одинаковой пометкой о направленности движения головки.
Теорема 5.2.Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.
Доказательствоэтой теоремы конструктивное, т.е. мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, т.е. определим новое расположение информации на ленте:

Затем перенумеруем ячейки, причем будем считать, что символ “*” не содержится в словаре МТ:
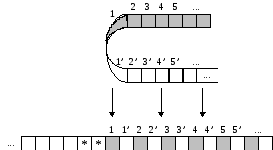
Наконец, изменим машину Тьюринга, удвоив число ее состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна ее работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ‘*’, значит головкасчитывания-записи достигла границы зоны:
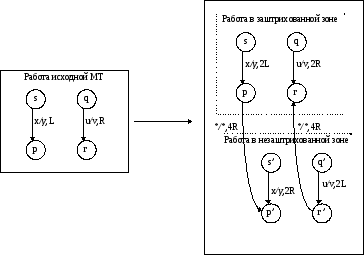
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров “*” лента в эквивалентной машине Тьюринга не используется.
Источник: studfile.net
Машина Тьюринга. Машина Поста

Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

абстрактная схема машины Тьюринга
В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
Машина Поста
Машина Поста – это абстрактная (несуществующая реально) вычислительная машина, созданная для уточнения (формализации) понятия алгоритма. Представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы.
В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой. Если задача имеет алгоритмическое решение, то она представима в форме команд для машины Поста.
Машина Поста состоит из …
1. бесконечной ленты, поделенной на одинаковые ячейки (секции). Ячейка может быть пустой (0 или пустота) или содержать метку (1 или любой другой знак),
2. головки (каретки), способной передвигаться по ленте на одну ячейку в ту или иную сторону, а также способной проверять наличие метки, стирать и записывать метку.
Текущее состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты – информация о том, какие секции пусты, а какие отмечены. Шаг – это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы.
Кареткой управляет программа, состоящая из строк команд. Каждая команда имеет следующий синтаксис:
I K j,
где i — номер команды, K – действие каретки, j — номер следующей команды (отсылка).
Всего для машины Поста существует шесть типов команд:
· V j — поставить метку, перейти к j-й строке программы.
· X j — стереть метку, перейти к j-й строке программы.
· -> j — сдвинуться вправо, перейти к j-й строке программы.
· ? j1; j2 — если в ячейке нет метки, то перейти к j1-й строке программы, иначе перейти к j2-й строке программы.
· ! – конец программы (стоп).
У команды «стоп» отсылки нет.
Варианты окончания выполнения программы на машине Поста:
1. Команда «стоп» — корректная остановка. Возникает в результате выполнения правильно написанного алгоритма.
2. Выполнение недопустимой команды – нерезультативная остановка. Случаи, когда головка должна записать метку там, где она уже есть, или стереть метку там, где ее нет, являются аварийными (недопустимыми).
3. Уход в бесконечность, зацикливание. Машина Поста в результате работы алгоритма может вообще не остановиться (никогда не дойти до команды «стоп» и никогда не завершиться аварийной ситуацией).
Элементарные действия (команды) машина Поста проще команд машины Тьюринга. Поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга.
Почему достаточно лишь два различных символа (есть метка, нет метки)? Дело в том, что любой алфавит может быть закодирован двумя знаками; в зависимости от алфавита возрастать может только количество двоичных символов в букве алфавита.
Лекция №4.Основы алгоритмизации и программирования. Основные конструкции программирования
План лекции
1. Стратегия решения задач и поиск решений
2. Концепции и свойства алгоритмов, реализации алгоритмов
3. Блок-схемы как графическая реализация алгоритмов
4. Основные конструкции программирования
Ключевые слова:алгоритм, свойства, классификация, прогаммирование, конструкция.
Иллюстративный материал:Электронный учебник, слайд, схема.
Источник: megaobuchalka.ru
Презентация на тему Машина Тьюринга

описать как последовательность действий, выполняемых машиной Тьюринга или машиной Поста, то эта задача алгоритмически разрешима.

Слайд 3Чтобы формально описать понятие алгоритма нужно:
с какими объектами работает любой алгоритм
2.Формально описать
действия над этими объектами и порядок выполнения этих действий

Слайд 41. Уточнение того, с какими объектами работают
алгоритмы
Любые объекты (числа, формулы, слова,
шахматные фигуры и пр.) можно описать на некотором языке т.е представить как последовательность символов некоторого алфавита
Задача любого алгоритма: преобразовать сообщение, записанное в некотором алфавите в другое сообщение

Слайд 5 Объекты реального мира можно изображать
словами в различных алфавитах. Это позволяет считать,
что объектами работы алгоритмов могут быть только слова.
Посредством кодирования входного алфавита, любой алгоритм можно свести к алгоритму над словами в алфавите .

Слайд 62. Формальное описание действий над объектами-словами и
порядка выполнения этих действий
Пусть исходные
данные представлены с помощью алфавита А и образуют конечную последовательность знаков (слово).
В результате выполнения алгоритма сформируется новое слово, возможно составленное из знаков другого алфавита В
Чтобы произвести такое преобразование машина должна уметь осуществлять следующие элементарные действия:
Двигаться вдоль слова вправо и влево
Считывать (распознавать) знак
Заменять один знак исходного слова ai знаком bi из алфавита B
Удалять знак исходного алфавита
Добавлять к исходному слову знак из алфавита В
Останавливаться
Источник: thepresentation.ru