Машина тьюринга код программы

Здесь мы создадим минималистическую машину Тьюринга на языке программирования Python, которая может выполнять любую заданную программу. Для примера мы дадим ей программу добавления единице к данному числу, представленному последовательностью единиц.
Вот эта машина и её вызов с программой и входной лентой в качестве параметров:

На выходе машина напечатает:

[0, 0, 0, 1, 1, 1, 1, ‘0’, ‘0’]

Это та же лента, которую мы дали на входе, только на ней на одну единицу больше.

Обратите внимание, что машина Тьюринга в этой программе, конечно, не совсем закончена: она не умеет работать с бесконечной лентой, и её алфавит состоит только из двух символов — 0 и 1. Но не будем слишком усложнять.
Программа в конце этой страницы снабжена подробными комментариями для желающих получше в ней разобраться.

Дан алфавит из двух символов: 0 и 1. Бесконечная лента заполнена нулями и только в одном месте находится строка из нескольких единиц (число их неизвестно). Дано, что в самом начале управляющее устройство (далее — УУ) находится где-то слева от строки с единицами. Машина должна найти на ленте эту строку и добавить справа от неё ещё одну единицу.

Теория алгоритмов: машина Тьюринга

Задание станет совершенно понятно, если вы посмотрите на рисунок:

Почему в формулировке задачи мы постановили, что УУ находится слева от строки с единицами, а не в произвольном месте ленты ? Дело в том, что, если бы мы были вынуждены искать единицы по всей ленте (то есть в обоих направлениях), задача усложнилась бы многократно! Более того, было бы крайне тяжело обойтись только двумя символами алфавита. Поэтому остановимся на гораздо более простой формулировке задачи, и попробуем разработать стратегию решения.

Естественно, что в самом начале УУ начинает двигаться вправо и сканировать содержимое клеток ленты. Если УУ видит в клетке ноль, оно оставляет всё как есть и делает один шаг вправо. Если УУ видит в клетке единицу, оно оставляет всё как есть и делает один шаг вправо. Постойте!

В чём же разница между двумя действиями, которые совершает УУ в случае чтения нуля и в случае чтения единицы ? Верно — разницы в поведении УУ нет, но есть более существенная разница — в поведении самой Машины Тьюринга, вернее, программы, которая управляет УУ. Дело в том, что изначально наша Машина находится в некоем состоянии (назовём его состояние А), которое можно охарактеризовать так: ищи строку единиц справа от УУ. В тот момент, когда УУ считывает единицу, Машина переходит в состояние В, которое означает: а теперь ищи самую последнюю (самую правую) единицу в строке единиц. При этом УУ совершает те же самые действия, только находясь в другом состоянии.

Итак, находясь в состоянии B, машина продолжает двигаться вправо, сканируя ленту. Наконец, УУ обнаруживает в клетке ноль (это может случиться как на следующем ходу, так и через целый гугл клеток). Этот ноль означает, что строка единиц кончилась и пришло время добавить новую единицу. УУ заменяет этот ноль на единицу и останавливается. При этом, мы можем оставить машину в состоянии В, но более красивым вариантом будет перевести её в состояние С, который будет «тупиком» — это состояние будет означать остановку машины.

Машина тьюринга на C++/Qt

Задача выполнена. Теперь, чтобы построить управляющую таблицу (проще говоря — программу) Машины Тьюринга, призовём на помощь диаграмму, так называемый «конечный автомат»:

На этой диаграмме изображены три только что описанных состояния. Во многом она говорит сама за себя, и в объяснении нуждаются только подписи под стрелками перехода из одного состояния в другое. Так 0 -> 0 / Right обозначает: если УУ видит в клетке 0, оно должно заменить его на 0 и сдвинуться вправо. Таким образом, 0 -> 1 / Stop значит: если в клетке 0, замени его на 1 и не двигайся.

Всё предельно просто. Теперь нам осталось только перевести диаграмму состояний в таблицу управления и Машина Тьюринга, решающая поставленную задачу, готова!

А вот и таблица:

Как видите, состояние С — это полный тупик. Машина ничего не меняет и никуда не двигается. Более того, из этого состояния нет выхода ни в какое другое.

И чтобы рассеять последние сомнения, приведём последовательность шагов и состояний, в которых будет пребывать наша Машина, решая поставленную задачу:

Ещё раз та же программа, на этот раз с подробными комментариями:

Источник: www.samovar.ltd

Визуализация машины Тьюринга средствами СИ/С++

Визуализация машины Тьюринга средствами СИ/С++ / Е. В. Коптенок, Б. А. Корж, М. Ю. Пескова [и др.]. — Текст : непосредственный // Исследования молодых ученых : материалы VII Междунар. науч. конф. (г. Казань, февраль 2020 г.). — Казань : Молодой ученый, 2020. — С. 3-6. — URL: https://moluch.ru/conf/stud/archive/361/15617/ (дата обращения: 01.07.2023).

В данной статье описана реализация симулятора машины Тьюринга средствами C++ с использованием визуальной библиотеки Qt. Приложение может быть полезно всем, кто изучает информатику, теорию вычислений и алгоритмов, так как с его помощью можно лучше понять устройство машины Тьюринга — одной из фундаментальных математических концепций в информатике.

Существует большое количество похожих реализаций, большинство из них выполнено в виде веб-приложений. Главная особенность моей реализации в том, что она является десктопным приложением. Благодаря этому достигается более высокая отзывчивость и скорость работы. Однако, приложение не проигрывает в универсальности своим веб-аналогам, так как может выполняться на большинстве современных операционных систем.

Машина Тьюринга — это абстрактная вычислительная машина, предложенная математиком Аланом Тьюрингом в 1936 году для формализации понятия алгоритма. Согласно тезису Чёрча-Тьюринга, машина способна имитировать всех исполнителей, каким-либо образом реализующих в котором каждый шаг вычисления достаточно элементарен.

Машина Тьюринга состоит из двух частей — ленты и автомата. Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые никак не нумеруются и не именуются. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться — в неё можно записать другой символ или стереть находящийся в ней символ.

В начале выполнения машина находится в некотором состоянии, определенном пользователем. Каретка, в зависимости от своего состояния и содержимого текущей ячейки, выполняет действия, определенные соответствующей строчкой кода: записывает в ячейку новый символ, переходит в следующее состояние и выполняет смещение (переходит либо на следующую ячейку, либо на предыдущую, либо стоит на месте). Этот процесс происходит до тех пор, пока не будет достигнуто одно из нескольких состояний, отмеченных пользователем как терминальные.

Интерфейс программы представлен на рис. 1.

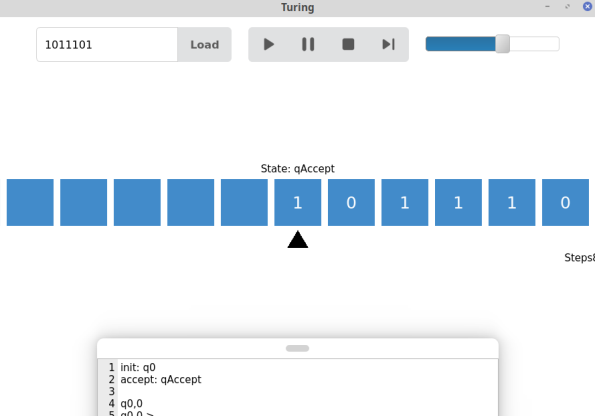
Рис. 1. Внешний вид программы

Чтобы запустить машину Тьюринга, пользователь сперва должен ввести в поле редактора кода (см. рис. 2) текст программы, и нажать кнопку «Компилировать». Если программа была скомпилирована успешно, можно загружать исходные данные на ленту, с помощью поля ввода в верхнем левом углу и кнопки «Load».

После этого можно запустить выполнение программы нажатием кнопки «Пуск» (первая слева), и затем контролировать выполнение программы кнопками «Пауза», «Стоп», «Шаг вперед». Ползунок справа позволяет изменять скорость выполнения программы прямо во время выполнения.

Компилятор уведомляет пользователя о синтаксических ошибках в программе, указывая место, где была допущена ошибка, и ее предполагаемый тип (рис. 3).

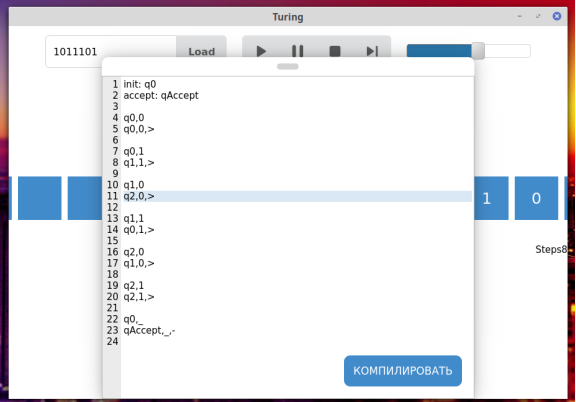
Рис. 2. Редактор кода

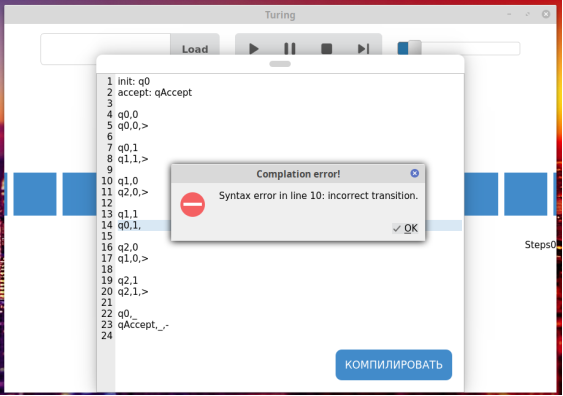
Рис. 3. Уведомление о синтаксической ошибке

Так как машины описывается конечным числом состояний, программа должна включать в себя следующие строчки.

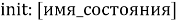
1. Начальное состояние. Синтаксис:
2. Список терминальных состояний. Синтаксис:

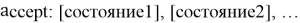
1. Список возможных условий. Каждое условие описывается двумя последовательными строками кода, их синтаксис выглядит следующим образом:

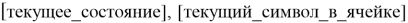
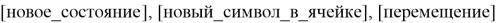
Где [перемещение] — это один из трех символов: “ ” — на ячейку вправо,”-” — остаться на месте.

На рис. 4. представлен текст программы, которая проверяет делимость двоичного числа на 3. Это простейшая программа, которая может стать хорошей иллюстрацией возможностей симулятора.

Рис. 4. Текст программы, которая проверяет делимость двоичного числа на 3

В данной статье был рассмотрен завершенный и готовый к использованию программный продукт, который может быть использован в образовательных целях. Исходный код программы распространяется по открытой лицензии GNU GPLv2 и размещен на Github, поэтому его может использовать и улучшать любой желающий. У меня есть некоторые идеи по дальнейшему улучшению проекта.

Возможно, в будущем будет добавлен статический анализатор кода программы, каталог примеров программ. Также многие проекты-аналоги умеют работать с несколькими лентами (концепция машины Тьюринга допускает такие модификации). Это могло бы стать следующим шагом в развитии проекта.

1. B. Jack Copeland. The Essential Turing: Seminal Writings in Computing, Logic, Phi-losophy, Artificial Intelligence, and Artificial Life plus The Secrets of Enigma / Claren-don Press (Oxford University Press), Oxford UK, 2013
2. Павловская, Т. А. C/C++. Процедурное и объектно-ориентированное программи-рование / Т. А. Павловская. — СПб.: Питер, 2015. — 496 с.
3. Qt Documentation [Электронный ресурс]. — Режим доступа: https://doc.qt.io/ сво-бодный (01.06.2019).
4. Орлов. С. Программная инженерия. Технологии разработки программного обеспечения / С. Орлов — СПб.: Питер, 2018–640с.
5. Eckel B. Thinking in C++. / Bruce Eckel — Prentice Hall, 1995.
6. Stroustrup B. The C++ Programming Language. / Bjarne Stroustrup — Addison-Wesley, 1985.

Основные термины (генерируются автоматически): машина Тьюринга, текст программы, GNU, выполнение программы, двоичное число, символ.

Похожие статьи

Применение машины Тьюринга для реализации алгоритмов.

Программа для машины Тьюринга. Сама по себе МТ ничего не делает. Для того, чтобы заставить её работать, надо написать для неё

После этих предварительных действий начинается выполнение программы. В таблице отыскивается ячейка на пересечении первой.

Зарождение и золотой век искусственного интеллекта

Машина Тьюринга — это абстрактная вычислительная машина, созданная для формализации понятия алгоритма.

В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на.

Основные этапы развития искусственного интеллекта

Машина Тьюринга — это абстрактная вычислительная машина, созданная для формализации понятия алгоритма.

В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на.

Программы для электронно-вычислительных машин как объект.

Программы для электронных вычислительных машин (далее — программы для ЭВМ ) можно отнести к одним из самых молодых.

2. Предоставление экземпляров программы для ЭВМ или базы данных неопределенному кругу лиц , в том числе путем записи в память ЭВМ .

Разработка устройства преобразования 12-разрядного двоичного.

В данной статье представлена разработка устройства преобразования 12-разрядного двоичного кода в двоично-десятичный с индикацией полученных чисел. Ключевые слова: двоично-десятичный код, двоичный код, индикатор, индикация.

Разработка способа представления длинных чисел в памяти.

Закрытое ПО: большинство программ, реализующих вычисления неограниченно больших чисел с любой точностью разрабатываются для шифрования и кодирования и не находятся в открытом доступе. Разработанный программный продукт устраняет большинство недостатков доступных.

Анализ применения гомоморфных схем шифрования в алгоритмах.

Ограничение на работу с целыми числами, количество возможных операций сложения и умножения из-за возрастающего криптографического шума, означает, что на практике гомоморфное шифрование позволяет работать только над зашифрованными данными.

Обзор систем машинного перевода | Статья в журнале.

В данной статье рассмотрены основные виды систем машинного перевода. Рас-смотрены основные системы машинного перевода, произведено их сравнение и анализ. Сделаны предположения о возможных путях развития подобных систем.

Источник: moluch.ru

Машина Тьюринга на шаблонах

Каждый интересующийся шаблонами в С++ скорее всего слышал об их Тьюринг-полноте и связанных с этим шутках про «we put a language in your language, so you can program while you program». В этом посте я расскажу как с помощью шаблонов и константных выражений построить настоящую машину Тьюринга, вычисляющую результат своей работы во время компиляции, на которой можно будет запускать уже существующие программы. Например усердный бобер с 4 состояниями и 2 символами выглядит как-то так:

ADD_STATE(A); ADD_STATE(B); ADD_STATE(C); ADD_STATE(D); ADD_RULE(A, Blank, 1, Right, B); ADD_RULE(A, 1, 1, Left, B); ADD_RULE(B, Blank, 1, Left, A); ADD_RULE(B, 1, Blank, Left, C); ADD_RULE(C, Blank, 1, Right, Stop); ADD_RULE(C, 1, 1, Left, D); ADD_RULE(D, Blank, 1, Right, D); ADD_RULE(D, 1, Blank, Right, A); using tape = Tape; using machine = Machine; using result = Run::type; int main()

На выходе, как и положено, получаем
1 _ 1 1 1 1 1 1 1 1 1 1 1 1

Тут можно посмотреть на код: https://ideone.com/MvBU3Z. Желающие узнать как все устроено внутри, добро пожаловать под кат.

Для полноценной работы машины Тьюринга (МТ далее) нужно следующее:
1. Лента с символами
2. Способ считывать и записывать символы на ленту
3. Способ перемещаться по ленте и расширять ее по мере надобности
4. Система состояний и правил перехода
5. Способ вычислять следующее состояние системы целиком (машина + лента)
6. Способ останавливать выполнение, когда машина достигает финального состояния

Все операции должны выполняться над типами и константными выражениями, а не над переменными как в обычной жизни. Для согласованности со стандартной библиотекой С++, мы будем использовать следующий способ вычислений:

// объявление операции template class Operation; // специализация операции для конкретного типа template class Operation < public: // тип, содержащий результат операции using type = typename Output; >

Использование имени «type» для хранения результатов сделает возможным некоторые полезные трюки с std::conditional и std::integral_constant, которые мы увидим в далнейшем.

1. Так как МТ использует конечный алфавит, мы можем без потери общности считать, что символы на ленте представлены целыми числами. Договоримся, что по умолчанию лента содержит символ, заданный константой Blank, равной -1. При желании это значение можно легко изменить.

constexpr int Blank = -1; template class Tape < public: using type = Tape; constexpr static int length = sizeof. (xs); >;

Что можно сделать с лентой? Можно ее, например, вывести на экран. Функция print будет единственной функцией в обычном понимании, которая будет использоваться в программах для нашей машины.

template void print(T); template<> void print(Tape<>) < std::cout template void print(Tape) < if (x == Blank) < std::cout else < std::cout print(Tape()); >

Здесь используется стандартный трюк с рекурсивным шаблоном. По ссылке можно посмотреть на получившийся код: https://ideone.com/DBHSC6

2. Прежде чем перейти к чтению и записи, необходимо сделать некоторые вспомогательные операции:

template class Concatenate; template class Concatenate, Tape> < public: using type = Tape; >;

С конкатенацией все просто.
template class Invert; template<> class Invert> < public: using type = Tape<>; >; template class Invert> < public: using type = typename Concatenate< typename Invert>::type, Tape >::type; >;

Инверсия чуть-чуть посложнее: берем первый символ, переносим его в конец и конкатенируем с перевернутым хвостом. Внутри разворачивается рекурсия в результате которой получается то, что нам нужно. Вот пример запуска: https://ideone.com/47GKNp

Чтение символов — место, где начинается магия со стандартной библиотекой.

template class Read; template class Read> < public: using type = typename std::conditional< (n == 0), std::integral_constant, Read> >::type::type; >;

Логика на самом деле относительно проста: если n == 0, мы возвращаем первый символ ленты, обернутый в std::integral_constant, в противном случае мы уменьшаем n на единицу и отбрасываем первый символ. Для чего нужна конструкция ::type::type? Первый type относится к std::conditional. std::conditional::type равняется A, если T == true, и равняется B в остальных случаях. Таким образом, в зависимости от значения n, вся конструкция развернется в одно из следующих выражений:

using type = std::integral_constant::type; using type = Read>::type;

Первая строчка эквивалентна type = std::integral_constant, вторая вызовет рекурсию. Но почему нельзя было написать этот код вот так:

template class Read> < public: using type = typename std::conditional< (n == 0), std::integral_constant, typename Read>::type >::type; >;

Разгадка: в первом случае шаблон Read> будет инстанциирован в зависимости от значения n, во втором он будет инстанциирован всегда, так как мы явно используем внутренний alias (::type). Если мы всего лишь упомянем имя шаблона, он не будет инстанциирован, если мы попытаемся использовать что-то из его внутренностей, шаблон будет инстанциирован. Таким образом, выражение из второго примера приведет к бесконечной рекурсии, которая все же остановится, но с ошибкой. Этот примем с ::type::type будет активно использоваться в дальнейшем.
Тут можно посмотреть на пример чтения с ленты: https://ideone.com/vEyASt

Запись. Допустим мы хотим записать на ленту вместо символа х символ y. Операцию записи можно представить как деление всей ленты на часть до х, сам символ х и часть после х, замену x на y и конкатенирование всех частей обратно в целое. Определим операции для вычисления n первых и последних символов:

template class NLast; template class NLast> < public: using type = typename std::conditional< (n == sizeof. (xs)), Tape, NLast >::type::type; >; template class NFirst; template class NFirst < public: using type = typename Invert< typename NLast< n, typename Invert::type >::type >::type; >;

Чтобы получить n последних символов, будем делать примерно то же, что делали для чтения: укорачивать ленту по одному символу, пока длина оставшегося куска не станет равна n. Чтобы получить первые n символов, перевернем ленту, возьмем последние n символов и перевернем результат. Примеры использования: https://ideone.com/igYF3W.

Наконец, непосредственно запись:

template class Write; template class Write> < public: using type = typename Concatenate< typename Concatenate< typename NFirst>::type, Tape >::type, typename NLast<(sizeof. (xs) — pos — 1), Tape>::type >::type; >;

Этот код не сложно понять, зная, что тут на самом деле происходит. Примеры записи: https://ideone.com/w2mUdh

В данный момент мы имеем класс для представления ленты, а также умеем читать и писать символы. Теперь нужно научиться двигать ленту.

3. Наша МТ будет поддерживать следующие операции передвижения: Hold, Left and Right. Каждая из них должна уметь вычислять следующую позицию и следующее состояние ленты, зная текущее ее состояние и позицию. Если машина смотрит на символ в позиции 0 и мы хотим сдвинуть ее влево, ленту необходимо расширить. Аналогично в случае, когда машина смотрит на конечный символ и двигается вправо.

template class Hold; template class Hold> < public: constexpr static int position = pos; using tape = Tape; >; template class Left; template class Left> < public: constexpr static int position = typename std::conditional< (pos >0), std::integral_constant, std::integral_constant >::type(); using tape = typename std::conditional < (pos >0), Tape, Tape >::type; >; template class Right; template class Right> < public: constexpr static int position = pos + 1; using tape = typename std::conditional< (pos < sizeof. (xs) — 1), Tape, Tape >::type; >;

4. Теперь можно переходить к состояниям. Если машина находится в каком-то состоянии и читает символ с ленты, нам нужно знать три вещи: что писать, куда двигаться и в какое состояние перейти. Состояния решено было запрограммировать как группу специализаций шаблонов, где каждая специализация соответствует паре (состояние, символ), то есть правилу перехода. Предположим, мы хотим задать следующее правило: находясь в состоянии A и прочитав символ 0, нужно записать вместо него 1, сдвинуться вправо и перейти в состояние B. Выглядеть это правило будет вот так:

template<> class A < public: constexpr static int write = 1; templateusing move = Right; template using next = B; >;

Здесь использована отличная возможность современного С++: alias template. Поля «move» и «next» не просто типы, а шаблоны типов, в дальнейшем они будут использованы МТ для вычисления своего следующего состояния. Писать такую конструкцию для каждого правила довольно утомительно, поэтому обернем задание правил перехода в макрос. Состояние, перейдя в которое машина должна остановиться, назовем Stop.

5. Чтобы удерживать состояние всей системы (состояние машины, ее текущая позиция и состояние ленты), определим класс Machine. Единственное, что должен уметь этот класс — делать один шаг симуляции, вычислять свое следующее состояние.

template class State, int pos, int. xs> class Machine> < constexpr static int symbol = typename Read>::type(); using state = State; template using nextState = typename State::template next; using move = typename state::template move; constexpr static int nextPos = move::position; using modifiedTape = typename Write>::type; using nextTape = typename move::tape; public: using step = Machine; >;

Сперва мы считываем символ с ленты и сохраняем его как «symbol». Далее мы инстанциируем класс State с конкретным значением символа и получаем правило перехода. Следующее состояние машины определяется следующим образом:

template using nextState = typename State::template next;

Зачем нужно ключевое слово «template» перед «next»? Согласно стандарту, перед именем вложенного шаблона необходимо писать «template», если это имя используется после оператора разрешения области видимости(«::»). При вычислении операции перемещения можно наблюдать тот же эффект.

Чтобы вычислить следующее состояние ленты, запишем в нее новый символ и по необходимости расширим, последовательно вызвав операции записи и перемещения. Вычисление новой позиции очевидно.

Наконец, все готово, и мы умеем вычислять следующее состояние системы, делать шаги. Можно написать временную вспомогательную функцию для вывода состояния машины, придумать какую-нибудь простую программу и пошагово следить за ее выполнением: https://ideone.com/XuBDry. В этом примере можно наблюдать, как машина движется право и заменяет все на своем пути.

6. Все выглядит так, как будто работает, но мы должны идти глубже: входными данными для процесса являются начальное состояние машины, ее позиция и состояние ленты, в конце мы хотим знать только что случилось с лентой, когда машина достигла состояния Stop. Окей, напишем класс

template class Run; template class State, int pos, int. xs> class Run>> < using step = typename Machine>::step; public: using type = typename std::conditional< std::is_same, Stop>::value, Tape, Run >::type::type; >;

Чтобы проверить условие остановки, мы инстанциируем текущее состояние машины и состояние Stop со значением 0, после чего сравниваем их между собой посредством std::is_same. Если они равны, возвращаем ленту, в противном случае делам следующий шаг и снова проверяем условие остановки.

Попробуем теперь написать что-нибудь. Например увеличение чисел в бинарном формате. Предположим, что число записано слева направо, как на бумажке.

ADD_STATE(S0); ADD_STATE(S1); ADD_STATE(S2); ADD_RULE(S0, Blank, Blank, Left, S1); ADD_RULE(S0, 0, 0, Right, S0); ADD_RULE(S0, 1, 1, Right, S0); ADD_RULE(S1, Blank, 1, Right, S2); ADD_RULE(S1, 0, 1, Left, S2); ADD_RULE(S1, 1, 0, Left, S1); ADD_RULE(S2, Blank, Blank, Hold, Stop); ADD_RULE(S2, 0, 0, Right, S2); ADD_RULE(S2, 1, 1, Right, S2); using tape = Tape; using result = Run>::type; int main()

https://ideone.com/AgK4nx. Что делать, если хочется запустить инкеремент несколько раз? Конечно же написать отдельный класс операции и несколько раз его вызвать, все просто:

template class Increment < >; template class Increment> < public: using type = typename Run::length — 1, Tape>>::type; >; using tape = Tape; int main() < print(tape()); print(Increment::type()); print(Increment::type()); print(Increment::type>::type()); print(Increment::type>::type>::type()); print(Increment::type>::type>::type>::type()); return 0; >

Источник: habr.com