Приветствую всех.
Продолжаю написание статей про простейшие логические цепи.
В этом посте – правила соединения логических элементов и цепей между собой, а также два простых метода анализа логических схем.
По многочисленным просьбам хабралюдей, а также для упрощения восприятия написанного, буду кроме западного названия определённого элемента приводить и русское.
Правила соединения цепей и их компонентов
В прошлой статье мы познакомились с такими логическими модулями, как Not-1 (логическое отрицание, !A), Or-2 (логическая сумма, AvB) и And-2 (логическое умножение, A^B), но ни слова не было сказано о том, как соединять между собой эти простейшие комбинационные логические цепи (КЛЦ, они же – комбинационные схемы).
Вот несколько правил, которые помогут избежать ошибок при соединении проводников и логических модулей:
1. Не соединяйте два выхода напрямую. Это может привести к конфликту сигналов.
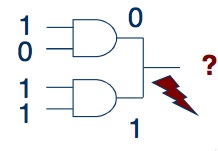
Построение логических схем
2. Если у логического модудя два входа, они оба должны иметь значение. Если неизвестен сигнал на одном из входов, то скорее всего не получится узнать значение исходящего сигнала.
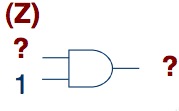
3. Не должно быть циклов. Эффект может быть любым – от нестабильности работы цепи до её неспособности функционировать.

Анализ логических схем
Для упрощения анализа цепей мы будем использовать некоторые условные обозначения. Например:
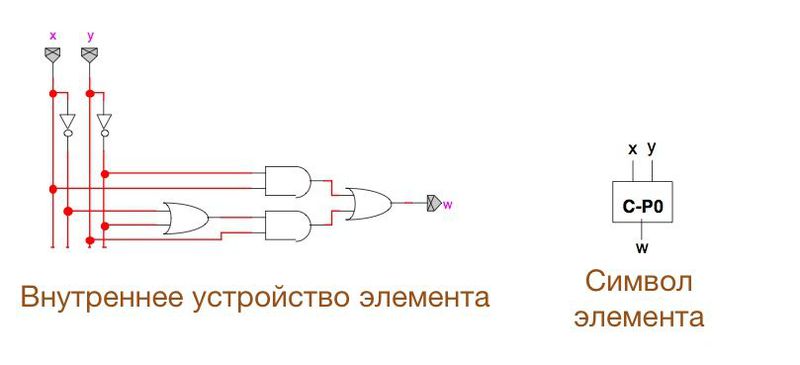
Как видите, определённый набор элементов изображается с помощью одного-единственного модуля.
Анализ цепи из 6-8 элементов
Возьмём любую сделанную по правилам комбинационную схему. Например вот эту:
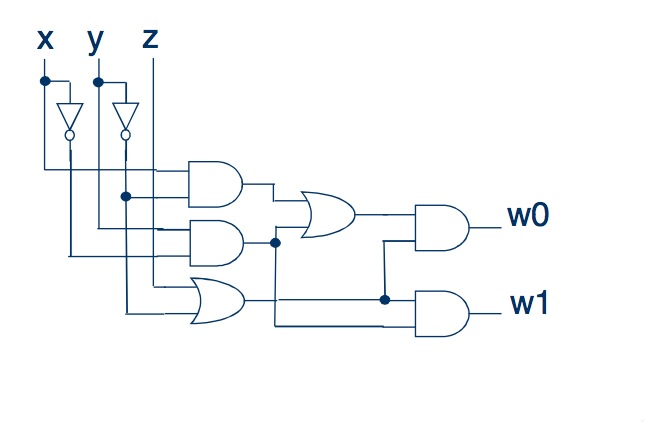
Если вам по каким-то причинам не нравится моя схема, нарисуйте свою 🙂
Суть анализа цепи заключается в выявлении исходящих сигналов в зависимости от значений входов.
Существует два метода этого самого анализа – горизонтальный (по строкам) и вертикальный (по столбцам).
Анализ по строкам
Этот тип исследования цепей заключается в следующем: мы поочерёдно выставляем разные значения на входах цепи, и смотрим, как изменяется сигнал во время его прохождения дальше по цепи. Вот наглядный пример:
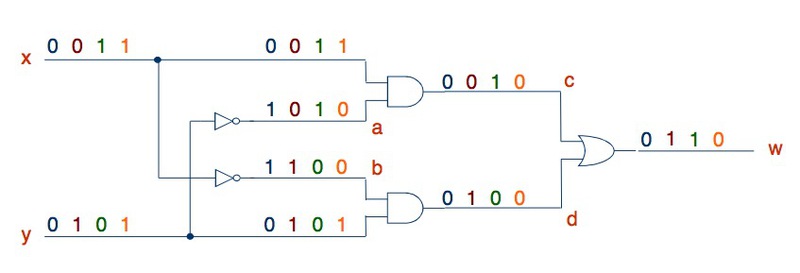
Таким способом удобно анализировать небольшие схемы с одним-двумя входами, потому что не обязательно строить таблицу истинности.
Для таких цепей, как выбранная нами ранее, лучше всё-таки нарисовать эту самую таблицу и вписывать туда найденные значения. Вот так, например:
Логические выражения, таблицы истинности ,структурная логическая схема
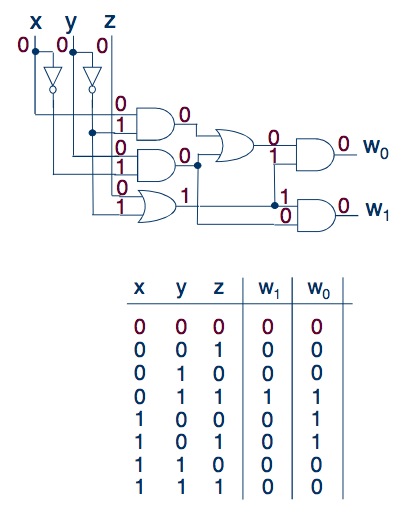
Анализ по столбцам
Суть этого метода – поочерёдно, с помощью логических выражений, найти значения для всех частей цепи, и только потом вычислить результат для выходов цепи.
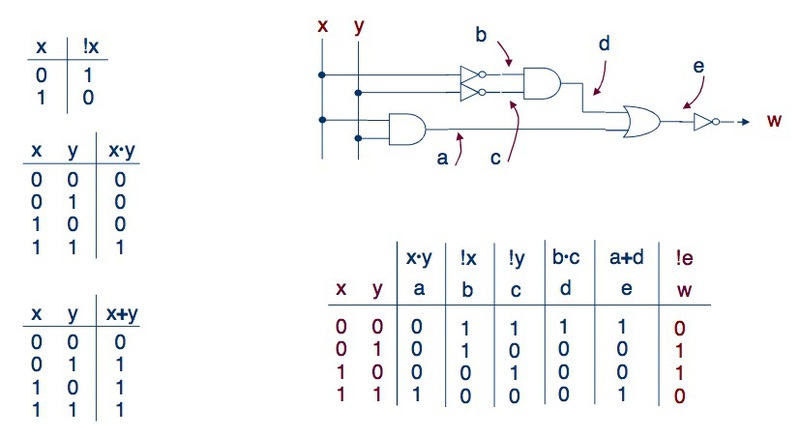
Как видно на картинке, мы вычисляем значения сигнала для каждого элемента цепи, постепенно приближаясь к выходу. Для нашей цепи это будет выглядеть так:
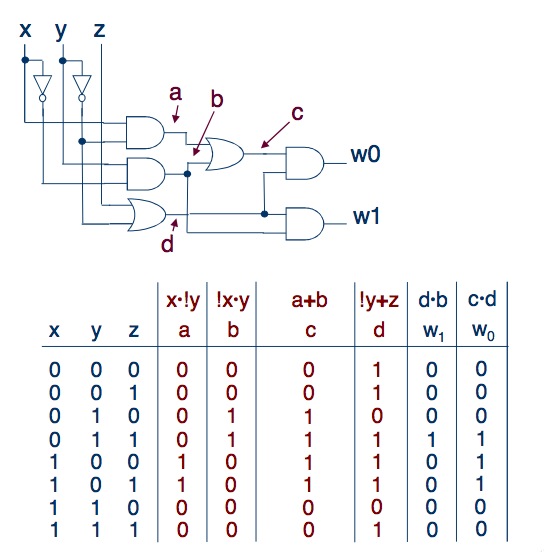
Теперь можно сравнить результаты, полученные с помощью двух методов. Если они совпадают, то это значит, что либо всё сделано правильно, либо мы допустили больше одной ошибки ( 😀 ).
На данный момент всё.
В следующей статье мы начнём создавать свои логические схемы по заданным параметрам.
Продолжение будет очень скоро.
Спасибо за внимание, и хороших всем выходных!
Источник: habr.com
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
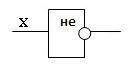
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
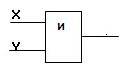
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
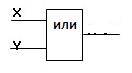
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Пример 1.
Составьте логическую схему для логического выражения: F=A / B / A.
1. Две переменные – А и В.
2. Две логические операции: 1-/, 2-/.
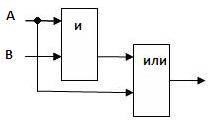
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: / и две /; А/В/ ¬ (В/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
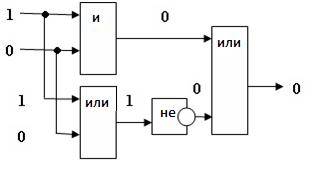
4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0
- Теория
- Формы мышления
- Алгебра высказываний
- Логические функции
- Таблица истинности и логические выражения
- Законы алгебры логики
- Решение логических задач
- Логические основы работы компьютера
- Психология
- Психология отношений
- Формы мышления
- Алгебра высказываний
- Логические функции
- Таблица истинности и логические выражения
- Законы и правила преобразования логических выражений
- Решение логических задач
- Логические основы устройства компьютера
- Формы мышления
- Алгебра высказываний
- Тренировка по теме «Логические функции»
- Логические выражения и таблица истинности
- Законы и правила преобразования логических выражений
- Решение логических задач
- Логические основы работы компьютера
- Формы мышления
- Алгебра высказываний
- Логические функции
- Таблица истинности и логические выражения
- Законы и правила преобразования логических выражений
- Решение логических задач
- Логические основы работы компьютера
Источник: mir-logiki.ru
Логические уравнения и программы и их схемы
Логические схемы нужны для того чтобы в наглядной графической форме отобразить последовательность выполнения операций при вычислении логических формул.
Входящие слева линии и цифры около них обозначают значения операндов, линия справа и соответствующая цифра — результат операции (значение на выходе логических элементов).
Логические схемы базовых логических операций
Схема «И» — э то схема , реализу ющая ко нъюнкцию двух или более логических значений.
Единица на выходе с хемы «И» будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = xИЛИ» — э то схема, реализующая дизъюнкцию двух или более логических значений.
Когда хотя бы на одном входе схемы «ИЛИ» будет единица, на её выходе также будет единица.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y.
Схема «НЕ» (инвентор) — схема,
реализующая операцию отрицания.
Если на входе схемы 0, то на выхо де 1. Когда на входе 1, на выходе 0 .
Связь между входом x этой схемы и выходом z можно записать соотношением z = ¬x.
Построение логических схем
Правило построения логических схем:
1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей вентиль (базовый логический элемент).
4) Соединить вентили в порядке выполнения логических операций.
Составить логическую схему для логического выражения: F=A v B , 2-v.
Строим схему:
Постройте логическую схему, соответствующую логическому выражению F=А
Логических операций три: Аhttps://www.sites.google.com/a/gkl-kemerovo.ru/informatics/logic/5″ target=»_blank»]www.sites.google.com[/mask_link]