В статье «Алгебра логики» мы выучили основы этого непростого раздела математики. Разобравшись в той теме, пора пойти дальше и заговорить на понятном компьютеру языке — языке программирования.
Логические уравнения в Python
Как логические операторы записываются в программе Python и в чем их отличие?
Логические операторы в Python мы уже упоминали в статье «Основы программирования. Часть 2». Давайте их вспомним:
Проблема в том, что для импликации и эквиваленции нет специальных логических операторов, но для них можно использовать математические:
— Математическое сравнение на равенство работает также, как логическая эквиваленция: вернет True, если значения будут одинаковые и False в противном случае.
— Математическое “меньше или равно” полностью соответствует логическому следованию: False будет возвращено только в том случае, если значение слева будет меньше или равно значению справа. А если вспомнить аналогию логических переменных и целых чисел, это произойдет только в ситуации 1 . В остальных случаях будет истина.
Excel. Функции ЕСЛИ; И; ИЛИ +Примеры использования
Самый практичный совет по записи логических уравнений в программе — не стесняйтесь использовать скобки, если используете математические операторы.
- простое логическое уравнение только из конъюнкции, дизъюнкции и инверсии в лишних скобках не нуждается (кроме тех, конечно, что уже есть в уравнении):
- при появлении импликации и эквиваленции подключаем скобки, чтобы сохранить приоритет и этих, и других логических операторов:
Решение практических задач
Между программированием и алгеброй логики установлен довольно приятный союз:
Например, очень популярная задача алгебры логики — построение таблицы истинности. Давайте попробуем предположить, что нам может понадобиться, чтобы программа смогла это сделать?
А много нам и не надо:
- Нужен перебор логических переменных по совсем небольшому диапазону — от 0 до 1.
- Правильно записанное логическое уравнение, чтобы проверить его при каждом наборе истины и лжи.
Вопрос встает только о конкретной реализации. Python — очень гибкий язык. Для разных формулировок задачи он может предложить разные инструменты, при использовании которых написание кода станет еще приятнее.
Начнем с обобщенной задачи — построение таблицы истинности. На этом примере можно показать, что математические операторы путают приоритет логических. Так что давайте составим таблицу истинности для уравнения A ≡ B ∧ C ⇒ A.
Перебор устроим с помощью вложенных циклов for. Они будут перебирать отдельные переменные, которые потом будут поставляться в логическое уравнение. Для удобства будем сохранять значение уравнения в отдельную переменную, затем выводить все на экран.
print(«A B C») for A in range(0, 2): for B in range(0, 2): for C in range(0, 2): result = A == ((B and C)
Логические выражения и операции. Булевый тип данных
Для того, чтобы программа была не линейной (т.е. в зависимости от ситуации выполнялись разные инструкции) в языках программирования используются логические выражения, результат которых может быть либо правдой ( true ), либо ложью ( false ). Результат логических выражений обычно используют для определения пути выполнения программы.
Проверка условий и логические функции в Excel
Простые логические выражения являются результатом операций отношения между двумя операндами (значениями). В примерах ниже операндами являются значения переменных x и y . Операндами могут быть числа, символы и другие типы данных. Все что можно сравнивать между собой. Однако не рекомендуют сравнивать вещественные числа из-за особенностей их хранения в памяти компьютера.
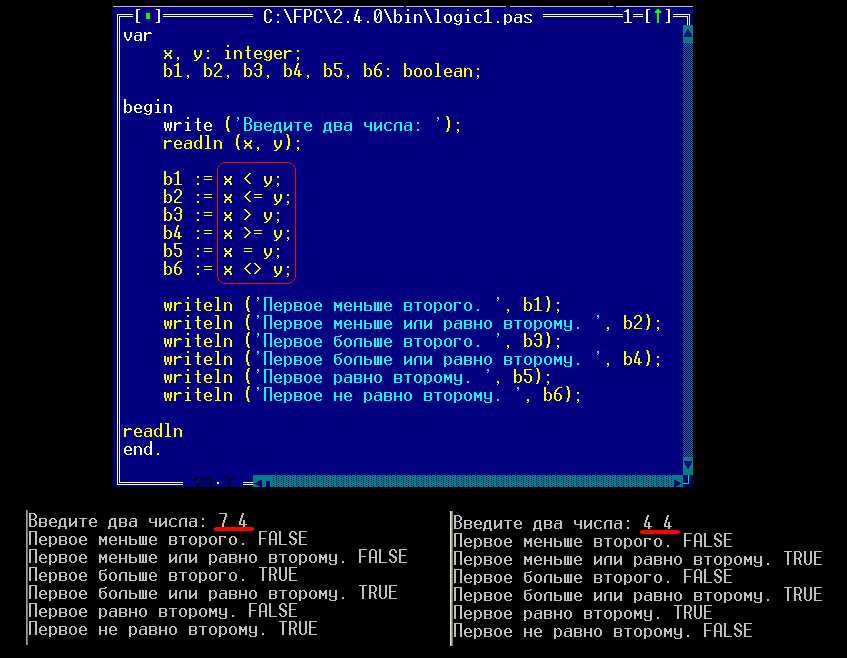
В Паскале предусмотрены следующие операторы отношений:
- меньше: x < y
- больше: x > y
- равно: x = y
- не равно: x <> y
- меньше или равно: x
- больше или равно: x >= y
Булевы типы
Результатом логического выражения всегда является булево (логическое) значение. Булев тип данных ( boolean ) может принимать только два значения: true (истина) или false (ложь). Эти величины упорядочены следующим образом: false < true .
var x, y: boolean; begin x := true; y := false; writeln(‘x = ‘, x); writeln(‘y = ‘, y); writeln(‘x < y = ‘, x < y); end.
x = TRUE y = FALSE x < y = FALSE
Операции and , or , not (применяемые к булевским операндам) дают булевские значения.
Это значит, что данные булевого типа являются не только результатом операций отношения, но и могут выступать в роли операндов операции отношения. Также к ним можно применять функции ord , succ , pred , процедуры inc и dec .
Значение типа boolean занимает в памяти 1 байт.
В примере шести булевым переменным присваиваются значения простых логических выражений. Значения, хранимые в таких переменных, затем выводятся на экран.
Кроме типа boolean в Pascal введены еще три булевых типа — bytebool (занимает 1 байт), wordbool (занимает 2 байта) и longbool (занимает 4 байта).
Для всех булевых типов значению false соответствует 0, а значению true — любое ненулевое значение. Логические переменные, принадлежащие разным булевым типам, ведут себя по-разному при выполнении над ними операций. Ниже приводится пример, реализованный на языке FreePascal (в комментариях отображается результат).
var b:boolean; wb:wordbool; begin b:= false; b:= pred(b); writeln(b,’ ‘,ord(b)); // TRUE 255 writeln(b=true); // TRUE wb:= false; wb:= pred(wb); writeln(wb,’ ‘,ord(wb)); // TRUE -1 b:= true; b:= succ(b); writeln(b,’ ‘,ord(b)); // TRUE 2 wb:= true; wb:= succ(wb); writeln(wb,’ ‘,ord(wb)); // FALSE 0 end.
Логические операции
С помощью логических операторов можно формировать сложные логические выражения. Логические операторы часто применяются по отношению к простым логическим выражениям.
В языке программирования Pascal предусмотрены следующие логические операции:
-
Конъюнкция (логическое умножение, пересечение) — and . Выражение a and b дает значение true только в том случае, если a и b имеют значение true . Во всех остальных случаях значения выражения a and b дает false .
true and true = true true and false = false false and true = false false and false = false
true or true = true true or false = true false or true = true false or false = false
not true = false not false = true
true xor true = false true xor false = true false xor true = true false xor false = false
Последовательность выполнения логических операторов: not, and, or.
В языке Паскаль сначала выполняются логические операторы ( and , or , xor , not ), а уже потом операторы отношений ( > , >= , < , , = ), поэтому не нужно забывать расставлять скобки в сложных логических выражениях.
Сложные булевы выражения могут не обрабатываться до конца, если продолжение вычислений не изменит результат. Если булево выражение в обязательном порядке нужно обрабатывать до конца, то это обеспечивается включением директивы компиляции .
Стандартные функции, возвращающие булевые значения
- odd(x) = true, если x нечетный ( x целый);
- eoln(x) = true, если встретился конец строки текстового файла x ;
- eof(x) = true, если встретился конец файла x .
В остальных случаях эти функции принимают значение false .
Источник: pas1.ru
Логические выражения в C++ — урок 5

Всем привет! Сейчас пойдет о логических операторах в C++. Поскольку нам постоянно надо что-то сравнивать (например что больше, а что меньше), то нам надо иметь возможность реализовывать подобный функционал и в C++.
Логические переменные
Для того, чтобы мы могли хранить данные логического типа, нам надо знать о логических переменных. Мы уже встречались и ими в нашем прошлом уроке. Но давайте повторим:
- Логические данные хранятся в переменных типа bool.
- Хранить они могут только два значения:
- «Верно» — это true ;
- «Лож» — это false ;
Теперь давайте узнаем какие логические операторы существуют в C++.
Операторы сравнения
Язык C++ имеет 5 различных операторов сравнения в своем арсенале. Также существуют такие операторы, которые являются комбинациями других. Все они вам должны быть знакомы из курса математики, поэтому их изучение не должно вызвать у вас проблем.
Давайте разберем по порядку каждый из них:
- A < B — сравнивает две переменные и возвращает true, если A меньше B.
- A > B — возвращает true, если A строго больше B.
- A == B — проверяет на равенство переменные A и B.
- A != B — проверяет переменные A и B на неравенство.
- A >= B — нестрогое неравенство. Возвращает true, если A больше или равно B.
- A B.
Теперь давайте разберем пару примеров, тем самым подкрепим теорию практикой:
bool r ; int a = 5 , b = 7 ; // создали переменные с которыми будем работать
r = a > b ; // r содержит false, поскольку 5 < 7
r = a <= b ; // r содержит true
r = a <= 5 // r равен true
r = b == 9 // r содержит false, поскольку 7 != 9
Из примера видно, что в качестве A и B мы можем использовать не только переменные, но и простые числа.