Линейной называется программа, являющаяся записью линейного алгоритма. В такой программе все операторы выполняются строго последовательно, т.е. после выполнения каждого из них (кроме END) ЭВМ автоматически переходит к выполнению следующего за ним оператора.
Составление простейших программ
Простейшими будем называть линейные программы, не содержащие массивов. Составление таких программ требует знания ранее рассмотренных операторов, понимания их соответствия блокам схемы алгоритма и производится согласно такому несложному правилу:
рассматриваем блоки схемы алгоритма (считаем, что она дана) по порядку, начиная с первого, и для каждого из них записываем соответствующий ему оператор Бейсика, т.е.
для блока Начало — оператор REM с названием программы;
для блока Ввод — оператор ввода;
для блока Процесс — оператор присваивания;
для блока Вывод — оператор вывода;
для блока Останов — оператор END.
В этом все правило!
Теперь приведем примеры конкретных программ рассматриваемого вида.
PascalABC Урок №1 для чайников. Линейная программа.
Вычислить периметр прямоугольного треугольника, если заданы длины его катетов.
Переставить значения величин А и В.
Решение задач 12.2 и 12.3. Эти задачи рассматривались в главе 10, поэтому на рис. 12.2 приведены без пояснений схема алгоритма и программа задачи 10.2, а на рис. 12.3 — то же для задачи 10.3.
На рис. 12.2 и 12.3 стрелками показано соответствие операторов программы блокам схемы алгоритма.
Приведем программы решения еще двух задач. Программа задачи 12.1 иллюстрирует использование величин различного типа. Программа задачи 12.2 демонстрирует организацию вывода данных на печатающее устройство.


Рис. 12.2 Рис. 12.3
Вычислить значения У и Z по формулам:

где В и В — целые величины.
Исходные данные: Э%, В%, С, X, А(а).
Результат: Y,Z%.
Порядок выполнения операций здесь очевиден, поэтому сразу напишем программу:
- 10 REM ЗАДАЧА 1
- 20 PRINT «ВВЕСТИ D%, В%, С, X, А»
- 30 INPUT D%,В%, С, X, А 40 R$=»HBAH0B, 10А КЛ»
- 50 Z%=2*D%—3*В%
- 60 Y=(3*ABS(X)+С:(1/3)+SIN(A)/COS(А))*Z%
- 70 PRINT «Z%=»;Z%; «Y advconts adv3»>
- 20 REM ВЫВОД НА ПЕЧАТЬ 30 PRINT «ВВЕСТИ А, В»
- 40 INPUT А, В 50 У=А Л 2+В Л 2
- 60 LPRINT «ДАННЫЕ:»,» А=»;А;» В РЕЗУЛЬТАТ:»,» Y /htm/img/4/10236/324.png» width=»273″ height=»92″ decoding=»async» loading=»lazy»/> т.е. содержат три строки и четыре столбца. Составление линейных программ с массивами. Прежде всего отметим особенности работы с массивами в программе. 1. Элементы массивов получают значения с помощью операторов ввода или присваивания как простые переменные. При вводе (выводе) массивов в операторах ввода (вывода) перечисляются имена всех вводимых (выводимых) элементов массива. Пример: программа ввода и вывода массива Р (1:3) может иметь такой вид:
- 20 DIM Р(3)
- 30 INPUT Р(1), Р(2), Р (3)
- 40 PRINT Р(1), Р(2), Р(3)
- 50 END
- 2. Все массивы можно разделить на два вида:
- • массивы постоянного размера (например, Р( 1:7), В(1:4, 1:8)];
- • массивы переменного размера [например, А(1: С(1 :т, 1: d). В главах 8 и 9 мы использовали оба вида, не делая различий между ними.
В некоторых версиях Бейсика оператор DIM не позволяет объявлять массивы переменного размера, поэтому использование их в программе требует некоторых ухищрений. В версиях Бейсика, рассматриваемых в пособии, таких ограничений нет, допустимо использовать массивы любого вида.
C++ | Линейный алгоритм в С++ (А + В)
Следует только помнить: переменные — размеры массивов должны быть определены до обращения к оператору DIM.
10 INPUT М 20 DIM Х(М)
Линейные программы с массивами составляются в соответствии с рассмотренным ранее правилом составления простейших программ, которое можно дополнить одним пунктом — «после оператора REM следует записать в программе оператор DIM». Кроме того, необходимо учитывать только что изложенные сведения о работе с массивами.
Теперь покажем построение рассматриваемых программ на конкретных примерах. Для начала вернемся к задаче 8.5. Схема алгоритма ее приведена на рис. 10.11. Заменив каждый блок этой схемы соответствующим оператором согласно правилу, приведенному в 12.2, и добавив оператор DIM, получим программу, приведенную ниже. После ознакомления с этой программой рекомендуем читателю самому составить программу решения задачи 10.7 и сравнить ее с приведенной ниже:
- 10 REM СУММА
- 20 DIM В(3, 3), S (2)
- 30 PRINT «ВВЕСТИ МАТР. В(3, 3)»
- 4 0 INPUT В(1, 1), В(1, 2), В(1, 3)
- 50 INPUT В (2, 1), В (2, 2), В(2, 3)
- 60 INPUT В(3, 1), В(3, 2), В(3, 3)
- 70 S(l) =В (1, 1)+В(1, 2 ) +В (1, 3)
- 80 S (2) =В (1, 3) +В (2, 3)+В(3, 3)
- 90 PRINT «S(1)=»; S (1); «S(2) ВВЕСТИ МАССИВ В (4) «
- 40 INPUT В(1), В(2),
- 50 D=B(1)
- 60 В(1)=В(2)
- 70 В(2)=В(3)
- 80 В(3)=В (4)
- 90 В(4)=D
- 100 PRINT «МАССИВ В=(«;
- 110 PRINT В(1); В(2);
- 1. Какой оператор в Бейсике указывает тип и размеры массива?
- 2. Каково обозначение элементов массива в Бейсике? Каково наименьшее значение индекса элемента массива?
Задачи для самостоятельного решения

В приведенных далее задачах составить схему алгоритма и программу. 1. Вычислить
- 2. Вычислить среднее арифметическое переменных В, Си И.
- 3. Рабочие Иванов и Петров изготовили за смену А и В деталей соответственно, перевыполнив норму. Определить процент перевыполнения нормы (норма — С деталей в смену).
- 4. Определить разницу в возрасте невест для двух братьев Пети и Димы. Их возраст а и Ь соответственно. Возраст невесты определяется по формуле

где (7 — возраст жениха.
5. Вычислить значение у:


где

Примем кф 0; г,Ф 0.
- 6. Вычислить объем и площадь поверхности цилиндра диаметром О и высотой Н.
- 7. Вычислить стоимость мебельного гарнитура, содержащего четыре стула, два кресла и один стол. Стоимость изделий соответственно А, В и С руб.
- 8. Определить среднее арифметическое элементов массива С(1:5).
- 9. Определить произведение сумм элементов каждой строки матрицы Р(1:2, 1:3).
- 10. Переставить соответствующие элементы первой и второй строк матрицы А( 1:2, 1:2).
- 11. Переставить элементы массива Я(1: 6): 1-й элемент и 6-й, 2-й и 5-й, 3-й и 4-й.
Источник: bstudy.net
2. Линейное программирование на Python. Практическая реализация
В этом руководстве мы будем использовать для решения описанной выше задачи линейного программирования два пакета Python :
- SciPy – универсальный пакет для научных вычислений с Python. Его внутренний пакет scipy.optimize можно использовать как для линейной, так и для нелинейной оптимизации.
- PuLP – API линейного программирования Python для определения задачи и вызова солверов. По умолчанию в качестве солвера используется COIN-OR Branch and Cut Solver (CBC). Еще один отличный солвер с открытым исходным кодом – GNU Linear Programming Kit (GLPK).
2.1. Установка SciPy и PuLP
Чтобы следовать этому руководству, вам необходимо установить SciPy и PuLP.
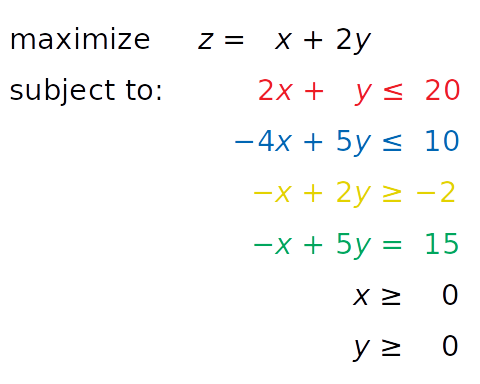
linprog() решает только задачи минимизации (не максимизации) и не допускает ограничений-неравенств со знаком больше или равно ( ≥ ). Чтобы обойти эти проблемы, нам необходимо изменить описание задачи перед запуском оптимизации:
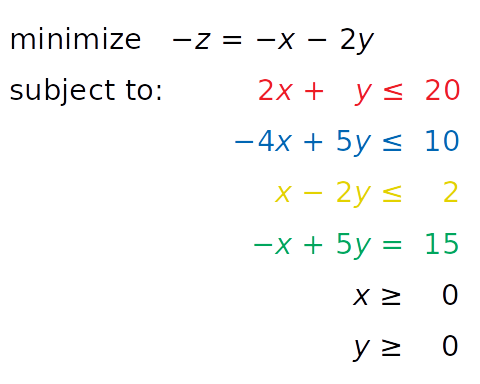
- Вместо максимизации z = x + 2y минимизируем отрицательное значение ( −z = −x − 2y ).
- Вместо знака ≥ мы можем умножить «желтое» неравенство на -1 и получить противоположный знак (ограничения по осям рассмотрим далее).
На следующем шаге определяем входные значения:
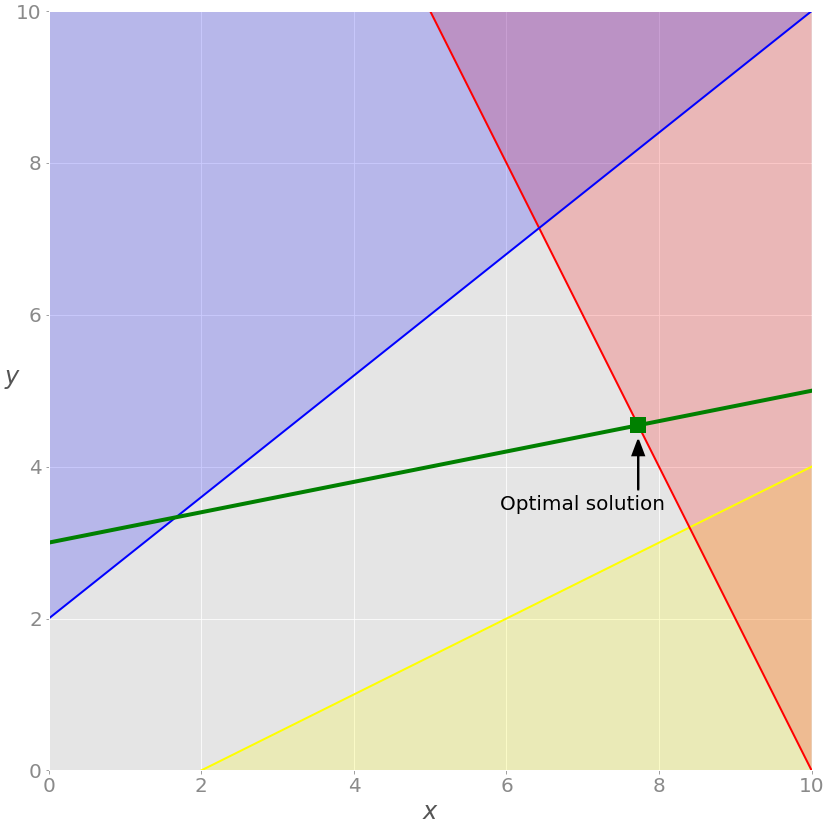
Вначале наша задача органичивалась только неравенствами. Если удалить параметры зеленого уравнения A_eq и b_eq из вызова linprog() , получим следующий результат:
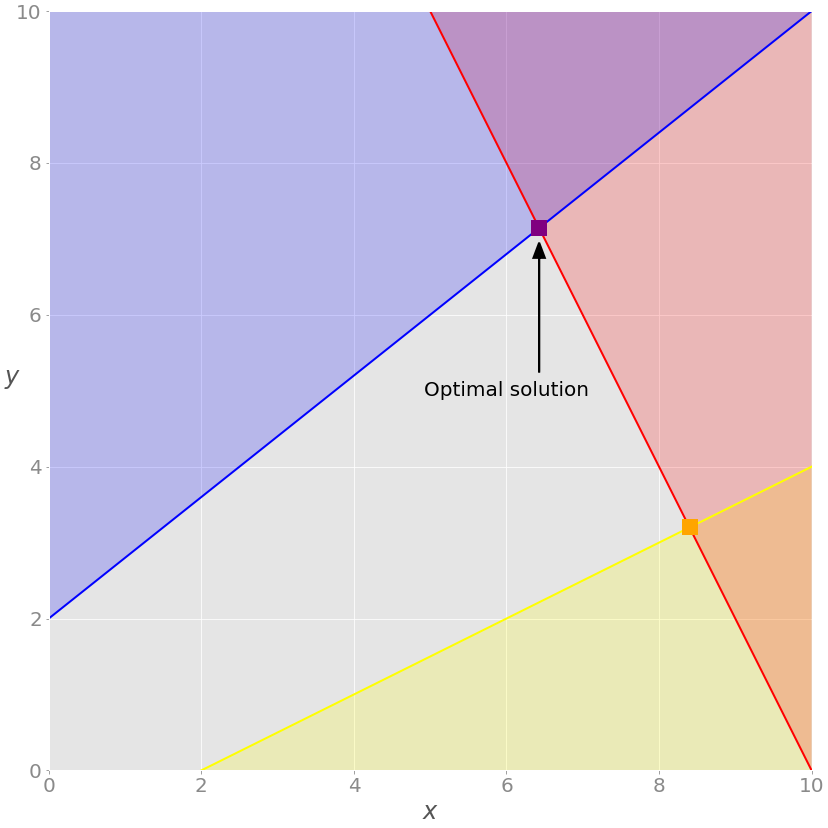
2.4. Решение задачи о производстве с помощью SciPy
Рассмотрим теперь решение второй задачи – о продуктах, рабочей силе и используемом сырье.
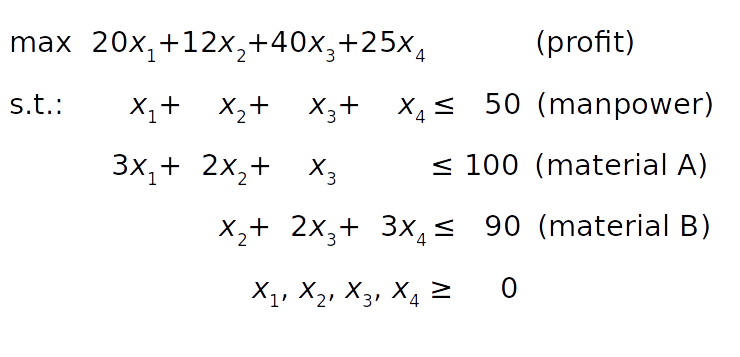
Как и в предыдущем примере, нам нужно извлечь необходимые векторы и матрицу из задачи, передать их в качестве аргументов в linprog() :
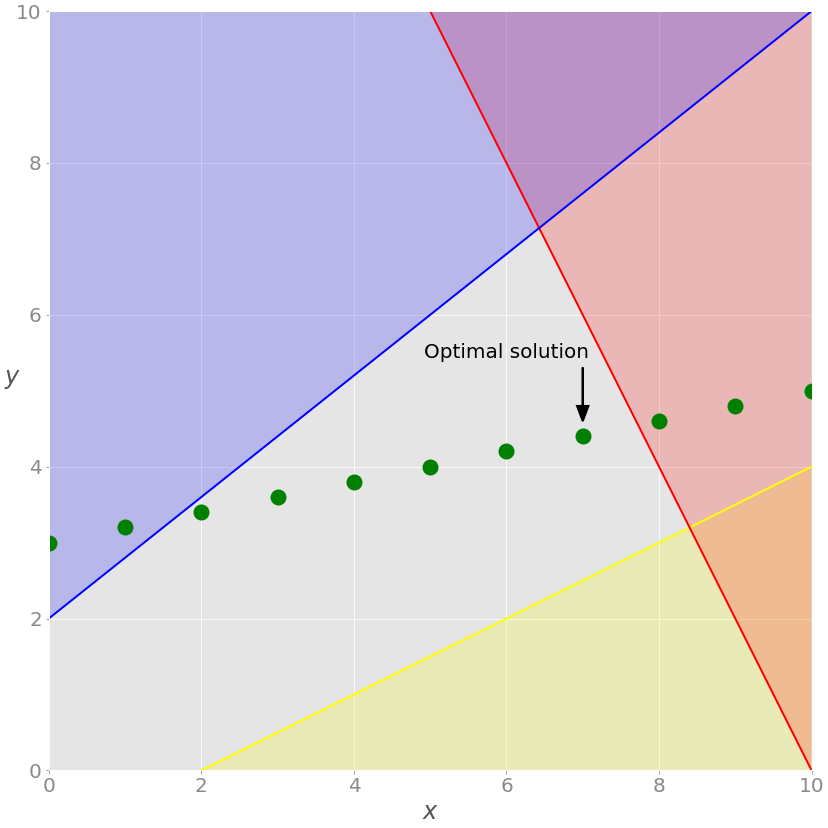
Как видите, оптимальным решением является крайняя правая зеленая точка на сером фоне. Это решение с наибольшими значениями как x , так и y , дающее максимальное значение целевой функции.
2.6. Решение задачи о производстве с помощью PuLP
Подход к определению и решению второй задачи такой же, как и в предыдущем примере:
# Определяем модель model = LpProblem(name=»resource-allocation», sense=LpMaximize) # Описываем переменные x = «, lowBound=0) for i in range(1, 5)> # Добавляем ограничения model += (lpSum(x.values()) , «) print(f»objective: «) for var in x.values(): print(f»: «) for name, constraint in model.constraints.items(): print(f»: «)
status: 1, Optimal objective: 1900.0 x1: 5.0 x2: 0.0 x3: 45.0 x4: 0.0 manpower: 0.0 material_a: -40.0 material_b: 0.0
Как видите, решение согласуется с тем, что мы молучили с помощью SciPy. Наиболее выгодное решение – производить в день 5 единиц первого продукта и 45 единиц третьего.
Давайте сделаем задачу более интересной. Допустим, из-за проблем с оборудованием, фабрика не может производить первую и третью продукцию параллельно. Какое решение наиболее выгодно в этом случае?
Теперь у нас есть еще одно логическое ограничение: если x_1 положительно, то x_3 должно равняться нулю, и наоборот. Здесь пригодятся бинарные переменные решения. Введем две переменные y_1 и y_3 , которые будут обозначать, генерируются ли вообще первый или третий продукты:
model = LpProblem(name=»resource-allocation», sense=LpMaximize) x = «, lowBound=0) for i in range(1, 5)> y = «, cat=»Binary») for i in (1, 3)> model += (lpSum(x.values()) , «) print(f»objective: «) for var in model.variables(): print(f»: «) for name, constraint in model.constraints.items(): print(f»: «)
status: 1, Optimal objective: 1800.0 x1: 0.0 x2: 0.0 x3: 45.0 x4: 0.0 y1: 0.0 y3: 1.0 manpower: -5.0 material_a: -55.0 material_b: 0.0 x1_constraint: 0.0 x3_constraint: -55.0 y_constraint: 0.0
При таких условиях оказывается, что оптимальный подход – исключить первый продукт вовсе и производить только третий.
Заключение
Теперь вы в общих чертах представляете, с какими задачами имеет дело линейное программирование и как использовать Python для решения подобных задач.
Теперь – после прохождения этого руководства – вы умеете:
- определить модель, которая описывает задачу в SciPy и PuLP;
- создать программу Python для оптимизационной задачи;
- запустить программу оптимизации, чтобы найти решение задачи;
- получить результат оптимизации.
Если вы хотите узнать больше о линейном программировании, вот несколько отправных точек, с которых можно начать:
- русскоязычная и анлоязычная вики-страницы о линейном программировании;
- русскоязычная и англоязычная вики-страницы о целочисленном программировании;
- туториал на Brilliant.org;
- вводный курс MIT о математическом программировании.
Следите за нашими тегами Python и Математика!
Больше полезной информации вы можете получить на нашем телеграм-канале «Библиотека питониста». Рекомендуем также обратить внимание на учебный курс по Python от «Библиотеки программиста».
Источники
Источник: proglib.io