2) Функциональная – соответствие функций комплекса функциям спецификации.
Эталоны и методы проверки корректности
Средства проверки корректности
Способы формирования эталонных тестов
1) Применение аналитических выражений
2) Использование моделирования
3) Использование прежних вариантов тестирования подобных программ
Понятие верификации программы
Верификация – аналитическое исследование корректности программы по ее тексту на основе формально-логической системы установления соответствия между программой и ее спецификацией с помощью аппарата исчисления предикатов первого порядка. В конечном счете это вычисление истинности предиката от двух аргументов: программы и ее спецификации.
Для упрощения верификации разделяют две составляющих выполнения программы:
1) частичную корректность – удовлетворение входной и выходной спецификациям программы при условии ее успешно завершения
2) проверка завершенности программы – достижение выхода при заданных спецификацией входных данных
02 Проверка гипотез Лекция
Основные задачи анализа корректности при верификации
1) частичная корректность при условии завершенности
2) частичная некорректность при условии завершенности
5) тотальная корректность – частичная корректность и завершенность
6) некорректность – частичная некорректность или незавершенность
| START P(x) | Выходу оператора приписывают предусловие P(x), это допустимое множество значений входных данных |
| STOP Q(x, f(x)) | Оператор, обеспечивающий завершение, входу которого приписывается выходной предикат, или постусловие, где f(x) – целевая функция выполнения программы (которая устанавливает связь между входными и выходными данными) |
| Pgrm | Спецификация, которая задает набор индуктивных объявлений для каждой точки графа разреза управления |
1) Свойство частичной корректности
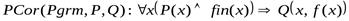
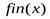
— предикат завершенности программы
2) Свойство завершенности
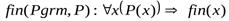
3) Тотальная корректность
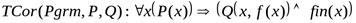
Есть ограничения на форму представления программ и операторов, для которых вычисляются предикаты.
Проверка 6 свойств корректности программ с определенными ограничениями осуществляется методом индуктивных утверждений, предложенных Флойдом.
https://studfiles.net
https://works.doklad.ru/view/7bOqlofhMVE.html
http://www.tadviser.ru
https://studopedia.org
На этом занятии мы познакомились с основными этапами решения задач с помощью компьютера.
Основные этапы решения задачи на ПК:
Просто о сложном, сложно о простом. Что такое корректность программ. Вадим Винник
— Нужно понять и отнести к какому классу принадлежит задача;
— Записать известные связи между исходными данными и результатами с помощью математических соотношений;
— Выбрать подходящий способ решения задачи;
— Построить алгоритм для решения задачи;
— Записать код, на основе алгоритма, на одном из языков программирования;
— Отладка и тестирование программы.
Дата добавления: 2018-11-24 ; просмотров: 335 ; Мы поможем в написании вашей работы!
Поделиться с друзьями:
Источник: studopedia.net
II. Эталоны и методы проверки корректности.
Эталоны для проверки корректности программ могут использоваться в следующих трех формах, поясняемых с помощью рис.13:
1. Формализованные правила.
2. Программные спецификации.
Формализованные правила — имеют достаточно неопределенностей, так как опреде-ляются двумя видами требований
требования стандартов (общероссийских и стандартов предприятий)
требования языков и технологий программирования.



контроль полноты спецификаций
Статическое и динамическое тестирование
Для полной убедительности в корректности программ одних формализованных правил недостаточно.
2. Программные спецификации — относятся к функциональным эталонам и в основ-ном обеспечивают проверку корректности программ в статике.
В зависимости от стадии и характера проверки разделяются тесты делятся на статические и динамические. Статическое тестирование — ручное тестирование программ, начиная со стадии формирования требований к программе. На стадии кодирования при статическом тестировании некоторую часть маршрутов исполнения тестируют вручную. Динамическое тестирование подразумевает достаточно полную структурную и функциональную проверку выполнения программы.
Как формируются эталоны для тестирования? Существует несколько способов формирования эталонов:
Использование аналитических выражений. Этот способ особенно подходит при детерминированном тестировании, так как имеется возможность сравнить результаты тестирования с ожидаемыми результатами. Имеются ограничения в использовании этого метода, если неизвестны или отсутствуют аналитические выражения связывающие входные данные и результаты; иногда требуется использовать много допущений.
Использование моделирования на ЭВМ. Способ является универсальным. При этом ряд данных моделируется другим способом и по другим алгоритмам, нежели испытываемая программа и на других ЭВМ. Причем наборы входных данных создаются по случайным законам, что обеспечивает высокую гибкость этого способа.
Использование результатов испытаний предшествующих вариантов программ.
При этом используется ранее накопленный опыт испытателя или других исследователей, выраженный в экспертных оценках ожидаемых результатов.
Степень достоверности проверки корректности программ при использовании этих методов убывает по номерам способов формирования эталонов.
В 1-ом случае обеспечивается 100% гарантия корректности программ, в третьем случае такой уверенности нет, но мы можем убедиться в том, что программа работает так же или иначе, чем аналогичный вариант. Менее достоверные тесты приходится использовать из-за недостаточности сил и средств.
Лекция 9. Аналитическая проверка корректности программ. Верификация программ.
Корректность является статическим свойством программы, поскольку она не зависит от времени (если, конечно, не изменяются цели разработки) и отражает специфику ошибок разработки программ (ошибок проекта и кодирования).
Различают два типа проверки корректности:
валидация (validation) – установление соответствия между тем, что делает программа, и тем, что нужно Заказчику;
верификация (verification) – установление соответствия между программой и ее спецификацией.
Определение верификациии симметрично ввиду относительного характера свойства корректности: если программа не соответствует своей спецификации, то либо программа, либо спецификация, либо оба этих объекта содержат ошибки. Перефразируя известное изречение Э.Дейкстры о тестировании программ, можно сказать, что верификация способна доказать отсутствие ошибок в программе, но не всегда доказывает их присутствие.
В отличие от тестирования верификация предполагает аналитическое исследование свойств программы по ее тексту (без выполнения программы). Таким образом, для проведения верификации необходимо построить формально-логическую систему, в которой были бы формально определены свойства корректности программы. Для этих целей наиболее широкое применение получило исчисление предикатов первого порядка, расширенное аксиоматической арифметикой.
Можно сказать, что верификация – это вычисление истинности предиката от двух аргументов: программы и спецификации. Истинность этого предиката устанавливает свойство корректности программы, если спецификация не содержит ошибок, однако, его ложность, вообще говоря, не означает наличие ошибок в программе, а требует более точного разбора.
Учитывая специфику проявления ошибок в программах в процессе их выполнения на ЭВМ, целесообразно выделить в понятие корректности программы два свойства:
частичную корректность – удовлетворение внешним (входной и выходной) спецификациям программы при условии завершения выполнения программы;
завершенность – достижение в процессе выполнения выхода программы при определенных входной спецификацией данных.
Свойство завершенности не является тривиальным для такого объекта, как программа, ввиду возможности циклических и рекурсивных вычислений, а также наличия частично-определенных операций. Случаи, когда свойство завершенности не удовлетворяется, довольно обычны для программ с ошибками, и приводят к заведомо некорректным программам независимо от спецификации выхода.
Каждое из двух выделенных свойств корректности программы может удовлетворяться или не удовлетворяться. Таким образом, можно выделить шесть основных задач анализа корректности программы:
частичная корректность (при условии завершенности);
тотальная корректность (частичная корректность и завершенность);
частичная некорректность (некорректность при условии завершенности);
некорректность (незавершенность или частичная некорректность).
Разделение свойств частичной корректности и завершенности следует рассматривать как методологический прием, направленный на уменьшение сложности верификации программ.
Рассмотрим формальные постановки задач анализа корректности.
Введем ограничение: будем рассматривать программы, начинающиеся оператором START (первый выполняемый оператор) и заканчивающиеся оператором STOP (последний выполняемый оператор).
Спецификацию программы Prgm будем определять путем приписывания индуктивных утверждений точкам разреза графа потоков управления программы (точкам между операторами программы). При этом выходу оператора START приписывается входной предикат (предусловие) программы P(x), определяющий множество допустимых значений исходных данных x (x допустимо, если P(x): true), а входу оператора STOP приписывается выходной предикат (постусловие) Q(x,y), определяющий целевую функцию программы (связь между входными и выходными данными программы).
Тогда свойство частичной корректности программы определяется следующей формулой логики предикатов:
PCOR(Prgm, P, Q): x ( P(x) fin(x) Q( x, f(x) ) ),
где fin(x) – предикат завершения программы Prgm, начатой в состоянии x;
f(x) – функция, вычисляемая программой Prgm,
свойство завершенности может быть определено формулой:
FIN(Prgm, P): x ( P(x) fin(x) ),
а свойство тотальной корректности формально выражается как одновременное присутствие свойств частичной корректности и завершенности:
TCOR(Prgm, P, Q): x ( P(x) Q(x, f(x) ) fin(x) ).
Аналогичным образом могут быть формализованы и другие перечисленные выше свойства корректности (записать самостоятельно).
Заметим, что для произвольных программ каждое из этих свойств (завершенность и частичная корректность) является алгоритмически неразрешимым, т.е. не существует алгоритма, позволяющего оценить истинность соответствующих формул логики предикатов. Однако для отдельных классов программ в настоящее время разработаны достаточно эффективные методы верификации, позволяющие вручную или автоматически проводить соответствующие доказательства. Такие методы могут рассматриваться как составная часть процессов разработки и отладки программ, обеспечивая логическую завершенность этих процессов.
Наиболее распространенным методом доказательства частичной корректности программ является метод индуктивных утверждений, предложенный Флойдом. Он позволяет свести доказательство частичной корректности программы к доказательству некоторого конечного числа утверждений, записанных на языке исчислений предикатов первого порядка и имеющих интерпретацию в соответствующей проблемной области.
Рассмотрим метод индуктивных утверждений для программ с конечным множеством простых переменных < x1, x2, … xn >, где n1, а операторами являются:
операторы присваивания вида xi := f (x1, x2, … xn);
составной оператор вида A ; B ;
оператор условного перехода if (x1, x2, … xn) then L+ else L– ,
где L+, L– – метки операторов, которым передается управление;
начальный оператор START;
конечный оператор STOP.
Такой состав структурных компонентов вполне достаточен для представления произвольного алгоритма и поэтому не ограничивает общности излагаемого метода.
Установление частичной корректности осуществляется за четыре последовательных шага.
Шаг 1. Разрезание циклов программы
Очевидно, что при выполнении программы для различных исходных данных возможны различные последовательности операторов, начинающиеся оператором START и оканчивающиеся оператором STOP. Назовем такие последовательности трассами вычислений.
Сложность анализа частичной корректности программы разбиением на трассы заключается в том, что при наличии циклов в программе он не может быть выполнен непосредственным перебором всех трасс. Эта сложность может быть преодолена путем включения в граф потока управления программы конечного числа точек, называемых точками разреза, таким образом, что каждый цикл содержит одну такую точку, которая “разрезает” циклические пути на два:
путь через тело цикла;
путь к выходу из цикла.
Шаг 2. Получение аннотированной программы
С каждой точкой разреза k свяжем предикат
Источник: studfile.net
Основные виды корректности комплексов программ

56. Надежность программных средств. Показатели надежности ПС. Факторы, определяющие надежность ПС.
Надежность программного обеспечения — свойство программы выполнять заданные функции, сохранять свои характеристики в установленных пределах при определенных условиях эксплуатации. Надежность программного обеспечения определяется его безотказностью и восстанавливаемостью.
Безотказность программного обеспечения или программы – свойство программы сохранять работоспособность при использовании в процессе обработки информации. Безотказность программного обеспечения можно оценить вероятностью его работы без отказов при определенных условиях внешней среды в течение заданного периода наблюдения. В данном определении под отказом программного обеспечения понимается недопустимое отклонение характеристик процесса функционирования программы от требуемых. Определенные условия внешней среды понимаются как совокупность входных данных и состояния вычислительной системы. Заданный период наблюдения, как правило, соответствует необходимому для выполнения программы.
Безотказность программного обеспечения можно также характеризовать средним временем между возникновениями отказов в процессе функционирования программы. При этом предполагается, что аппаратура информационной системы находится полностью в работоспособном состоянии.
С точки зрения надежности принципиальное отличие программного обеспечения от аппаратуры состоит в том, что программное обеспечение не изнашивается и его выход из строя из-за поломки невозможен. Поэтому характеристики функционирования программного обеспечения зависят только от его качества.
В значительной степени на функционирование программного обеспечения влияют входные данные. Так проявление ошибок программного обеспечения связано с тем, что в некоторые моменты времени на обработку поступают ранее не встречавшиеся совокупности данных, которые программа не в состоянии корректно обработать.
На рис.1 показана зависимость, отражающая изменение во времени надежности программы.
Рисунок 1. Изменение надежности программы во времени
Увеличение надежности программы является следствием того, что в процессе эксплуатации обнаруживаются и устраняются скрытые ошибки. Правда, при этом могут возникать так называемые ошибки второго рода, связанные с внесением новых ошибок в процессе устранения старых.
Важной характеристикой надежности программного обеспечения является его восстанавливаемость, которая определяется затратами времени и труда на устранение отказа из-за проявившейся ошибки в программе и его последствий. Восстановление после отказа в программе может заключаться в корректировке и восстановлении текста программы, исправлении данных, внесения изменений в организацию вычислительного процесса.
Восстанавливаемость программного обеспечения может быть оценена средней продолжительностью устранения ошибки в программе и восстановления ее работоспособности. Восстанавливаемость программного обеспечения зависит от многих факторов, в том числе от сложности структуры комплекса программ, структурированности самих программ, языка программирования, на котором разрабатывалась программа, стиля программирования, качества документации на программу и т.д.
Можно также говорить об устойчивости функционирования программного обеспечения.
Устойчивость функционирования – способность программы ограничивать последствия собственных отказов и неблагоприятных воздействий внешней среды (неисправность аппаратуры, некорректность входных данных, ошибки оператора) или противостоять им.
Устойчивость программного обеспечения может быть повышена с помощью разных форм структурной, информационной и временной избыточности (дублирующие модули программ, альтернативные программы для решения одних и тех же задач, контроль за процессом исполнения программы).
Основными показателями надежности ПО являются:
· вероятность безотказной работы программы p(t), представляющая собой вероятность того, что ошибки программы не проявятся в интервале времени (0, t);
· вероятность отказа программы q(t) или вероятность события отказа ПО до момента времени t;
· интенсивность отказов программы l(t);
· средняя наработка программы на отказ T, являющаяся математическим ожиданием временного интервала между последовательными отказами.
При определении характеристик надежности ПО учитывается тот факт, что возникающие при работе программ ошибки устраняются, количество ошибок уменьшается и, следовательно, их интенсивность понижается, а наработка на отказ программы увеличивается. В связи с такими предположениями рассматривается несколько моделей надежности ПО: модель с дискретно-понижающей частотой появления ошибок, модель с дискретным увеличением наработки на отказ или ошибку ПО, экспоненциальная модель надежности ПО.
Источник: studopedia.info