Комбинаторная программа что это
КОМБИНАТОРНАЯ ЛОГИКА
- Описание
- Алфавитный указатель
- Арабская философия
- Индийская философия
- Китайская философия
- Русская философия
- Этика
- Авторы
- Приложения
КОМБИНАТОРНАЯ ЛОГИКА – направление в основаниях и философии математики, в котором в качестве основных понятий выбираются: функция (оператор) и операция аппликации (application) – применение (приложение) функции f к аргументу g, пишут: (fg). Функции понимаются теоретико-операторно, бестипово, т.е. допустимы: (gf), (gg), (g(ff)), ((gg)(fg)) и т.д.
Выражение вида f(x1, …, xn), является лишь записью для (. ((fx1)x2)..хn). Тем самым многоместные функции сводятся к одноместным. Опуская скобки, пишут: fx1x2 … xn вместо х1, . , хn можно поставить f, получая fff …f.
Здесь n≥0 (если n = 0, то f – нульместная функция).
Исходными объектами (сокращенно, по X.Карри, обами) в комбинаторной логике служат константы и переменные (множество переменных может быть пустым). Новые обы строятся из исходных и полученных ранее по правилу: если a и b – обы, то (ab) считается обом.
Комбинаторные задачи. 5 класс
Выделяются три константы, обозначающие индивидуальные функции (комбинаторы): два собственных комбинатора К и S, удовлетворяющих равенствам Kab = а и Sabc = ac(bc), где a, b и с – произвольные обы (скобки в обах восстанавливаются по ассоциации влево) и один дедуктивный комбинатор U как некоторый аналог формальной импликации или оператора функциональности. Эти три комбинатора позволяют заменить любое предложение логико-математических языков комбинацией (обом) из К, S и U и скобок, откуда и название «комбинаторная логика» (введенное Карри).
Употребление же переменных вообще может быть исключено, что соответствует первоначальному замыслу М.И.Шейнфинкеля, Карри и А.Чёрча. К примеру, если А комбинатор такой, что Аху = x + у, а С комбинатор такой, что Cfxy = fyx [или в более обычных обозначениях: приложение комбинатора А к аргументам х, у дает x + у; приложение комбинатора С к fху) дает f(yx)], то сумму у + x в этом случае можно выразить как САху. Тождество x + у =у + x выражается при этом в виде Аху = САху. И если (как это делается обычно в математике) трактовать тождественное равенство f(x1, . хn) = g(x1 . хn) как другое выражение для f = g (т.е. считать, что функции f и g, относящие обе одни и те же объекты к одним и тем же значениям аргументов, отождествляются нами), то другим выражением для тождества х + у = у + х будет формула А = CA, не содержащая переменных.
Создателем комбинаторной логики (1920) является московский математик Моисей Ильич Шейнфинкель (1887–1942). Он ввел комбинаторы К, S и U, сформулировал и обосновал, используя указанные равенства для К и S, принцип комбинаторной полноты, более общий, чем канторовское неограниченное теоретико-множественное свертывание. Шейнфинкель предложил один из первых способов уточнения интуитивного понятия алгоритма, определив по существу комбинаторные алгоритмы как вариант реализации вычислительной (алгоритмической) части дискретно-комбинаторной программы Лейбница.
Решение комбинаторных задач методом перебора. 6 класс.
Независимо от Шейнфинкеля американские математики Карри и Чёрч получили аналогичные результаты. В их трудах комбинаторные алгоритмы представлены дедуктивно в виде доказуемо непротиворечивых исчислений негильбертовского типа. Таковы, в частности, ламбда-исчисления (λ-исчисления) Чёрча, эквивалентные чистой (без логических законов) комбинаторной логике Шейнфинкеля – Карри.
Исчисления Шейнфинкеля – Чёрча – Карри оказались удачными теориями вычислений. Они дали толчок развитию теории рекурсий, различных видов алгоритмов, а в последнее время и информатики. Известны применения комбинаторной логики в доказательств теории, в семантике языков программирования, алгебре, топологии, теории категорий и др. разделах современного знания.
Бестиповые исчисления Шейнфинкеля – Чёрча – Карри (для краткости: ШЧК) были введены прежде всего в расчете на то, что их дедуктивные расширения станут основаниями математики и других наук. Пытаясь реализовать синтаксически дедуктивный комбинатор U, Карри и Чёрч построили также логико-математические исчисления гильбертовского типа, которые, однако, оказались противоречивыми: парадокс Клини – Россера (1936), парадокс Карри (1941).
Отметим, что в парадоксе Карри из логических средств используются только имшшкативные, а правило modus ponens выступает как единственный логический источник противоречивости (см. Парадокс логический). Поскольку все известные дедуктивные системы гильбертовского типа либо бедны выразительными возможностями, либо противоречивы, обращаются к идее ступенчатых расширений. Ступенчатые системы комбинаторной логики строятся на основе комбинаторных алгоритмов путем последовательных расширений бестиповых непротиворечивых исчислений ШЧК, опираясь на принципы дедуктивной полноты – правила введения операторов (прежде всего логических) в сукцедент (в заключение выводимостей) и в антецедент (в посылки выводимостей).
Такая трактовка выводимостей позволила ограничить иерархии двумя ярусами. Первый – исчисления ШЧК. Второй вводится как расширение первого на базе исчисления секвенций – классической логики предикатов первого порядка, распространенной на обы комбинаторной логики, без постулируемого (в силу известного результата Г.Генцена 1934 г.) правила сечения.
Логические связки и кванторы представляются в виде обов, составленных из символов алфавита комбинаторной логики, являющихся константами первого яруса. Среди всех двухярусных систем выделяется А-система со всеми логическими операторами и оператором λ. Ее правила, объединяют два яруса в формальное исчисление (в соответствии с программой Гильберта; см. Формализм), для которого доказываются теоремы о полноте (в смысле Гёделя, ср. его теоремы 1931 г. о неполноте известных исчислений гильбертовского типа) и непротиворечивости (в классическом секвенциальном смысле). Эти правила суть
где а и b – обы, Г, Θ – наборы обов, → и ⇒ суть символы секвенций 1-го и 2-го ярусов, алгоритмической (вычислительной) и дедуктивной (генценовской) соответственно. Говорят, что об а конвертируется в об b, если секвенция а → b выводима в чистой комбинаторной логике (в исчислении ШЧК).
Все элементы языка множеств теории записываются как обы комбинаторной логики с точностью до конвертируемости. Так, атомарная формула b ε а представляется обом bа, по формуле С и переменной x строится новый терм (новое множество) как об λхС, отражая тем самым исходный принцип Кантора: неограниченное образование новых множеств.
В классе всех выводов A-системы выделяется подкласс M всех выводов, в которых применения правила *, структурных и логических правил 2-го яруса ограничены описанными элементами теории множеств. В основе M лежат два принципа, характеризующие канторовскую («наивную») теорию множеств: неограниченное теоретико-множественное свертывание и классическая логика предикатов 1-го порядка без ограничений, соответствующие двум ярусам A-системы. Класс М выступает как вариант непротиворечивой формализации канторовской теории множеств.
Знаменитый парадокс Рассела (1902) отражается в классе M в виде выводов двух дедуктивных секвенций ⇒D) и ⇒⌉D, где ⌉ – знак отрицания, a D – об: ∃λу.Пλх. = (x ε у)(⌉(х ε x)), представляющий частный случай известной схемы теоретико-множественного свертывания, записанной на языке комбинаторной логики.
1. Логика комбинаторная (Яновская С.Л.).– В кн.: Философская энциклопедия, т. 3. М., 1964;
2. Schönfmkel M. Über die Bausteine der Mathematischen Logik. – «Math. Annalen», 1924, Bd 92;
3. Seldin J.P., Hindley J. R. (eds.). Το Η.Β.Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism. L., 1980;
4. Rezus A. A Bibliography of Lambda-Calculi. Combinatory Logics and Related Topics. Amsterdam, 1982;
5. Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика. М., 1985;
6. Кузичев А.С.Об одной арифметически непротиворечивой λ-теории. – «Zeitschrift für Math. Logik und Grundlagen der Mathematik», 1983, Bd 29, H. 5;
7. Кузичева З.Α., Кузечев А.С. Системы с бесконечной логикой и неограниченным принципом свертывания. К 150-летию со дня рождения Г.Кантора. – В кн.: Бесконечность в математике: философские и исторические аспекты. М., 1997;
8. Кузичев А.С. Вариант формализации канторовской теории множеств. – Доклады Российской Академии наук, 1999, т. 369, № 6;
9. Он же. Решение проблемы Гильберта по Колмогорову. – Там же, 2000, т. 371, № 3.
Источник: iphlib.ru
Комбинаторная программа что это
В комбинаторных алгоритмах часто необходимо порождать и исследовать все элементы некоторого класса комбинаторных объектов. Наиболее общие методы решения таких задач основываются на поиске с возвращением, однако во многих случаях объекты настолько просты, что целесообразнее применять специализированные методы. Задачи, требующие генерации комбинаторных объектов, возникают при вычислении комбинаторных формул. Например, часто приходится вычислять суммы, имеющие вид
где суммирование выполняется по всем последовательностям удовлетворяющим некоторым ограничениям.
В алгоритмах порождения комбинаторных объектов нас прежде всего будет интересовать сложность алгоритмов, т.е. общее количество времени, требующегося для порождения всего множества объектов.
4.1. Поиск с возвращением
Использование компьютера для ответа на такие вопросы, как «сколько существует способов. », «перечислите все возможные. », или «есть ли способ. », обычно требует исчерпывающего поиска множества решений. Метод поиска с возвращением постоянно пытается расширить частичное решение. Если расширение текущего частичного решения невозможно, то возвращаются к более короткому частичному решению и пытаются снова его продолжить.
Идею поиска с возвращением легче всего понять в связи с задачей прохода через лабиринт: цель — попасть из некоторого заданного квадрата в другой заданный квадрат путем
последовательного перемещения по квадратам. Трудность состоит в том, что существующие преграды запрещают некоторые перемещения. Один из способов прохода через лабиринт — это двигаться из начального квадрата в соответствии с двумя правилами:
• в каждом квадрате выбирать еще не исследованный путь;
• если из исследуемого в данный момент квадрата не ведут неисследованные пути, то нужно вернуться на один квадрат назад по последнему пройденному пути, по которому пришли в данный квадрат.
Первое правило говорит о том, как расширить исследуемый путь, если это возможно, а второе правило — о том, как выходить из тупика. В этом и состоит сущность поиска с возвращением: продолжать расширение исследуемого решения до тех пор, пока это возможно, и когда решение нельзя расширить, возвращаться по нему и пытаться сделать другой выбор на самом близком шаге, где имеется такая возможность.
Общий алгоритм
В самом общем случае полагаем, что решение задачи состоит из вектора конечной, но неопределенной длины, удовлетворяющего некоторым ограничениям. Каждое где конечное линейно упорядоченное множество. Таким образом, при исчерпывающем поиске должны рассматриваться элементы множества для в качестве возможных решений. В качестве исходного частичного решения примем пустой вектор и на основании имеющихся ограничений выясним, какие элементы из являются кандидатами в Обозначим это подмножество кандидатов через . В результате имеем частичное решение . В общем случае для расширения частичного решения от до кандидаты на роль выбираются из Если частичное решение не представляет возможности для выбора элемента то возвращаемся и выбираем новый элемент Если новый элемент выбрать нельзя, возвращаемся еще дальше и выбираем новый элемент и т.д. Этот процесс удобно представлять в терминах прохождения дерева поиска в
глубину. Процедура поиска с возвращением для нахождения всех решений формально представлена в алгоритме 4.1.
Алгоритм 4.1. Общий алгоритм поиска с возвращениями
Поиск с возвращением приводит к алгоритмам экспоненциальной сложности, так как из предположения, что все решения имеют длину не более исследованию подлежат приблизительно элементов. В предположении, что все константы, получаем экспоненциальную сложность Нужно помнить, что поиск с возвращением представляет собой только общий метод. Непосредственное его применение обычно ведет к алгоритмам, время работы которых недопустимо велико. Поэтому, чтобы метод был полезен, к нему нужно относиться как к схеме, с которой следует подходить к задаче. Схема должна быть хорошо приспособлена (часто это требует большой изобретательности) к конкретной задаче, так чтобы в результате алгоритм годился для практического использования.
Источник: scask.ru
Комбинаторная программа что это
Изучение вероятностно-статистического материала продиктовано самой жизнью. Теория вероятностей в средней школе – это признание обществом необходимости формирования современного мировоззрения.
Необходимость формирования вероятностного мышления обусловлена и тем, что вероятностные закономерности универсальны: физика, химия, биология, математика, весь комплекс социально-экономических наук развивается на базе вероятностно-статистической математики. В соответствии с Федеральными государственными образовательными стандартами в программу по математике за курс основной (средней) школы включаются элементы комбинаторики, статистики и теории вероятностей. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий. В связи с чем, настоящая статья посвящена обучению учащихся решению комбинаторных задач.
теория вероятностей
комбинаторика
размещение
перестановки
1. Андронов А.М., Копытов Е.А., Гринглаз Л.Я. Теория вероятностей и математическая статистика: Учебник для вузов. – СПб.: Питер, 2004. – 461 с.
2. Бунимович Е.А., Булычев В.А. Вероятность и статистика. 5-9 кл.: пособие для общеобразоват. учреждений. – 3-е изд., стереотип. – М.: Дрофа, 2009. – 159 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 6-е, доп. – М.: Высш. шк., 2008. – 405 с.
4. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – 2-е изд., — М.: ЮНИТИ-ДАНА, 2004. – 573 с.
5. Матылыцкий М.А. Теория вероятностей в примерах и задачах: Учеб. пособие. – Гродно: ГрГУ, 2002. – 248 с.
В настоящее время теория вероятностей завоевала очень серьезное место в науке и прикладной деятельности. Её идеи, методы и результаты не только используются, но и буквально пронизывают все естественные и технические науки.
В нашу жизнь вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов. Общество все глубже начинает изучать себя и стремиться сделать прогнозы о себе самом и о явлениях природы, которые требуют представлений о вероятности. Теория вероятностей не обошла и учебные заведения.
В соответствии с федеральным компонентом Государственного стандарта образования и программу по математике за курс основной (средней) школы включены элементы комбинаторики, статистики и теории вероятностей. В последние годы в заданиях государственной итоговой аттестации (с настоящего года – обязательный государственный экзамен) и единого государственного экзамена по математике предлагаются задачи по теории вероятностей и комбинаторике. Поэтому при обучении математике необходима специальная подготовка по обучению учащихся решению таких задач.
В связи с чем цель нашего исследования: выделить основные методы и типы комбинаторных задач и подобрать комплекс таких задач.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой. Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать». Методы комбинаторики находят широкое применение в физике, химии, биологии, экономике, теории вероятностей и других областях науки.
В настоящее время практически во всех учебных пособиях по теории вероятностей выделяют следующие основные методы решения комбинаторных задач: перебор всех возможных вариантов (систематический перебор, перебор с ограничениями), полный граф, дерево вариантов (граф-дерево), таблица вариантов, правила произведения и суммы. Факториал. Перестановки. Размещения. Сочетания.
Формулы для подсчёта числа перестановок, размещений и сочетаний. Треугольник Паскаля. Бином Ньютона. Комбинированные задачи.
Проведенный анализ научно-методической литературы [1-5] позволил выделить следующие типы комбинаторных задач:
· задачи, в которых требуется перечислить все решения;
· задачи, состоящие в требовании выделить из всех возможных решений такое, которое удовлетворяет заданному дополнительному требованию;
· задачи, в которых требуется подсчитать число решений.
Процесс навыков подсчета комбинаторных объектов, по мнению Н.Ш. Кремера [4], можно расчленить на три этапа в зависимости от времени обучения и методов подсчета:
— подсчет методом непосредственного перебора;
— подсчет с использованием комбинаторных принципов;
— подсчет с использованием формул комбинаторики.
Для примера приведем несколько задач из составленного нами комплекса.
Операция перебора раскрывает идею комбинирования, служит основой для формирования комбинаторных понятий, поэтому на первом месте должна стоять задача по формированию навыков систематического перебора.
Пример 1. Из группы теннисистов, в которую входят четыре человека – Сидоров, Петров, Иванов и Шилов, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
Составим сначала все пары, в которые входит Сидоров (для краткости будем писать первые буквы фамилий). Получим три пары: СП, СИ, СШ.
Выпишем теперь пары, в которые входит Петров, но не входит Сидоров. Таких пар две: ПИ, ПШ.
Далее составим пары, в которые входит Иванов, но не входит Сидоров и Петров. Такая пара только одна: ИШ.
Других вариантов составления пар нет, так как все пары, в которые входит Шилов, уже составлены.
Итак, мы получили 6 пар: СП, СИ, СШ, ПИ, ПШ, ИШ. Значит, всего существует 6 вариантов выбора тренером пары теннисистов из данной группы.
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
Пример 2. Три подруги – Юля, Света и Катя – приобрели два билета на показ мод на 1-е и 2-е места первого ряда. Сколько у подруг есть вариантов занять эти два места в зале?
Если на показ мод пойдут Юля и Света, то они могут занять места двумя способами: 1-е место – Юля, 2-е – Света, или наоборот. Аналогично Юля и Катя, Света и Катя. Таким образом, мы получили 6 вариантов: ЮК, КЮ, ЮС, СЮ, КС, СЮ.
Пример 3. При встрече представителей большой восьмерки они обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Данную задачу возможно решить методом непосредственного перебора, и уже в самом начале заметим, что довольно сложно перебирать все возможные варианты и не запутаться, не говоря уже о записи решения этой задачи. Но, введя определенные обозначения — кодирование, решение будет очень легко представить.
Каждому представителю даем номер от 1 до 8, а рукопожатия закодируем следующим образом: например, число 24 означает что 2-ой представитель пожал руку 4-му. Причем число 35 и 53 означают одно и тоже рукопожатие, и брать будем меньшее из них. Коды рукопожатий мы можем оформить следующей таблицей:
12, 13, 14, 15, 16, 17, 18,
23, 24, 25, 26, 27, 28,
Таким образом, у нас получилось 1+2+3+4+5+6+7=28 рукопожатий.
Еще одним способом подсчета комбинаторных наборов является использование правила суммы.
Пример 4. Из класса нужно выделить одного дежурного, девочку или мальчика. Сколько существует способов для выбора дежурного, если в классе 20 мальчиков и 18 девочек?
Выбрать одного мальчика из 20 мы можем 20-ю способами, а одну девочку из 18 можно 18-тью способами. Тогда выбрать одного дежурного мальчика или девочку можно (18+20) способами.
Для подсчета вариантов мы использовали здесь правило суммы, которое можно сформулировать так: если два действия взаимно исключают друг друга, причем одно из них можно выполнить п способами, а другое – m способами, то какое-либо одно из них можно выполнить n+m способами. В нашем примере действия исключают друг друга, так как мы должны выбрать либо мальчика из одного множества, либо девочку из другого.
Пример 5. Преподаватель хочет назначить троих студентов для уборки аудитории. В группе двадцать семь студентов. Сколькими способами можно это сделать?
Решение. Так как порядок студентов не важен, используем формулу для числа сочетаний (выбор любых 3 элементов из 27):
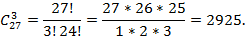
Пример 6. В классе из 25 учеников нужно выбрать четырех для научной конференции. Сколькими способами это можно сделать?
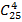
Решение. Так как порядок выбранных четырех учеников не имеет значения, то это можно сделать способами:
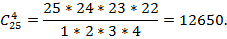
В рассмотренных примерах использовали формулу сочетания.
Пример 7. Имеются 3 путевки в санаторий. Сколько вариантов распределения можно составить для 5 претендентов?
Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.
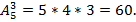
Пример 8. Расписание одного дня содержит 6 уроков. Определить количество таких расписаний при выборе из 12 дисциплин.
Решение. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.
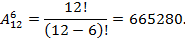
Примеры 7, 8 решались по формуле размещения.
Пример 9. Сколькими способами семь конфет разных марок можно расставить на прилавке в один ряд?
Решение: эта задача о числе перестановок семи разных конфет. По формуле получаем:
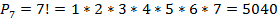
способов осуществить расстановку конфет.
Пример 10. На библиотечной полке стоят 10 книг, причем 8 — книги разных авторов и еще 2 книги автора. Сколькими способами можно расставить эти книги так, чтобы книги одного автора стояли рядом друг с другом?
Временно объединим три книги одного автора в один объект, всего получим 9 объектов — 8 книг и 1 объект из двух книг. Для них число перестановок будет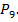 
Теперь три книги переставим между собой 
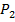способами. По правилу произведения получаем что число способов расставить книги нужным образом равно:
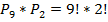
При подсчете конечного результата была использована формула перестановки.
Разработанный нами комплекс задач будет полезен, как учителям математики, так и студентам во время прохождения педагогической практики.
Источник: eduherald.ru
Комбинаторные задачи теории информации
В эту категорию попали задачи, имеющие отношение к теории информации, которые можно решить, в основном с применением формул комбинаторики для определения числа сочетаний, перестановок и т.д. Программная часть решения достаточно тривиальна, за исключением необходимости применять длинную арифметику.
Задача №292. Флаги на мачтах
Имеются n различных сигнальных флагов и k мачт, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке развешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми.
Решение
Каждый способ развешивания флагов можно осуществить в два этапа. На первом этапе мы переставляем всеми возможными способами данные n флагов. Это можно сделать n! способами. После этого берем один из способов распределения n одинаковых флагов по k мачтам. Число таких способов равно .
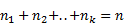
Пусть этот способ заключается в том, что на первую мачту надо повесить n1 флагов, на вторую n2 флагов, …, на k-ю nk флагов, где . Тогда берем первые n1 флагов данной перестановки, следующие n2 развешиваем на второй мачте и т.д. Ясно, что используя все перестановки n флагов и все способы распределения n одинаковых флагов по k мачтам, мы получим все способы решения поставленной задачи.
Задача №293. Полное число сигналов
Найдем полное число сигналов, которые можно передать с помощью n сигнальных флагов, вывешиваемых на k мачтах.
Решение
С помощью заданных s флагов можно передать 
сигналов. Но s флагов из n можно выбрать 
способами. Значит, полное число сигналов задается формулой:
Задача №294. Передача сигналов по времени
Сообщение передается с помощью сигналов нескольких типов. Длительность передачи сигнала первого типа равна t1, второго типа t2, …, k-го типа tk единиц времени. Сколько различных сообщений можно передать с помощью этих сигналов за T единиц времени?
При этом учитываются лишь «максимальные» сообщения, то есть сообщения, к которым нельзя присоединить ни одного сигнала, не выйдя за рамки отведенного для передачи времени.
Входные данные
В первой строке два числа T и k,не превышающие 10 5
Во второй строкеkцелых чисел через пробел t1t2 … tk–длительность передачи каждого сигнала.
Решение
Обозначим число сообщений, которые можно передать за время T через f(T).
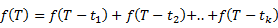
При этом f(T)=0, если T
Задача №295. Порождение комбинаторных объектов
Написать программу, которая печатает по одному разу все последовательности длины n, составленные из чисел 1..k (их количество равно k в степени n).
Рекурсивный перебор
Задача №296. Две кучки камней (acmp.ru)
У Вас есть N камней с массами W1, W2 , … WN. Требуется разложить камни на 2 кучки так, чтобы разница масс этих кучек была минимальной.
Входные данные
В первой строке входного файла INPUT.TXT записано число N – количество камней (1 ≤ N ≤ 18). Во второй строке через пробел перечислены массы камней W1, W2 , … WN (1 ≤ Wi ≤ 105).
Выходные данные
В единственную строку выходного файла OUTPUT.TXT нужно вывести одно неотрицательное целое число – минимально возможную разницу между массами двух кучек.
Пример
| input.txt | output.txt |
| 5 5 8 13 27 14 | 3 |
Решение
using namespace std;
int ar[20], n, mi = 987654321, sum = 0;
void p(int pos, int curSum)
mi = min(mi, abs(sum — 2*curSum));
Перебор без рекурсии
Алгоритм получения следующей перестановки в лексикографическом (алфавитном) порядке набора элементов An:
1. Просматриваем A1, . An с конца до тех пор, пока не попадется Aii+1. Если таковых нет, то генерация закончена.
2. Рассматриваем Ai+1, Ai+2, . An. Найдем первый с конца Am больший Ai и поменяем их местами.
3. Ai+1, Ai+2, . An переставим в порядке возрастания (для этого достаточно переписать с конца).
4. Печатаем найденную перестановку.
5. Возвращаемся к пункту 1.
Данный алгоритм уже реализован в C++. Воспользуемся функцией next_permutation(), описанной в библиотеке algorithm.
Алгоритм next_permutation() создает следующую перестановку заданной последовательности. Перестановка генерируется в предположении, что последовательность, отсортированная от меньшего к большему, представляет собой первую перестановку. Если следующей перестановки не существует, алгоритм next_permutation() сортирует последовательность в виде ее первой перестановки и возвращает значение false. В противном случае возвращается значение true.
Задача №297. Анаграмма (acmp.ru)
(Время: 1 сек. Память: 16 Мб)
Пусть задано некоторое слово, состоящее из букв английского алфавита длинной не более 80 символов (например, “WORD”). Рассмотрим набор возможных перестановок, состоящих из букв данного слова (например, “RDOW”, “WODR” и т.д.). Требуется выбрать из этого множества слово, следующее по алфавиту за исходным.
Входные данные
В единственной строке входного записано слово, не последнее по алфавиту среди возможных его перестановок.
Выходные данные
В единственную строку нужно вывести следующее слово по алфавиту.
Примеры
| № | INPUT.TXT | OUTPUT.TXT |
| 1 | abdc | acbd |
| 2 | word | wrdo |
Решение
Если пользоваться алгоритмом, описанным выше, то программа, реализующая получение следующей в лексикографическом порядке перестановки строки, выглядит так:
using namespace std;
int n=s.length()-1, i=n-1, m=n;
Источник: megaobuchalka.ru