Количество элементарных операций которые выполняет программа это

Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.

Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.

Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.

Виноват ли ЕГЭ в развале системы образования? И что делать?

Определения

Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.

Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.

Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.

Порядок роста сложности алгоритмов

Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.

Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.

Виды асимптотических оценок

O – оценка для худшего случая

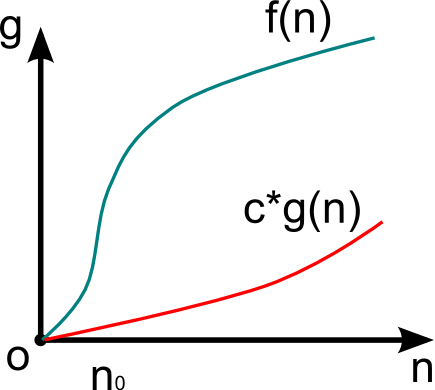
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n0 > 0, то
0 < f(n) < c*g(n),
для n > n0.

КВАНТОВЫЙ КОМПЬЮТЕР: ТОЛЬКО 3% ЛЮДЕЙ ЭТО ПОНИМАЮТ | ФОРМАТ

Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).

Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.

Примеры асимптотических функций

f(n) g(n)

2n 2 + 7n — 3	n 2
98n*ln(n)	n*ln(n)
5n + 2	n
8	1

Ω – оценка для лучшего случая

Определение схоже с определением оценки для худшего случая, однако
f(n) = Ω(g(n)), если
0 < c*g(n) < f(n)

Ω(g(n)) определяет класс функций, которые растут не медленнее, чем функция g(n) с точностью до константного множителя.

Θ – оценка для среднего случая

Стоит лишь упомянуть, что в данном случае функция f(n) при n > n0 всюду находится между c1*g(n) и c2*g(n), где c – константный множитель.
Например, при f(n) = n 2 + n; g(n) = n 2 .

Критерии оценки сложности алгоритмов

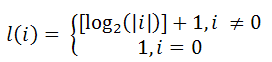
Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.

Временная сложность при ЛВК определяется значением l(Op), где Op – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.

Пример оценки сложности при вычислении факториала

Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:

void main()

Временная сложность при равномерном весовом критерии

Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).

Таким образом, временная сложность при РВК равна O(n).

Временная сложность при логарифмическом весовом критерии

В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.

Итак, в данной задаче выделяется три операции:

1) i

На i-м шаге получится log(n).
Так как шагов (n-1), сложность данной операции составит (n-1)*log(n).

2) i = i + 1

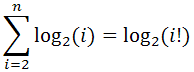
На i-м шаге получится log(i).
Таким образом, получается сумма .

3) result = result * i

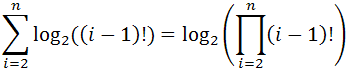
На i-м шаге получится log((i-1)!).
Таким образом, получается сумма .

Если сложить все получившиеся значения и отбросить слагаемые, которые заведомо растут медленнее с увеличением n, получим конечное выражение .

Ёмкостная сложность при равномерном весовом критерии

Здесь всё просто. Необходимо подсчитать количество переменных. Если в задаче используются массивы, за переменную считается каждая ячейка массива.
Так как количество переменных не зависит от размера входа, сложность будет равна O(1).

Ёмкостная сложность при логарифмическом весовом критерии

В данном случае следует учитывать максимальное значение, которое может находиться в ячейке памяти. Если значение не определено (например, при операнде i > 10), то считается, что существует какое-то предельное значение Vmax.
В данной задаче существует переменная, значение которой не превосходит n (i), и переменная, значение которой не превышает n! (result). Таким образом, оценка равна O(log(n!)).

Выводы

Изучение сложности алгоритмов довольно увлекательная задача. На данный момент анализ простейших алгоритмов входит в учебные планы технических специальностей (если быть точным, обобщённого направления «Информатика и вычислительная техника»), занимающихся информатикой и прикладной математикой в сфере IT.
На основе сложности выделяются разные классы задач: P, NP, NPC. Но это уже не проблема теории асимптотического анализа алгоритмов.

• теория алгоритмов
• оценка алгоритмов
• алгоритмы
• асимптотический анализ алгоритмов

Источник: habr.com

Сложность алгоритмов.

Большинство задач могут быть решены по-разному, с помощью разных алгоритмов. Поэтому возникает вопрос: как выбрать лучший? И ещё один важный вопрос — способен ли современный компьютер за приемлемое время найти решение задачи? Например, в игре в шахматы возможно лишь конечное количество позиций и, следовательно, только конечное количество различных партий.

Значит, теоретически можно перебрать все возможные партии и выяснить, кто побеждает при правильной игре — белые или чёрные. Однако количество вариантов настолько велико, что современные компьютеры не могут выполнить такой перебор за приемлемое время.

Что мы хотим от алгоритма? Во-первых, чтобы он работал как можно быстрее. Во-вторых, чтобы объём необходимой памяти был как можно меньше. В-третьих, чтобы он был как можно более прост и понятен, что позволяет легче отлаживать программу. К сожалению, эти требования противоречивы, и в серьёзных задачах редко удаётся найти алгоритм, который был бы лучше остальных по всем показателям.

Часто говорят о временной сложности алгоритма (быстродействии) и пространственной сложности, которая определяется объёмом необходимой памяти.

Временем работы алгоритма называется количество элементарных операций T, выполненных исполнителем.

Такой подход позволяет оценивать именно качество алгоритма, а не свойства исполнителя (например, быстродействие компьютера, на котором выполняется алгоритм). При этом мы считаем, что время выполнения всех элементарных операций одинаково.

Как правило, величина Т будет существенно зависеть от объёма исходных данных: поиск в списке из 10 элементов завершится гораздо быстрее, чем в списке из 10000 элементов. Поэтому сложность алгоритма обычно связывают с размером входных данных N и определяют как функцию T(N). Например, для алгоритмов обработки массивов в качестве размера N используют длину массива. Функция T(N) называется временной сложностью алгоритма.

Временная сложность агоритма определяется функцией T(N) = 2N 3 . Во сколько раз увеличится время работы алгоритма, если размер данных N увеличится в 10 раз?

Пространственная сложность — это зависимость объёма занимаемой памяти от размера данных N. Для ускорения работы некоторых алгоритмов нужно использовать дополнительную память, которая может быть намного больше, чем память для хранения исходных данных.

Для быстрой сортировки массива из N элементов с помощью алгоритма Семёна требуется N вспомогательных массивов, каждый из которых содержит N элементов. Как изменится объём нужной дополнительной памяти, если N увеличится в 10 раз?

Поскольку память постоянно дешевеет, а быстродействие компьютеров растёт медленно, более важна временная сложность алгоритмов. Пространственную сложность мы дальше рассматривать не будем.

Примеры вычисления сложности

Рассмотрим алгоритмы выполнения различных операций с массивом А длины N, который может быть объявлен в программе так:

целтаб А[1:N] var A: array[1..N] of integer;

Пример 1. Вычислить сумму значений первых трёх элементов массива (при N ? 3).

Решение этой задачи содержит всего один оператор:

Этот алгоритм включает две операции сложения и одну операцию записи значения в память, поэтому его сложность T(N) = 3 не зависит от размера массива вообще.

Вычислите количество операций (считая сравнения и присваивание значений переменным) при выполнении фрагмента программы:

Пример 2. Вычислить сумму значений всех элементов массива.

В этой задаче уже не обойтись без цикла:

Здесь выполняется N операций сложения и N + 1 операция записи в память, поэтому его сложность T(N) = 2N + 1 возрастает линейно с увеличением длины массива.

Вычислите количество операций при выполнении фрагмента программы:

Пример 3. Отсортировать все элементы массива по возрастанию методом выбора. Напомним, что метод выбора предполагает поиск на каждом шаге минимального из оставшихся неупорядоченных значений (здесь i, j, nMin и с — целочисленные переменные):

Подсчитаем отдельно количество сравнений и количество перестановок. Количество сравнений элементов массива не зависит от данных и определяется числом шагов внутреннего цикла:

Здесь использована формула для суммы первых N — 1 членов арифметической прогрессии.

На каждом шаге внешнего цикла происходит перестановка двух элементов, общее количество перестановок равно Тn( N) = N -1, т. е. сложность по перестановкам — линейная.

Определите количество операций при вычислении суммы значений элементов квадратной матрицы А размером N х N (здесь i, j и Sum — целочисленные переменные):

По результатам этих примеров можно сделать выводы:

• простой цикл, в котором количество шагов пропорционально N, — это алгоритм линейной сложности;
• вложенный цикл, в котором количество шагов внешнего и внутреннего цикла пропорционально N, — это алгоритм квадратичной сложности.

Что такое асимптотическая сложность?

Допустим, что нужно сделать выбор между несколькими алгоритмами, которые имеют разную сложность. Какой из них лучше (работает быстрее)? Оказывается, для этого необходимо знать размер массива данных, которые нужно обрабатывать. Сравним, например, три алгоритма, сложность которых

T1(N) = 10000 • N, T2(N) = 100 • N 2 и T3(N) = N 3 .

Построим эти зависимости на графике (рис. 4.5). При N ? 100 получаем Т3(N) < T2(N) < T1N), при N = 100 количество операций для всех трёх алгоритмов совпадёт, а при больших N имеем Т3(N) > T2(N) > T1N).

Рис. 4.5

Обычно в теоретической информатике при сравнении алгоритмов используется их асимптотическая сложность, т. е. скорость роста количества операций при больших значениях N.

Запись 0(N) (читается «О большое от N») обозначает линейную сложность алгоритма. Это значит, что, начиная с некоторого значения N = N0, количество операций будет меньше, чем с•N, где с — некоторая постоянная:

При увеличении размера данных в 10 раз объём вычислений алгоритма с линейной сложностью увеличивается тоже примерно в 10 раз.

Пусть, например, T(N) = 2N — 1, как в алгоритме поиска суммы значений элементов массива. Очевидно, что при этом T(N) ? 2N для всех N ? 1, поэтому алгоритм имеет линейную сложность.

Определите любые подходящие значения с и N0, такие что T(N) ? с•N для N ? N0, для алгоритмов с линейной асимптотической сложностью:

Многие известные алгоритм имеют квадратичную сложность 0(N 2 ). Это значит, что сложность алгоритма при больших N меньше, чем с•N 2 :

Если размер данных увеличивается в 10 раз, то количество операций (и время выполнения такого алгоритма) увеличивается примерно в 100 раз. Пример алгоритма с квадратичной сложностью — сортировка методом выбора, для которой число сравнений

Определите любые подходящие значения с и N0, такие что T(N) ? с•N 2 для N ? N0, для алгоритмов с квадратичной асимптотической сложностью:

a) T(N) = 5N 2 — 3N — 2;

б) T(N) = 7N 2 — 3N — 5.

Алгоритм имеет асимптотическую сложность 0(f(N)), если найдется такая постоянная с, что, начиная с некоторого N = N0, выполняется условие T(N)?c•f(N).

Это значит, что график функции с•f(N) проходит выше, чем график функции T(N), по крайней мере, при N?N0 (рис. 4.6).

Рис. 4.6

Если количество операций не зависит от размера данных, то говорят, что асимптотическая сложность алгоритма 0(1), т. е. количество операций меньше некоторой постоянной при любых N.

Существует также немало алгоритмов с кубической сложностью 0(N 3 ). При больших значениях N алгоритм с кубической сложностью требует большего количества вычислений, чем алгоритм со сложностью 0(N 2 ), а тот, в свою очередь, работает дольше, чем алгоритм с линейной сложностью. Однако при небольших значениях N всё может быть наоборот, это зависит от постоянной с для каждого из алгоритмов.

Известны и алгоритмы, для которых количество операций растёт быстрее, чем любой многочлен, например как 0(2 N ) или 0(N!), где N! обозначает факториал числа N — произведение всех натуральных чисел от 1 до N : N! = 1 • 2 • 3 •… • N. Такие алгоритмы встречаются чаще всего в задачах поиска оптимального (наилучшего) варианта, которые решаются только методом полного перебора. Самая известная задача такого типа — это задача коммивояжёра (бродячего торговца), который должен посетить по одному разу каждый из указанных городов и вернуться в начальную точку. Для него нужно выбрать маршрут, при котором стоимость поездки (или общая длина пути) будет минимальной.

В таблице 4.1 показано примерное время работы алгоритмов, имеющих разную временную сложность, при N = 100 на компьютере с быстродействием 1 миллиард операций в секунду.

Таблица 4.1

T(N)	Время выполнения
N	100 нc
N 2	10 мс
N 3	0,001 с
2 N	10 13 лет

Юный программист Григорий поспорил с учителем, что сможет к завтрашнему уроку с помощью компьютера решить сложную задачу перебора вариантов. Дома он определил временную сложность алгоритма: T(N) = 2 N . Для какого наибольшего значения N сможет Григорий решить задачу за сутки, если его компьютер выполняет 1 миллиард операций в секунду?

Выводы

• Временем работы алгоритма называется количество элементарных операций Т, выполненных исполнителем.
• Временная сложность алгоритма обычно зависит от объёма исходных данных N, например от размера массива.
• Пространственная сложность — это объём памяти, необходимой для работы алгоритма.
• Простой цикл, в котором количество шагов пропорционально N, — это алгоритм линейной сложности.
• Вложенный цикл, в котором количество шагов внешнего и внутреннего цикла пропорционально N, — это алгоритм квадратичной сложности.
• Алгоритм имеет асимптотическую сложность 0(f(N)), если найдётся такая постоянная с, что, начиная с некоторого N = N0, выполняется условие T(N) ? с • f(N).
• Линейная сложность означает, что при увеличении размера массива в К раз количество операций увеличивается примерно в К раз.
• Квадратичная сложность означает, что при увеличении размера массива в К раз количество операций увеличивается примерно в К 2 раз.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Какие критерии используются для оценки алгоритмов?
2. Почему скорость работы алгоритма оценивается не временем выполнения, а количеством элементарных операций?
3. Как учитывается размер данных при оценке быстродействия алгоритма?
4. В каких случаях алгоритм, имеющий асимптотическую сложность 0(N 2 ), может работать быстрее, чем алгоритм с асимптотической сложностью 0(N)?
5. Выполните по указанию учителя задания в рабочей тетради.

Подготовьте сообщение

§22. Сложность алгоритмов.

Источник: murnik.ru

Временная и пространственная сложности

Теория сложности вычислений возникла из потребности сравнивать быстродействие алгоритмов, чётко описывать их поведение (время исполнения и объём необходимой памяти) в зависимости от размера входа и выхода.

Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.

Временная сложность алгоритма (в худшем случае) — это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. В задачах, где размер выхода не превосходит или пропорционален размеру входа, можно рассматривать временную сложность как функцию размера только входных данных.

Аналогично понятию временной сложности в худшем случае определяется понятие временная сложность алгоритма в наилучшем случае. Также рассматривают понятие среднее время работы алгоритма, то есть математическое ожидание времени работы алгоритма. Иногда говорят просто: «Временная сложность алгоритма» или «Время работы алгоритма», имея в виду временную сложность алгоритма в худшем, наилучшем или среднем случае (в зависимости от контекста).

По аналогии с временной сложностью, определяют пространственную сложность алгоритма, только здесь говорят не о количестве элементарных операций, а об объёме используемой памяти.

Основы оценок сложности алгоритмов

Нам уже известно, что правильность — далеко не единственное качество, которым должна обладать хорошая программа. Одним из важнейших является эффективность, характеризующая прежде всего время выполнения программы для различных входных данных (параметра ).

Нахождение точной зависимости для конкретной программы — задача достаточно сложная. По этой причине обычно ограничиваются асимптотическими оценками этой функции, то есть описанием ее примерного поведения при больших значениях параметра . Иногда для асимптотических оценок используют традиционное отношение (читается >) между двумя функциями , определение которого можно найти в любом учебнике по математическому анализу, хотя чаще применяют отношение эквивалентности (читается >).

Легко видеть, что количество операций, которые должны быть выполнены для нахождения факториала числа в первом приближении прямо пропорционально этому числу, ибо количество повторений цикла (итераций) в данной программе равно . В подобной ситуации принято говорить, что программа (или алгоритм) имеет линейную сложность.

Можно ли вычислить факториал быстрее? Оказывается, да. Можно написать такую программу, которая будет давать правильный результат для тех же значений , для которых это делают все приведенные выше программы, не используя при этом ни итерации, ни рекурсии. Ее сложность будет , что фактически означает организацию вычислений по некоторой формуле без применения циклов и рекурсивных вызовов!

Не менее интересен и пример вычисления -го числа Фибоначчи. В процессе ее исследования фактически уже было выяснено, что ее сложность является экспоненциальной и равна . Подобные программы практически не применимы на практике. В этом очень легко убедиться, попробовав вычислить с ее помощью 40-е число Фибоначчи. По этой причине вполне актуальна следующая задача.

Вот решение этой задачи, в котором переменные j и k содержат значения двух последовательных чисел Фибоначчи.

Текст программы.

public class FibIv1

public static void main(String[] args) throws Exception

int n = Xterm.inputInt(«Введите n -> «);

Xterm.print(» не определеноn»);

Xterm.println(» /html/1546/187/html_bmpS6vBQIR.FGYa/img-ZSuLDB.png» name=»Рисунок 28″ align=»bottom» width=»16″ height=»17″ border=»0″>-ого числа Фибоначчи , которую легко проверить для небольших значений:

Может показаться, что основываясь на ней, легко написать программу со сложностью , не использующую итерации или рекурсии.

Текст программы.

public class FibIv2

public static void main(String[] args) throws Exception

int n = Xterm.inputInt(«Введите n -> «);

double f = ( 1.0 + Math.sqrt(5.) ) / 2.0;

int j = (int)( Math.pow(f,n) / Math.sqrt(5.) + 0.5 );

Xterm.println(«f(» + n + «) /html/1546/187/html_bmpS6vBQIR.FGYa/img-6PDjlW.png» name=»Рисунок 40″ align=»bottom» width=»51″ height=»34″ border=»0″>). Про алгоритмы, в которых количество операций примерно пропорционально (в информатике принято не указывать основание двоичного логарифма) говорят, что они имеет логарифмическую сложность ( ).

Для вычисления n-го числа Фибоначчи существует такой алгоритм, программную реализацию которого мы приведем без дополнительных комментариев, — иначе нужно объяснять слишком много (связь чисел Фибоначчи со степенями матрицы порядка два, использование классов для работы с матрицами, алгоритм быстрого возведения матрицы в степень).

Текст программы.

public class FibIv3

public static void main(String[] args) throws Exception

int n = Xterm.inputInt(«Введите n -> «);

Xterm.println(» не определено»);

Xterm.println(» /html/1546/187/html_bmpS6vBQIR.FGYa/img-O9Jjqm.png» name=»Рисунок 55″ align=»bottom» width=»43″ height=»34″ border=»0″> , , 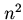и соответственно. Предположим, что второй из этих алгоритмов требует для своего выполнения на некотором компьютере при значении параметра ровно одну минуту времени. Тогда времена выполнения всех этих четырех алгоритмов на том же компьютере при различных значениях параметра будут примерно такими, как в таблице.

Источник: studfile.net