Код программы в матлабе

После лабораторных работ (Решение систем линейных алгебраических уравнений, Методы численного интегрирования, Численное дифференцирование функций, Приближенные методы решения обыкновенных дифференциальных уравнений, Аппроксимация функций) часто следует курсовая работа. В последнее время я ничего не публиковал из университетских работ. Но я не бездельничал — в курсовой работе много графиков, формул и таблиц…

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

Задачей данной курсовой работы является практическое применение методов вычислительной математики для расчёта электрической цепи.

Задание.

Рассчитать выбранную согласно варианту электрическую схему (см. «Варианты электрических цепей») тремя способами. Провести анализ полученных результатов.

Расчёт необходимо произвести следующими способами:

1. Вручную: расчёт осуществляется по приведенным формулам (см. «Теоретические сведения») выбранной методики расчёта (см. «Методы расчёта»).
2. Программно: расчёт цепи осуществляет программа, в которой реализованы необходимые методы вычислительной математики (см. «Вспомогательные методы»).
3. С помощью схемного эмулятора Electronics Workbench12: выбранная схема «собирается» в Electronics Workbench 5.12 и расчёт осуществляется с его помощью.

Выбор методики расчёта:

Beyond the Code: Showcasing Your MATLAB Results Like a Pro

Формулы для вычисления индивидуального задания:

№ электрической схемы=(№ студента по списку + 2*(№ группы-40)) mod 16+1

№ метода решения системы уравнений =№ студента по списку mod 5+1

№ метода вычисления определителя =№ студента по списку mod 2+1

№ метода вычисления обратной матрицы=№ студента по списку mod 2+1

Согласно этим формулам:

№ электрической схемы=(13 + 2*(42-40)) mod 16+1=(13+2*2) mod 16+1=17 mod 16 +1=1+1=2.

№ метода решения системы уравнений = 13 mod 5+1=3+1=4

№ метода вычисления определителя =13 mod 2+1=1+1=2

№ метода вычисления обратной матрицы=13 mod 2+1=1+1=2

Метод решения системы уравнений:

Метод вычисления определителей:

По определению: с использованием алгебраических дополнений

Метод вычисления обратной матрицы:

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ВЫБРАННОМУ МЕТОДУ РАСЧЁТА ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

При расчёте электрических цепей используются два закона Кирхгофа.

Первый закон Кирхгофа, или закон Кирхгофа для узлов:

Сумма токов, расходящихся от узла электрической цепи, равна нулю.

При составлении уравнений согласно первому закону Кирхгофа необходимо задаться условно-положительными направлениями токов во всех ветвях, обозначив их на схеме стрелками. В левой части уравнения следует ставить знак «плюс» перед буквенными обозначениями токов, положительное направление которых принято от узла, и знак «минус» перед буквенными обозначениями токов, положительное направление которых принято к узлу. Для случая, представленного на рисунке следует написать:

Использование унаследованного кода в MATLAB: Интеграция С/С++

Если в результате расчёта будет получено для некоторого тока в некоторый момент времени положительное число, то это значит, что ток имеет в данный момент времени действительное направление согласно стрелке. Если же будет получено отрицательное значение, то этот тот в действительности направлен против стрелки.

Второй закон Кирхгофа, или закон Кирхгофа для контуров.

Сумма падений напряжения во всех ветвях любого замкнутого контура электрической цепи равна сумме ЭДС источников энергии, действующих в этом контуре.

Для составления уравнений согласно второму закону Кирхгофа должны быть заданы положительные направления токов ik и ЭДС ek источников энергии во всех ветвях.

Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.
Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На рисунке в качестве примера изображена двухконтурная схема, в которой I11 и I22 — контурные токи.

Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно.

Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

Перегруппируем слагаемые в уравнениях

Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы

Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.

где R12 — общее сопротивление между первым и вторым контурами;
R21 — общее сопротивление между вторым и первым контурами.
E11 = E1 и E22 = E2 — контурные ЭДС.
В общем виде уравнения (4.4) и (4.5) записываются следующим образом:

Собственные сопротивления всегда имеют знак «плюс».
Общее сопротивление имеет знак «минус», если в данном сопротивлении контурные токи направлены встречно друг другу, и знак «плюс», если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (1) и (2) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.

УТОЧНЕНИЕ ЗАДАНИЯ:

В силу специфики итерационного метода Гаусса-Зейделя система составленная система уравнений может не сойтись. Скорее всего система уравнений, составленная просто применением законов Кирхгофа не сойдётся, так как в уравнениях, составленных для узлов системы модули диагональных коэффициентов будут либо равны нулю, либо единице. Но и в том и в другом случае они будут меньше сумм модулей всех остальных коэффициентов. Следовательно, метод Гаусса-Зейделя скорее всего не сойдётся на системе уравнений, составленной прямым применением законов Кирхгофа.

В связи с описанной выше проблемой система уравнений будет составляться методом контурных токов (хотя в определённых условиях метод Гаусса-Зейделя может не сойтись и для этой системы). Но прямое применение законов Кирхгофа всё равно необходимо, так как после применения метода контурных токов будут получены только контурные токи, но не сами токи схемы. По уравнениям, составленным по законам Кирхгофа, предполагается вычислять истинные значения токов схемы.

РУЧНОЙ МЕТОД РАСЧЁТА

Для расчёта обозначим на схеме элементы:

Приведённую выше схему можно упростить.

Резисторы R4 и R5 соединены последовательно, следовательно, их можно объединить в один. Объединённый резистор назовём R45. Его сопротивление будет равно R45=R4+R5.

Резисторы R7 и R10 соединены последовательно, следовательно, их можно объединить в один. Назовём его R710. Его сопротивление будет равно R710=R7+R10.

В результате преобразований получим следующую схему:

В схеме только резисторы и источники тока и напряжения. Решим схему методом контурных токов. Расставим направления токов, обозначим и обозначим направления контурных токов:

Непосредственно применим правила Кирхгофа. Это пригодится в дальнейшем для вычисления токов из контурных токов:

На рисунке изображено 6 узлов, но важны только 5. Шестой узел не даёт новой информации. Запишем уравнения по первому закону Кирхгофа для пяти узлов:

1. i1+i4-i5=0
2. –i1+i3+i2+I1=0
3. –I1+i6-i7+i8=0
4. –i8-i2+i9=0
5. –i9+i7+i10+i5=0

Теперь запишем уравнения по второму закону Кирхгофа. Чтобы не загромождать рисунок на нём не были обозначены направления напряжений. Направления напряжения будем считать совпадающим с направлением токов. Например, uR1 имеет направление от узла 1 к узлу 2, uR2 имеет направление от узла 2 к узлу 4.

Уравнения, записанные по второму закону Кирхгофа:

Заменим напряжения через токи по формуле u=i*R:

Следовательно, исходное задание сводится к решению системы уравнений:

Теперь заменим источник тока I1 на эквивалентный источник ЭДС E5. E5=(R2+R6*R9/(R6+R9))I1. Тогда получится следующая схема:

Составим уравнения для полученных контуров:

Теперь выразим токи через контурные токи.

Для ручного метода расчёта уравнения были записаны в матричной форме.

Источник: urvanov.ru

Документирование функций Matlab

Документирование функций Matlab — способ передачи кода программ, написанных на языке Matlab коллегам или в общественное пользование. Система Matlab имеет ряд инструментов для работы с документированными функциями. В частности:

1. заголовок функции показывается в поле «Description» окна «Current Directory»;
2. заголовок функции и ссылка на файл, содержащий функцию показываются при генерации содержания «View->Directory Reports->Contents Report»;
3. документация функции «help myfunc» показывается в окне «Command Window»;
4. документация функции «doc myfunc» показывается в окне «Help»;
5. список незавершенных работ и работ, требующих пересмотра показывается при генерации отчета «View->Directory Reports->TODO/FIXME Report».

М-файл содержит необязательное ключевое слово function начала тела функции

function [argOut1 {, argOut}] = myfunc(argIn {, arginN})
% NLINFIT Nonlinear least-squares regression function [beta,r,J,Sigma,mse] = nlinfit(X,y,model,beta,options)

или второй строкой:

function [beta,r,J,Sigma,mse] = nlinfit(X,y,model,beta,options) % NLINFIT Nonlinear least-squares regression

Описание функции

Описание содержит следующие необязательные секции: Description, Syntax, Arguments, Examples, See also. Например:

function hist = histmake(x, n, w) % make histogram using data sample, number of segments or their width % % hist = histmake(x, n, w) % % Arguments % x [N, 1] the input sample % n [int] optional number of segments to divide (xmin xmax) uniformly % w [scalar] optional width of a segment to divide (xmin xmax) uniformly % w [W,1] the edges of the histogram, assigned directly % if w is given, n will be ignored % if neither n nor w are given, the optimal value of n will be chosen % % hist [structure] to use in the toolbox with the following fields % .dom = [min(x), max(x)] the input domain % .edges = edges (start points) of the segments % .p = probabilities, non-cumulative % .N = length(x) % % Example % hist = histmake(randn(100,1), 5) % h = histplot(hist); % % See also % histnorm histprob histplot histc % % Revisions % Author: Paul Fleury, Date: 12/03/2005 % Supervisor: Vadim Strijov, Date: 24/03/2005 % Author: (Next revision author), Date: (Next revision date) %

1. желательно указывать размерность векторов и матриц, особенно, если используются несколько матриц связанной размерности;
2. желательно для каждой функции подготовить примеры использования, чтобы иметь возможность проиллюстрировать или протестировать ее работу;
3. если функция является частью системы, указать, какие функции могут использоваться совместно с данной.

Язык документирования

Можно документировать как по-русски, так и по-английски. При этом нужно помнить, что Matlab не поддерживает русский язык полностью. В ранних версиях при отображении русских комментариев в окне редактора могут появляться вопросы. В поздних версиях при создании отчета например, на языке TeX, русский язык может отображаться в некорректной кодировке.

Тело функции

Рекомендуется при создании черновых версий алгоритмов использовать ключевые слова

% TODO % FIXIT % NOTE

Эти слова могут быть использованы для планирования дальнейшей работы; см. генератор отчетов «View->Directory Reports->TODO/FIXME Report».

Соглашение об именах переменных

Рекомендуется давать переменным «говорящие» имена в формате Camel. Например:

• LogicRule — логическое правило (без префикса),
• strPatientName — имя пациента (строка),
• idxFeature — номер признака (целочисленный индекс),
• tsElConsumption — временной ряд потребления электроэнергии (структура типа ts — time series).

Так как типов в Матлабе в строгом смысле этого слова нет, то эти необязательные префиксы несут смысловую нагрузку. Часто используемые обозначения:

• idx — индекс элемента вектора,
• fea — признак,
• obj — объект,
• cls — класс,
• str — строка,
• vec — вектор,
• mat — матрица.

Имена функций обычно даются без префикса, за исключением

• demoAlgorithmName — демонстрационный файл или отчет о вычислительном эксперименте,
• loadDataName — файл порождения модельных данных или загрузки реальных данных.

Имена файлов специального назначение, которые будут работать в составе некоторой системы, даются в формате Camel. Файлы общего назначения получают краткое название с маленькой буквы.

Создание отчетов о вычислительных экспериментах

M-файлы, не использующие ключевое слово function, называются скриптами. Matlab предлагает язык разметки скриптов, удобный для автоматической генерации отчета о вычислительном эксперименте.

Для генерации отчета нужно выполнить команду publish, например,

publish(‘report_example’,’html’)

или выбрать «File->Publish to HTML».

Источник: www.machinelearning.ru

Команды Matlab — Список базовых команд

Это сокращенно как язык на основе матрицы, был разработан для компьютерных ученых и инженеров. Matlab предлагает отличные решения в вычислительной математике.

Matlab можно использовать для —

1. Анализ данных
2. Разработка алгоритма
3. Создание моделей и приложений

Matlab находит отличный пример использования в машинном обучении и глубоком обучении, поскольку они имеют дело с n-мерным пространством, которое может быть представлено и проанализировано только в матричной форме. Помимо этого, другими технологиями, использующими это, являются проектирование системы управления, обработка изображений и вычислительные финансы.

Команды Matlab

Matlab предоставляет команды, которые используются, пока пользователь должен взаимодействовать с приложением, используя интерфейс командной строки. Здесь мы увидим, как использовать эти команды в Matlab с помощью примеров

Основные команды Matlab

1. Очистить — эта команда удаляет переменные из памяти

2. Exist — эта команда проверяет наличие переменной

3. Clc — эта команда Matlab очищает окно команд

4. Global — эта команда объявляет переменную как глобальную

5. Справка — если вам нужно найти какую-либо помощь, просто напишите ключевое слово в окне командной строки, и оно отобразит ваши доступные параметры

6. Кто — эта команда Matlab перечисляет текущую переменную

7. Тип — эта команда отображает содержимое файла.

8. Pwd — эта команда отображает текущий каталог.

9. Дата — эта команда отображает текущую дату

10. Что — эта команда выводит список всех файлов Matlab в текущем каталоге

Пример 1:

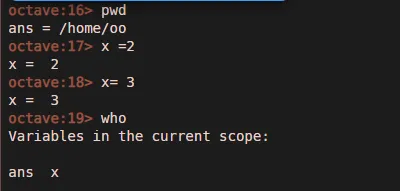
Пример 2:

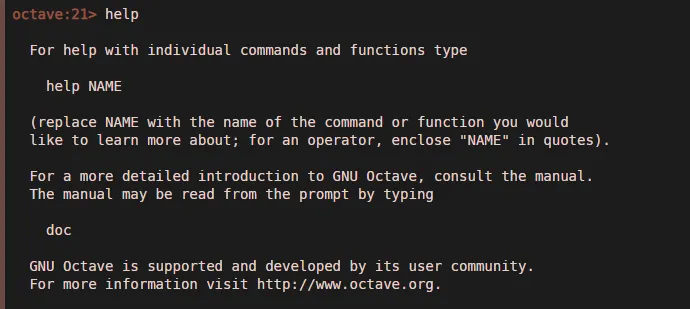
Пример 3:

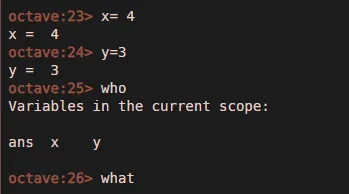
Пример 4:

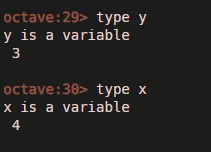
Пример 5:

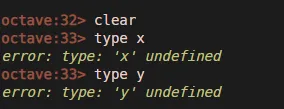
Таким образом, если вы четко соблюдаете пример 5, представленный выше, вы можете видеть, что операторы верны, и в последнем примере мы сначала вызвали команду clear, а затем мы искали тип x и y, который теперь оказался неопределенным, но не был так в примере 4.

Обратите внимание, что эти примеры были представлены с октавой, которая имеет открытый исходный код и эквивалентна платформе Matlab и использует тот же набор команд.

Промежуточные команды Matlab

Ниже приведены промежуточные команды Matlab:

1. Математические функции

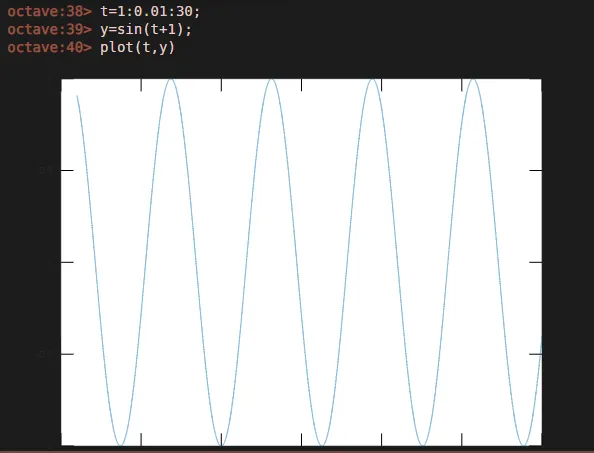
Здесь мы исследуем команду заговора, которая используется для построения кривой синусоидальной волны во времени, где время находится в диапазоне от 1 до 30 и увеличивается с интервалами 0, 01.

Аналогичным образом, мы можем сделать это для любой другой тригонометрической функции, которая составляет основную часть математики

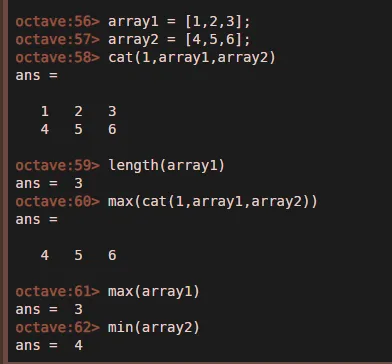
2. Команды, связанные с массивом

• Cat– используется для объединения двух массивов; первый аргумент, который он принимает, — это размер создаваемого массива, например, 1D, 2D или n-мерный массив, и после этого n-количество массивов передается в качестве аргументов, т.е. должны быть объединены, как показано на снимке
• Длина — вычисляет количество элементов в массиве
• Min, max — эти команды возвращают элементы max и min, присутствующие в массивах.

3. Матричные команды

• Eye — это создает матрицу идентичности
• Единицы — Это создает массив из них
• Нули — это создает массив нулей

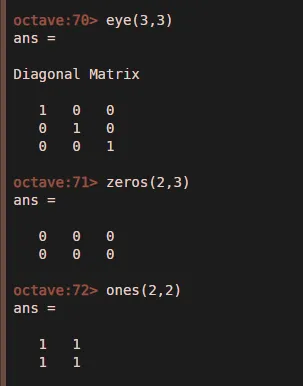
4. Матричная арифметическая команда

• Dot — эта команда Matlab генерирует скалярное произведение двух матриц, обратите внимание, что столбцы и строки матрицы определяют итоговое создание матрицы
• Cross — Синонимно это создает перекрестный продукт, полезный в векторных операциях, когда представлен в матричной форме

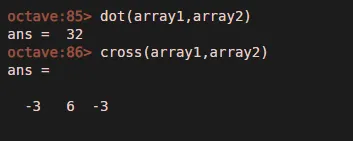
5. Матричные команды для операций, связанных с линейным уравнением

• Ранг — Эта команда предоставляет результат важному математическому параметру матриц, называемому рангом, который является количественным определением самого низкого порядка ненулевого определителя, несущего подматрицу в родительской матрице.
• Det — Определитель матрицы вычисляется с помощью этой команды.
• Inv — Выполнение этой команды предоставляет нам обратную матрицу.

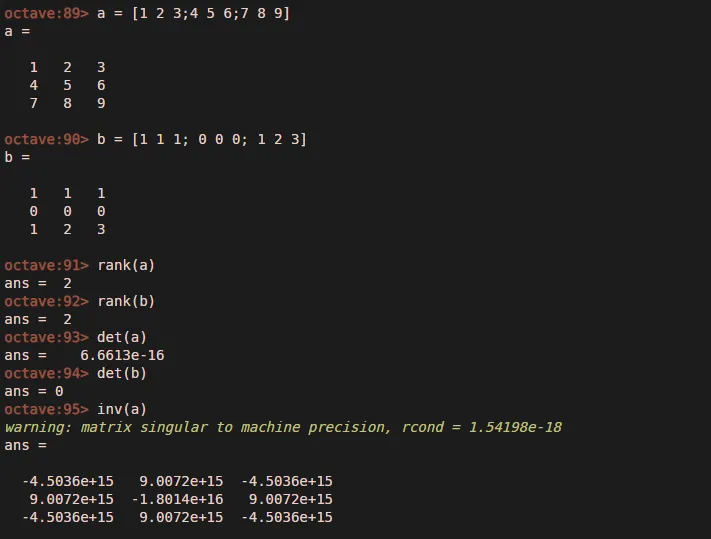
6. Сроки связанные команды

Cputime — вычисляет время процессора в секундах

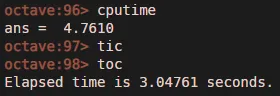
7. Строка Связанные команды

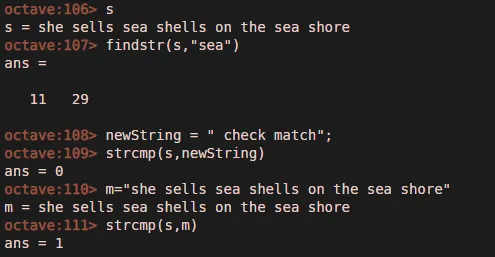
• Findstr — находит начальный индекс вхождений строки во фразе.
• Strcmp — эта команда используется для сравнения двух строк, возвращает 1, если совпадение правильное, иначе возвращает 0.

Расширенные команды Matlab

Давайте посмотрим на некоторые команды Advanced Matlab, которые приведены ниже:

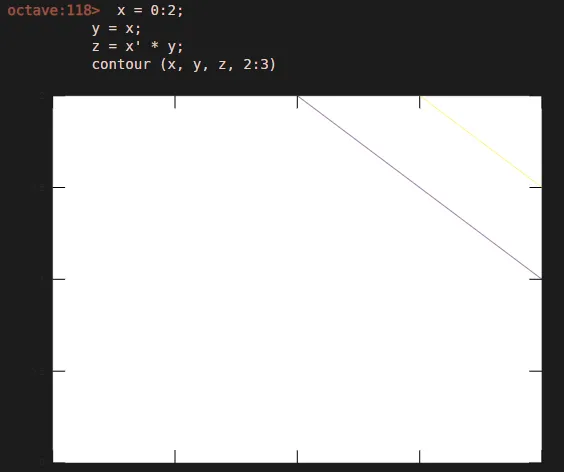
1. Контур

Всякий раз, когда вы занимаетесь проектированием систем управления в инженерном деле, контуры графиков Найквиста и т. Д. Дают вам знак стабильности в системе, мы можем настроить стиль графика в Matlab (например, цвет, тип линий и т. Д.).

2. Полиномиальные команды

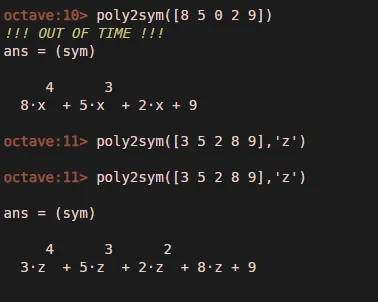
• Poly2sym (vector) — эта команда Matlab преобразует вектор коэффициентов в соответствующий символьный полином (от наивысшей к наименьшей степени).
• poly2sym (vector, ‘v’) — эта команда преобразует вектор коэффициентов в соответствующий символьный полином inv (от наивысшей до наименьшей степени).

3. Команды для решения уравнений

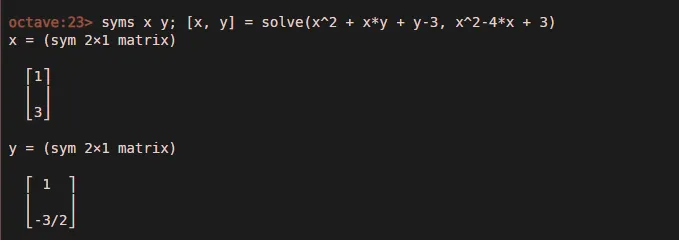
syms x1 x2… xn; решить (eq1, eq2, …, eqn, x1, x2, …, xn) — эта команда решает одновременно n чисел уравнений, и решения по ним присваиваются переменным в диапазоне от x1, x2 до xn.

Ниже прикрепленное изображение несет демонстрацию

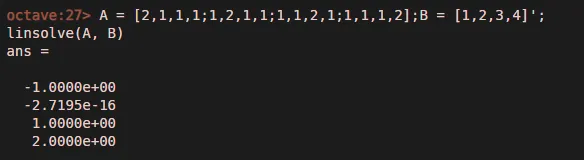
4. Команды для решения линейной системы уравнений

X = linsolve (A, B) — предположим, что нам нужно найти решение по данному уравнению

Это может быть решено в соответствии с приложенным изображением

Советы и рекомендации по использованию команд Matlab

• Программист должен знать о случаях использования, например, когда Matlab выполняет вычисления на месте.
• Используйте гибкую индексацию при работе с таблицами
• Напишите функции Matlab с гибким синтаксисом вызова