В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Код
X = np . array ( [ [ 0 , 0 , 1 ] , [ 0 , 1 , 1 ] , [ 1 , 0 , 1 ] , [ 1 , 1 , 1 ] ] )
y = np . array ( [ [ 0 , 1 , 1 , 0 ] ] ) . T
syn0 = 2 * np . random . random ( ( 3 , 4 ) ) — 1
syn1 = 2 * np . random . random ( ( 4 , 1 ) ) — 1
for j in xrange ( 60000 ) :
l1 = 1 / ( 1 + np . exp ( — ( np . dot ( X , syn0 ) ) ) )
l2 = 1 / ( 1 + np . exp ( — ( np . dot ( l1 , syn1 ) ) ) )
l2_delta = ( y — l2 ) * ( l2 * ( 1 — l2 ) )
l1_delta = l2_delta . dot ( syn1 . T ) * ( l1 * ( 1 — l1 ) )
syn1 += l1 . T . dot ( l2_delta )
syn0 += X . T . dot ( l1_delta )
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Распознавание лиц на Python | Определение возраста, эмоций и расы по фотографии лица
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np
def nonlin ( x , deriv = False ) :
if ( deriv == True ) :
return f ( x ) * ( 1 — f ( x ) )
return 1 / ( 1 + np . exp ( — x ) )
# набор входных данных
X = np . array ( [ [ 0 , 0 , 1 ] ,
# выходные данные
y = np . array ( [ [ 0 , 0 , 1 , 1 ] ] ) . T
# сделаем случайные числа более определёнными
np . random . seed ( 1 )
# инициализируем веса случайным образом со средним 0
syn0 = 2 * np . random . random ( ( 3 , 1 ) ) — 1
for iter in xrange ( 10000 ) :
# прямое распространение
l1 = nonlin ( np . dot ( l0 , syn0 ) )
# насколько мы ошиблись?
l1_error = y — l1
# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin ( l1 , True ) # .
# обновим веса
syn0 += np . dot ( l0 . T , l1_delta ) # .
print «Выходные данные после тренировки:»
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
НЕЙРОСЕТЬ своими руками за 10 минут на Python
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена . )
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена . )
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin ( x , deriv = False ) :
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
if ( deriv == True ) :
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np . array ( [ [ 0 , 0 , 1 ] , …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np . array ( [ [ 0 , 0 , 1 , 1 ] ] ) . T
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np . random . seed ( 1 )
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2 * np . random . random ( ( 3 , 1 ) ) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных.
Мы их не храним. Всё обучение хранится в syn0.
for iter in xrange ( 10000 ) :
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin ( np . dot ( l0 , syn0 ) )
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
( 4 x 3 ) dot ( 3 x 1 ) = ( 4 x 1 )
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Простейшая нейронная сеть на Python
В этой статье мы рассмотрим, как создать собственную простейшую нейронную сеть с помощью языка программирования «Питон». Мы не только создадим нейронную сеть с нуля, но и не будем использовать никаких библиотек. И займёт это всё не более девяти строчек кода на «Питоне».
Вот как выглядит код простейшей нейронной сети на «Питоне»:
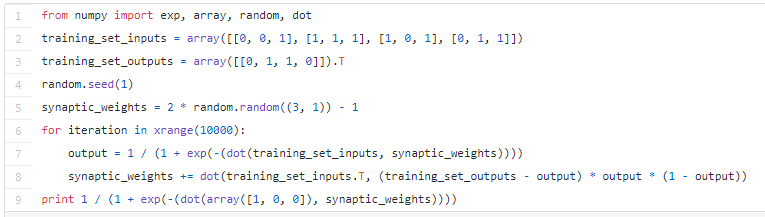
Теперь давайте поговорим о том, как это получилось, а также посмотрим на расширенную версию кода. Внимательно изучив эту статью, вы сможете и сами написать свою нейронную сеть на «Питоне».
Что такое нейронная сеть (Neural Network)?
Прежде чем продолжить, вспомним, что из себя представляет нейронная сеть. Мы знаем, что мозг человека состоит из 100 млрд. клеток, которые мы называем нейроны. Они соединены синапсами, а когда нужное количество синаптических входов возбуждено, нейрон тоже возбуждается. Этот процесс учёные называют «мышлением».

Процесс можно смоделировать, если создать нейронную сеть на ПК. Причём нет необходимости моделировать сложнейшую модель мозга человека полностью, хватит лишь нескольких основных правил. Чтобы упростить реализацию, будем использовать классические матрицы и создадим модель из 3-х входных и одного выходного сигналов. И попробуем выполнить тренировку нейрона.
Первые 4 примера — это тренировочная выборка.
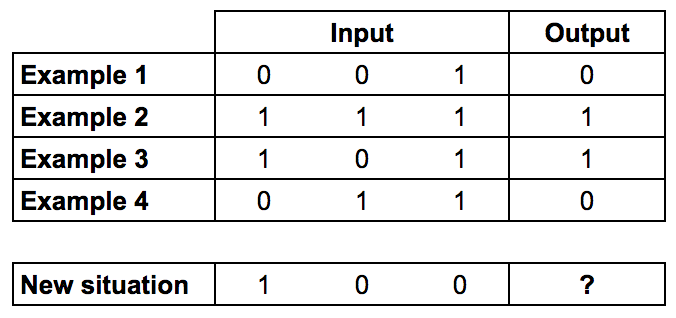
Обратите внимание, что значение столбца Output всегда равно значению самой левой колонки из столбца Input. Это значит, что правильный ответ в нашем случае будет равен 1.
Обучаем нейронную сеть
Теперь давайте добавим каждому входу вес (положительное или отрицательное число). Вход с большим отрицательным либо большим положительным весом существенно повлияет на выход нейрона. Но до начала обучения надо установить каждый вес случайной величиной.
После этого можно приступать: 1. Возьмём входные данные из примера, скорректируем значения по весам и передадим их по формуле расчёта выхода нейрона. 2. Вычислим ошибочное значение (это, по сути, разница между выходом нейрона и желаемым нами выходом в примере используемого нами тренировочного набора). 3. Немного отрегулируем вес с учётом направления ошибки. 4. Повторим данный процесс десять тысяч раз.
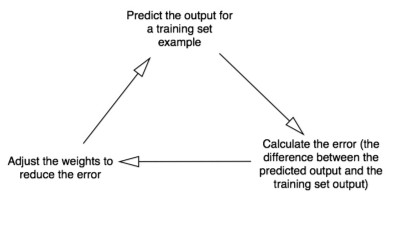
По итогу вес нейрона достигает оптимального значения для нашего обучающего набора. Теперь, если позволить нейрону «подумать», он сделает хороший прогноз.
Формулируем расчёт выхода нейрона
Теперь посмотрим на формулу расчёта выхода нейрона. Поначалу возьмём взвешенную сумму входов:
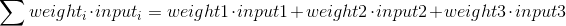
Потом выполним нормализацию, и результат будет между 0 и 1. Теперь задействуем математическую функцию Sigmoid:
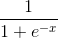
Функция Sigmoid нарисует S-образную кривую:
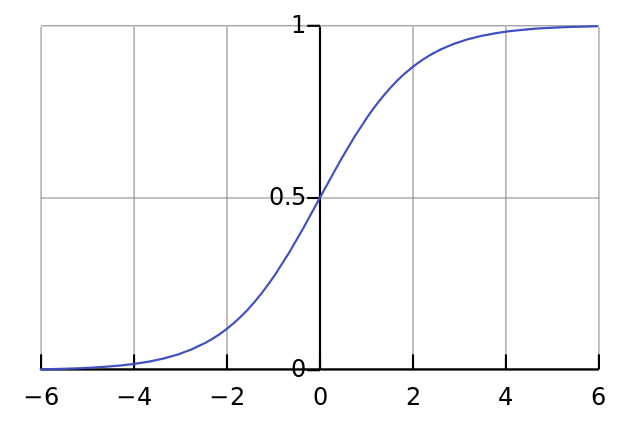
Подставим 1-е уравнение во 2-е и получим интересующую нас формулу выхода:
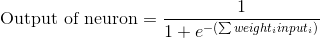
Правда, пороговый потенциал использовать не будем в целях упрощения примера.
Формула корректировки веса
В процессе тренировочного цикла мы выполняем корректировку весов. Но насколько происходит корректировка? Тут подойдёт формула взвешенной ошибки:
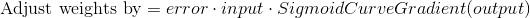
Формула позволяет выполнять корректировку пропорционально величине ошибки. Также умножение происходит на входное значение, равное 0 либо 1. Когда входное значение будет равно 0, вес корректироваться не будет. Дополнительно мы выполняем умножение на градиент сигмовидной кривой. Что тут нужно учесть: 1. Сигмовидная кривая использовалась для расчёта выхода нейрона. 2. При больших числах кривая имеет небольшой градиент.
Если нейрон уверен в правильности существующего веса, он не хочет корректировать его слишком сильно. Умножение на градиент кривой именно это и делает.
Градиент Сигмоды образуется, если будем выполнять расчёты взятием производной:
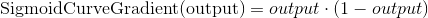
Если мы вычтем 2-е уравнение из 1-го, то получим необходимую итоговую формулу:
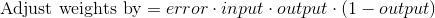
Есть и другие формулы, позволяющие нейрону обучаться быстрее, но указанная нами является максимально простой.
Пример нейронной сети на Python
Было заявлено, что библиотеки задействоваться не будут. Так-то оно так, но четыре метода из numpy импортировать придётся: — exp — для экспоненцирования; — dot — для перемножения матриц; — array — для создания матрицы; — random — для генерации случайных чисел.
Тот же array() можно применять для представления обучающего множества.

В нашем случае “.T” является функцией транспонирования матриц.
Раз мы готовы создать более красивую версию исходного кода, приступим. Обратите внимание, что на каждой итерации одновременно обрабатывается вся тренировочная выборка.
Этот код вы найдёте и по ссылке на GitHub. Если будете работать с Python 3, замените лишь xrange на range.

Итог
Давайте запустим нейронную сеть через терминал:
python main.py
Результат должен быть приблизительно следующим:

Если у вас всё получилось, поздравляем — вы только что написали простейшую нейросеть!
Смотрите, изначально нейросеть присваивала себе случайные значения весов, потом она обучалась с помощью тренировочного набора. Далее она рассмотрела новую ситуацию [1, 0, 0], предсказав 0.99993704. Так как правильный ответ равен единице, можно сказать, что предсказание получилось довольно точным.
Источник: otus.ru
Как написать простую нейросеть на Python
В последние годы нейронные сети стали одним из наиболее популярных методов для решения различных задач, таких как классификация изображений, прогнозирование временных рядов, обработка естественного языка, генерация контента и т.д. Они «умеют» извлекать признаки из данных и на основе этих признаков принимать решения, что делает их особенно полезными в сфере искусственного интеллекта.
Python является одним из самых популярных языков программирования для создания нейронных сетей, благодаря своей простоте и богатой экосистеме библиотек машинного обучения. В этой статье мы рассмотрим пошаговую инструкцию по созданию простой нейросети на Python, начиная с основных концепций нейронных сетей и заканчивая практическим созданием и обучением модели.
Основы нейронных сетей
В этом разделе мы расскажем основную информацию, связанную с нейронными сетями. А именно:
- Архитектура нейронных сетей: рассмотрим основные типы архитектур нейронных сетей, такие как перцептрон, сверточные и рекуррентные нейронные сети, а также их применение.
- Определение весов и смещений: рассмотрим, как нейронные сети извлекают признаки из входных данных, определяя веса и смещения, которые позволяют им делать выводы на основе этих признаков.
- Функции активации: рассмотрим различные функции активации, которые используются в нейронных сетях, и их роль в управлении выводом нейронов.
- Функции потерь и оптимизации: рассмотрим различные функции потерь, которые используются для измерения ошибки нейронной сети, а также различные методы оптимизации, которые используются для обновления весов и смещений нейронной сети в процессе обучения.
Архитектура нейронных сетей
Архитектура нейронных сетей описывает структуру нейронной сети и определяет, как она будет обрабатывать входные данные и выдавать выходные значения. Существует несколько типов архитектур нейронных сетей, каждый из которых предназначен для решения определенных задач.
Перцептрон
Перцептрон — это один из самых простых типов нейронных сетей, который состоит из одного или нескольких слоев нейронов. Каждый нейрон в перцептроне имеет свои веса и смещение, которые позволяют ему обрабатывать входные данные и выдавать выходные значения.
Перцептроны часто используются для задач классификации, таких как определение, является ли изображение котом или собакой.
Сверточные нейронные сети
Сверточные нейронные сети особенно хорошо подходят для обработки изображений. Они имеют несколько слоев, включая сверточные слои, пулинг слои и полносвязные слои.
Сверточные слои используются для извлечения признаков из изображений, пулинг слои уменьшают размерность выходных данных, а полносвязные слои используются для принятия окончательного решения на основе извлеченных признаков.
Рекуррентные нейронные сети
Рекуррентные нейронные сети – это тип нейронных сетей, который используется для работы с последовательными данными, такими как звуковые сигналы или текстовые данные. Рекуррентные слои в этих нейронных сетях позволяют нейронной сети запоминать информацию из предыдущих шагов и использовать ее для принятия решения на текущем шаге. Это позволяет рекуррентным нейронным сетям работать с данными разной длины и предсказывать последующие значения в последовательности.
Определение весов и смещений
Когда нейронная сеть получает на вход некоторые данные, она проходит через несколько слоев, состоящих из нейронов. Каждый нейрон обрабатывает данные и выдает некоторый результат, который передается следующему слою нейронов. Чтобы нейронная сеть могла правильно работать, ей необходимо научиться извлекать признаки из данных, то есть определять, какие входные значения наиболее важны для принятия решения.
Для этого каждый нейрон в нейронной сети имеет свой вес и смещение. Веса определяют, насколько каждый входной параметр важен для определения выхода нейрона, а смещение позволяет нейрону изменять свой выход в зависимости от входных данных.
В процессе обучения нейронная сеть корректирует значения весов и смещений таким образом, чтобы минимизировать ошибку на выходе. Для этого используются различные методы оптимизации, такие как стохастический градиентный спуск, а также различные функции потерь, которые позволяют измерить ошибку на выходе нейронной сети.
Функция активации
Функция активации играет ключевую роль в работе нейронной сети. Она применяется к выходу каждого нейрона и определяет, должен ли он быть активирован и передать свое значение на следующий слой нейронов.
Существует несколько типов функций активации, но одной из самых популярных является функция ReLU (Rectified Linear Unit). Она имеет вид f(x) = max(0, x) и позволяет нейрону передавать значение, если оно положительно, а иначе – передавать нулевое значение.
Другие функции активации, такие как сигмоида, также используются в нейронных сетях, но они менее эффективны, чем функция ReLU , особенно при работе с глубокими нейронными сетями.
При создании своей нейросети на Python необходимо выбрать подходящую функцию активации в зависимости от задачи, которую вы хотите решить. Кроме того, важно убедиться, что функция активации выбрана правильно, чтобы избежать проблем, таких как затухание градиента.
Функции потерь и оптимизация
После выбора функции активации необходимо выбрать функцию потерь, которая будет измерять ошибку нейронной сети в процессе обучения. Функция потерь должна быть выбрана в зависимости от задачи, которую вы хотите решить. Например, для задачи классификации могут быть использованы функции потерь, такие как кросс-энтропия или среднеквадратичная ошибка.
Кроме того, необходимо выбрать метод оптимизации для обучения нейронной сети. Оптимизатор используется для изменения весов нейронной сети в процессе обучения, чтобы минимизировать функцию потерь. Один из наиболее популярных оптимизаторов — это алгоритм стохастического градиентного спуска (SGD). Он обновляет веса нейронной сети в направлении, противоположном градиенту функции потерь.
Существуют и другие методы оптимизации, такие как Adam и Adagrad, которые могут быть более эффективны в некоторых случаях. При выборе оптимизатора также следует учитывать задачу и характеристики данных.
Выбор правильной функции потерь и оптимизатора — это важный шаг при создании нейронной сети. Они должны быть выбраны в соответствии с задачей и характеристиками данных, чтобы обеспечить наилучшую производительность нейронной сети.
Создание простой нейросети на Python
Рассмотрим создание простой нейросети на Python для решения определенной задачи. Возьмем таблицу с 4 столбцами: 3 из них будут входами, а последний — выходом.
Источник: timeweb.cloud