Данная спецификация требований далеко не полна, в частности, не полна спецификация пользовательского интерфейса, функциональных требований. Студентам предполагается дополнить спецификацию самостоятельно.
Часть общего описания – см. 2.1.
Калькулятор состоит из трех модулей – «Графический интерфейс», «Модуль, анализирующий и вычисляющий введенное выражение» ( AnalaizerClass.dll ) и «Модуль, реализующий математические функции» ( CalcClass.dll ). После того, как пользователь введет вычисляемое выражение одним из двух вышеописанных способов, управление передается анализирующему модулю, который форматирует выражение, выделяя числа и операторы, проверяет корректность скобочной структуры, а также выявляет неверные с точки зрения математики конструкции (например, 3+*+3 ), переводит выражение в обратную польскую запись , после чего вычисляет выражения, используя математические функции из модуля CalcClass.
- Параметры вызова (формат командной строки)
calc.exe [expression]
expression – математическое выражение, удовлетворяющее требованию 3.2
В папке с программой также находятся файлы CalcClass.dll , AnalaizerClass.dll
Вычисляем по IP с помощью Python | Как определить местоположение по IP
- Коды возврата программы.
Число и 0 на новой строке – результат вычислений выражения.
Error: <сообщение об ошибке>и код ошибки на новой строке — сообщение об ошибке в случае несоответствия входного выражения требованиям 3.2
В папке с программой также находятся файлы CalcClass.dll , AnalaizerClass.dll
Error 01 at — Неправильная скобочная структура, ошибка на символе
Error 02 at — Неизвестный оператор на символе
Error 03 — Неверная синтаксическая конструкция входного выражения
Error 04 at — Два подряд оператора на символе
Error 05 — Незаконченное выражение
Error 06 — Слишком малое или слишком большое значение числа для int . Числа должны быть в пределах от -2147483648 до 2147483647
Error 07 — Слишком длинное выражение. Максмальная длина — 65536 символов.
Error 08 — Суммарное количество чисел и операторов превышает 30
Error 09 – Ошибка деления на 0
CalcClass.dll – библиотека, в которой реализованы все необходимые математические функции.
AnalaizerClass.dll – модуль, в котором реализован синтаксический разбор выражения, а также его вычисление.
calc.exe – графическая оболочка, главный модуль.
Рис. 2.4. Интерфейс пользователя системы «Калькулятор»
Клавиши «1» «2» «3» «4» «5» «6» «7» «8» «9» «0» «/» «*» «-» «+» «mod» «(» «)» – вводят соответствующий символ в поле выражение. Клавиша «Сброс» очищает поле «Выражение», клавиша «Стереть» удаляет последний введенный символ. Клавиша «=» начинает выполнение вычислений. «MR», «M+» и «MC» управляют памятью калькулятора, «+/-» — триггер унарного плюса унарного минуса.
- Модуль математических операций ( CalcClass.dll ) Модуль содержит все математические функции, используемые в программе.
/// /// Функция сложения числа a и b /// /// слагаемое /// слагаемое /// сумма public static int Add(long a, long b) /// /// функция вычитания чисел a и b /// /// уменьшаемое /// вычитаемое /// разность public static int Sub(long a, long b) /// /// функция умножения чисел a и b /// /// множитель /// множитель /// произведение public static int Mult(long a, long b) /// /// функция нахождения частного /// /// делимое /// делитель /// частное public static int Div(long a, long b) /// /// функция деления по модулю /// /// делимое /// делитель /// остаток public static int Mod(long a, long b) /// /// унарный плюс /// /// /// public static int ABS(long a) /// /// унарный минус /// /// /// public static int IABS(long a) Используется также глобальная переменная: /// /// Последнее сообщение об ошибке /// Поле и свойство для него /// private static string _lastError = «»; public static string lastError
Листинг 2.1.
Модуль математических операций
Состоит из следующих методов и свойств:
/// /// позиция выражения, на которой отловлена синтаксическая ошибка (в случае ловли на уровне выполнения — не определяется) /// private static int erposition = 0; /// /// Входное выражение /// public static string expression = «»; /// /// Показывает, есть ли необходимость в выводе сообщений об ошибках.
В случае консольного запуска программы это значение — false. /// public static bool ShowMessage = true; /// /// Проверка корректности скобочной структуры входного выражения /// /// true — если все нормально, false — если есть ошибка /// метод бежит по входному выражению, символ за символом анализируя его и считая количество скобочек. В случае возникновения /// ошибки возвращает false, а в erposition записывает позицию, на которой возникла ошибка. public static bool CheckCurrency() /// /// Форматирует входное выражение, выставляя между операторами пробелы и удаляя лишние, а также отлавливает неопознанные операторы, следит за концом строки /// также отлавливает ошибки на конце строки /// /// конечную строку или сообщение об ошибке, начинающиеся со спец. символа https://intuit.ru/studies/courses/1040/209/lecture/5383?page=2″ target=»_blank»]intuit.ru[/mask_link]
Создать процедуру для нахождения корней квадратного уравнения по его коэффициентам a b c
Исходник программы Паскаль, которая находит корни квадратного уравнения по заданным коэффициентам
Добрый день. Сегодня я хочу поделиться программой, написанной на языке программирования Паскаль, а именно исходник программы, которая находит корни квадратного уравнения.
Итак, задача звучит следующим образом:
«Составьте программу вычисления корней квадратного уравнения по данным значениям его коэффициентов».
Решение задачи на языке паскаль довольно простое. Вначале необходимо считать данные (значения коэффициентов) в три переменные a,b,c. Затем нужно посчитать дискриминант, после проверить больше или меньше нуля или равно ему значение дискриминанта. В зависимости от значения дискриминанта считать значение корней или вывести сообщение о том, что корней нет.
Исходный код программы нахождения корней:
Скачать исходник: koren2.pas
Создать процедуру для нахождения корней квадратного уравнения по его коэффициентам a b c
Введение.
Здравствуйте. На этот раз я хотел бы предложить вам исходник программы на языке PascalABC, которая решает квадратное уравнение, строя его на считанных с клавиатуры коэффициентов.
Задача.
Перед нами поставлена задача написать программу, которая будет искать решения квадратного уравнения по заранее указанным значениям его коэффициентов. Данное решение можно считать достаточно простым, использовать мы будем цикл IF. Для выполнения задачи необходимо считать данные в соответствующее количество переменных, затем найти значение дискриминанта, проверить больше, меньше, или равен ли он нулю. Далее в зависимости от результатов проверки высчитываются и выводятся корни, либо сообщение о том, что корней нет. Для ясности понимания к каждой строке кода приложены необходимые комментарии.
Программа для решения квадратных уравнений на C++
Довольно часто в пособиях по программированию встречаются задания по нахождению решений каких-нибудь математических уравнений. Задача нахождения корней квадратного уравнения — это довольно тривиальная задача, как и многие другие задачи. Решается она очень просто при помощи листа бумаги и ручки, но решение можно автоматизировать посредством написания прикладной программы и её использования. В этой статье мы напишем такую программу.
Алгоритм решения квадратного уравнения
Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.
Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.
Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .
Существует несколько условий:
- Если D > 0, то решение имеет 2 различных вещественных корня.
- Если D = 0, то оба вещественных корня равны.
- Если D для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;
Для вас это может быть интересно:
Программа для решения квадратных уравнений на C++ : 24 комментария
- Nicknixer Автор записи 15.10.2016
Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.
Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.
Ответил вам по электронной почте
Критику принимаете?
Программа дырявая как сито.
Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.
x = ( -1*b + sqrt(b*b — 4*a*c) ) / (2 * a);
x = ( -1*b — sqrt(b*b — 4*a*c) ) / (2 * a);
Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).
Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.
Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test.
Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.
- Николай Сергейчук Автор записи 09.02.2017
Принимаем
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!
Николай, доброго времени суток! Можете помочь с написанием програмки в с++? 1-1/2!+1/3!-1/4!+1/5! и так до 1/100! ? Чтобы при заднии в строке номера члена последовательности выдавал сумму до него по такой вот формуле? Буду очень благодарен!
Пожалуйста подскажите как ввести экран правильный ответ дискриминанта
Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0
Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?
#include
using namespace std;
int main()
b;
cout <> c;
D = pow(b, 2) — 4 * a * c;
cout
ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++
Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!
помогите решить. заданы 3 перемены a.b.c записать вы радение на С
b,
b и а не равно != с
iconcerts где забыл
#include
Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2
День добрый.
Недавно начал изучать C++. Решил попробовать написать решение квадратного уравнения именно через оператор вида «условие ? выполняется : не выполняется». Т.е. если условие выполняется, то имеем два решения (даже если d = 0, то тоже должно быть два решения x1 = x2), если d a;
std::cout <> b;
std::cout <> c;
d = pow(b, 2) — 4 * a*c;
d >= 0 ? xfst = ((-b + sqrt(d)) / double(2 * a)) , xscd = ((-b — sqrt(d)) / double(2 * a)) : std::cout
- Николай Сергейчук Автор записи 12.02.2020
if (d >= 0) = 0 ) = 0) = 0, y2 >= 0)
Свежие записи
- Сера — химические свойства, получение, соединения.
- Нитрат кальция: способы получения и химические свойства
- Кальций: способы получения и химические свойства
- Гидроксид натрия: способы получения и химические свойства
- Гидроксид кальция: способы получения и химические свойства
Источник: all-equa.ru
Точка пересечения двух лучей
Вычисление точки пересечения лучей в программном коде
К статье приложена программа демонстрации вычисления точки пересечения двух лучей. Мышью и служебными клавишами можно управлять началом и направлением, создавая различные комбинации положений лучей. В исходнике содержится класс Intersections имеющий метод вычисления точки пересечения лучей на плоскости RayRay(Point r1, Point r2, Point p1, Point p2, out Point pCross, out Info info) .
Варианты пересечения двух лучей
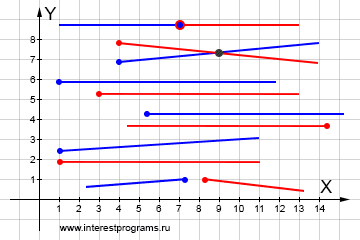
Два луча могут занимать различные положения на плоскости при которых они могут пересекаться в одной точке друг с другом, не иметь общих точек, иметь бесконечное количество общих точек.
Поскольку луч имеет начало и продолжается бесконечно только в одну сторону, то в сравнении с прямой он предлагает больше вариантов размещения в координатных системах. В случае непересечения лучей иногда практический интерес представляет мнимая точка пересечения лежащая за пределами одного или обоих лучей.
Частные случаи пересечения двух лучей. Лучи могут иметь бесконечное количество общих точек, в таком случае говорят о полном или частичном совпадении друг с другом. Лучи имеют точки начала с равными координатами.
Лучи пересекаются в одной точке
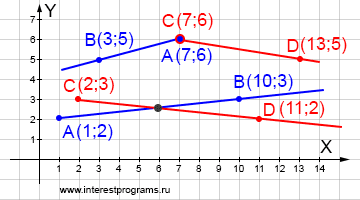
Частный случай совпадения начальных точек двух лучей позволяет получить значения общих координат «сразу», при построении лучей и без вычисления.
Для нахождения общих координат других случаев пересечения лучей в одной точке необходимы математические процедуры. Аналогично нахождению пересечения луча и прямой, для описания лучей применим параметрические уравнения.
Параметрические уравнения x = x0 + vt y = y0 + wt где v и w координаты вектора направления луча: v = x1 — x0 w = y1 — y0 t — параметр определяющий расположение точек луча точки лежат на луче при t >= 0, при t = 0 уравнения выведут координаты начала луча при t < 0, точки принадлежат мнимому продолжению луча в противоположную сторону
Создадим систему уравнений для двух лучей. 4 уравнения, 4 неизвестных — система решаема.
| x = Ax + (Bx — Ax)tab | y = Ay + (By — Ay)tab | x = Cx + (Dx — Cx)tcd | y = Cy + (Dy — Cy)tcd Если точка пересечения существует, то tab >= 0 и tcd >= 0 Для доказательства факта пересечения необходимо вычисление обоих параметров: tab и tcd.
Подставим известные значения:
| x = 1 + (10 — 1)tab | x = 1 + 9tab | y = 2 + (3 — 2)tab => | y = 2 + tab | x = 2 + (11 — 2)tcd | x = 2 + 9tcd | y = 3 + (2 — 3)tcd | y = 3 — tcd
Вычислим соотношения параметров:
вычисление через неизвестную x 1 + 9tab = 2 + 9tcd => 9tab = 1 + 9tcd => tab = tcd + 1/9
Теперь возможно вычисление значения одного параметра для подтверждения пересечения или непересечения лучей:
используем другие уравнения — вычисление через неизвестную y 2 + tab = 3 — tcd => tab = 1 — tcd => tcd + 1/9 = 1 — tcd => tcd = (1 — 1/9) / 2 => tcd ≈ 0.4444 tab =0.4444 + 1/9 ≈ 0.5555 tcd > 0 и tab > 0 — лучи пересекаются
Находим координаты точки пересечения используя вычисленный параметр:
x = 2 + 9tcd => x = 2 + 9 * 0.4444 => x = 5.9996 y = 3 — tcd => y = 3 — 0.4444 => y = 2.5556
Лучи не имеют общих точек
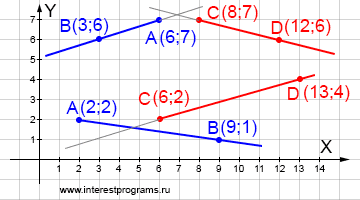
На рисунке показаны два варианта расположения лучей при которых они не пересекаются.
На одном из них мнимая точка пересечения находится за пределами обоих лучей. Другой вариант располагает мнимую точку пересечения на одном из лучей.
Для доказательства непересечения лучей также используем параметрические уравнения описанные выше. Если хотя бы один параметр имеет отрицательное значение — значит лучи не имеют общих точек.
x = x0 + vt y = y0 + wt
Докажем для первого случая, что лучи не пересекаются. Напишем систему уравнений для двух лучей:
| x = Ax + (Bx — Ax)tab | y = Ay + (By — Ay)tab | x = Cx + (Dx — Cx)tcd | y = Cy + (Dy — Cy)tcd если лучи не пересекаются, то при tab < 0 и tcd < 0 мнимая точка пересечения не лежит ни на одном луче, при tab < 0 или tcd < 0 мнимая точка пересечения принадлежит одному из лучей, у которого параметр t >0. При получении первого t < 0 вычисление второго имеет только статистический смысл, так как отрицательный первый параметр уже доказывает что лучи не имеют общих точек.
Подставим значения известных координат точек лучей:
| x = 6 + (3 — 6)tab | x = 6 — 3tab (у.1) | y = 7 + (6 — 7)tab => | y = 7 — tab (у.2) | x = 8 + (12 — 8)tcd | x = 8 + 4tcd (у.3) | y = 7 + (6 — 7)tcd | y = 7 — tcd (у.4)
Через переменную x найдем соотношение параметра первого луча к параметру второго луча:
6 — 3tab = 8 + 4tcd => -3tab = 2 + 4tcd => tab = (-2 — 4tcd) / 3,
Теперь мы можем получить значения параметров лучей:
искать будем через переменную y 7 — tab = 7 — tcd => tab = tcd => (у.5) (-2 — 4tcd) / 3 = tcd => tcd = -2/7 из уравнения (у.5) получаем значение второго параметра tab = tcd (т.1) => tab = -2/7
Оба параметра имеют отрицательные значения, лучи не пересекаются — мнимая точка пересечения лежит за пределами обоих лучей. Подставив в уравнения лучей найденные параметры найдем координаты мнимой точки пересечения:
x = 6 — 3tab (у.1) => x = 6 — 3(-2/7) = 6 + 6/7 = 48/7 => x = 6,857 y = 7 — tab (у.2) => y = 7 — (-2/7) = 51/7 => y = 7,2857
Произведём вычисления для второго случая расположения лучей на плоскости:
| x = 2 + (9 — 2)tab | x = 2 + 7tab | y = 2 + (1 — 2)tab => | y = 2 — tab | x = 6 + (13 — 6)tcd | x = 6 + 7tcd | y = 2 + (4 — 2)tcd | y = 2 + 2tcd
Вычислим соотношение параметров лучей:
2 + 7tab = 6 + 7tcd => tab = 4/7 + tcd
Получим значения параметров лучей:
2 — tab = 2 + 2tcd => — tab = 2tcd => -4/7 — tcd = 2tcd => -4/7 = 3tcd => tcd ≈ -0,1905 tab = 4/7 + tcd => tab = 0.5714 — 0,1905 => tab = 0.3809 один из параметров отрицательный — лучи не пересекаются, другой параметр положительный — мнимая точка пересечения лежит на луче AB
Вычисление точки пересечения в программный код
На основе теоретических расчётов описанных выше создан класс Intersections с методом RayRay() вычисляющим точку пересечения двух лучей. Метод выдаёт информационные сообщения о непересечении и частных случаях расположения лучей: параллельность, совпадение, неопределенность. Практическая демонстрация работы класса прикреплена к статье в виде исходника приложения с графикой из двух лучей на плоскости.
Расположение лучей устанавливаются действиями кнопки мыши при нажатых специальных клавишах. Начальные точки — левые клавиши, вторые точки — правые клавиши. Положение лучей также можно настраивать путём ввода координат в соответствующие элементы редактирования.
class Intersections < // Получение точки пересечения двух лучей. public static bool RayRay(Point r1, Point r2, Point p1, Point p2, out Point pCross, out Info info) < // Оповещение о событиях пересечения или не пересечения. info = new Info(); // —— Данные лучей —— // Координаты направления вектора синего луча. double v = r2.X — r1.X; double w = r2.Y — r1.Y; // Координаты направления вектора красного луча. double v2 = p2.X — p1.X; double w2 = p2.Y — p1.Y; // —— /Данные лучей —— // —— Частные случаи не пересечения —— // Лучи должны быть определены, // совпадают начальные и конечные точки. // В данном случае выдаются только сообщения. if (v == 0 w == 0 v2 == 0 w2 == 0) < info.Id = 10; info.Message = «Лучи неопределённы»; return false; >else if (v == 0 w == 0) < info.Id = 11; info.Message = «Синий луч неопределён»; return false; >else if (v2 == 0 w2 == 0) < info.Id = 12; info.Message = «Красный луч неопределён»; return false; >// Для вычисления параллельности лучей // необходимо сравнить направления их векторов. // Вычисляем длины векторов double lenBlue = Math.Sqrt(v * v + w * w); double lenRed = Math.Sqrt(v2 * v2 + w2 * w2); // Нормализация векторов — создание единичного вектора направления. // Единичные векторы дают возможность сравнить направление лучей // без учёта расположения их определяющих точек. double x = v / lenBlue; double y = w / lenBlue; double x2 = v2 / lenRed; double y2 = w2 / lenRed; // Точность совпадения величин double. // Точность не может быть абсолютной, // можно только увеличить точность или уменьшить. double epsilon = 0.000001; // Проверка на совпадение с определенной точностью. // Совпадение — это одинаковые начальные точки и направления лучей. if (r1.X == p1.X r1.Y == p1.Y Math.Abs(x — x2) < epsilon Math.Abs(y — y2) < epsilon) < info.Id = 20; info.Message = «Лучи совпадают»; return false; >// Проверка на параллельность с определенной точностью. // Параллельность — совпадение только направления лучей. if (Math.Abs(x — x2) < epsilon Math.Abs(y — y2) < epsilon) < info.Id = 21; info.Message = «Лучи параллельны»; return false; >// —— /Частные случаи не пересечения —— // —— Вычисление точки пересечения —— // Проверка факта пересечения // x = p1.X + v2t2 // y = p1.Y + w2t2 // r1.X + vt = p1.X + v2t2 => vt = p1.X — r1.X + v2t2 => // t = (p1.X — r1.X + v2t2) / v — (у.1) соотношение t-параметров // // Подробнейшее вычисление одного параметра с заменой соотношением другого // r1.Y + wt = p1.Y + w2t2 => wt = p1.Y — r1.Y + w2t2 => t = (p1.Y — r1.Y + w2t2) / w // (p1.X — r1.X + v2t2) / v = (p1.Y — r1.Y + w2t2) / w => // (p1.X — r1.X + v2t2) * w = (p1.Y — r1.Y + w2t2) * v => // w * p1.X — w * r1.X + w * v2t2 = v * p1.Y — v * r1.Y + v * w2t2 => // w * v2t2 — v * w2t2 = -w * p1.X + w * r1.X + v * p1.Y — v * r1.Y => // (w * v2 — v * w2) * t2 = -w * p1.X + w * r1.X + v * p1.Y — v * r1.Y => // Получение значения одного параметра путём подстановки // вычисленного соотношения (у.1)*** // t2 = (-w * p1.X + w * r1.X + v * p1.Y — v * r1.Y) / (w * v2 — v * w2) — (у.2) double t2 = (-w * p1.X + w * r1.X + v * p1.Y — v * r1.Y) / (w * v2 — v * w2); // t = (p1.X — r1.X + v2t2) / v — (у.1) double t = (p1.X — r1.X + v2 * t2) / v; // Если один из параметров меньше 0, значит пересечения нет. if (t < 0 || t2 < 0) < info.Id = 20; info.Message = «Пересечения нет»; return false; >// Координаты точки пересечения pCross.X = p1.X + v2 * t2; pCross.Y = p1.Y + w2 * t2; info.Id = 0; info.Message = «Пересечение есть»; return true; // —— /Вычисление точки пересечения —— > > public class Info < // Для визуального сообщения. public string Message; // Для автоматических действий. public int Id; >
Исходник приложения нахождения точки пересечения лучей на плоскости
Исходный код написан в среде MS Visual Studio 2022, .NET6. В составе исходника скомпилированное приложение для нахождения точки пересечения лучей без открытия решения.
Источник: www.interestprograms.ru