Алгоритм является точным математическим понятием. В качестве формальной модели алгоритма исторически первой была модель машины, предложенная англичанином Аланом Тьюрингом в 40-х годах 20-го века. Именно машины Тьюринга получили наибольшее распространение в теоретической математике при изучении свойств алгоритмов. Прежде всего, машины Тьюринга позволили решить многие важные вопросы, связанные с проблемой алгоритмической разрешимости или неразрешимости той или иной проблемы. К этому вопросу мы обратимся несколько ниже.
Машина Тьюринга представляет собой устройство, содержащее пишущую ленту бесконечной длины, разбитую на ячейки Я1, Я2, …, Яn,… . В каждой ячейке может быть записан один и только один символ из входного алфавита машины Тьюринга. В дальнейшем для простоты будем рассматривать алфавит, состоящий всего из двух символов: 0 и 1. При этом также рассматривается пустой “символ” (именно так следует понимать содержимое ячейки, в которой не записан ни 0, ни 1).
Пустой символ обычно обозначают как . В начальный момент на ленту записывается какое-то слово. Обычно это слово представляет собой описание некоторой задачи, на которых специализируется данная машина Тьюринга.
Машина Тьюринга. 2 часть. Решение задач.
Кроме ленты, у машины имеется читающая-пишущая головка, которая позволяется считать символ из ячейки или записать в ячейку, непосредственно находящуюся под головкой, какой-то один символ. Машина Тьюринга работает по тактам. Такты машины Тьюринга никак не привязываются к единицам времени, например, секундам. Но именно в тактах измеряется “время”, затрачиваемое машиной Тьюринга на то, чтобы выполнить обработку входного слова. Разумно и сложность задачи связывать с числом тактов, которую необходимо затратить на Машине Тьюринга для ее решения.
Машина Тьюринга работает по определенным правилам. По своей сути такие правила однотипны и сводятся к следующему: считать символ из текущей ячейки.
По текущему состоянию машины и считанному символу определить новое состояние, в которое переходит машина, записать в ячейку новый символ и либо сдвинуть ленту на одну ячейку влево, либо сдвинуть ленту на одну ячейку вправо, либо оставить ленту в прежнем положении, после чего перейти к следующему такту. Машина завершает работу, если она попадает в конечное состояние. Такие правила удобнее всего представлять в виде таблицы. Возьмем в качестве примера следующую таблицу.
В этой таблице использованы следующие обозначения. Состояния машины Тьюринга обозначены как Q0 , Q1. Обычно начальное состояние обозначается как Q0 (и у нас также начальное состояние машины есть Q0). Состояние Q1 в нашем примере есть конечное состояние. В верхней строке записаны символы входного алфавита машины.
Таких символов три: 0, 1, . Пустой символ тоже считается символом, хотя реально не соответствует никакому символу вообще.
Рассмотрим строку Q0. Пусть в текущей ячейке записан 0. На пересечении столбца “0” и строки Q0 стоит действие машины — LQ0. Это действие следует понимать таким образом: первый символ U означает ничего в ячейку не писать. Второй символ L означает сдвинуть ленту на одну ячейку влево (вперед, иначе говоря).
Конструирование машины Тьюринга
Третий символ Q0 означает, в какое состояние машина переходит (в нашем случае машина остается в старом состоянии, ячейку не изменяет и сдвигает ленту вперед). Рассмотрим теперь столбец 1. Действие теперь таково 0LQ0. По этому действию в текущую ячейку будет записан 0 вместо 1; все остальное – как и в предыдущем примере. Наконец, последнее действие: UUQ1.
Это действие надо понимать так: ничего в ячейку не писать (первое U), ленту не сдвигать (второе U), перейти в конечное состояние Q1 . Вот, собственно, и все. Теперь можно догадаться, что представленная выше машина Тьюринга обнуляет числа, т.е. просто заменяет 1 на 0. Конечно, это очень элементарная машина. Но надо сразу оговориться, что решать реальные задачи на машине Тьюринга никто не будет. Машина Тьюринга используется для анализа алгоритмов. Например, вопрос типа :”Можно ли решить эту задачу?” есть по сути вопрос “Можно ли для этой задачи построить машину Тьюринга?”
Нумерация машин Тьюринга и универсальная машина Тьюринга.
Для формального анализа различных проблем, связанных с машинами Тьюринга, удобно каждой машине присвоить числовой номер – целое положительное число. Такую нумерацию можно задать разными способами. Одним из известных способов является способ К.Геделя – австрийского математика, доказавшего несколько знаменитых теорем в области логики, теории множеств и теории вычислений. Способ Геделя основан на том, что, как известно из арифметики, любое целое положительное число A можно единственным способом представить в виде произведения простых множителей в виде:
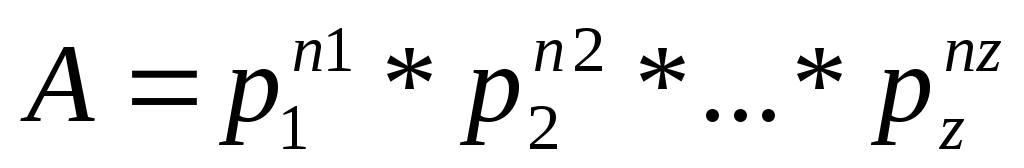
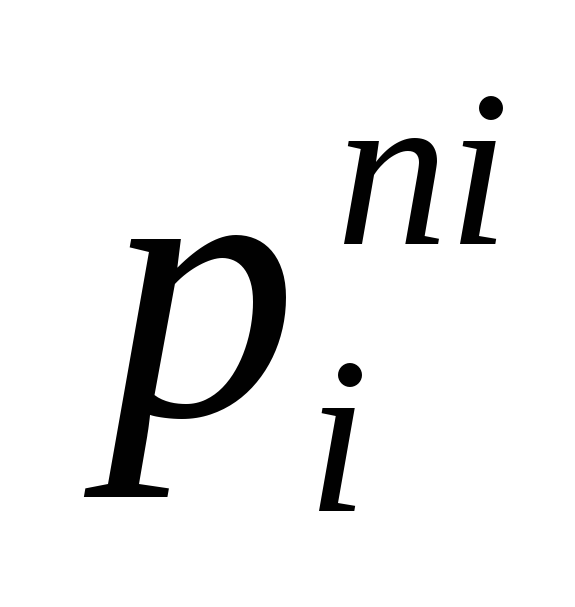
Здесь -i-й простой множитель числа А; ni – степень, с которой данный множитель входит в разложение числа А. Пример
126=2 1 * 3 2 *7 1 .
Ясно, что порядок множителей в разложении числа значения не имеет. Теперь посмотрим, как получить геделевский номер машины Тьюринга. Такая машина задана своими правилами. Каждое правило можно представить как строку символов
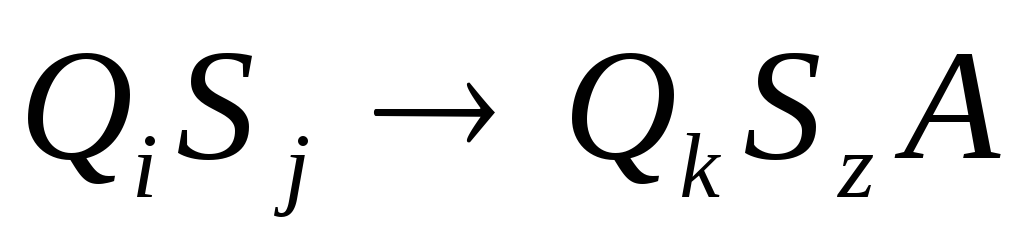
IX Международная студенческая научная конференция Студенческий научный форум — 2017


Введение. Машины Тьюринга являются важным элементом в изучении курса математической логики и теории алгоритмов. Машина Тьюринга дает один из путей уточнения понятия алгоритма. Известен тезис Тьюринга: «Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга».
Многие пытаются опровергнуть эту гипотезу – ищут пример алгоритма, который не может быть реализован с помощью тьюринговой функциональной схемы. Однако на данный момент опровергнуть гипотезу никому не удалось.
Цель работы: разработать методические материалы для студентов по теме «Машины Тьюринга» для изучения курса теории алгоритмов.
Данные материалы полезны при первоначальном знакомстве с понятием машины Тьюринга. Теоретический материал изложен очень лаконично и поэтому будет понятен любому человеку, желающему расширить свой кругозор. Тема раскрывается посредством многообразия примеров и задач со схематическим изображением.
Основные понятия. Машины Тьюринга являются одними из первых аппаратов в исследованиях по теории алгоритмов. Понятие «машин Тьюринга» было введено английским математиком и логиком Аланом Тьюрингом.
Машина Тьюрингапредставляет собой гипотетический аппарат преобразования слов. Под словом понимается произвольная последовательность символов, входящих в алфавит символов (обычно это или цифры, или начальные буквы латинского алфавита).
В состав машины Тьюринга входят: 1) бесконечная лента, разделенная на ячейки, на которой записано слово; 2) управляющее устройство, которое осуществляет преобразование слова.
В каждой ячейке записывается один символ слова. Выделяется особый пустой символ. Он заполняет все ячейки слева и справа от слова. Один из символов ленты является текущим, или, говорят, что на него указывает головка. Текущий символ можно выделять цветом или указывать на него стрелкой.
c
a
Управляющее устройство характеризуется алфавитом символов, из которых может состоять слово, и множеством состояний, в котором оно может находиться. Считается, что в алфавите символов всегда присутствует пустой символ.
Работа управляющего устройства состоит из последовательно выполняющихся тактов.
Каждый такт работы состоит в следующем: 1) чтение текущего символа ленты; 2) запись на его место нового (или, в частном случае, того же самого) символа; 3) смещение головки на одну ячейку влево, вправо или отсутствие смещения; 4) переход в новое состояние (возможно, совпадающее с текущим) или происходит останов (завершение работы).
Характеристики управляющего устройства удобно записывать в виде таблицы, в которой по строкам записываются состояния, а по столбцам символы. При этом используются следующие обозначения: R- смещение головки вправо, L- смещение головки влево, N- отсутствие смещения, ! – останов (т.е. завершение работы), q1, q2, … — состояния, ƛ – пустой символ
Пример Машины Тьюринга. Алфавит символов состоит из . Количество состояний – 2.
ƛ
a
c
q1
Источник: scienceforum.ru
Машина Тьюринга: описание и примеры машин Тьюринга
Машина Тьюринга — одно из самых интригующих и захватывающих интеллектуальных открытий 20-го века. Это простая и полезная абстрактная модель вычислений (компьютерных и цифровых), которая является достаточно общей для воплощения любой компьютерной задачи. Благодаря простому описанию и проведению математического анализа она образует фундамент теоретической информатики. Это исследование привело к более глубокому познанию цифровых компьютеров и исчислений, включая понимание того, что существуют некоторые вычислительные проблемы, не решаемые на общих пользовательских ЭВМ.

Что это и кто создал
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.

Машина Тьюринга является вычислительным устройством, состоящим из головки чтения/записи (или «сканера») с бумажной лентой, проходящей через него. Лента разделена на квадраты, каждый из которых несет одиночный символ — «0» или «1». Назначение механизма состоит в том, что он выступает и как средство для входа и выхода, и как рабочая память для хранения результатов промежуточных этапов вычислений.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
- Неограниченная лента. Она является бесконечной в обе стороны и разделена на ячейки.
- Автомат – управляемая программа, головка-сканер для считывания и записи данных. Она может находиться в каждый момент в одном из множества состояний.
Каждая машина связывает два конечных ряда данных: алфавит входящих символов A = и алфавит состояний Q = . Состояние q0 называют пассивным. Считается, что устройство заканчивает свою работу, когда попадает именно на него. Состояние q1 называют начальным — машина начинает свои вычисления, находясь на старте в нем. Входное слово располагается на ленте по одной букве подряд в каждой позиции. С обеих сторон от него располагаются только пустые ячейки.
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.

Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
- Дискретность. Цифровая машина переходит к следующему шагу n+1 только после того, как будет выполнен предыдущий. Каждый выполненный этап назначает, каким будет n+1.
- Понятность. Устройство выполняет только одно действие для одной же ячейки. Оно вписывает символ из алфавита и делает одно движение: влево или вправо.
- Детерминированность. Каждой позиции в механизме соответствует единственный вариант выполнения заданной схемы, и на каждом этапе действия и последовательность их выполнения однозначны.
- Результативность. Точный результат для каждого этапа определяет машина Тьюринга. Программа выполняет алгоритм и за конечное число шагов переходит в состояние q0.
- Массовость. Каждое устройство определено над допустимыми словами, входящими в алфавит.
Функции машины Тьюринга
В решении алгоритмов часто требуется реализация функции. В зависимости от возможности написания цепочки для вычисления, функцию называют алгоритмически разрешимой или неразрешимой. В качестве множества натуральных или рациональных чисел, слов в конечном алфавите N для машины рассматривается последовательность множества В – слова в рамках двоичного кодового алфавита В=. Также в результат вычисления учитывается «неопределенное» значение, которое возникает при «зависании» алгоритма. Для реализации функции важно наличие формального языка в конечном алфавите и решаемость задачи распознавания корректных описаний.
Программа для устройства
Программы для механизма Тьюринга оформляются таблицами, в которых первые строка и столбец содержат символы внешнего алфавита и значения возможных внутренних состояний автомата — внутренний алфавит. Табличные данные являются командами, которые воспринимает машина Тьюринга. Решение задач происходит таким образом: буква, считываемая головкой в ячейке, над которой она в данный момент находится, и внутреннее состояние головки автомата обусловливают, какую из команд необходимо выполнять. Конкретно такая команда находится на пересечении символов внешнего алфавита и внутреннего, находящихся в таблице.

Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Внешний алфавит. Это некоторое конечное множество символов, обозначающихся знаком А, составляющие элементы которого именуются буквами. Один из них — а0 — должен быть пустым. Для примера, алфавит устройства Тьюринга, работающего с двоичными числами, выглядит так: A = .
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Автоматом называется устройство, которое работает без вмешательства людей. В машине Тьюринга он имеет для решения задач несколько различных состояний и при определенно возникающих условиях перемещается из одного положения в другое. Совокупность таких состояний каретки есть внутренний алфавит. Он имеет буквенное обозначение вида Q=.
Одно из таких положений — q1 — должно являться начальным, то есть тем, что запускает программу. Еще одним необходимым элементом является состояние q0, которое является конечным, то есть тем, что завершает программу и переводит устройство в позицию остановки.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
- Запись символа внешнего алфавита в позицию, в том числе и пустого, осуществляя замену находившегося в ней, в том числе и пустого, элемента.
- Перемещение на один шаг-ячейку влево или же вправо.
- Изменение своего внутреннего состояния.
Таким образом, при написании программ для каждой пары символов либо положений необходимо точно описать три параметра: ai – элемент из выбранного алфавита A, направление сдвига каретки («←” влево, «→” вправо, «точка” — отсутствие перемещения) и qk — новое состояние устройства. К примеру, команда 1 «←” q2 имеет значение «заместить символ на 1, сдвинуть головку каретки влево на один шаг-ячейку и сделать переход в состояние q2”.
Машина Тьюринга: примеры
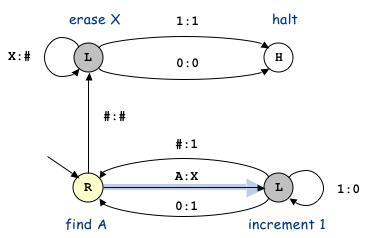
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 1 | 2 | 3 | . | 7 | 8 | 9 | ||
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | . | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
Пример 2. Дан ряд из символов, обозначающих открывающие и закрывающие скобки. Требуется построить устройство Тьюринга, которое выполняло бы удаление пары взаимных скобок, то есть элементов, расположенных подряд – “( )”. Например, исходные данные: “) ( ( ) ( ( )”, ответ должен быть таким: “) . . . ( (”. Решение: механизм, находясь в q1, анализирует крайний слева элемент в строке.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.
Источник: www.syl.ru