This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags
Nothing to show
Name already in use
A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Cancel Create
- Local
- Codespaces
HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.
Sign In Required
Please sign in to use Codespaces.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching Xcode
If nothing happens, download Xcode and try again.
Сортировка в Excel. Как сделать фильтр в excel ?
Launching Visual Studio Code
Your codespace will open once ready.
There was a problem preparing your codespace, please try again.
Latest commit
Git stats
Files
Failed to load latest commit information.
Latest commit message
Commit time
README.md
Алгоритмы сортировки на Python
Сортировка пузырьком (Bubble Sort)
Сортировка пузырьком проходит по массиву несколько раз. На каждом этапе алгоритм сравнивает два соседних элемента и, если левый элемент больше правого — меняет их местами. Такой проход гарантирует что самое больше число будет в конце массива. Этот процесс попарного сравнения повторяется до тех пор, пока каждый элемент не будет на своем месте.
def bubble_sort(arr): n = len(arr) for i in range(n): for j in range(n-i-1): if arr[j] > arr[j+1]: arr[j], arr[j+1] = arr[j+1], arr[j] return arr
Сортировка выбором (Selection Sort)
Основная идея — рассматривать последовательность как две части: первая включает отсортированные элементы, вторая — неотсортированные. Алгоритм находит наименьшее число из неотсортированной части и помещает его в конец отсортированной.
def selection_sort(arr): n = len(arr) for i in range(n-1): min_index = i for j in range(i+1, n): if arr[j] arr[min_index]: min_index = j if min_index != i: arr[i], arr[min_index] = arr[min_index], arr[i] return arr
Сортировка вставками (Insertion Sort)
Этот алгоритм совмещает идеи первых двух алгоритмов. Как и в сортировке выбором представляем последовательность как две части: первая включает отсортированные элменты, вторая — неотсортированные. Алгоритм сортировки вставками последовательно помещает каждый элемент из неотсортированной части на правильную позицию отсортированной части.
def insertion_sort(arr): n = len(arr) for i in range(1, n): current_value = arr[i] j = i — 1 while j >= 0: if current_value arr[j]: arr[j+1] = arr[j] arr[j] = current_value j = j — 1 else: break return arr
Быстрая сортировка (Quick Sort)
Сортировка данных в MS Excel
Рекурсивный алгоритм, который работает по следующему принципу:
- Выбрать опорный элемент из массива. Это можно сделать разными способами, в данной реализации этой будет случайный элемент.
- Сравнить все элементы с опорным и распределить их в подмассивы. Первый подмассив будет состоять из элементов, которые меньше опорного; второй — больше опорного или равные.
- Рекурсивно выполнить шаги 1 и 2, пока в подмассиве есть хотя бы 2 элемента.
import random def quick_sort(arr): n = len(arr) if n 1: return arr else: pivot = random.choice(arr) less = [x for x in arr if x pivot] greater_or_equal = [x for x in arr if x >= pivot] return quick_sort(less) + quick_sort(greater_or_equal)
- В худшем случае O(n²)
- В среднем случае O(n * log n)
- В лучшем случае O(n * log n)
Сортировка слиянием (Merge Sort)
Рекурсивный алгоритм, который работает по следующему принципу:
- Разделить массив на две равные части
- Отсортировать каждую половину
- Из двух отсортированных массивов получить один (операция слияния)
def merge_sort(arr): n = len(arr) if n 1: return arr else: middle = int(len(arr) / 2) left = merge_sort(arr[:middle]) right = merge_sort(arr[middle:]) return merge(left, right) def merge(left, right): result = [] while len(left) > 0 and len(right) > 0: if left[0] right[0]: result.append(left[0]) left = left[1:] else: result.append(right[0]) right = right[1:] if len(left) > 0: result += left if len(right) > 0: result += right return result
- В худшем случае O(n * log n)
- В среднем случае O(n * log n)
- В лучшем случае O(n * log n)
Источник: github.com
Методы сортировки данных. Алгоритмы поиска и сортировки
Алгоритмы сортировки данных широко используются в программировании для решения различных задач. В этой статье мы рассмотрим несколько основных алгоритмов сортировки данных в массиве.
Для начала давайте вспомним, что массив — это структура данных, которая хранит набор значений. Компоненты массива идентифицируются по индексу либо набору индексов, которые принимают целые значения из некоторого непрерывного заданного диапазона.
Но прежде чем идти дальше и говорить про алгоритмы сортировки, давайте вспомним про метод Swap . Мы введём этот метод для упрощения и улучшения читаемости кода. Он нужен, чтобы менять значения местами в массиве по индексу.
void Swap(T[] items, int left, int right) < if (left != right) < T temp = items[left]; items[left] = items[right]; items[right] = temp; >>
Что же, теперь можно приступать и к рассмотрению алгоритмов сортировки. Начнём с пузырьковой.
Пузырьковая сортировка данных
Сортировка пузырьком считается самым простым алгоритмом сортировки. В данном случае алгоритм проходит по массиву несколько раз, причём на каждом этапе происходит перемещение в конец массива самого большого из неотсортированных значений.
Представим, что у нас есть массив целых чисел:

Во время первого прохода по массиву сравниваются значения 3 и 7. Так как семь больше, всё остаётся в первоначальном виде. Далее сравниваются 7 и 4. Т. к. четыре меньше, цифры меняются местами:

В общем, процесс повторяется, пока 7 не дойдёт практически до конца. Почему практически? Потому что, как вы уже наверняка догадались, последний элемент — это 8, который больше семи, поэтому обмен не происходит. Всё чрезвычайно просто:

Однако пока обмен происходит, сортировка продолжается, в результате чего перемещается 6:

При очередном проходе обмен не выполняется, т. к. все значения массива расположены по порядку. В итоге алгоритм сортировки пузырьком заканчивает свою работу.
public void Sort(T[] items) < bool swapped; do < swapped = false; for (int i = 1; i < items.Length; i++) < if (items[i — 1].CompareTo(items[i]) >0) < Swap(items, i — 1, i); swapped = true; >> > while (swapped != false); >
Сортировка данных вставками
Эта сортировка работает путём прохождения по массиву и перемещения нужного значения в его начало. Важно помнить, что сортировка обрабатывает элементы массива по порядку. Т. к. алгоритм работает слева направо, становится очевидно, что всё, что находится слева от текущего индекса, — отсортировано. Давайте посмотрим на увеличение отсортированной части массива с каждым последующим проходом:
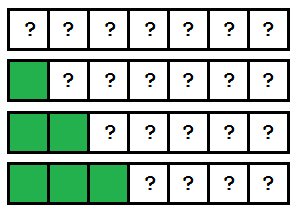
По ходу работы отсортированная часть массива растёт, таким образом, в конечном итоге, массив становится упорядоченным.
Приведём пример. Вот неотсортированный массив:

Алгоритм сортировки начнёт работать с индекса «ноль» и значения «три». Т. к. это 1-й индекс, массив до него включительно будет считаться уже отсортированным.
Потом перейдём к семёрке. Семь больше любого значения в отсортированной части, значит, осуществляется переход к последующему элементу. Отметим, что на прошедшем этапе были отсортированы компоненты с индексами 0..1, про компоненты с индексами 2..n мы пока ничего не знаем.
Теперь алгоритм проверяет четвёрку. Четыре меньше, чем 7, поэтому переносится на другую, более правильную позицию, которая находится в отсортированной части массива. Позиция определяется методом FindInsertionIndex . Метод сравнивает переданное значение (в нашем случае это 4) с каждым значением из отсортированной части и так до тех пор, пока не будет найдено место для вставки.
Так для вставки был определён индекс 1. Вставка осуществляется методом Insert . Вставляемое значение удаляется из массива, все остальные цифры сдвигаются вправо, начиная с индекса для вставки. Вот как стал выглядеть массив после сортировки:

Итог работы алгоритма сортировки вставками очевиден:

public void Sort(T[] items) < int sortedRangeEndIndex = 1; while (sortedRangeEndIndex < items.Length) < if (items[sortedRangeEndIndex].CompareTo(items[sortedRangeEndIndex — 1]) < 0) < int insertIndex = FindInsertionIndex(items, items[sortedRangeEndIndex]); Insert(items, insertIndex, sortedRangeEndIndex); >sortedRangeEndIndex++; > > private int FindInsertionIndex(T[] items, T valueToInsert) < for (int index = 0; index < items.Length; index++) < if (items[index].CompareTo(valueToInsert) >0) < return index; >> throw new InvalidOperationException(«The insertion index was not found»); > private void Insert(T[] itemArray, int indexInsertingAt, int indexInsertingFrom) < // itemArray = 0 1 2 4 5 6 3 7 // insertingAt = 3 // insertingFrom = 6 // // Действия: // 1: Сохраняем текущий индекс в temp // 2: Меняем indexInsertingAt на indexInsertingFrom // 3: Меняем indexInsertingAt на indexInsertingFrom в позиции +1 // Сдвигаем элементы влево на один. // 4: Записываем temp на позицию в массиве + 1. // Шаг 1. T temp = itemArray[indexInsertingAt]; // Шаг 2. itemArray[indexInsertingAt] = itemArray[indexInsertingFrom]; // Шаг 3. for (int current = indexInsertingFrom; current >indexInsertingAt; current—) < itemArray[current] = itemArray[current — 1]; >// Шаг 4. itemArray[indexInsertingAt + 1] = temp; >
Сортировка данных выбором
Сортировка выбором — некий гибрид между сортировкой вставками и пузырьковой сортировкой. Давайте посмотрим, как работает эта сортировка на нашем массиве:

Во время первого же прохода алгоритм посредством метода FindIndexOfSmallestFromIndex пробует найти самое меньшее значение для перемещения его в начало массива.
Так как в нашем примере массив небольшой, мы легко скажем, что это «три», да и вообще, эта цифра уже находится там, где надо. После второго прохода мы получим следующее:

И ещё после 2-х проходов алгоритм сортировки завершит работу:

public void Sort(T[] items) < int sortedRangeEnd = 0; while (sortedRangeEnd < items.Length) < int nextIndex = FindIndexOfSmallestFromIndex(items, sortedRangeEnd); Swap(items, sortedRangeEnd, nextIndex); sortedRangeEnd++; >> private int FindIndexOfSmallestFromIndex(T[] items, int sortedRangeEnd) < T currentSmallest = items[sortedRangeEnd]; int currentSmallestIndex = sortedRangeEnd; for (int i = sortedRangeEnd + 1; i < items.Length; i++) < if (currentSmallest.CompareTo(items[i]) >0) < currentSmallest = items[i]; currentSmallestIndex = i; >> return currentSmallestIndex; >
Сортировка данных слиянием
Предыдущее алгоритмы — линейные (имея квадратичную сложность, они используют мало памяти). Сортировка слиянием соответствует принципу «Divide and conquer» («разделяй и властвуй»). Она работает путём разделения крупной задачи на более мелкие, которые решаются проще.
Отвлечёмся на минутку
Представьте, что вы работаете на крыше или стройплощадке, и у вас повредился электрокабель, от которого запитывается важный инструмент. Строительные и кровельные кабели очень длинные и часто достигают 100 и более метров. Вам нужно срочно окончить работу, но у вас нет средств диагностики, чтобы починить провод.
Неопытные работники просто прекращают все действия, доложив начальству. Мастера-сдельщики режут кабель пополам, получая в 99 % случаев 50 метров работающего провода. Если нужно, они режут пополам и неработающую часть, что позволяет либо достаточно быстро найти место внешнего повреждения, внимательно изучив четверть кабеля (25 м), либо получить в итоге 75 метров, которых хватит для выполнения большинства строительных задач. Всё, что потребуется, — нож и моток изоленты.
Пример достаточно отдалённый, но всё же помогает понять, что такое сортировка слиянием. При выполнении этого алгоритма массив делится пополам до тех пор, пока каждый участок не будет иметь длину в один элемент. Далее участки сливаются (возвращаются на место), но уже в правильном порядке.
Итак, наш массив:
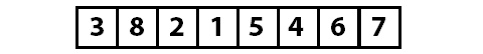
Он делится наполовину:

И потом опять, и опять наполовину:

Потом сливание/соединение в верном порядке:

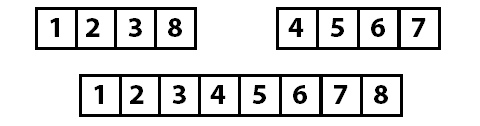
Алгоритм работает путём реализации следующих операций: 1. Рекурсивное разделение массива на группы с помощью метода Sort . 2. Слияние в верном порядке через метод Merge .
Сортировка слиянием делит и склеивает массив вне зависимости от того, был ли он изначально отсортирован либо нет. Это значит, что данный алгоритм — не самое оптимальное решение, если наш массив уже частично упорядочен и отсортирован (производительность сортировки слиянием может быть ниже, чем у линейного алгоритма).
public void Sort(T[] items) < if (items.Length int leftSize = items.Length / 2; int rightSize = items.Length — leftSize; T[] left = new T[leftSize]; T[] right = new T[rightSize]; Array.Copy(items, 0, left, 0, leftSize); Array.Copy(items, leftSize, right, 0, rightSize); Sort(left); Sort(right); Merge(items, left, right); > private void Merge(T[] items, T[] left, T[] right) < int leftIndex = 0; int rightIndex = 0; int targetIndex = 0; int remaining = left.Length + right.Length; while(remaining >0) < if (leftIndex >= left.Length) < items[targetIndex] = right[rightIndex++]; >else if (rightIndex >= right.Length) < items[targetIndex] = left[leftIndex++]; >else if (left[leftIndex].CompareTo(right[rightIndex]) < 0) < items[targetIndex] = left[leftIndex++]; >else < items[targetIndex] = right[rightIndex++]; >targetIndex++; remaining—; > >
Быстрая сортировка данных
Быстрая сортировка тоже представляет собой алгоритм, отвечающий типу «разделяй и властвуй». Сортировка данных происходит рекурсивно и поэтапно: 1. Выбирается ключевой индекс, массив делится по нему на 2 части. Выбор осуществляется разными способами, мы же возьмём случайное число.
2. Все элементы, которые больше ключевого, перемещаются в правую часть массива, которые меньше — в левую. Теперь ключевой элемент больше любого значения слева и меньше любого значения справа. 3. Первые два шага повторяются до полной сортировки массива.
Смотрим на работу алгоритма:

Выбираем ключевой элемент случайным образом:
int pivotIndex = _pivotRng.Next(left, right);

И переносим значения справа от ключевого индекса, располагая их в верном положении (используем метод partition ).

Потом повторяем этот процесс и для левой части. Рекурсивно вызываем метод quicksort для каждой из частей. Ключевым элементом слева становится пятерка — она меняет свой индекс при перемещении значений. Важно не забывать, что нас интересует в первую очередь именно ключевое значение, а не его индекс.
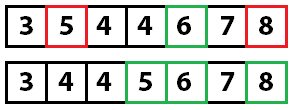
И снова быстрая сортировка:
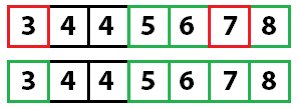
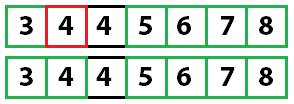
В итоге работа алгоритма завершается.
Random _pivotRng = new Random(); public void Sort(T[] items) < quicksort(items, 0, items.Length — 1); >private void quicksort(T[] items, int left, int right) < if (left < right) < int pivotIndex = _pivotRng.Next(left, right); int newPivot = partition(items, left, right, pivotIndex); quicksort(items, left, newPivot — 1); quicksort(items, newPivot + 1, right); >> private int partition(T[] items, int left, int right, int pivotIndex) < T pivotValue = items[pivotIndex]; Swap(items, pivotIndex, right); int storeIndex = left; for (int i = left; i < right; i++) < if (items[i].CompareTo(pivotValue) < 0) < Swap(items, i, storeIndex); storeIndex += 1; >> Swap(items, storeIndex, right); return storeIndex; >
Статья подготовлена специально для OTUS по материалам «Sorting Algorithms».
Хотите знать больше? Записывайтесь на курс «Алгоритмы для разработчиков»!
Источник: otus.ru
Какую сортировку можно выполнить в программе

Оранжевым отмечаются элементы, которые нужно поменять местами. Зеленые уже стоят в нужном порядке.

Наибольший элемент — число 48 — оказался в конце списка.

Наибольший элемент уже занимает место в конце массива. Чтобы поставить следующее число по убыванию, можно пройтись лишь до 4-й позиции, а не пятой.


После четвертого прохода получаем отсортированный массив.
Функция сортировки в качестве параметров будет принимать указатель на массив и его размер. Функцией swap() элементы меняются местами друг с другом:

Зеленым отмечается наименьший элемент в подмассиве — он ставится в начало списка.
Число 4 — наименьшее в оставшейся части массива. Перемещаем четверку на вторую позицию после числа 0.



Напишем функцию поиска наименьшего элемента и используем ее в сортировке:

Число 12 больше 5 — элементы меняются местами.
Проход №2. Начинаем с третьей позиции.
Проверяем вторую и третью позиции. Затем первую и вторую.

Проход №3. Начинаем с четвертой позиции.

Произошло три смены местами.
Проход №4. Начинаем с последней позиции.

Получаем отсортированный массив на выходе.

На иллюстрации массив разделяется по опорному элементу. В полученных массивах также выбираем опорный элемент и разделяем по нему.
Опорным может быть любой элемент. Мы выбираем последний в списке.
Чтобы расположить элементы большие — справа от опорного элемента, а меньшие — слева, будем двигаться от начала списка. Если число будет больше опорного, то оно ставится на его место, а сам опорный на место перед ним.


Напишем функцию разделения partition() , которая возвращает индекс опорного элемента, и используем ее в сортировке.

Цикл деления повторяется, пока не останется по одному элементу в массиве. Затем объединяем, пока не образуем полный список.
Алгоритм сортировки состоит из четырех этапов:

- Найти середину массива.
- Сортировать массив от начала до середины.
- Сортировать массив от середины до конца.
- Объединить массив.
Уменьшаем шаг в два раза. Шаг равен 2.
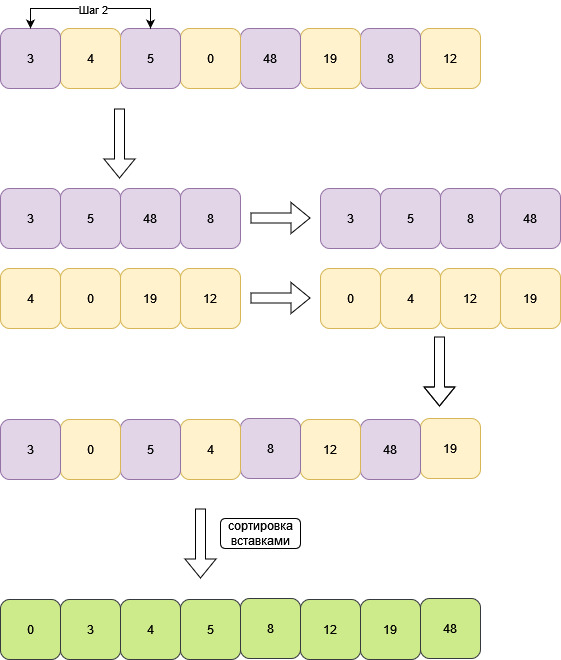

Индекс с нижним левым узлом определим по формуле n/2-1 , где n – длина массива. Получается 5/2 – 1 = 2 – 1 = 1 . С этого индекса и начинаем операцию heapify() . Сравним дочерние узлы 1-й позиции.

Дочерний узел оказался больше. Меняем местами с родителем.

Теперь проверяем родительский узел от позиции 1.

48 больше 3. Меняем местами.

После смены проверяем все дочерние узлы элемента, который опустили. То есть для числа 3 проводим heapify() . Так как 3 меньше 19, меняем местами.

Наибольший элемент оказался наверху кучи. Осталось поставить его в конце массива на позицию 4.

Теперь продолжаем сортировать кучу, но последний элемент игнорируем. Для этого просто будем считать, что длина массива уменьшилась на 1.

Повторяем алгоритм сортировки, пока куча не опустеет, и получаем отсортированный массив.
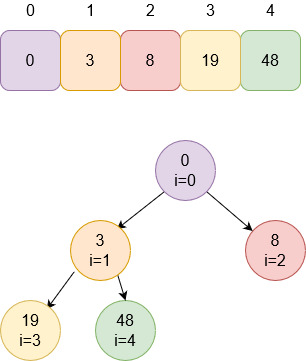
heapify.cpp
void heapify(int list[], int listLength, int root) < int largest = root; int l = 2*root + 1; int r = 2*root + 2; if (l < listLength list[l] >list[largest]) largest = l; if (r < listLength list[r] >list[largest]) largest = r; if (largest != root) < swap(list[root], list[largest]); heapify(list, listLength, largest); >>
#include using namespace std; void heapify(int list[], int listLength, int root) < int largest = root; int l = 2*root + 1; int r = 2*root + 2; if (l < listLength list[l] >list[largest]) largest = l; if (r < listLength list[r] >list[largest]) largest = r; if (largest != root) < swap(list[root], list[largest]); heapify(list, listLength, largest); >> void heapSort(int list[], int listLength) < for(int i = listLength / 2 — 1; i >= 0; i—) heapify(list, listLength, i); for(int i = listLength — 1; i >= 0; i—) < swap(list[0], list[i]); heapify(list, i, 0); >> int main() < int list[5] = ; cout
Сложность алгоритма в любом случае: O(n*logn).
В этой статье мы познакомились с семью видами сортировок, рассмотрели их выполнение и написание на С++. Попробуйте применить новые знания в решении задачек на LeetCode или Codeforces . Понимание подобных алгоритмов поможет в будущем пройти собеседование.
Материалы по теме
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Пузырьковая сортировка на JavaScript
- Вводный курс по алгоритмам: от сортировок до машины Тьюринга
Мне сложно разобраться самостоятельно, что делать?
Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- подготовитесь к техническому собеседованию и продвинутой разработке.
Курс подходит как junior, так и middle-разработчикам.
Источник: proglib.io