Какой цвет по умолчанию имеют точки привязанные к объекту в программе геогебра

В данной работе рассмотрены примеры построений в GeoGebre и плюсы и минусы программы для работы в школе.

Журавлев Евгений Валерьевич

Содержимое разработки

ФГБОУ ВО «Мордовский государственный педагогический институт имени М. Е. Евсевьева»

направление подготовки 050100.65 «Педагогическое образование»

профиль «Информатика. Математика»

Кафедра информатики и ВТ

«Построение объемных фигур и сечений в Geogebra3D»

Выполнил: студент 5 курса

группы МДИ – 112 : Журавлев Е.

Проверила: Кормилицына Т.В.

GeoGebra 3D – это свободная образовательная математическая программа, соединяющая в себе геометрию, алгебру и математические исчисления. GeoGebra 3D – свободно-распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать «живые чертежи» в планиметрии,стереометрии, в частности, для построений с помощью циркуля и линейки. Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями). Программа написана Маркусом Хохенвартером на языке Java (соответственно работает медленно,

Обозначения объектов, как их выбрать, как менять цвет, размер, как сохранить настройки. GeoGebra 5.

но на большинстве операционных систем). Переведена на 39 языков.

Полностью поддерживает русский язык.

Программная среда GeoGebra3D может быть быстро освоена людьми, имеющими элементарные навыки работы на компьютере, что, несомненно, является большим преимуществом данного программного продукта. К еще одному аргументу в пользу GeoGebra3D можно отнести её простую4 интеграцию с офисными приложениями – все чертежи легко могут через буфер обмена быть перенесены для дальнейшего использования как в текстовые редакторы, поддерживающие работу с изображениями, так и в графические редакторы.

Актуальность работы продиктована отсутствием русскоязычного раздела справки; данная квалификационная работа может претендовать на роль справочника по многим функциональным возможностям GeoGebra3D на русском языке.

Интерфейс программы.

При запуске окно программы имеет вид, приведенный на рисунке 1.

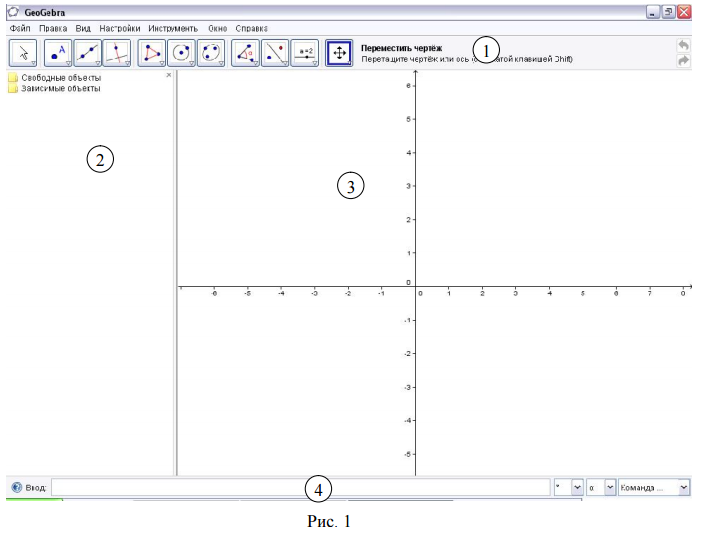
Помимо привычной для большинства программ строки меню, в окне программы расположены Панель инструментов (1), Панель объектов (2), Область геометрических построений (3) и Строка ввода (4).Для открытия полотна 3D нужно перейти в строке меню вкладку вид (Рисунок 2).

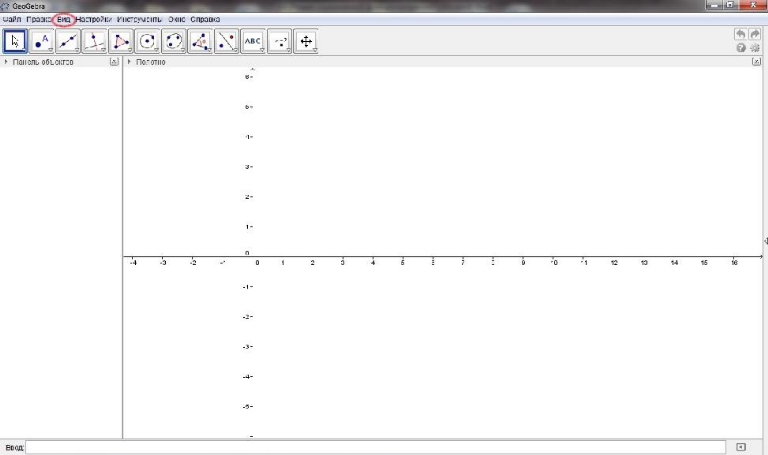
Положение свободных объектов можно изменять произвольно, тогда, как положение зависимых объектов изменяется только в соответствии с

Строка ввода состоит из двух частей: непосредственно сама Строка

ввода, а также Список команд – выпадающее меню, в котором можно

выбрать команду для ввода из списка. Отображение Списка команд можно

Инструкция по работе в программе Geogebra

отключить в меню Вид.

Отображение Панели объектов, Строки ввода можно отключить в меню Вид. В этом же меню можно включить отображение другого элемента окна программы – Таблицы. Также в меню Вид можно включить отображение на Панели объектов еще одного типа объектов – вспомогательных.

При запуске GeoGebra в области геометрических построений прорисовываются координатные оси. Также при желании можно при помощи

команды Вид – Сетка задать прорисовывание координатной сетки. Для

более подробной настройки рабочей области можно выполнить команду

Настройки – Полотно.

Здесь на вкладках Оси и Сетка можно задать цвет объектов, способы

начертания. Для осей можно указать их обозначение, указание единиц

На Панели инструментов расположены различные инструменты для

геометрических построений, разбитые на группы, о чем свидетельствует

маленький треугольник в правом нижнем углу каждой кнопки на панели.

При нажатии на него раскрывается выпадающее меню, из которого можно

выбрать нужный инструмент. При построении различных геометрических

объектов информация о них автоматически вносится в список на Панели

объектов, а сами объекты отображаются в Области геометрических построений.

Все объекты разделяются на свободные и зависимые. К свободным относятся все независимые объекты, то есть построенные произвольно в области построений. Зависимые объекты строятся, опираясь на уже имеющиеся свободные или зависимые объекты.

Для построения различных объектов используется Панель

инструментов, инструменты на которой разбиты на группы. Рассмотрим

последовательно имеющиеся в распоряжении пользователя инструменты.

При помощи инструмента Перемещать можно выбирать объекты

(группы объектов) и изменять их положение на координатной плоскости. Для

того чтобы выделить сразу несколько объектов, нужно не отпуская клавиши

Ctrl последовательно указать на них мышью.

Для построения точки нужно выбрать инструмент Точка (рис.6) и указать место на плоскости. Точка по умолчанию обозначается заглавной буквой латинского алфавита и на плоскости задается парой координат. При наведении курсора мыши на область построений он принимает вид крестика, около которого отображаются текущие координаты. Точка по умолчанию имеет синий цвет.

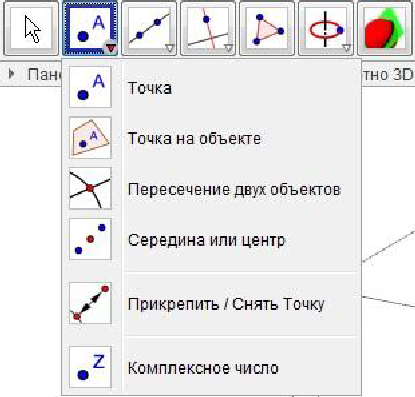
Для построения точки на каком либо объекте используется функция Точка на объекте. Выбирая этот элемент нужно помнить что точку можно поставить только на объекте, она не сможет покинуть границы объекты. Перемещать точку внутри объекта возможно. Такая точка окрашивается в синий цвет.

Для построения точек, являющихся пересечением двух объектов, можно использовать инструмент Пересечение двух объектов. Выбрав этот инструмент, нужно указать два объекта, точки пересечения которых нужно построить. Такие точки будут окрашены в серый цвет и будут являться зависимыми объектами.

Для построения середины отрезка нужно выбрать инструмент Середина или центр и указать либо две точки – концы отрезка, либо отрезок, середину которого требуется построить. При помощи того же инструмента можно построить центр геометрической фигуры, например эллипса. Для того чтобы прикрепить или снять прикрепленную точку имеется функция Прикрепить / Снять точку.

Функция Комплексное число позволяет вставлять точку на выбранную плоскость. Точка окрашивается в синий цвет. Инструменты Прямая по двум точкам, Отрезок по двум точкам, Луч по двум точкам, Вектор по двум точкам строят прямую, отрезок, луч и вектор соответственно по указанию на две точки, через которые проходит нужная линия. Можно выбирать точки, которые уже имеются на чертеже, либо указывать мышью, где будут располагаться эти точки.

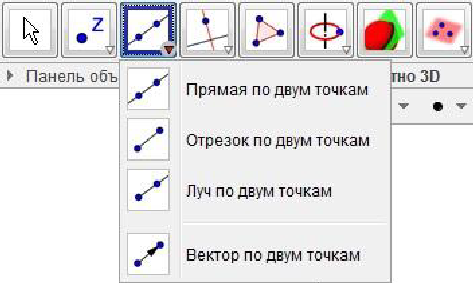
Для построения прямой, перпендикулярной данной, нужно выбрать

инструмент Перпендикулярная прямая , указать прямую на плоскости, перпендикулярная к которой будет построена, а также точку, через которую будет проходить новая прямая. Аналогичным образом строится прямая, параллельная данной, при помощи инструмента Параллельная прямая.

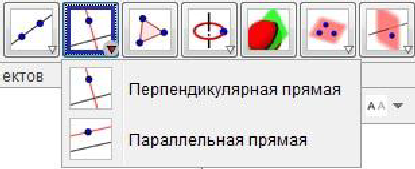
Для построения произвольного многоугольника используется инструмент Многоугольник. Для построения фигуры с его помощью необходимо последовательно указать все вершины многоугольника, а затем указать на вершину, с которой начиналось построение.

Построение объемных фигур

1. Построение призмы.

Задача. Построить призму ABCDEA1B1C1D1E1.Решение: Выбираем функцию Призма и отмечаем 5 точек на координатной оси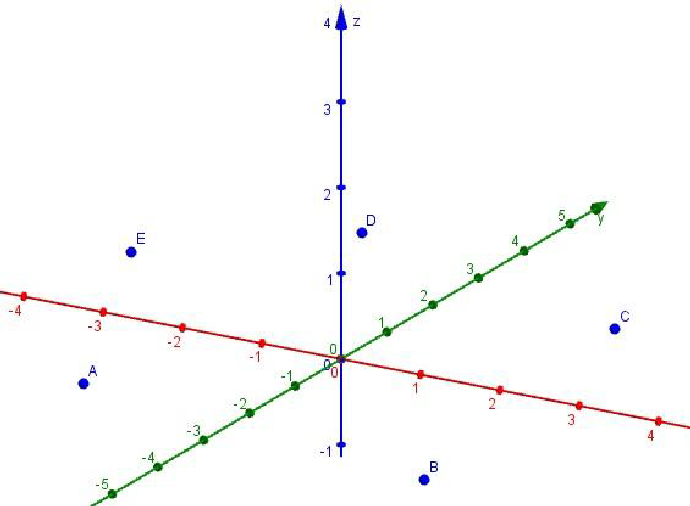
Нажимая по оси z на нужную нам высоту, получим призму ABCDEA1B1C1D1E1.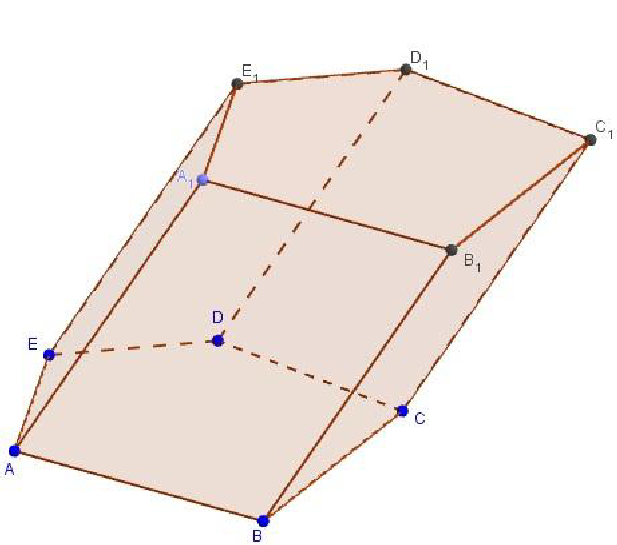

2. Построение пирамиды Задача. Построить пирамиду SABCDE. Решение: Выбираем функцию Пирамида и отмечаем 5 точек на координатной оси.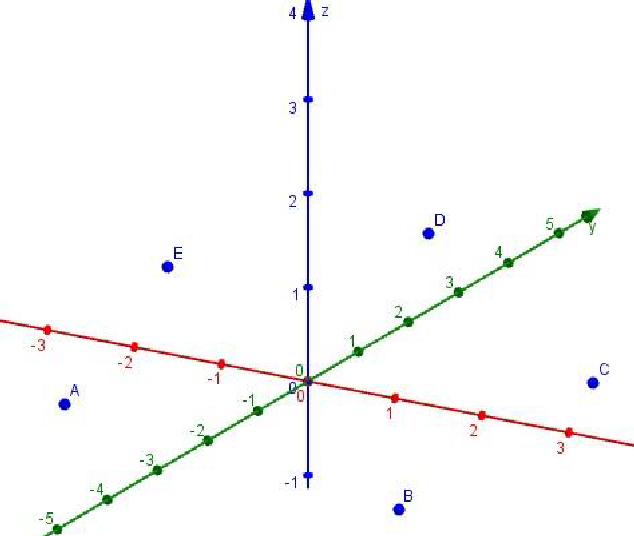

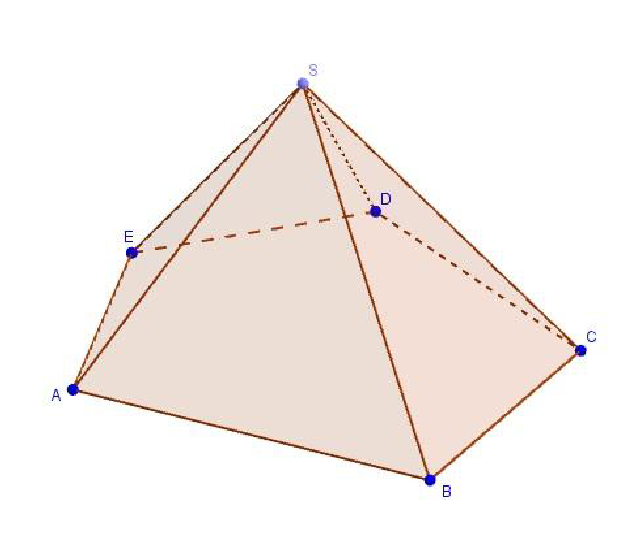Нажимая по оси z на нужную нам высоту и после переименования точки на 3.

Построение прямоугольного параллелепипеда Задача. Построить прямоугольный параллелепипед ABCDA1B1C1D1. Решение: При помощи строки ввода ставим 4 точки на плоскость XOY и одну точку на плоскость XYZ .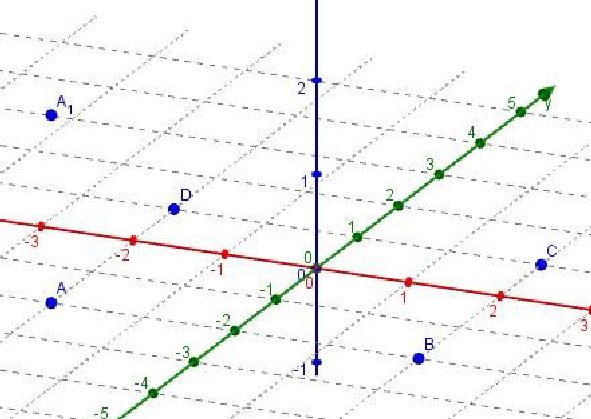
После выполнения выше указанных шагом выбираем опцию Призма соединяем точки A,B,C,D потом нажимаем на точку А и получаем прямоугольный параллелепипед ABCDA1B1C1D1. 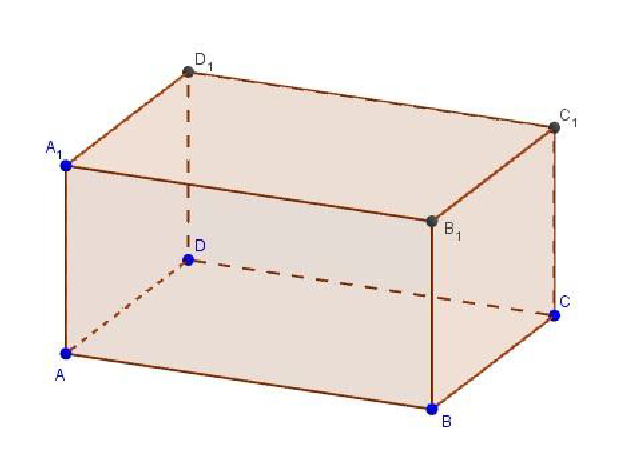4. Построение цилиндра Задача. Построить цилиндр с радиусом 2. Решение: Для построения цилиндра есть опция Цилиндр.

Выбираем эту опцию и на оси z выбираем две точки после чего выйдет окно с запросом на радиус. 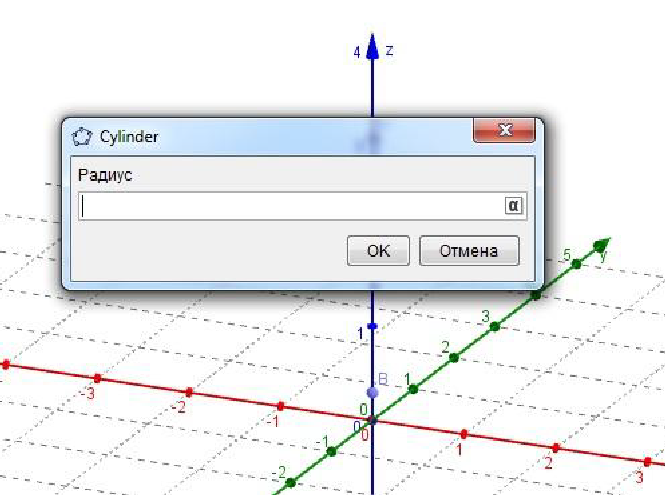Вводим значение радиуса и имеем цилиндр с данным радиусом.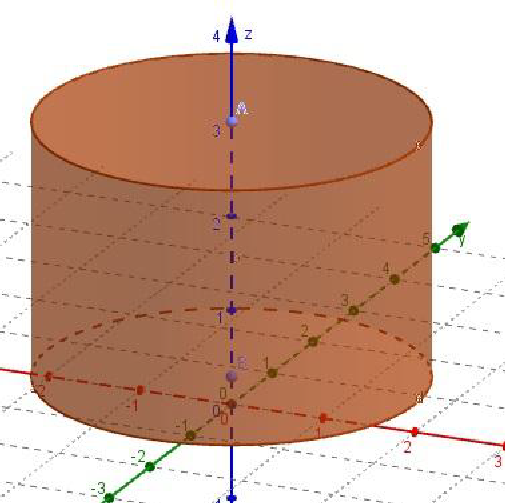

5. Построение конуса Задача. Построить конус с радиусом 3. Решение: Для построения конуса есть опция Cone. Выбираем эту опцию и на оси Z выбираем две точки после чего выйдет окно с запросом на радиус.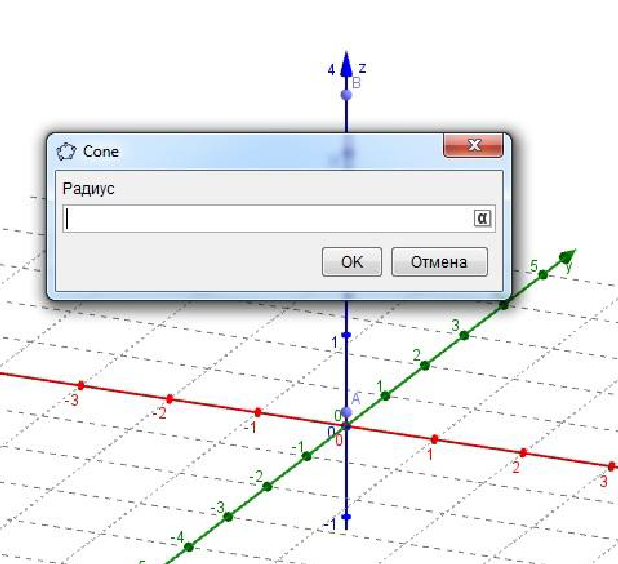

Вводим значение радиуса и имеем конус с данным радиусом.

6. Построение шара Задача. Построить шар с радиусом 3. Решение: Шар можно построить с помощью двух опций. Первая из них называется Сфера по центру и точке. При этом нужно выбрать точку центра и другую точка которой будет являться крайней точкой сфера. Вторая функция Сфера по центру и радиусу.

В этом случае нужно выбрать точку центра и выскакивает окно с запросом ввести радиус.

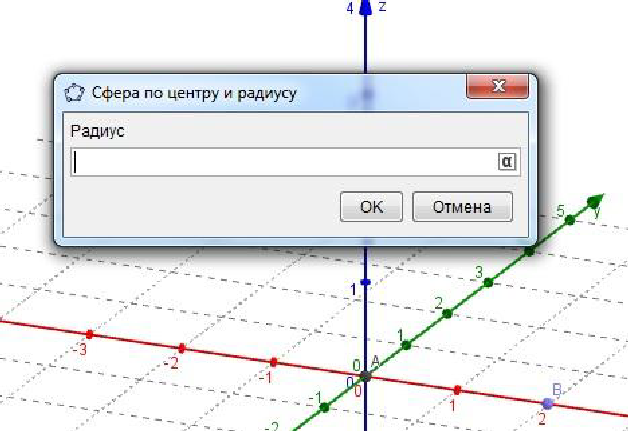
После ввода значения радиуса строиться сфера. ПОСТРОЕНИЕ СЕЧЕНИЙ 1. Построение сечения пирамиды Задача 1 На ребрах AB,BC и CD тетраэдра ABCD отмечены точки M,N и P Построить сечение тетраэдра плоскостью MNP.

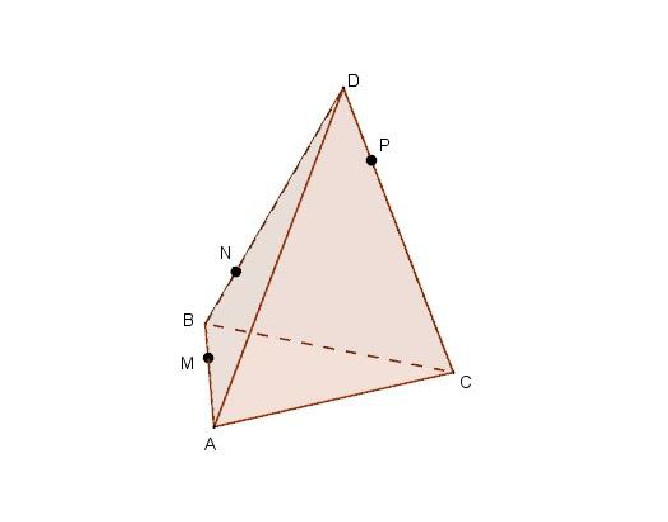Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E (рис.2), которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро AC в некоторой точке Q. Четырехугольник MN PQ – искомое сечение.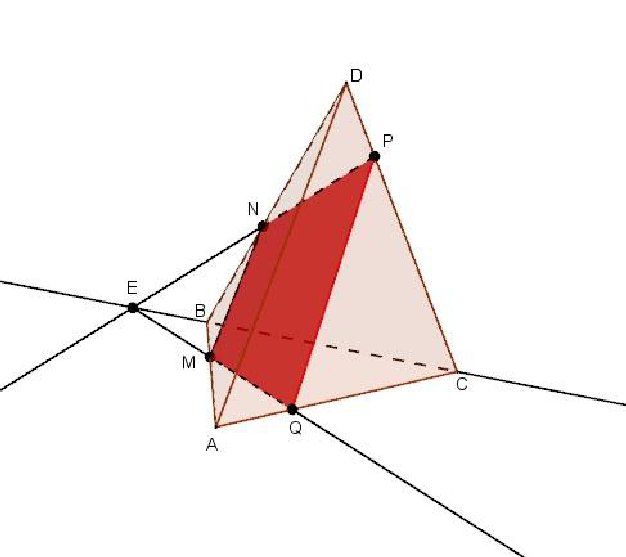
Точка M лежит на боковой грани ADB тетраэдра DABC. Построить сечение тетраэдра плоскостью, проходящей через точку M параллельно основанию ABC. Так как секущая плоскость параллельна плоскости ABC , то она параллельна прямым, AB, BC и CA. Следовательно, секущая плоскость пересекает боковые грани тетраэдра по прямым, параллельным сторонам треугольника ABC.

Отсюда вытекает следующий способ построения искомого сечения. Проведём через точку M прямую, параллельную отрезку AB, и обозначим буквами P и Q точки пересечения этой прямой с боковыми ребрами DA и DB Затем через точку P проведем прямую, параллельную отрезку AC , и обозначим буквой R точку пересечения этой прямой с ребром DC.

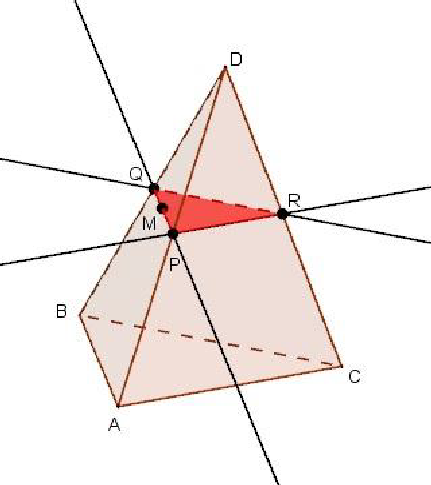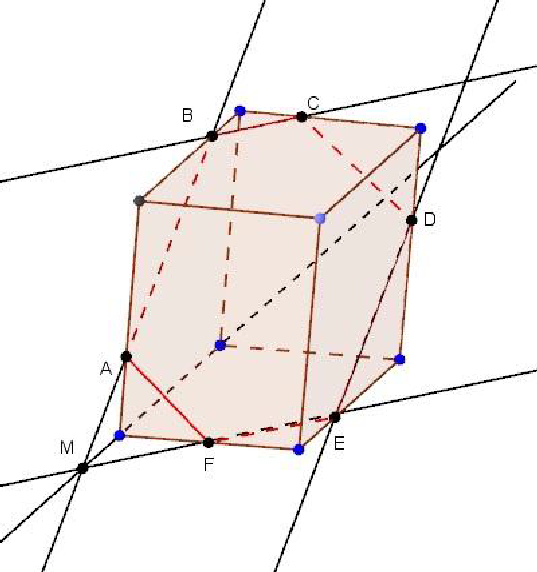
Треугольник PQR – искомое сечение. Построение сечения прямоугольного параллелепипеда Задача На ребрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC.

Решение Построение искомого сечения зависит от того, на каких ребрах параллелепипеда лежат точки A, B и C. Рассмотрим некоторые частные случаи. Если точки A,B и C лежат на ребрах, выходящих из одной вершины нужно провести отрезки AB, BC и CA, и получится искомое сечение – треугольник ABC.

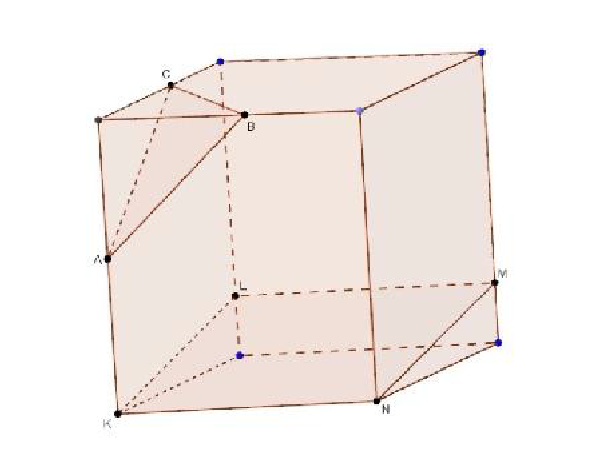
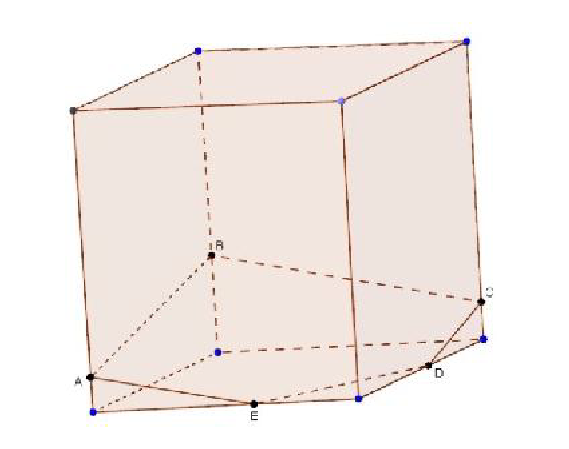
Если точки A, B и C , то сначала нужно провести отрезки AB и BC, а затем через точку A провести прямую, параллельную AB. Пересечения этих прямых с ребрами нижней грани дают точки E и D. Остается провести отрезок ED, и искомое сечение – пятиугольник ABCDE – построено.

Более трудный случай, когда данные точки A,B В этом случае можно поступить так, сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания. Для этого проведем прямую AB и продолжим нижнее ребро, лежащее в той же грани, что и прямая AB, до пересечения с этой прямой в точке M.

Далее через точку M проведем прямую, параллельную прямой BC. Это и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с ребрами нижнего основания в точках E и F. Затем через точку E проведем прямую, параллельную прямой AB.

Список использованных источников
1. Иванчук Н.В., Эйкен О.В., Мартынова Е.В., Самылова Ю.В., Данько О.Е. Использование компьютерной программы GeoGebra на уроках математики в 7-11 классах: Методическое пособие. – Мурманск: МГПУ, 2008. – 36 с. 2. Геометрия 10-11 кл. учебник для общеобразовательных учреждений. Базовый и профильный уровни. 19-е издание. Москва «просвещение» 2010. под руководством А Н Тихонова.

Авторы — Л С Атанасян, В Ф Бутузов и др. 3. Погорелов А.В. Геометрия: Учеб. Для 7-11 кл. общеобразоват. учреждений. – 9-е изд. – М.:Просвещение, 1999 4. http://www.geogebra.org/cms/ 5. http://ru.wikipedia.org/wiki/GeoGebra 6. http://www.slideshare.net/marinmets/geogebra-1962501 7. http://matematika88888.blogspot.com/2009/07/geogebra.html 8.http://shperk.ru/friends/2009/09/rukovodstvo-dlya-nachinayushhix izuchatprogrammu-geogebra/ 9. http://alexlarin.com/viewtopic.php?f=16https://videouroki.net/razrabotki/postroieniie-i-siechieniie-obiemnykh-fighur-v-geogebra.html» target=»_blank»]videouroki.net[/mask_link]

Реферат «Моделирование в Geogebra»

Помощь в организации интерактивных форм обучения высшей математике в вузе могут оказать различные математические пакеты и системы. Одной из таких систем является бесплатно распространяемая интерактивная геометрическая система GeoGebra (ИГС «GeoGebra»), обладающая просты интерфейсом пользователя и позволяющая делать геометрические построения на компьютере так, что при движении исходных объектов чертеж сохраняет свою целостность. В настоящее время идет широкое внедрение системы GeoGebra в образовательный процесс как школы, так и высших учебных заведений. Однако систему GeoGebra можно использовать не только в преподавании аналитической, дифференциальной и проективной геометрии, но и в преподавании других дисциплин, например, дискретной математики.

Появление ИГС оказывает существенное влияние на процесс обучения математики за счет возможностей наглядной визуализации и динамического моделирования математических объектов.

GeoGebra – это свободная образовательная математическая программа, соединяющая в себе геометрию, алгебру и математические исчисления. GeoGebra – свободно-распространяемая динамическая геометрическая среда, которая даёт возможность создавать «живые чертежи» в планиметрии, стереометрии, в частности, для построений с помощью циркуля и линейки.

Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, нтегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями). Программа написана Маркусом Хохенвартером на языке Java (соответственно работает медленно, но на большинстве операционных систем). Переведена на 39 языков. Полностью поддерживает русский язык.

Программная среда GeoGebra может быть быстро освоена людьми, имеющими элементарные навыки работы на компьютере, что, несомненно, является большим преимуществом данного программного продукта. К еще одному аргументу в пользу GeoGebra можно отнести её простую интеграцию с офисными приложениями – все чертежи легко могут через буфер обмена быть перенесены для дальнейшего использования как в текстовые редакторы, поддерживающие работу с изображениями, так и в графические редакторы.

1. Пользовательский интерфейс GeoGebra

После запуска GeoGebra появляется следующее окно (рис. 1): 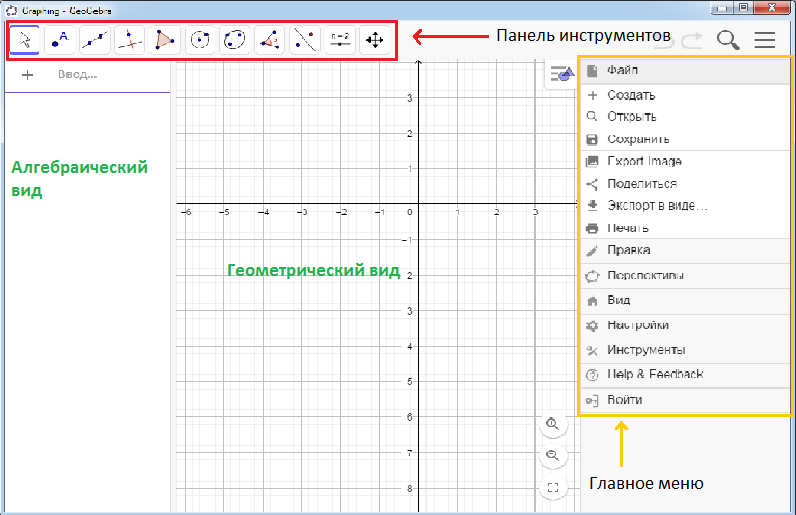Рисунок 1 Внешний вид программы Геометрические построения можно осуществить с помощью предоставленных инструментов геометрии в панели инструментов в поле «Графический вид» с помощью мыши. Так при построении прямой, проходящей через две точки, соответствующие координаты и уравнение отображаются в алгебраическом представлении (рис. 2). 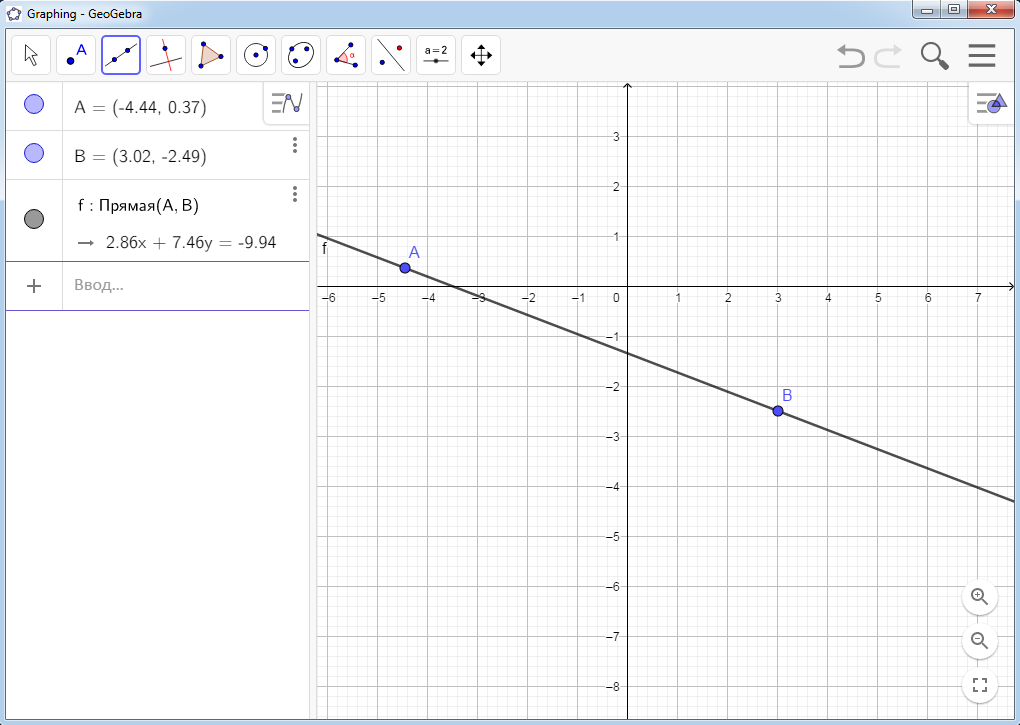Рисунок 2 Построение прямой в графическом виде Другой способ построения – это введение алгебраических данных, команд и функций в строке ввода с помощью клавиатуры, после чего графическое представление описанных объектов будет выведено в графическом виде. Кроме графического и алгебраического видов в GeoGebra также открываются такие виды как 3D, электронные таблицы, калькулятор вероятностей отобразить или скрыть которые можно, выполнив следующие действия: Главное меню – Вид (рис. 3). 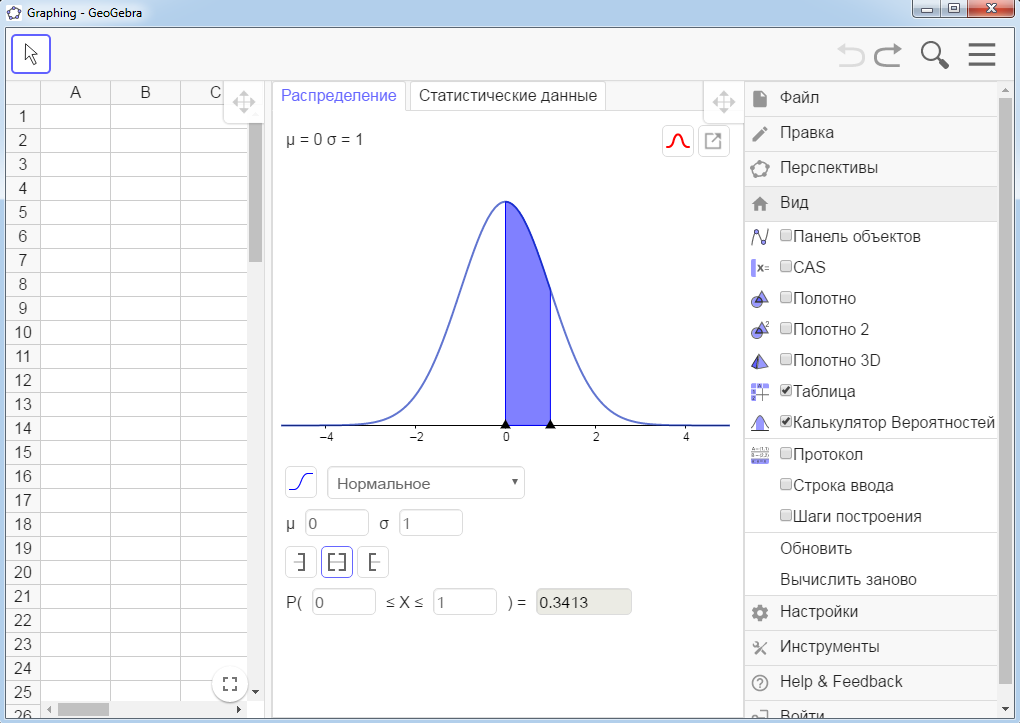Рисунок 3 Виды

1. Основы использования GeoGebra

Для открытия нового файла GeoGebra необходимо выполнить следующие действия: нажать на кнопку главного меню – выбрать пункт «Создать». Программа сразу же предлагает озаглавить файл и сохранить его (рис. 4).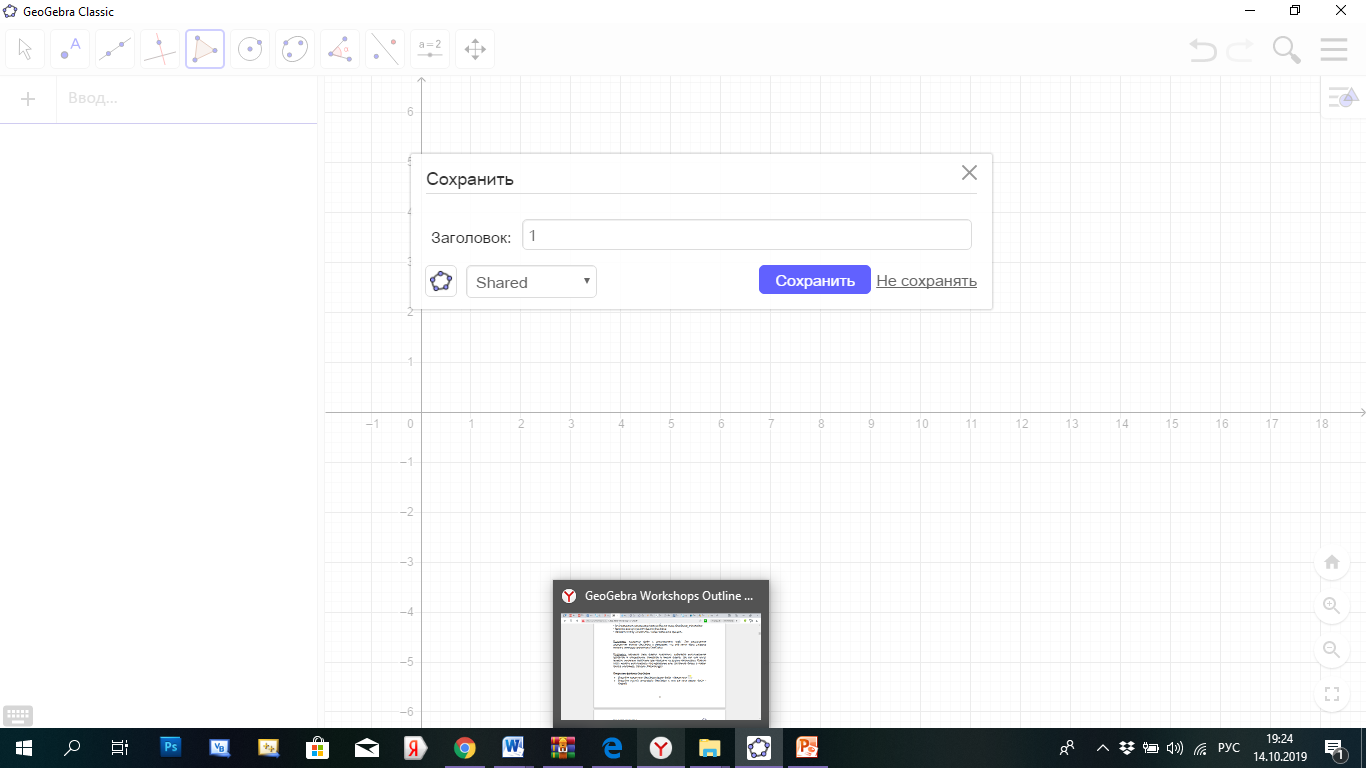

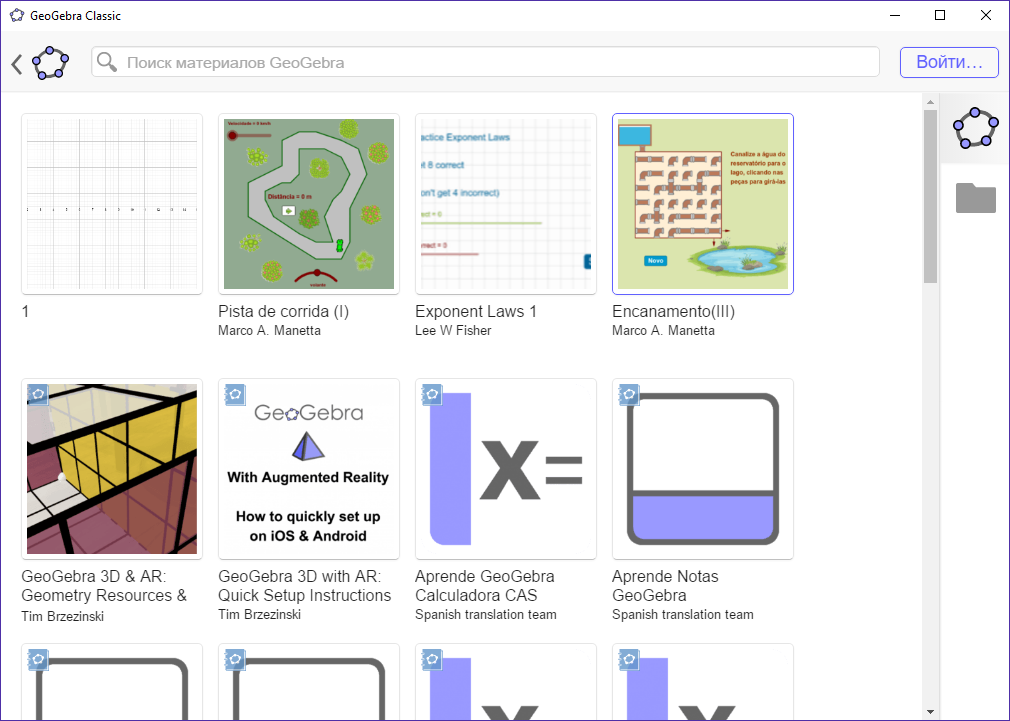Рисунок 4 Создание нового файла Создается файл с расширением .ggb, определяющим файлы GeoGebra и указывающим на тот факт, что они могут быть открыты только данной программой. Что бы открыть уже существующий файл, необходимо в пункте главного меню «Файл» выбрать команду «Открыть». Далее после нажатия на значок «Папка» (рис. 5), программа предложит выбрать путь к необходимому файлу. Необходимо выбрать файл с расширением .ggb. Рисунок 5 Открытие существующего файла Сохранение файла осуществляется по схеме: Главное меню – Файл – Сохранить. При необходимости выбрать в диалоговом окне нужную папку, в которой впоследствии будет храниться файл. Для работы с инструментами геометрии в GeoGebra необходимо: – активировать инструмент, нажав на кнопку с соответствующей иконкой; – в открывшемся под иконкой списке выбрать необходимый инструмент. Панели инструментов содержат аналогичные инструменты или инструменты, которые генерируют тот же тип нового объекта. После того как вы выбрали инструмент, программа предлагает получить справку о нем (появляется всплывающее окно внизу программы, как показано на рисунке 6). 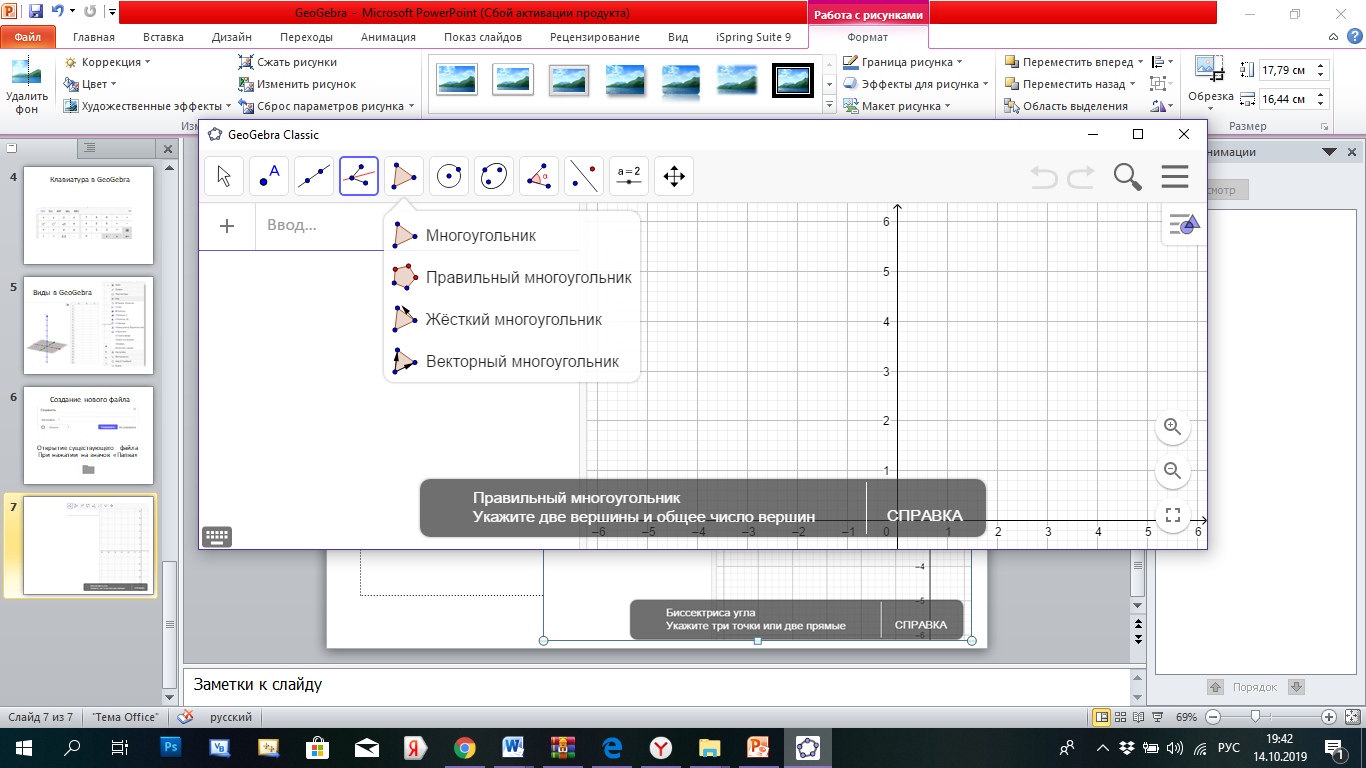Рисунок 6 Справка об инструменте 3. Использование инструментов для построений На Панели инструментов расположены различные инструменты для геометрических построений, разбитые на группы, о чем свидетельствует маленький треугольник в правом нижнем углу каждой кнопки на панели. При нажатии на него раскрывается выпадающее меню, из которого можно выбрать нужный инструмент. При построении различных геометрических объектов информация о них автоматически вносится в список на поле «Алгебраический вид», а сами объекты отображаются в поле «Геометрический вид». Все объекты разделяются на свободные и зависимые. К свободным относятся все независимые объекты, то есть построенные произвольно в области построений. Зависимые объекты строятся, опираясь на уже имеющиеся свободные или зависимые объекты. Для построения различных объектов используется Панельинструментов, инструменты на которой разбиты на группы. Рассмотрим последовательно имеющиеся в распоряжении пользователя инструменты (рис. 7). Рисунок 7 Панель инструментов При помощи инструмента Перемещать (рис. 8) можно выбирать объекты (группы объектов) и изменять их положение на координатной плоскости. Для того чтобы выделить сразу несколько объектов, нужно не отпуская клавиши Ctrl последовательно указать на них мышью, также можно выбрать «Фигура от руки», что позволит нарисовать функцию или геометрическую фигуру, а «Карандаш» дает возможность писать на полотне. 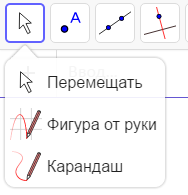Рисунок 8 Инструмент «Перемещать» Для построения точки нужно выбрать инструмент Точка (рис. 9) и указать место на плоскости. Точка по умолчанию обозначается заглавной буквой латинского алфавита и на плоскости задается парой координат. При наведении курсора мыши на поле «Геометрический вид» он принимает вид крестика, около которого отображаются текущие координаты. Точка по умолчанию имеет синий цвет. Рисунок 9 Инструмент «Точка» Для построения точки на каком-либо объекте используется функция Точка на объекте (рис. 9). Выбирая этот элемент нужно помнить, что точку можно поставить только на объекте, она не сможет покинуть границы объекты. Перемещать точку внутри объекта возможно. Такая точка окрашивается в синий цвет. Для того чтобы прикрепить или снять прикрепленную точку имеется функция Прикрепить / Снять точку (рис. 9). Для построения точек, являющихся пересечением двух объектов, можно использовать инструмент Пересечение двух объектов (рис. 9). Выбрав этот инструмент, нужно указать два объекта, точки пересечения которых нужно построить. Такие точки будут окрашены в серый цвет и будут являться зависимыми объектами. Для построения середины отрезка нужно выбрать инструмент Серединаили центр (рис. 9) и указать либо две точки – концы отрезка, либо отрезок, середину которого требуется построить. При помощи того же инструмента можно построить центр геометрической фигуры, например, эллипса. Функция Комплексное число (рис. 9) позволяет вставлять точку на выбранную плоскость. Точка окрашивается в синий цвет. Функции Extremum и Корни (рис. 9) появились недавно и воспользоваться ими пока нет возможности. Инструменты Прямая, Отрезок, Отрезок с фиксированной длиной,Луч, Ломанная, Вектор, Отложить вектор (рис.10) строят прямую, отрезок, луч, ломанную и вектор соответственно по указанию на две точки, через которые проходит нужная линия. Можно выбирать точки, которые уже имеются на чертеже, либо указывать мышью, где будут располагаться эти точки. 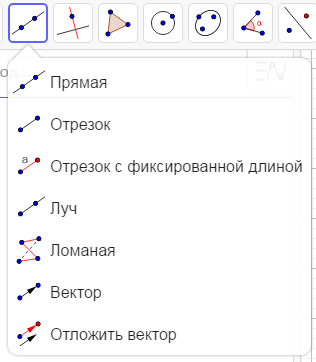Рисунок 10 Инструмент «Прямая» Для построения прямой, перпендикулярной данной, нужно выбрать инструмент Перпендикулярная прямая (рис. 11), указать прямую на плоскости, перпендикулярная к которой будет построена, а также точку, через которую будет проходить новая прямая. Аналогичным образом строится прямые, при помощи инструмента Параллельная прямая, Серединный перпендикуляр, Биссектриса угла, Касательная, Поляра или диаметр, Аппроксимация, Локус. Рисунок 11 Инструмент «Перпендикулярная прямая» Для построения произвольного многоугольника используется инструмент Многоугольник (рис. 12). Для построения фигуры с его помощью необходимо последовательно указать все вершины многоугольника, а затем указать на вершину, с которой начиналось построение. Таким же образом можно построить правильный многоугольник, жесткий многоугольник и векторный многоугольник. 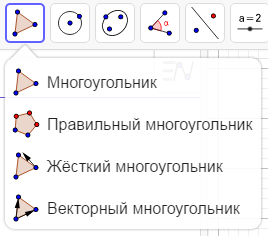Рисунок 12 Инструмент «Многоугольник» Варианты построения окружности несколько. Например, функция Окружность по центру и точке (рис. 13) позволяет построить окружность в нужной точке, но с неизвестным радиус, то есть произвольную окружность. Вторая функция данной подгруппы – Окружность по центру и радиусу (рис. 13) дает возможность построения окружность с фиксированным центром и с заданным радиусом. Для того чтобы воспользоваться данной функцией нужно мышкой указать где должен быть центр и вести размер радиуса. Функция Цикруль дает возможность указать отрезок либо две точки, задающий радиус окружности и затем центр. Следующая функция данной подгруппы делает возможным построение окружности по трем точкам на любом поверхности оси. Называется данная функция Окружность по трем точкам (рис. 13). Также можно воспользоваться инструментами: Полуокружность по двум точкам, Дуга по центру и двум точкам, Дуга по трем точкам, Сектор по центру и двум точкам, Сектор по трем точкам. 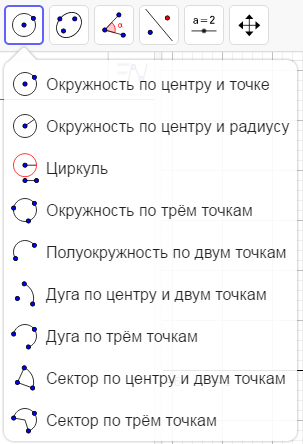Рисунок 13 Инструмент «Окружность по центру и точке» Для построения эллипса используется инструмент Эллипс (рис. 14). Кроме эллипса можно построить гиперболу – инструмент Гипербола, параболу – Парабола, конику по пяти точкам – Коника по пяти точкам. 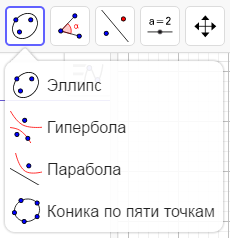Рисунок 14 Инструмент «Эллипс» Для того, чтобы построить угол нужно воспользоваться инструментом Угол (рис. 15.). Для этого необходимо выбрать три точки и две прямые. Кроме этого можно построить угол с заданной величиной – инструмент Угол заданной величины, измерить расстояние или длину – Расстояние или длина, вычислить площадь – Площадь, также воспользоваться инструментами Наклон прямой, Создать список, Отношение объектов, Исследователь функций. 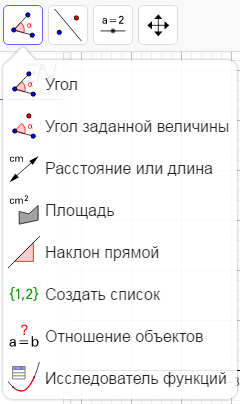Рисунок 15 Инструмент «Угол»

1. Построение чертежей в GeoGebra

Построим прямоугольник. Для того, чтобы построить прямоугольник, откроем новое окно GeoGebra. Далее следуем алгоритму построения:

1. Создадим отрезок АВ.
2. Построим перпендикулярную прямую к отрезку АВ через точку В. Для этого 2 раза щекнем по точке В.
3. Активируем точку С на перпендикулярной прямой.
4. Построим прямую, параллельную АВ, через точку С. Для этого нажмем на точку С, а затем на отрезок АВ.
5. Создадим перпендикулярную прямую к отрезку АВ через точку А. Для этого 2 раза щелкнем по точке А.
6. Построим точку пересечения D.
7. Создадим многоугольник АВСD. Для этого на панели инструментов выберем инструмент «Многоугольник» и произведем последовательные щелчки по всем точкам А, В, С, D. Что бы закрыть полигон точек, снова щелкнем по точке А.

В результате получится прямоугольник АВСD, изображенный на рисунке 16. 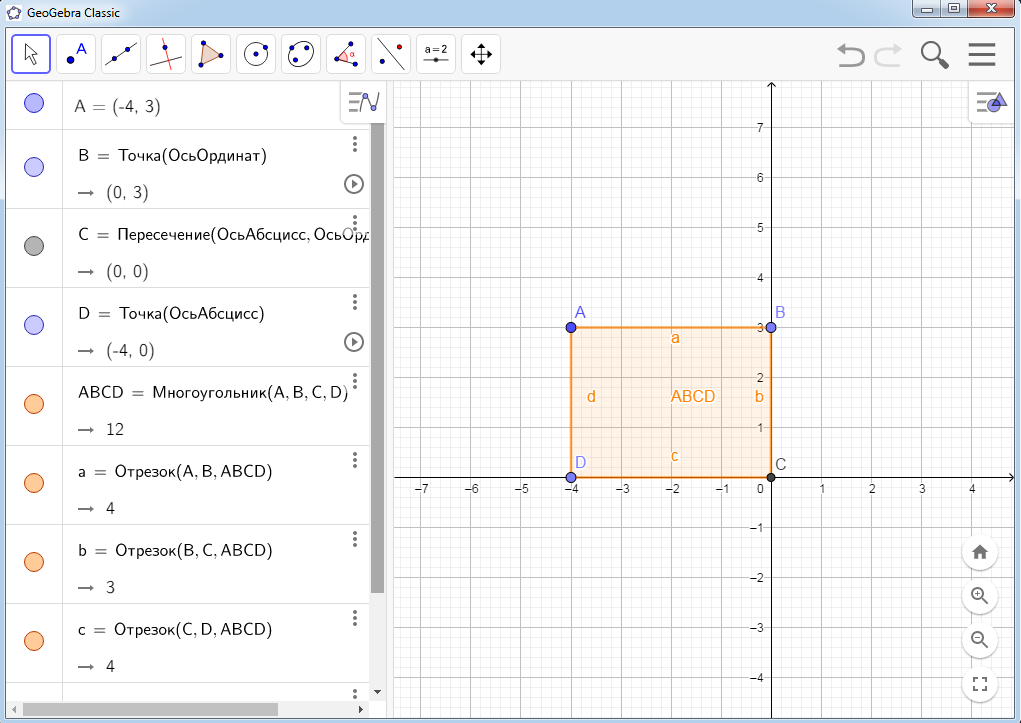Рисунок 16 Прямоугольник АВСD Программа GeoGebra позволяет просмотреть построение чертежа шаг за шагом. Для этого необходимо выполнить щелчок правой кнопкой мыши. Галочкой отметить пункт «Шаги построения» и воспроизвести построение, нажав на кнопку Play (рис. 17). 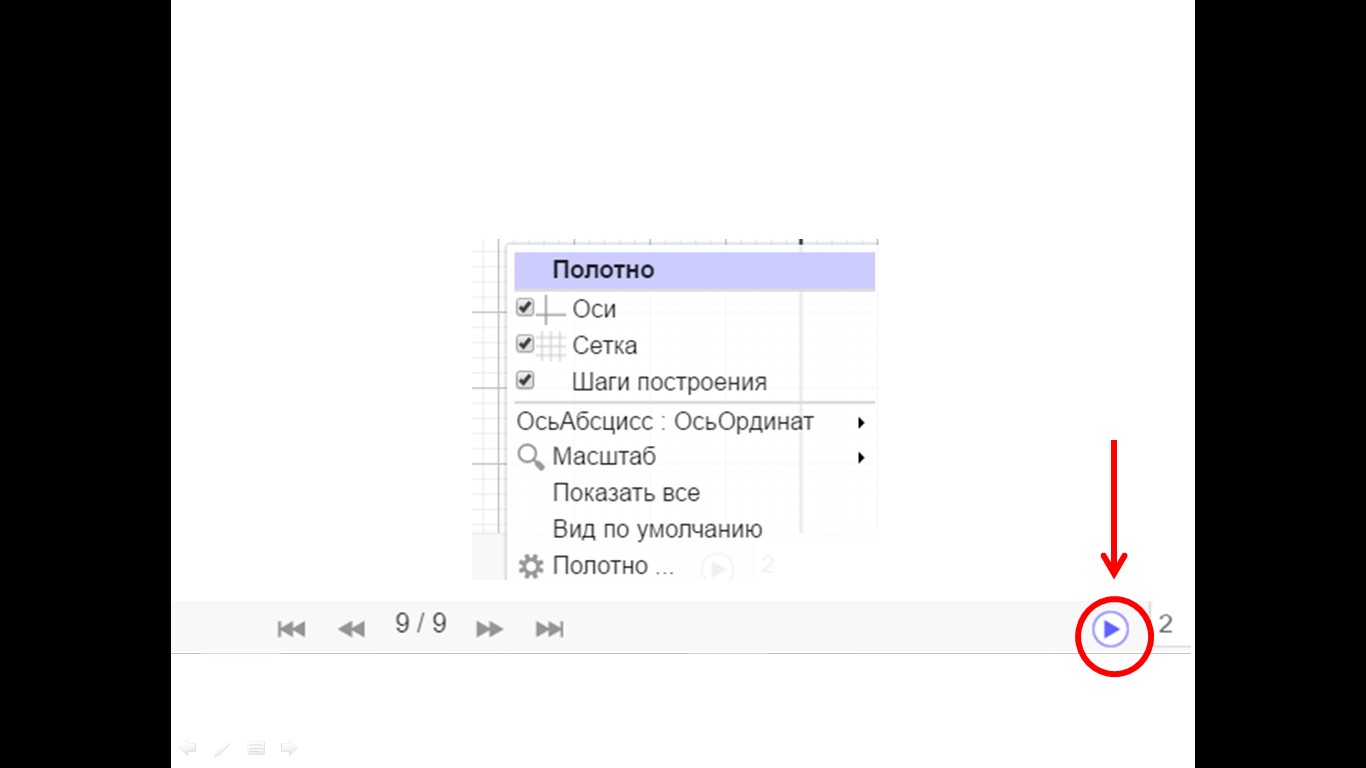Рисунок 17 Просмотр построенияПостроим пирамиду. Для этого, необходимо выбрать Главное меню – Вид – Полотно 3D. Выбираем функцию Пирамида и отмечаем 4 точек на координатной оси (рис. 18). 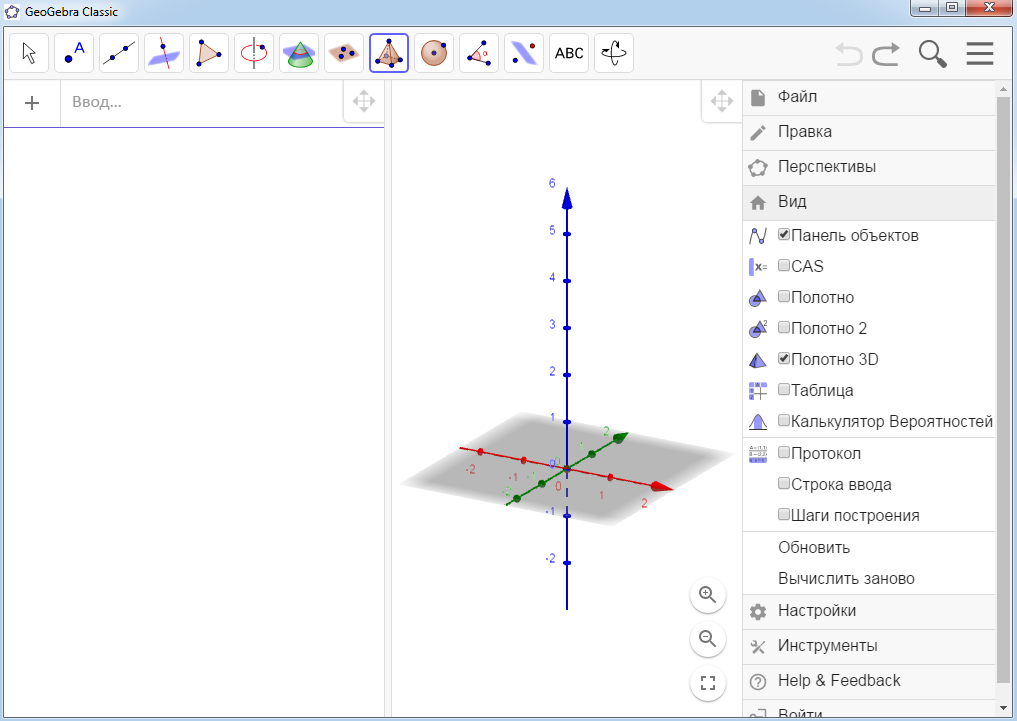Рисунок 18 Координатная ось Нажимая по оси z на нужную нам высоту и после переименования точки на оси z получим пирамиду ABCDE (рис. 19). 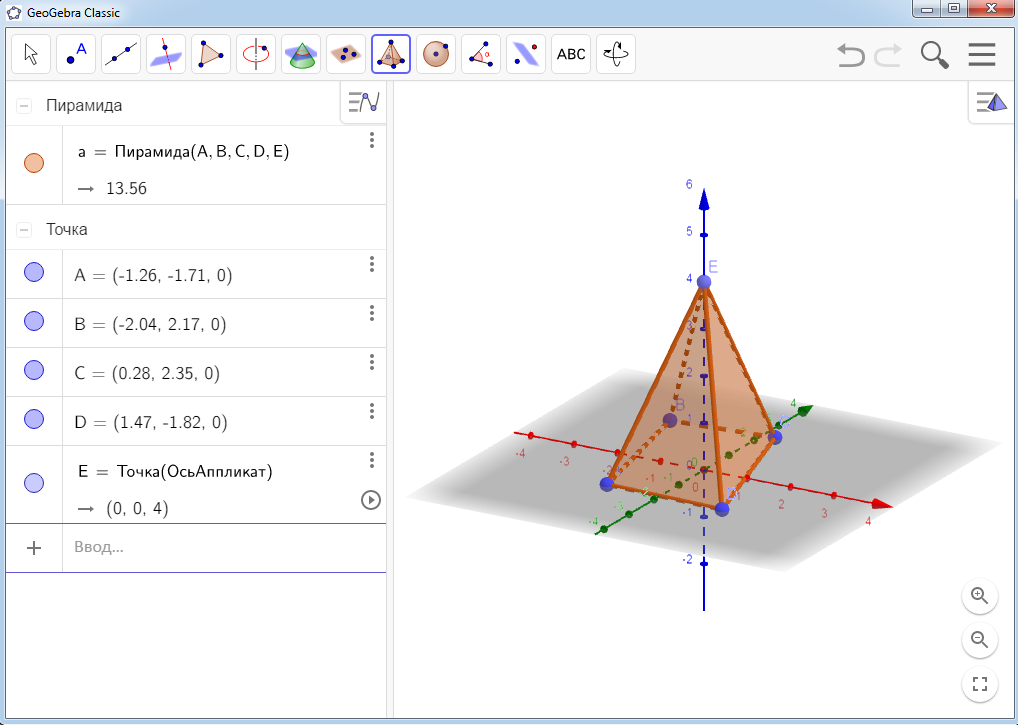Рисунок 19 ПирамидаABCDE

Интерактивную геометрическую среду GeoGebra можно считать достойной программой для ее внедрения в образовательный процесс. Данная программа имеет огромный спектр возможностей и, непременно, заинтересует учащихся, так как в ней даже можно выполнять некоторые школьные задания по таким предметам как «Алгебра» и «Геометрия». Так же достоинством этой ИГС является то, что она бесплатная. Она имеет встроенный командный язык. В данной работе использованы лишь простейшие инструменты и команды, приведены примеры решения практических заданий.

Список использованных источников

1. Иванчук, И. В. Использование компьютерной программы GeoGebra на уроках математики в 7-11 классах: методическое пособие / И. В. Иванчук, О. В. Эйкен, Е. В. Мартынова, Ю. В. Самылова. – Мурманск : МГПУ, 2008. – 38 с. – Текст : непосредственный. 2. Hohenwarter, J. Введение в GeoGebra / J. Hohenwarter, M. Hohenwarter. – Австрия, 2012. – 153 с. – Текст : непосредственный. 3. Чеботарева, Э. B. Компьютерный эксперимент с GeoGebra / Э. В. Чеботарева. – Казань: Казанский ун-т, 2015 – 61 с. – Текст : непосредственный.

Источник: kopilkaurokov.ru

Полезные материалы

Достаточно важным навыком, необходимым для правильного решения тригонометрических задач, является навык изображения чисел точками на единичной окружности.

Для отработки этого навыка попробуем создать интерактивный чертеж, который позволит отработать решение задач типа 4.5 — 4.11 (см. Алгебра 10-11. Задачник. Под редакцией Мордковича А.Г.). Идея создания этого материала принадлежит Гоглевой С.К. (goglevask) Чертеж будем создавать в программе GeoGebra. В настоящее время актуальной является версия GeoGebra 5, которую можно скачать на официальном сайте программы

Руководство по работе с программой для начинающих находится здесь

Сразу отмечу, что все написанное ниже не претендует на звание абсолютной истины.

1. Запускаем программу (если она не установлена, то нужно установить. Или воспользоваться online версией, расположенной на официальном сайте)
2. Выбираем Перспективу » Алгебра и графики » (см.рис.1)
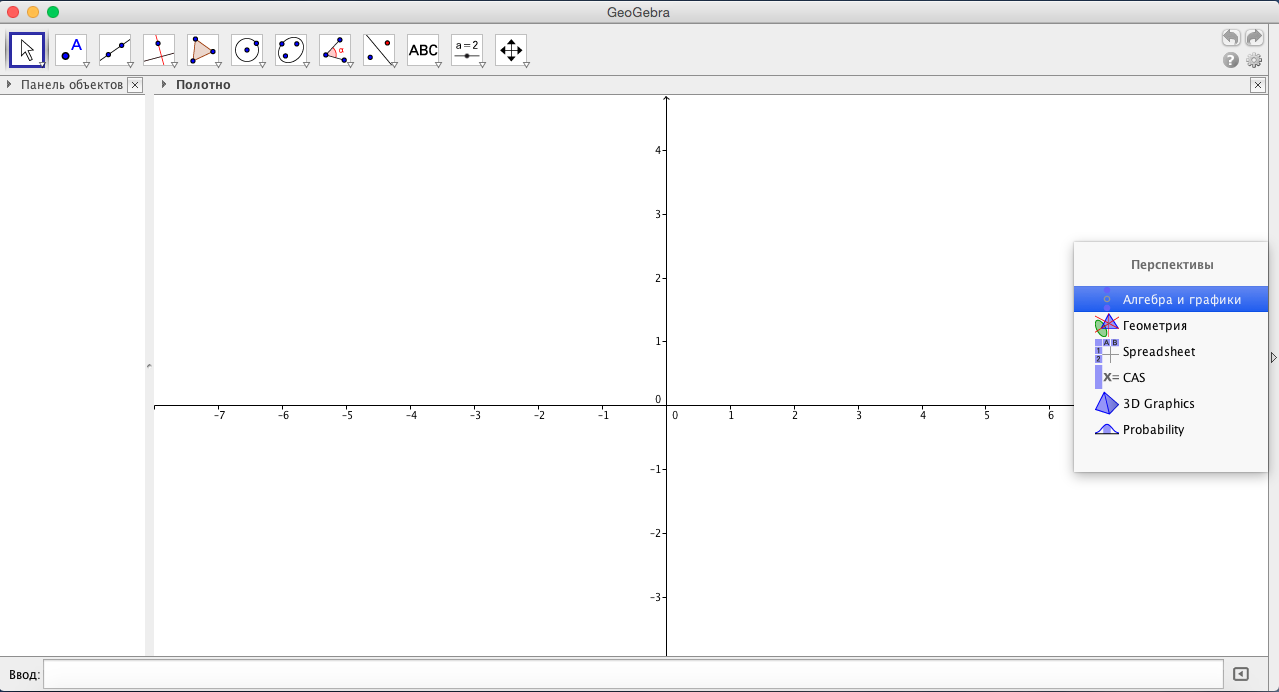
3. Начинаем создавать оформление для своего интерактивного чертежа. Желательно, чтобы все чертежи созданные для определенной группы учащихся, или для определенной группы уроков, были в одном стиле. Поэтому создадим шаблон. Делается следующим образом: » Настройки-дополнительно » открывается панель настроек. Выберем вкладку » Настройки-Полотно » (см.рис.2)
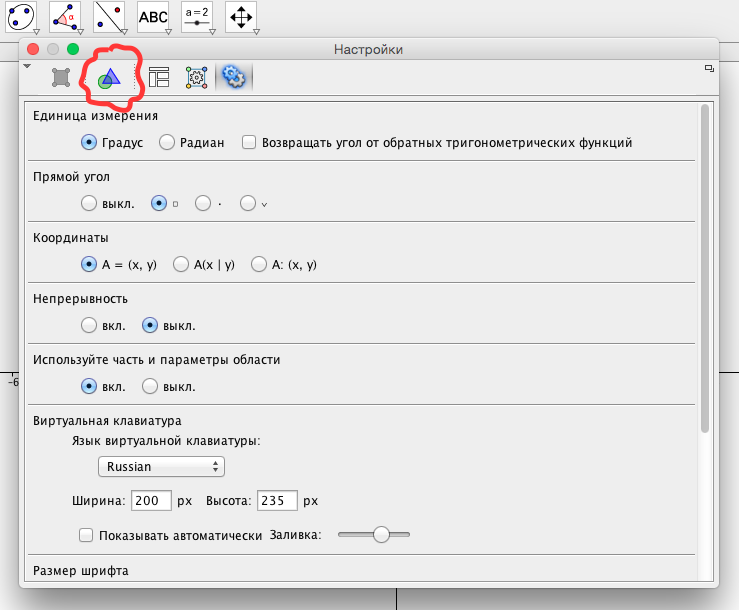
4. Затем можно задать цвет полотна, отключить отображение осей координат (в данном случае они не нужны) и подключить изображение сетки (см.рис.3).
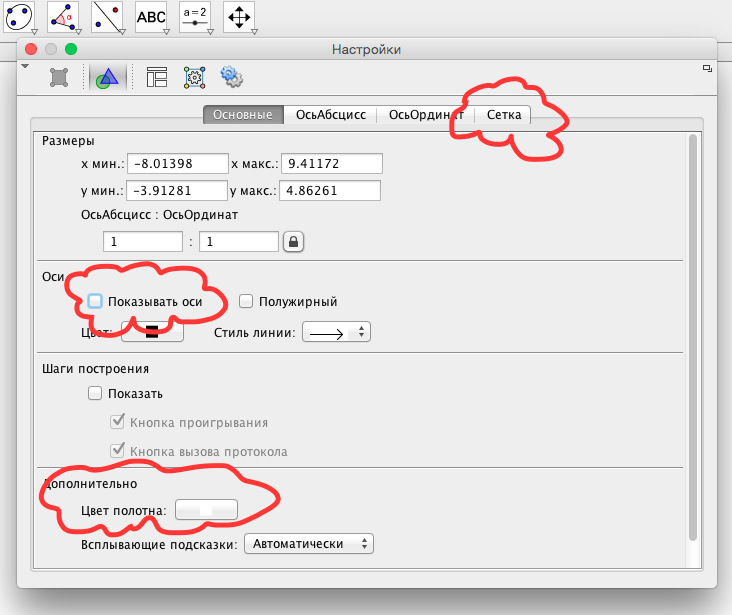
5. Заготовка для интерактивного чертежа готова. Можно начинать работу (Полученный файл желательно сохранить).
6. Построим единичную окружность. Для этого выберем инструмент » Окружность по центру и радиусу » (см.рис.4) и, поставив точку в один из узлов сетки, введем в открывшееся поле значение радиуса. (Радиус нужно выбирать так, чтобы окружность получилась не слишком маленькой)
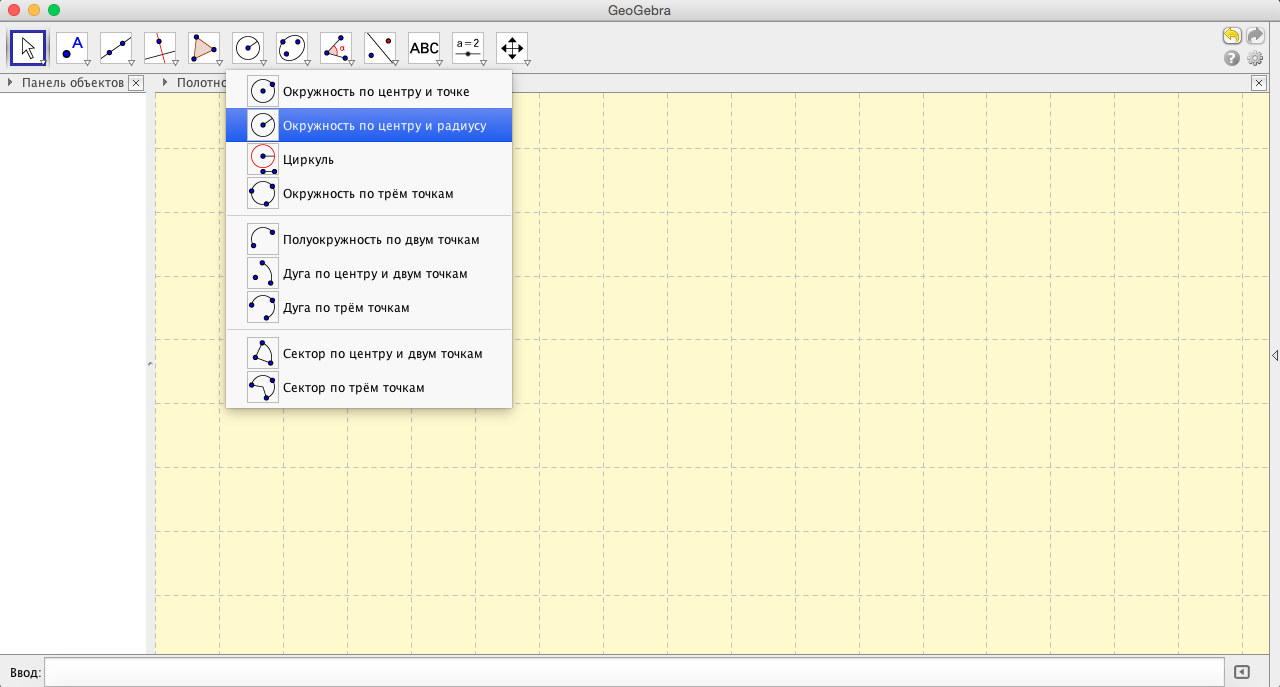
7. Переименуем центр окружности (см.рис.5) и скроем обозначение. Это делается для того, чтобы можно было добавить обозначение в виде надписи с более крупным шрифтом, чтобы люди с ослабленным зрением могли не напрягаясь видеть обозначения на чертеже.
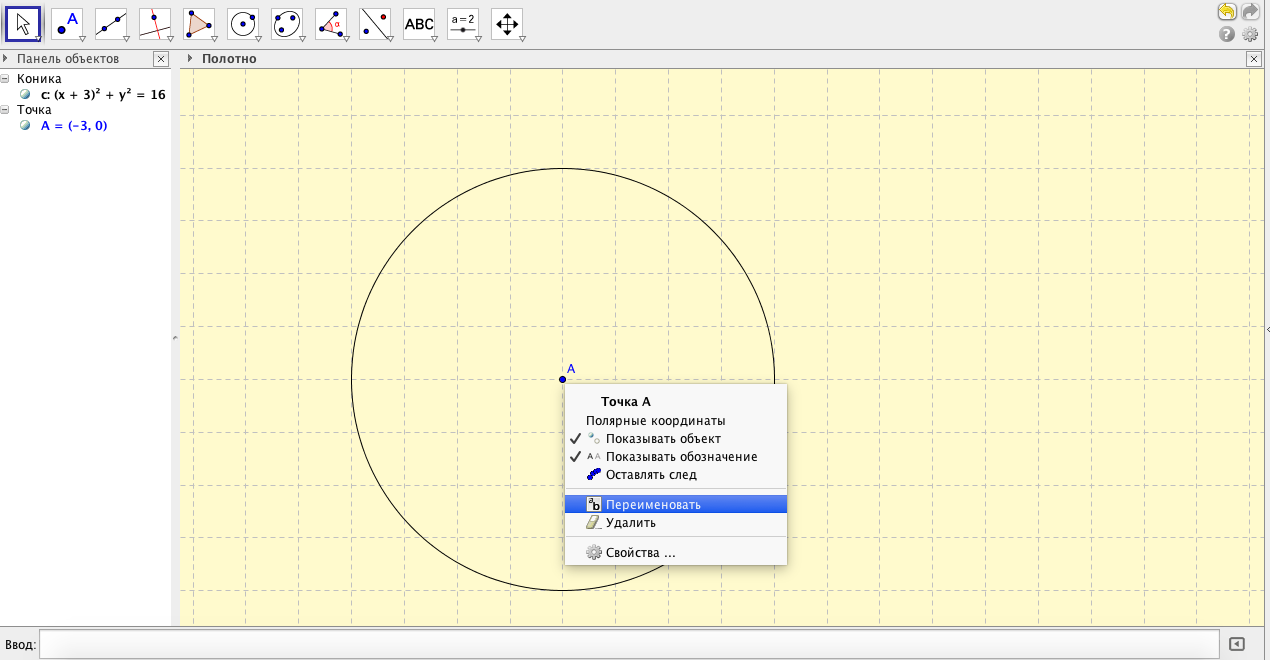
8. Щелчком правой кнопки мыши на окружности вызовем контекстное меню и настроим свойства окружности (см.рис.6). Здесь можно выбрать цвет, толщину, стиль линии.
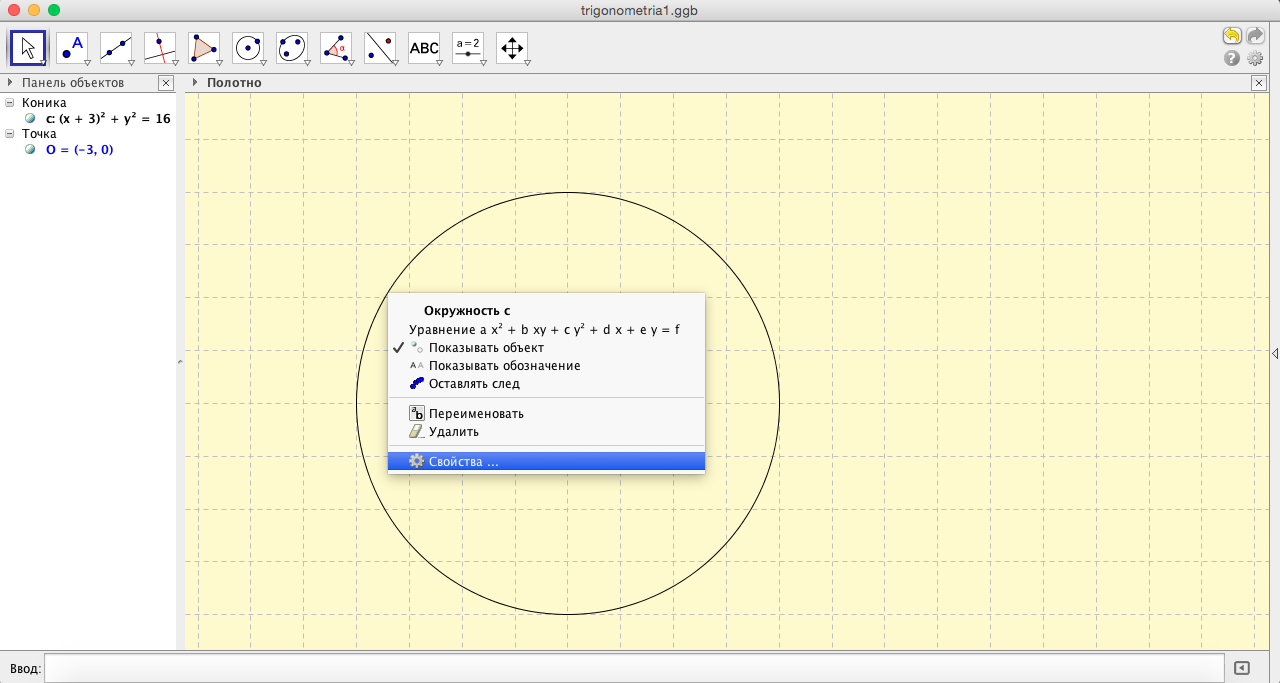
9. Чтобы пользователи не могли случайно сдвинуть окружность, ее нужно закрепить (см.рис.7). Вообще следует взять за правило закреплять все объекты, которые не должны перемещаться по чертежу.
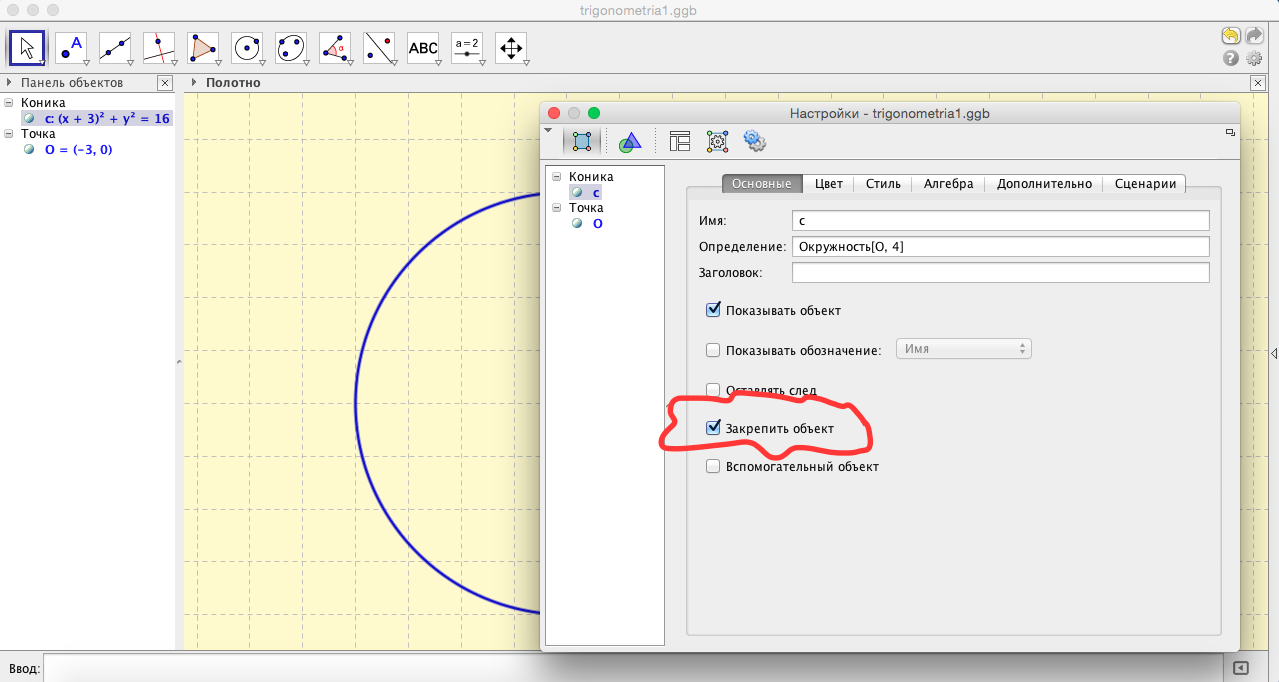
10. С помощью инструмента «Вектор» изобразим систему координат (см.рис.8). Почему нельзя воспользоваться встроенным изображением осей координат? Потому, что во встроенном изображении оси координат проходят через все поле чертежа. Нам же желательно ограничить размер осей.
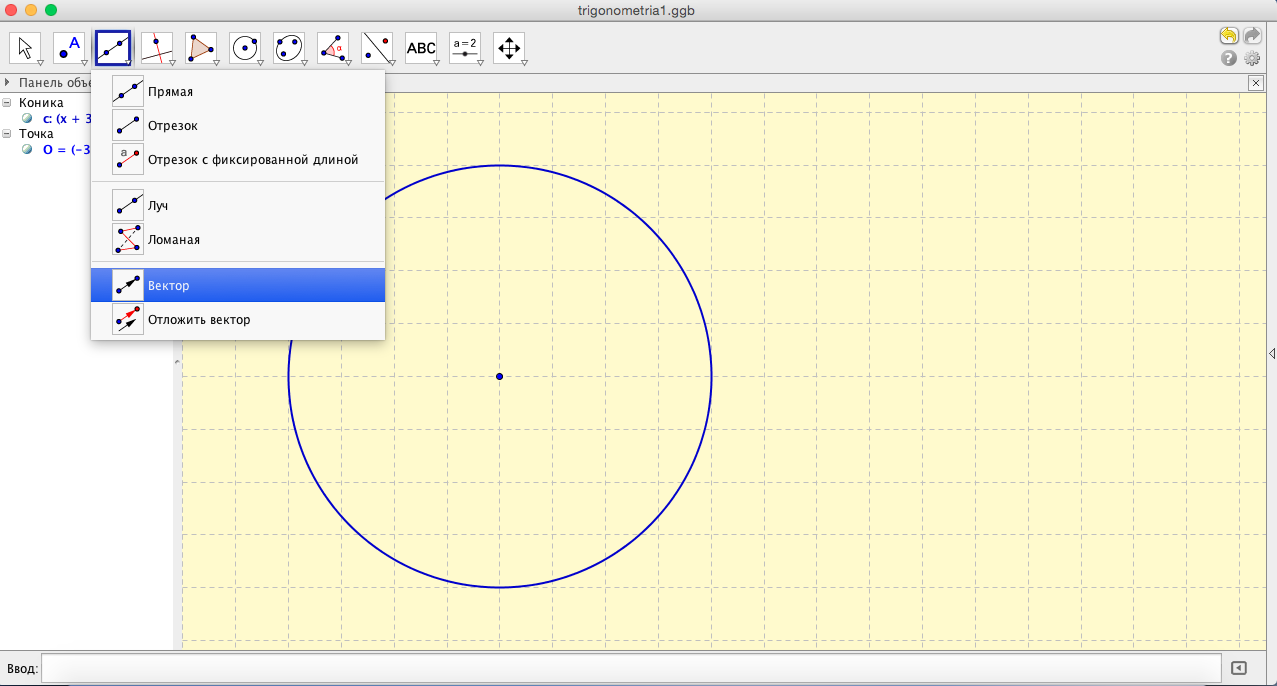
11. Нарисовав оси, настроим свойства векторов: цвет, стиль линии, . Не забываем закреплять готовые объекты. Скроем начальные и конечные точки векторов. После чего можно заняться подписями. (см.рис.9). Выберем инструмент «Текст», введем обозначение начала координат «O»
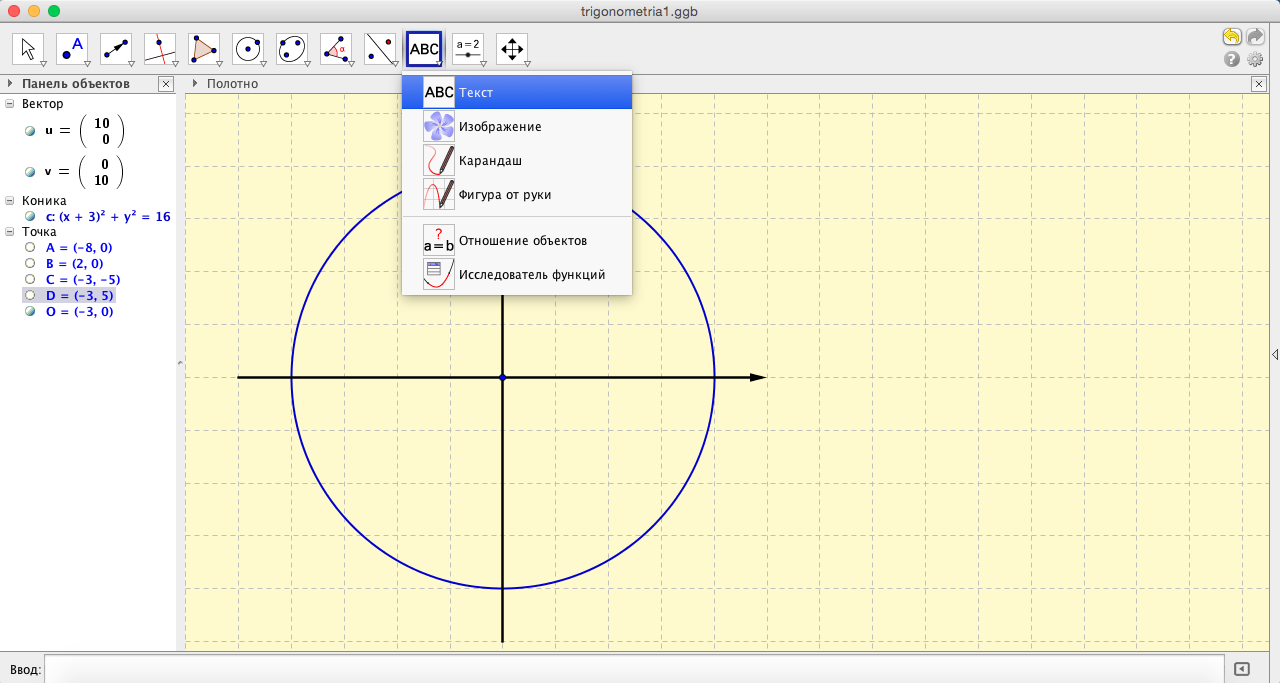
12. После чего в свойствах надписи настроим шрифт, размер шрифта, цвет шрифта. Чтобы надпись привязать к началу координат зададим начальную точку (см.рис.10). Надпись свяжем с точкой O и сдвинем ее от точки O на некоторый вектор. (В данном случае вектор подобран экспериментально).
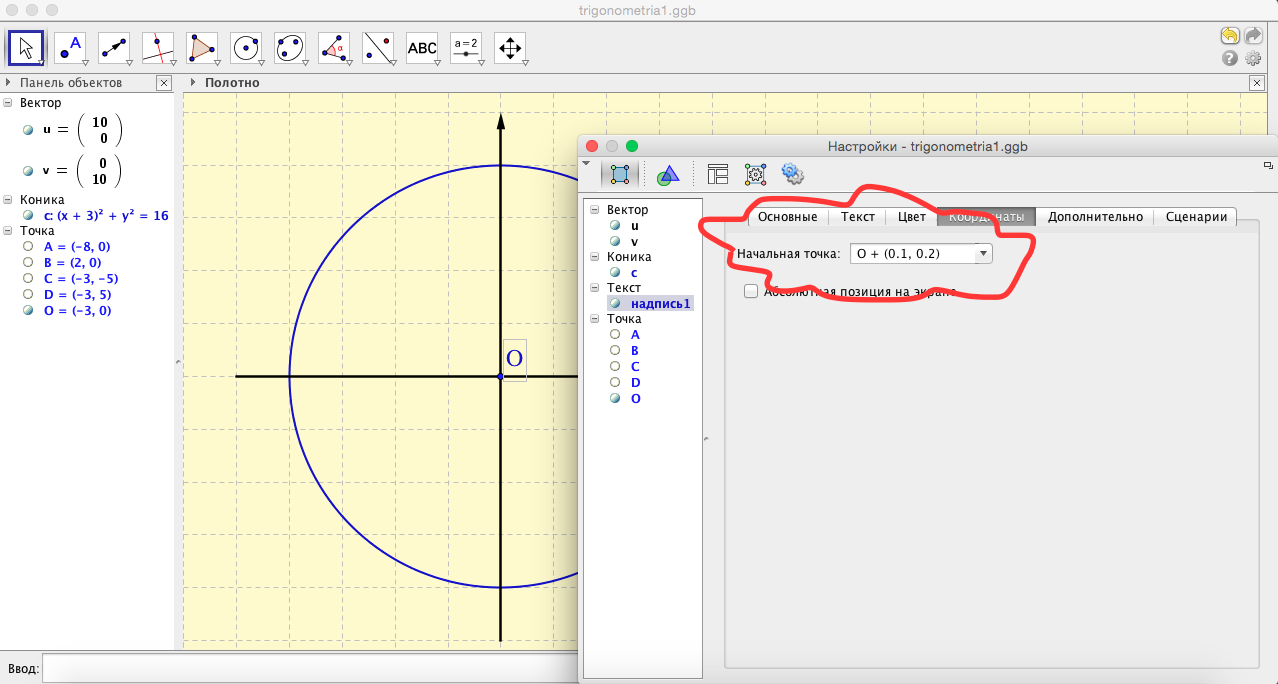
13. Аналогично создадим подписи для осей координат (см.рис.11). Не забываем закреплять готовые объекты.
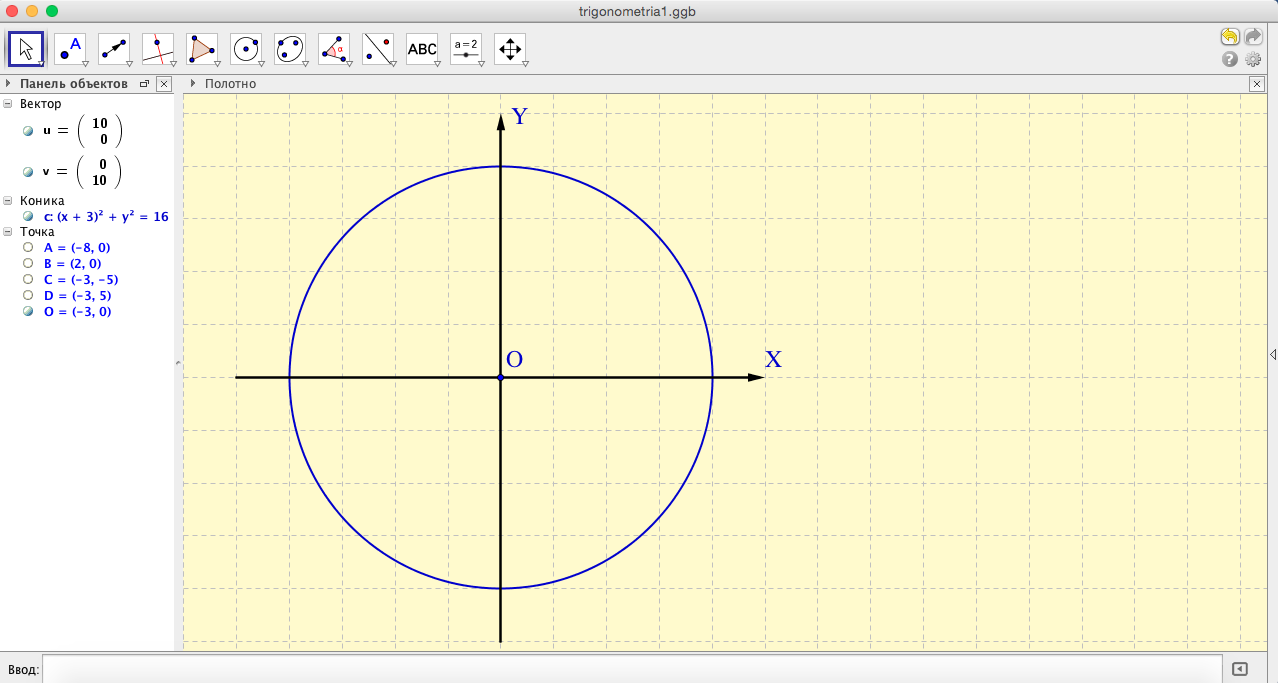
14. Теперь расставим на окружности точки, соответствующие «хорошим» углам. Проще всего ставятся точки на пересечении окружности с осями координат (см.рис.12).
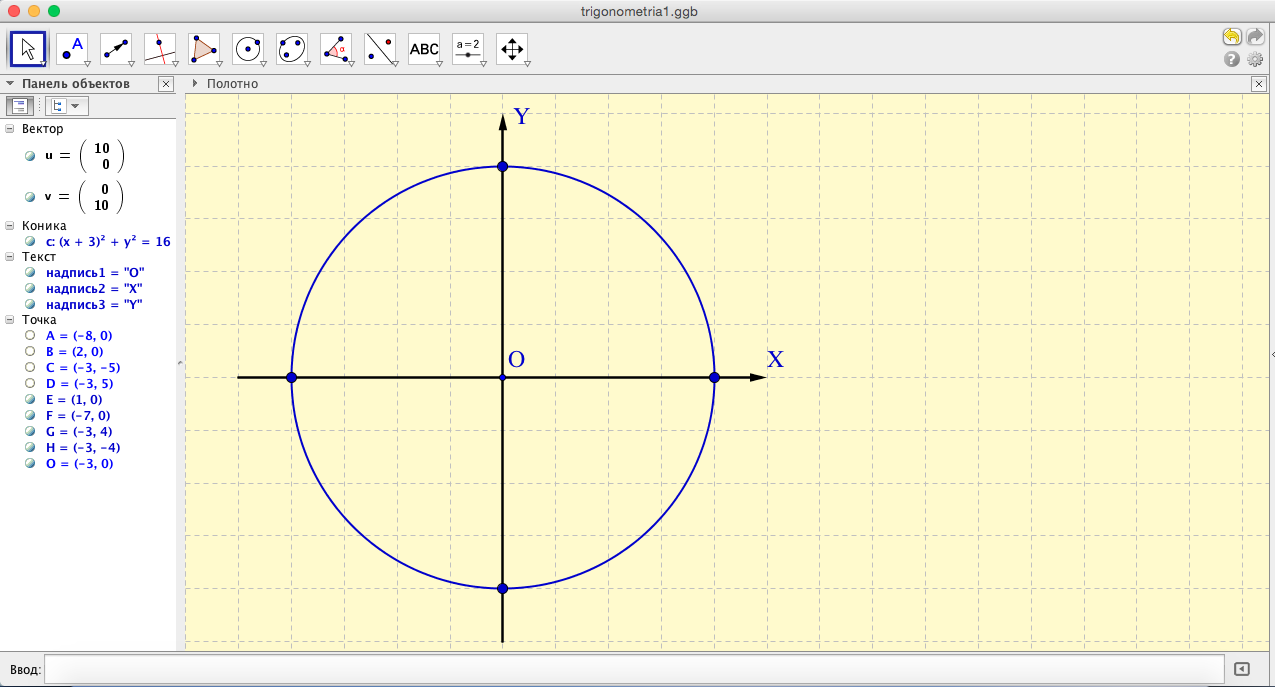
15. Для изображения остальных точек воспользуемся инструментом «Угол заданной величины» (см.рис.13). Щелкаем левой кнопкой мыши на точке пересечения оси OX с единичной окружностью, затем на точке O (это вершина угла), после чего вводим в открывшейся форме величину и направление угла. Затем изображение угла скрываем.
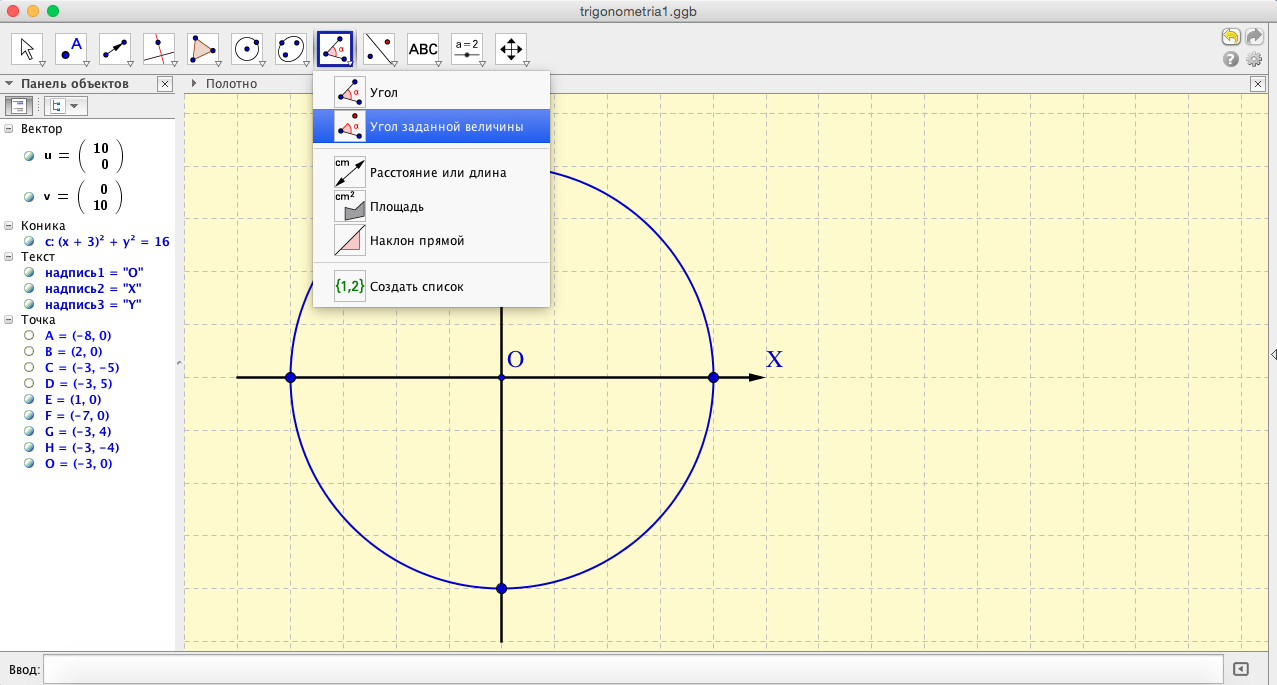
16. Так выглядит окружность со всеми расставленными точками.
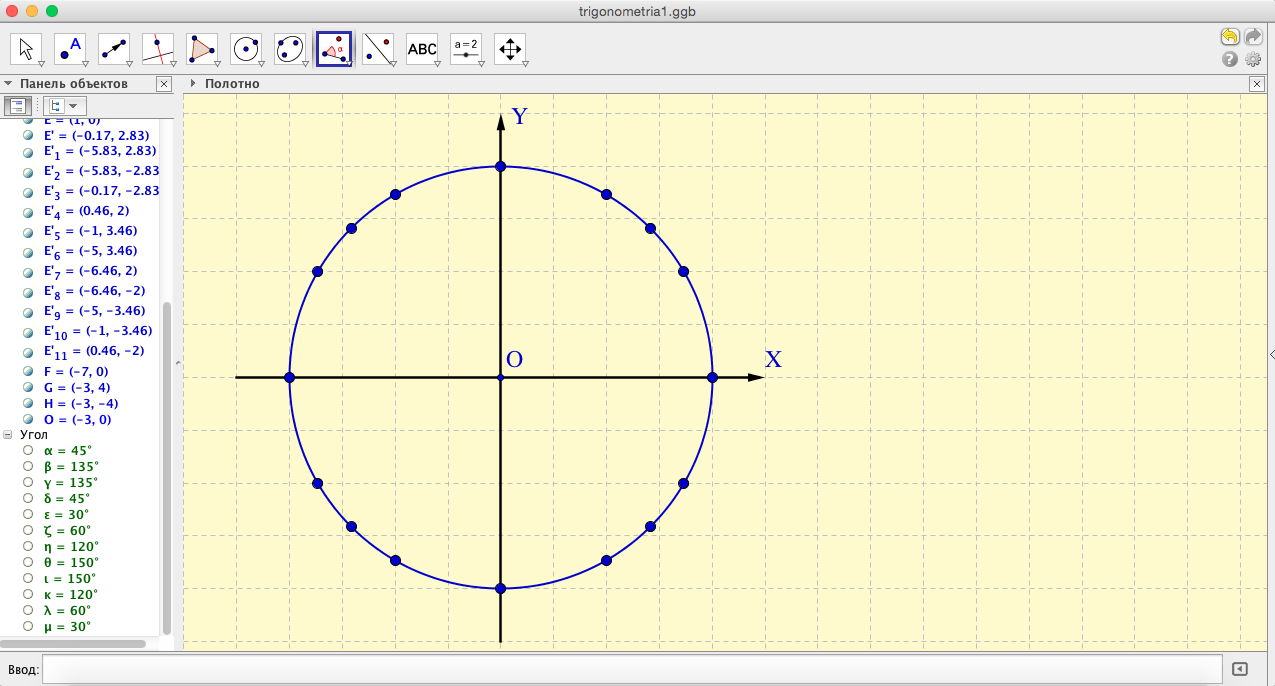
17. Теперь сформулируем условие задачи. Используем инструмент «Текст». Подберем шрифт, размер, цвет шрифта и расположение условия задачи на поле.
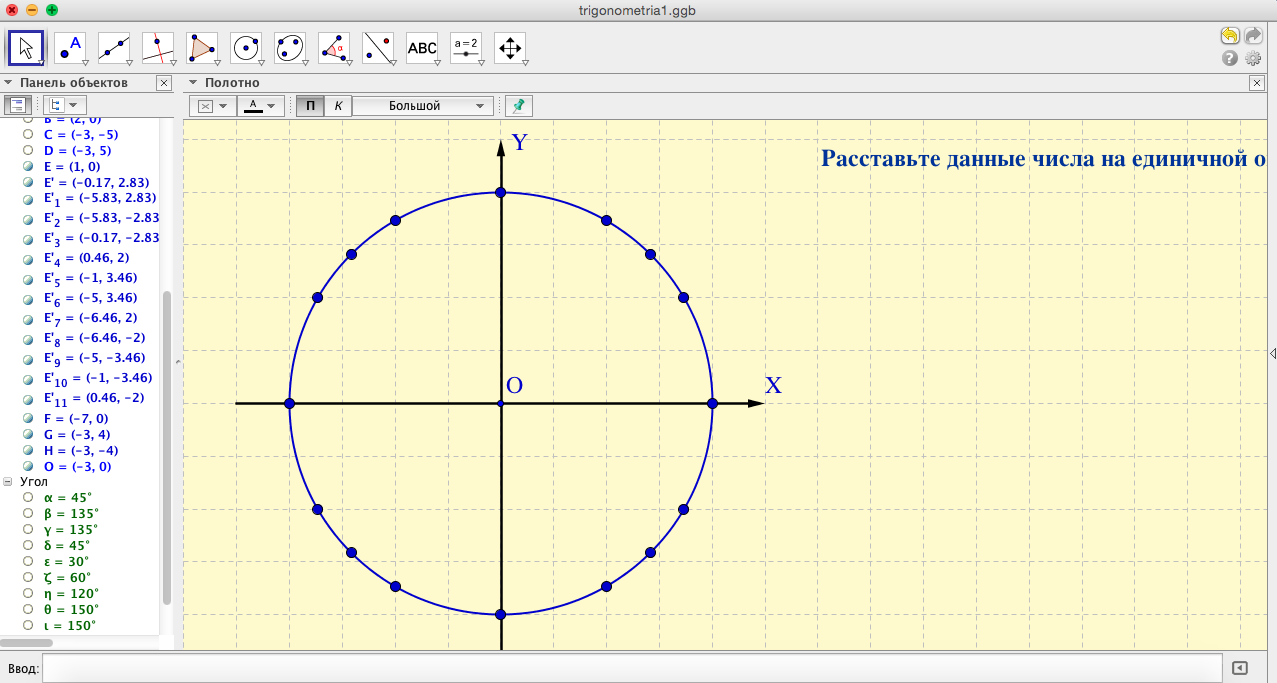
18. Теперь добавим на чертеж интерактивные элементы. Т.е. такие элементы, которые пользователь может перемещать по полю чертежа. С помощью инструмента «Текст» создадим надписи с числами. Эти надписи не нужно закреплять, чтобы осталась возможность их перемещения.
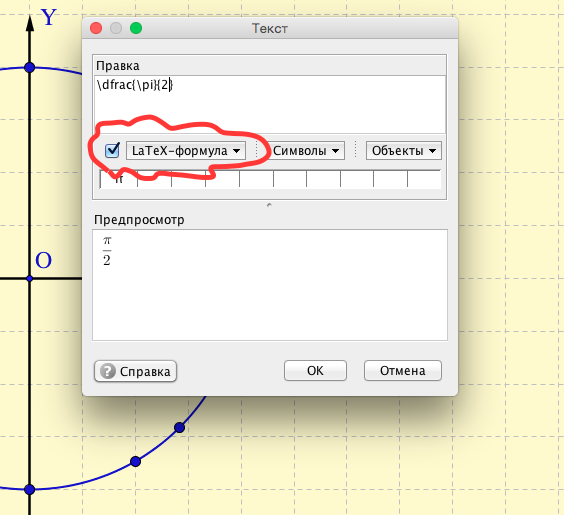
19. После создания надписей для всех чисел (для каждого числа своя надпись) можно скрыть «Панель объектов» (см.рис)
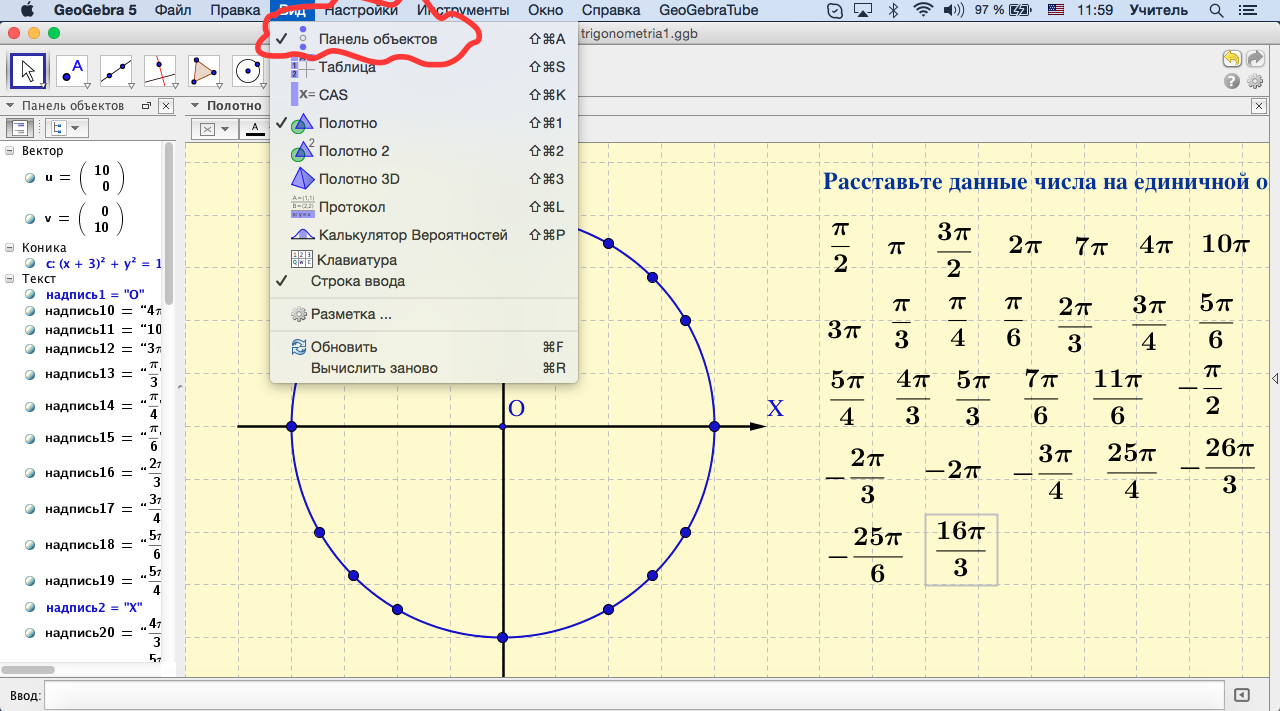
20. Вот так выглядит почти готовый проект. Осталось сохранить его.

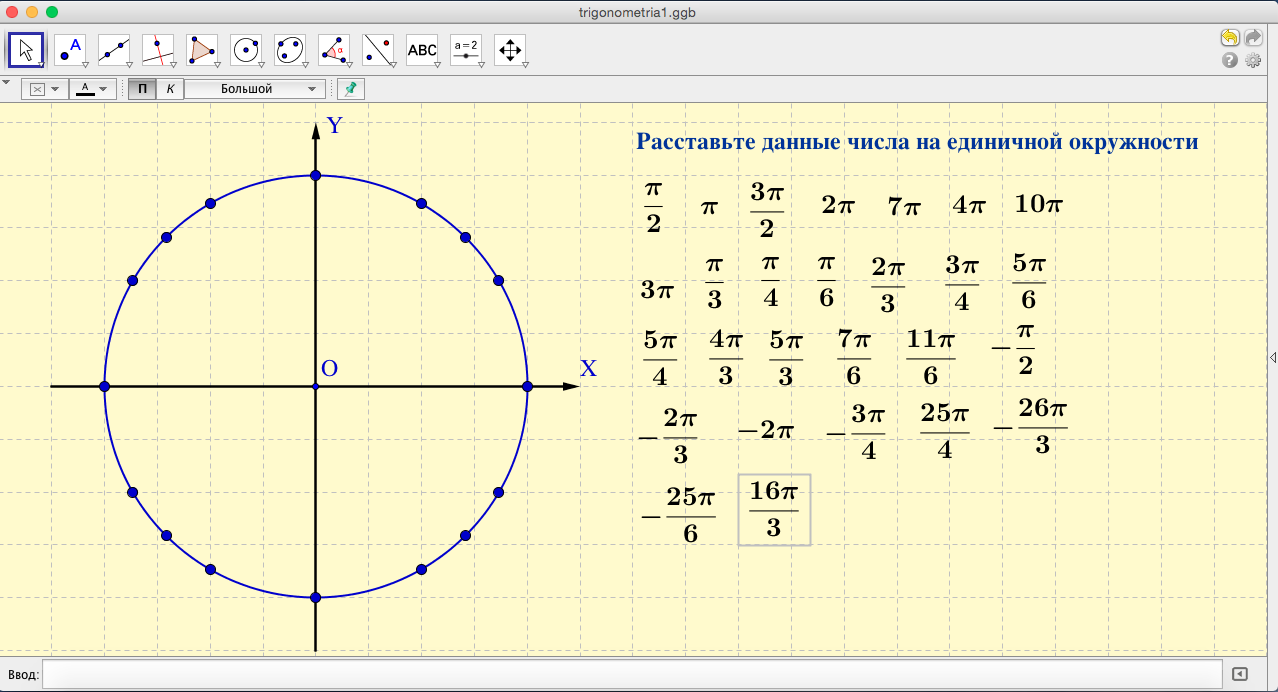
Пользователь должен расставить надписи около соответствующих точек на единичной окружности.

На этом заканчивается Шаг №1 на пути создания интерактивного чертежа.

Источник: zdod-matem.ucoz.com