В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №10 ЕГЭ.
Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)
Какой путь вы выберете + десятки дерзких задачек
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 10 в формате ЕГЭ-2021
Линейная функция
1. На рисунке изображён график функции . Найдите значение , при котором

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:
Вычтем из первого уравнения второе:
Уравнение прямой имеет вид:
Найдем, при каком значение функции равно -13,5.
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Запишем формулы функций.
Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция
Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции
Вычтем из первого уравнения второе.
Прямая задается формулой:
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).
Для прямой, расположенной выше, угловой коэффициент равен
Эта прямая проходит через точку (-2; 4), поэтому: эта прямая задается формулой
Теория вероятностей | Математика TutorOnline
Для точки пересечения прямых:
Квадратичная функция. Необходимая теория
4. На рисунке изображен график функции Найдите b.

На рисунке — квадратичная парабола полученная из графика функции сдвигом на 1 вправо, то есть
5. На рисунке изображен график функции . Найдите с.

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид .
6. На рисунке изображён график функции Найдите

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:
Формула функции имеет вид:
7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому
График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:
Найдем абсциссу точки B. Для точек A и B:
(это абсцисса точки A) или (это абсцисса точки B).
Степенные функции. Необходимая теория
8. На рисунке изображены графики функций и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

График функции проходит через точку (2; 1); значит,
График функции проходит через точки (2; 1) и (1; -4), — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда
Для точек A и B имеем:
Отсюда (абсцисса точки A) или (абсцисса точки B).
9. На рисунке изображён график функции . Найдите f (6,76).

Функция задана формулой:
Ее график проходит через точку (4; 5); значит,
10. На рисунке изображен график функции . Найдите .

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.
Показательная функция. Необходимая теория
11. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:
Поделим второе уравнение на первое:
Подставим во второе уравнение:
12. На рисунке изображен график функции . Найдите

График функции проходит через точку Это значит, что
формула функции имеет вид: .
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.
Вычтем из второго уравнения первое:
или — не подходит, так как (как основание логарифма).
14. На рисунке изображен график функции .

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:
Тригонометрические функции. Необходимая теория
15. На рисунке изображён график функции Найдите

График функции сдвинут на 1,5 вверх; Значит, Амплитуда (наибольшее отклонение от среднего значения).
Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на .
16. На рисунке изображён график функции
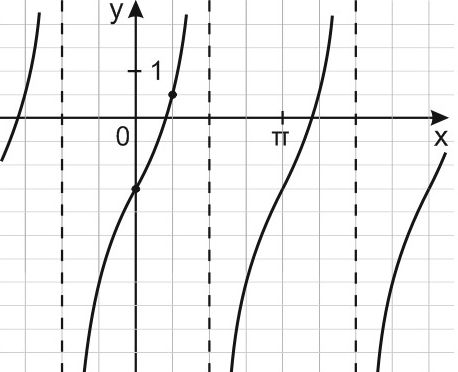
На рисунке — график функции Так как
График функции проходит через точку A Подставим и координаты точки А в формулу функции.
Так как получим:
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то
Пользуясь периодичностью функции , период которой T = 4, получим:
Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 07.06.2023
Источник: ege-study.ru
Задание 1
Вопрос:
Установите соответствие между оператором и значением d после его выполнения.
Укажите соответствие для всех 5 вариантов ответа:
1) 0.5__ d:=round (5.5)
2) 5__ d:=int (5.5)
3) 6__ d:=frac (5.5)
4) 30.25__ d:=sqrt (5.5)
5) 2.34520787991171__ d:=sqr (5.5)
Задание 2
Вопрос:
Какие из указанных операций и функций являются общими для всех числовых типов?
Выберите несколько из 4 вариантов ответа:
1) Вычитание 2) Сложение 3) Округление 4) Выделение целой части
Задание 3
Вопрос:
Какие из указанных, неявных преобразований возможны в программах на языке Паскаль?
Выберите несколько из 4 вариантов ответа:
1) Из byte в real 2) Из byte в integer 3) Из real в integer 4) Из integer в byte
Задание 4
Вопрос:
Из указанных операций и функций выберите определённые только для целочисленных типов?
Выберите несколько из 4 вариантов ответа:
1) frac 2) int 3) random (a) 4) div
Задание 5
Вопрос:
Какое значение будет иметь a после выполнения оператора a:=int (20.75)?
Выберите один из 4 вариантов ответа:
1) 21 2) 21.75 3) 20 4) 0.75
Задание 6
Вопрос:
При помощи какой функции можно преобразовать значение вещественного типа в целочисленное?
Выберите один из 4 вариантов ответа:
1) sqr 2) round 3) frac 4) int
Задание 7
Вопрос:
Как сгенерировать случайное целое число на промежутке от 3 до 100, включая концы?
Выберите один из 4 вариантов ответа:
1) 3+random (98) 2) random (100)-3 3) 3+random (97) 4) random (103)-6
Задание 8
Вопрос:
Каков будет результат выполнения программы представленной на рисунке?
Изображение: Выберите один из 4 вариантов ответа:
1) Ошибка преобразования типов
2) Вывод: 56250
3) Вывод: 5625
4) Вывод: 90
Задание 9
Вопрос:
Какое значение будет иметь t после выполнения оператора t:=274 mod 4?
Выберите один из 4 вариантов ответа:
1) 2 2) 4 3) 68 4) 0
Задание 10
Вопрос:
Как называется алгоритм, в котором присутствует только алгоритмическая конструкция «следование»?
Выберите один из 4 вариантов ответа:
1) Линейный 2) Циклический 3) Разветвляющийся 4) Вспомогательный
На этот вопрос еще никто не ответил. Напишите свой ответ или воспользуйтесь поиском:
Источник: znanijam.net
Дана программа. Что получится в результате выполнения программы. program perimetr_1; var a,b,p:real; begin a: = 2; b: = 14; p:=2*(a+b); writeln(‘p=’,p:5:0) end.
Дана программа. Что получится в результате выполнения программы.
program perimetr_1;
var
a,b,p:real;
begin
a: = 2;
b: = 14;
p:=2*(a+b);
writeln(‘p=’,p:5:0)
end.