1. Какое количество информации несет в себе сообщение о том, что нужная вам программа находится на одной из восьми дискет?
Дано: N=8 — количество дискет (число событий)
2. Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8х8 после первого хода первого игрока, играющего крестиками?
N=64 — количество полей
3. Сообщение о том, что ваш друг живет на десятом этаже несет в себе 4 бита информации. Сколько этажей в доме?
4. В коробке 5 синих и 15 красных шариков. Какое количество информации несет сообщение, что из коробки достали синий шарик?
N=15+5=20 всего шариков
K=5 — синих (его достали)
5. Какое количество информации о цвете вынутого шарика будет получено, если в непрозрачном пакете хранятся: 10 белых, 20 красных, 30 синих и 40 зеленых шариков?
K=10+20+30+40=100 — общее количество шариков
N1=10; N2=20; N3=30; N4=40;
Pзел. = 40/100 = 0,4
6. Студенты группы изучают один из трех языков: английский, немецкий или французский. Причем 12 студентов не учат английский. Сообщение, что случайно выбранный студент Петров изучает английский, несет log23 бит информации, а что Иванов изучает французский — 1 бит. Сколько студентов изучают немецкий язык?
Урок № 4. Алфавитный и содержательный подходы к информации
Y — учат французский
X — учат английский, 12 не учат английский. Всего 12+X студентов
18-X-Y=18-6-9=3 студента изучают немецкий.
Алфавитный подход к измерению информации
Если информация представлена в виде дискретного сообщения, то логично считать количеством информации его длину, то есть общее число знаков в сообщении. Но длина сообщения зависит не только от содержащейся в нем информации. На нее влияет мощность алфавита используемого языка. Чем меньше знаков в используемом алфавите, тем длиннее сообщение. Так, например, в алфавите азбуки Морзе всего три знака (точка, тире, пауза), поэтому для кодирования каждой русской или латинской буквы нужно использовать несколько знаков, и текст, закодированный по Морзе, будет намного длиннее, чем при обычной записи.
Пример: Сигнал SOS: 3 знака в латинском алфавите;
11 знаков в алфавите Морзе: *** пауза — — — пауза ***.
Для упорядочивания измерений информационный объем сообщений принято измерять в битах. Один бит соответствует одному знаку двоичного алфавита. Итак, чтобы измерить длину сообщения, его нужно представить в двоичном виде и подсчитать количество двоичных знаков — битов. При этом совсем не обязательно уметь интерпретировать сообщения.
Пример. Пусть сообщение в двоичном алфавите выглядит следующим образом: 000100010001. Мы не знаем, какая информация была заложена в этом сообщении, но можем легко подсчитать его длину — 12 двоичных знаков, следовательно, его информационный объем равен 12-ти битам.
Если алфавит содержит 2 i знаков, то каждый из его знаков можно закодировать с помощью i знаков двоичного алфавита. Таким образом, объем информации I, содержащейся в сообщении длиной k при использовании алфавита мощностью 2 i , равен
Как измерить количество информации?
Пример. Найдем информационный объем слова SOS, записанного в компьютерной кодировке. При кодировании букв в компьютере используется либо алфавит ASCII (American Standard Code for Information Interchange — американский стандартный код обмена информацией), состоящий из 2 8 =256 знаков, либо алфавит Unicode, мощность которого 2 16 = 65536. В слове SOS три буквы, следовательно, его информационный объем 3*8=24 или 3*16=48 бит, в зависимости от используемой кодировки.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита. При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации. Сама единица измерения информации «бит» получила свое название от английского сочетания «binary digit» — «двоичная цифра».
Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле: i=log2N, где — N мощность алфавита.
Применение алфавитного подхода удобно прежде всего при использовании технических средств работы с информацией. В этом случае теряют смысл понятия «новые — старые», «понятные — непонятные» сведения. Алфавитный подход является объективным способом измерения информации в отличие от субъективного содержательного подхода.
Ограничения на максимальный размер алфавита теоретически не существует. Однако есть алфавит, который можно назвать достаточным. Это алфавит мощностью 256 символов. В алфавит такого размера можно поместить все практически необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания.
Поскольку 256 = 2 8 , то один символ этого алфавита «весит» 8 бит.
Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов. В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов; полученное число даст информационный объем текста в байтах.
Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов. Значит, страница содержит 40×60=2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт.
информационный алфавитный компьютерный кодировка
Источник: studbooks.net
Какое количество информации несет сообщение о том что нужная вам программа
Вопрос по информатике:
Какое количество информации несет в себе сообщение о том, что нужная вам программа находится на одной из 16 дискет?
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- bookmark_border
- 03.06.2018 18:25
- Информатика
- remove_red_eye 1392
- thumb_up 36
Ответы и объяснения 1
N=, N-кол-во равновероятных событий (16), i- кол-во бит на одно событие.
16=, i=4 бита
Ответ 4 бита
- 04.06.2018 17:56
- thumb_up 49
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Информатика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.
Источник: online-otvet.ru
Содержательный подход к измерению информации
Другое название содержательного подхода – вероятностный. Вероятность — степень возможности появления какого-либо определенного события в тех или иных условиях. Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N.
Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней. Результаты данного опыта могут быть следующие: выпадение грани с одним из следующих знаков: 1, 2, . . . N.
Введем в рассмотрение численную величину, измеряющую неопределенность — энтропию (обозначим ее H). Согласно развитой теории, в случае равновероятного выпадания каждой из граней величины N и H связаны между собой формулой Хартли H = log2N.
Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, H будет равно единице при N = 2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты при котором возможны два исхода: «орел», «решка»). Такая единица количества информации и является «битом».
Приведем примеры равновероятных сообщений: при бросании монеты: «выпала решка», «выпал орел»; на странице книги: «количество букв чётное», «количество букв нечётное».
Определим теперь, являются ли равновероятными сообщения «первой выйдет из дверей здания женщина» и «первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Вероятность события А определяется формулой:
где m — число элементарных исходов, благоприятствующих А;
n — число всех возможных элементарных исходов испытания.
Легко заметить, что если вероятности p1, . pNравны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли.
Рассмотрим следующий пример. Пусть при бросании несимметричной четырехгранной пирамидки вероятности выпадения граней будут следующими: p1=1/2, p2=1/4, p3=1/8, p4=1/8, тогда количество информации, получаемое после броска, можно рассчитать по формуле:
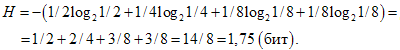
Для симметричной четырехгранной пирамидки количество информации будет: H=log24=2(бит).
Заметим, что для симметричной пирамидки количество информации оказалось больше, чем для несимметричной пирамидки. Максимальное значение количества информации достигается для равновероятных событий.
1. Какое количество информации несет в себе сообщение о том, что нужная вам программа находится на одной из восьми дискет?
N=8 – количество дискет (число событий)
Ответ:3 бита
2. Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8х8 после первого хода первого игрока, играющего крестиками?
N=64 – количество полей
Ответ:6 бит
3. Сообщение о том, что ваш друг живет на десятом этаже несет в себе 4 бита информации. Сколько этажей в доме?
4. В коробке 5 синих и 15 красных шариков. Какое количество информации несет сообщение, что из коробки достали синий шарик?
N=15+5=20 всего шариков
K=5 – синих (его достали)
Ответ:2 бита.
5. Какое количество информации о цвете вынутого шарика будет получено, если в непрозрачном пакете хранятся: 10 белых, 20 красных, 30 синих и 40 зеленых шариков?
K=10+20+30+40=100 – общее количество шариков
Ответ:1,85 бита
6. Студенты группы изучают один из трех языков: английский, немецкий или французский. Причем 12 студентов не учат английский. Сообщение, что случайно выбранный студент Петров изучает английский, несет log23 бит информации, а что Иванов изучает французский – 1 бит. Сколько студентов изучают немецкий язык?
Y– учат французский
X– учат английский, 12 не учат английский. Всего 12+Xстудентов
Источник: studfile.net