Какие непрерывные объекты можно ввести в программе моделирования

Непрерывное Моделирование относится к компьютерной модели физической системы, которая непрерывно отслеживает системный ответ согласно ряду уравнений, как правило, включающих отличительные уравнения.

История

Это известно как одно из первого использования, когда-либо помещенного в компьютеры, отнесясь ко времени Eniac в 1946. Непрерывное моделирование позволяет предсказание

• траектории ракеты
• динамика водородной бомбы (N.B. это — первое использование, когда-либо помещенное в Eniac)

• моделирование электрической цепи
• робототехника

Установленный в 1952, Общество Modeling and Simulation International (SCS) является некоммерческой, управляемой волонтерами корпорацией, посвященной продвижению использования моделирования https://ru.knowledgr.com/08843759/%D0%9D%D0%B5%D0%BF%D1%80%D0%B5%D1%80%D1%8B%D0%B2%D0%BD%D0%BE%D0%B5%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5″ target=»_blank»]ru.knowledgr.com[/mask_link]

Моделирование физических систем: 09. Непрерывная САУ

Непрерывное моделирование

Непрерывное моделирование — это моделирование системы по времени с помо­щью представления, в котором переменные состояния меняются непрерывно по отношению ко времени. Как правило, в непрерывных имитационных моделях ис­пользуются дифференциальные уравнения, которые устанавливают отношения для скоростей изменения переменных состояния во времени. Если дифференци­альные уравнения очень просты, их можно решать аналитически, чтобы предста­вить значения переменных состояния для всех значений времени как функцию значений переменных состояния в момент времени 0. При больших непрерывных моделях аналитическое решение невозможно, но для численного интегрирования дифференциальных уравнений в случае с заданными специальными значениями для переменных состояния в момент времени 0 используются технологии числен­ного анализа, например интегрирование Рунге-Кутта.

Пример 1.3. Рассмотрим непрерывную модель соперничества между двумя популяция­ми. Биологические модели такого типа, именуемые моделями хищник-добыча (или па­разит-хозяин), рассматривались многими авторами, в том числе Брауном и Гордоном. Среда представлена двумя популяциями -хищников и добычи, взаимодействующими друг с другом.

Добыча пассивна, но хищни­ки зависят от ее популяции, поскольку она является для них источником пищи. (Напри­мер, хищниками могут быть акулы, а добычей — рыба, которой они питаются) Пусть x(t) и y(t) обозначают численность особей в популяциях соответственно добычи и хищников в момент времени t. Допустим, популяция добычи имеет обильные запасы пищи; при отсутствии хищников темп ее прироста составит r х(t) для некоторого положительного значения r (r — естественный уровень рождаемости минус естествен­ный уровень смертности). Существование взаимодействия между хищниками и добы­чей дает основание предположить, что уровень смертности добычи в связи с этим взаи­модействием пропорционален произведению численностей обоих популяций х(t)у(t). Поэтому общий темп изменения популяции добычи dx /dt: может быть представлен как

Полигональные объекты в КОМПАС-3D

где а — положительный коэффициент пропорциональности. Поскольку существование самих хищников зависит от популяции добычи, темп изменения популяции хищников в отсутствии добычи составляет -sу(t) для некоторого положительного s. Более того, взаимодействие между двумя популяциями приводит к росту популяции хищников, темп которого также пропорционален х(t)у(t). Следовательно, общий темп изменения популяции хищников dy/dt составляет

где b — положительный коэффициент пропорциональности. При начальных условиях х(0) > 0 и y(0) >0 решение модели, определенной уравнениями (1) и (2), имеет инте­ресное свойство: х(t) > 0 и у(t) > 0 для любого t³0. Следовательно, попу­ляция добычи никогда не будет полностью уничтожена хищниками. Решение также является периодической функцией времени.

Иными словами, существует такое значение Т> 0, при котором х(t + пТ)=x(t) и у(t + пТ) = у(t) для любого положительно­го целого числа п. Такой результат не является неожиданным. По мере увеличения по­пуляции хищников популяция добычи уменьшается. Это приводит к снижению темпа роста популяции хищников и, соответственно, вызывает уменьшение их числа, что, в свою очередь, ведет к увеличению популяции добычи и т. д.

Рассмотрим отдельные значения г = 0,001, а = 2 * 10 –6 ; s = 0,01; b=10 -6 , исходные разме­ры популяций составляют х( 0) = 12 000 и y(0) = 600. На рис. представлено числен­ное решение уравнений (1) и (2), полученное при использовании вычислительного пакета, разработанного для численного решения систем дифференциальных уравнений (а не языка непрерывного моделирования).

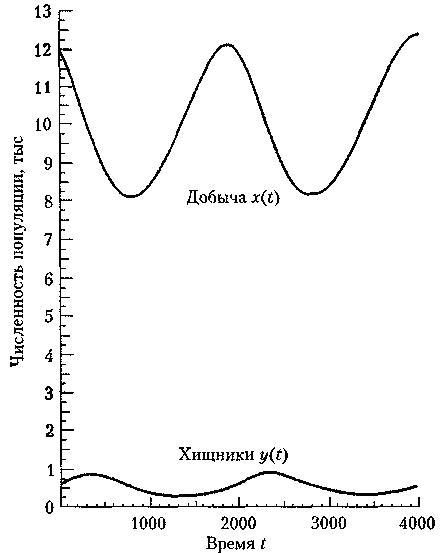
Обратите внимание на то, что приведенный выше пример полностью детерми­нистический, то есть в нем нет случайных компонентов. Однако имитационная модель может содержать и неизвестные величины; например, в уравнения (1) и (2) могут быть добавлены случайные величины, которые каким-то образом за­висят от времени, или постоянные множители могут быть смоделированы как ве­личины, случайно изменяющие свои значения в определенные моменты времени.

5.3 Комбинированное непрерывно-дискретное моделирование

Поскольку некоторые из систем невозможно отнести ни к полностью дискретным, ни к полностью непрерывным, может возникнуть необходимость в создании моде­ли, которая объединяет в себе аспекты как дискретно-событийного, так и непре­рывного моделирования, в результате чего получается комбинированное непрерыв­но- дискретное моделирование. Между дискретным и непрерывным изменениями переменных состояния могут происходить три основных типа взаимодействия:

— дискретное событие может вызвать дискретное изменение в значении не­прерывной переменной состояния;

— в определенный момент времени дискретное событие может вызвать изме­нение отношения, управляющего непрерывной переменной состояния;

— непрерывная переменная состояния, достигшая порогового значения, мо­жет вызвать возникновение или планирование дискретного события.

В следующем примере комбинированного непрерывно-дискретного моделиро­вания дано краткое описание модели, подробно рассмотренной Прицкером, который в своей работе приводит и другие примеры этого типа моделирования.

Пример 1.4. Танкеры, перевозящие нефть, прибывают в один разгрузочный док, попол­няя резервуар-хранилище, из которого нефть по трубопроводу попадает на нефтепере­гонный завод. Из разгружающегося танкера нефть подается в резервуар-хранилище с по­стоянной скоростью (Танкеры, прибывающие к занятому доку, образуют очередь.) На нефтеперегонный завод нефть подается из резервуара с различными заданными скорос­тями. Док открыт с 6.00 до 24.00. По соображениям безопасности разгрузка танкеров прекращается по закрытии дока.

Дискретными событиями в этой (упрощенной) модели являются прибытие танкера на разгрузку, закрытие дока в полночь и открытие в 6.00. Уровни нефти в разгружающемся танкере и резервуаре-хранилище задаются переменными непрерывного состояния, ско­рости изменения которых описаны с помощью дифференциальных уравнений.

Разгрузка танкера считается завершенной, когда уровень нефти в тан­кере составляет менее 5 % его емкости, но разгрузка должна быть временно прекращена, если уровень нефти в резервуаре-хранилище станет равным его емкости. Разгрузка мо­жет быть возобновлена, когда уровень нефти в резервуаре станет меньше 80 % его емко­сти.

В случае если уровень нефти в резервуаре станет меньше 5000 баррелей, нефтепере­гонный завод должен быть временно закрыт. Для того чтобы избежать частого закрытия и возобновления работы завода, подача нефти из резервуара на завод не будет возобнов­ляться до тех пор, пока в нем не наберется 50 000 баррелей нефти. Каждое из пяти собы­тий, связанных с уровнем нефти (например, падение уровня нефти ниже 5 % емкости танкера), по определению Прицкера, является событием состояния. В отличие от диск­ретных событий, события состояния не планируются, они происходят, когда перемен­ные непрерывного состояния переходят пороговое значение.

5.4 Моделирование по методу Монте-Карло. Статистическое моделирование систем

Источник: studopedia.su

32. Непрерывное моделирование

Непрерывное моделирование — это моделирование системы по времени с помо­щью представления, в котором переменные состояния меняются непрерывно по отношению ко времени. Как правило, в непрерывных имитационных моделях ис­пользуются дифференциальные уравнения, которые устанавливают отношения для скоростей изменения переменных состояния во времени. Если дифференци­альные уравнения очень просты, их можно решать аналитически, чтобы предста­вить значения переменных состояния для всех значений времени как функцию значений переменных состояния в момент времени 0. При больших непрерывных моделях аналитическое решение невозможно, но для численного интегрирования дифференциальных уравнений в случае с заданными специальными значениями для переменных состояния в момент времени 0 используются технологии числен­ного анализа, например интегрирование Рунге-Кутта.

33. Комбинированное непрерывно-дискретное моделирование

Поскольку некоторые из систем невозможно отнести ни к полностью дискретным, ни к полностью непрерывным, может возникнуть необходимость в создании моде­ли, которая объединяет в себе аспекты как дискретно-событийного, так и непре­рывного моделирования, в результате чего получается комбинированное непрерыв­но- дискретное моделирование. Между дискретным и непрерывным изменениями переменных состояния могут происходить три основных типа взаимодействия: — дискретное событие может вызвать дискретное изменение в значении не­прерывной переменной состояния; — в определенный момент времени дискретное событие может вызвать изме­нение отношения, управляющего непрерывной переменной состояния; — непрерывная переменная состояния, достигшая порогового значения, мо­жет вызвать возникновение или планирование дискретного события.

34. Моделирование по методу Монте-Карло.

Метод статистического моделирования (или метод Монте-Кар­ло) — это способ исследования поведения вероятностных систем в условиях, когда не извест­ны в полной мере внутренние взаимодействия в этих системах. Этот метод заключается в воспроизведении исследуемого физи­ческого процесса при помощи вероятностной математической мо­дели и вычислении характеристик этого процесса.

Одно такое вос­произведение функционирования системы называют реализацией или испытанием. После каждого испытания регистрируют сово­купность параметров, характеризующих случайный исход реализа­ции.

Метод основан на многократных испытаниях построенной модели с последующей статистической обработкой полученных данных с целью определения числовых характеристик рассматрива­емого процесса в виде статистических оценок его параметров. Авторами метода являются американские математи­ки Дж. Нейман и С. Улам.

Основой метода статистического моделирования является за­кон больших чисел. Закон больших чисел в теории вероятностей доказывает для различных условий сходимость по вероятности средних значений результатов большого числа наблюдений к неко­торым постоянным величинам. Под законом больших чисел понимают ряд теорем. Решение любой задачи методом статистического моделирования состоит в: разработке и построении структурной схемы процесса, выявле­нии основных взаимосвязей; формальном описании процесса; моделировании случайных явлений, сопровождающих функ­ционирование исследуемой системы;

моделировании функционирования системы–воспроизведении процесса в соответствии с разработанной структурной схемой и формальным описанием; накоплении результатов моделирования, их статистической об­работке, анализе и обобщении. Результаты, получаемые при статистическом моделировании, подвержены экспериментальным ошибкам. Экспериментальные ошибки при статистическом моделирова­нии в значительной степени зависят от точности моделирования случайных явлений, сопровождающих функционирование исследу­емой системы.

Источник: studfile.net