Линейные программы предназначены для изучения материала непосредственно на уроке, поскольку время работы с программой для студентов, имеющих различный уровень теоретической подготовки, примерно одинаково. [1]
Линейная программа — это программа, все операторы, которой выполняются строго последовательно в том порядке, как они записаны в тексте программы. [2]
Линейные программы с массивами составляются в соответствии с рассмотренным ранее правилом составления простейших программ, которое можно дополнить одним пунктом — после оператора КЕМ следует записать в программе оператор DIM. Кроме того, необходимо учитывать только что изложенные сведения о работе с массивами. [3]
Линейная программа — программа, команды которой исполняются машиной в порядке последовательности их записи. Реализация алгоритма поставленной задачи ( см. пример 14.1) с помощью линейной программы сводится к выполнению последовательности операций, представленных на рис. 14.2. В блоке 1 подготавливаются две переменные: одна — для накопления суммы г-х значений величины х и вычисления среднего значения xit а вторая — для подсчета числа этих значений, если заранее оно не известно. [5]
Линейная функция и ее график. 7 класс.
Линейная программа — программа, команды которой исполняются машиной в порядке последовательности их записи. [7]
Линейная программа — программа, команды которой исполняются в порядке последовательности их записи. Описание алгоритма с помощью символьной схемы также представляет последовательность символов, реализация которых осуществляется в порядке их следования. [8]
Линейные программы часто представляют в одной из следующих форм. [9]
Каждая линейная программа , в том числе и эта, имеет двойственную. Если исходная задача состоит в минимизации, то двойственная к ней — в максимизации и решение одной прямо приводит к решению другой; фактически минимум в данной основной задаче должен быть равен максимуму в двойственной к ней. [10]
Некоторые линейные программы имеют такую структуру, что их решение получается легко. [11]
Даже линейная программа обладает определенной структурой. [12]
Рассмотрим линейную программу ( в общих обозначениях гл. [13]
При линейной программе , если дается правильный ответ на контрольный вопрос, обучаемый переходит к изучению следующего-фрагмента информации. Если ответ обучаемого был неправильный, то ему рекомендуется возвратиться к повторению предыдущих фрагментов информации. При этом причины неправильных ответов, не вскрываются. Эту задачу решает сам обучаемый при повторении материала, на что он затрачивает определенное время. Это является основным недостатком линейной программы; достоинство ее заключается в простоте реализации в пособии. [14]
В линейной программе материал разбивается на маленькие порции ( дозы), которые последовательно ( линейно) предъявляются для изучения. В разветвленную программу ( см. рис. 36) вводятся дополнительные разъяснения в тех случаях, когда учащиеся ошибаются или затрудняются с ответами. Смешанная программа представляет собой комбинацию линейной и разветвленной. [15]
Линейные программы | Информатика Паскаль #8 | Инфоурок
Источник: www.ngpedia.ru
Линейное программирование: общие принципы
Линейное программирование — это математическая дисциплина, посвящённая теории и методам разрешения экстремальных задач на множествах многомерного векторного пространства, которые определяются системами линейных уравнений и неравенств.
Введение
Успешное разрешение фактически любой экономической проблемы зависит от выбора самого лучшего метода использования имеющихся ресурсных возможностей. В процессе экономической деятельности необходимо выполнять распределение таких важнейших ресурсов, как финансы, товары, сырьевые запасы, технические средства, рабочая сила и другое.
От оптимального распределения этих, как правило, не бесконечных ресурсных возможностей в конечном итоге зависят результаты деятельности. Смысл методов оптимизации заключается в том, чтобы на базе наличия определённых запасов ресурсов, определить самый лучший способ их использования или распределения, который обеспечивает самые лучшие параметры по требуемым показателям. При этом следует учитывать существующие ограничения, накладываемые на использование ресурсных возможностей существующей экономической ситуацией. Способами оптимизации в экономике, в научной и социальной сфере способны стать многие главные направления математического программирования, в частности, линейное, нелинейное и динамическое программирование.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Линейное программирование
Под линейным программированием понимаются методы математического моделирования, которые выработаны для оптимизации использования ограниченных ресурсных возможностей. Линейное программирование является наиболее простым и самым проработанным разделом математического программирования. Линейное программирование успешно применяется в оборонной промышленности, индустриальных областях и других сферах.
Повсеместное использование данных методов подкрепляется обширным набором программных алгоритмов, реализующих эти методы. Алгоритмы линейного программирования, при учёте их значительной эффективности, выступают в качестве основы оптимизационных алгоритмов для других, более сложных типов моделей и задач исследования операций, включая целочисленное, нелинейное и стохастическое программирование. Расчёты в методе линейного программирования, как и практически во всех задачах исследования операций, как правило, могут быть очень трудоёмкими и этот факт предопределяет применение вычислительной техники.
«Линейное программирование: общие принципы»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы
Линейное программирование служит для определения оптимального плана распределения ограниченных однородных ресурсов для решения поставленной задачи.
Приведём конкретный пример. Компания «Яркие краски» осуществляет производство красок для внутренних и наружных работ, применяя для этого сырьё двух типов: М1 и М2. Ниже приведена таблица, где представлены основные исходные данные задачи.
Рисунок 1. Исходные данные задачи. Автор24 — интернет-биржа студенческих работ
Маркетинговое подразделение компании установило ограничение на ежедневный выпуск краски для внутренних работ двумя тоннами по причине ограниченного спроса на неё, а также выдвинуло условие, что дневной выпуск краски для внутренних работ не может превышать больше чем на одну тонну выпуск краски для наружных работ. Компания хочет определить наилучшее соотношение между типами выпускаемой продукции, обеспечивающее самый большой общий каждодневный доход.
Задача линейного программирования, подобно всем другим задачам исследования операций, может состоять из следующих компонентов:
- Совокупность переменных, которые необходимо определить.
- Целевая функция, подлежащая оптимизации.
- Перечень ограничений, которым обязаны удовлетворять все переменные.
Определение переменных считается первым этапом в создании модели. Если выполнено определение всех переменных, то задание ограничений и выработка целевой функции, обычно, может считаться несложной проблемой.
Для указанного примера нужно определить ежедневные объёмы выпуска краски для внутренних и наружных работ. Выберем следующие обозначения:
- X1 является переменной, которая определяет ежедневный выпуск краски для наружных работ, задаваемый в тоннах.
- X2 является переменной, которая определяет ежедневный выпуск краски для внутренних работ, измеряемый тоже в тоннах.
Затем, на основе введённых переменных, необходимо найти целевую функцию. Очевидно, что в нашем варианте целевой функцией может считаться общий ежедневный доход, который обязан возрастать при увеличении объёма выпускаемых красок. Зададим следующие обозначения:
Z является целевой функцией, которая определяет общий ежедневный доход и должна измеряться в тысячах долларов.
В соответствии с условиями рассматриваемого примера, целевая функция может быть представлена следующей формулой:
Далее согласно поставленной задаче и целям компании, необходимо определить условия, которые обеспечивают максимум целевой функции. Для этого необходимо определить последний элемент модели, то есть, ограничения, которые учитывают имеющиеся возможности ежедневного использования сырья и уровень спроса на уже готовую продукцию. В соответствии с таблицей, в которой представлены исходные данные, имеем:
- М1 = 6Х1 + 4Х2 (т) используемый сырьевой объём.
- М2 = 1Х1 + 2Х2 (т) используемый сырьевой объём.
Так как дневной расход сырья М1 и М2 ограничен указанными выше объёмами, то можно определить следующие ограничения:
- 6Х1 + 4Х2 ≤ 24 для сырья М1.
- Х1 + 2Х2 ≤ 6 для сырья М2
Существуют ещё два ограничения, задаваемые объёмом спроса на готовую продукцию:
- Максимальный дневной объём выпуска краски для внутренних работ не должен превышать две тонны.
- Дневной объём выпуска краски для внутренних работ не должен превышать дневной объём выпуска краски для наружных работ более чем на тонну.
Первое ограничение может быть записано так:
Второе ограничение может быть представлено как разность между дневными объёмами выпуска красок для внутренних и наружных работ, которая должна быть менее тонны, то есть:
Любое решение, удовлетворяющее модельным ограничениям, станет допустимым. Так решением может быть Х1 = 3 и Х2 = 1, и оно является допустимым. Такая задача может иметь бесконечное множество решений, то есть максимальное значение данной целевой функции нельзя найти простым перебором допустимых решений.
Источник: spravochnick.ru
Кратко о линейном программировании
Итак, линейное программирование возникло после Второй мировой войны и стал быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а так же математической «стройности».
Можно сказать, что линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр.
Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
· рационального использования сырья и материалов; задачи оптимизации раскроя;
· оптимизации производственной программы предприятий;
· оптимального размещения и концентрации производства;
· составления оптимального плана перевозок, работы транспорта;
· управления производственными запасами;
· и многие другие, принадлежащие сфере оптимального планирования.
Так, по оценкам американских экспертов, около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.
Первые постановки задач линейного программирования были сформулированы известным советским математиком Л.В.Канторовичем, которому за эти работы была присуждена Нобелевская премия по экономике.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения.
Итак, линейное программирование — это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции.
1.3 Основная задача линейного программирования
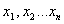
Основная задача линейного программирования (ОЗЛП) ставится следующим образом: Имеется ряд переменных . Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:
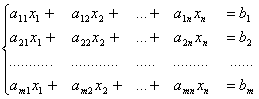
и, кроме того, обращали бы в минимум линейную целевую функцию (ЦФ)
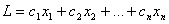
Очевидно, случай, когда ЦФ нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию
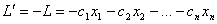
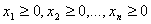
Допустимым решением ОЗЛП называют любую совокупность переменных , удовлетворяющую уравнениям (1.1).
Оптимальным решением называют то из допустимых решений, при котором ЦФ обращается в минимум.
На практике ограничения в задаче линейного программирования часто заданы не уравнениями, а неравенствами. В этом случае можно перейти к основной задаче линейного программирования.
Рассмотрим задачу линейного программирования с ограничениями-неравенствами, которые имеют вид
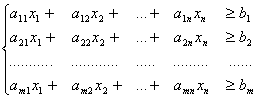
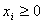
и являются линейно-независимыми. Последнее означает, никакое из них нельзя представить в виде линейной комбинации других. Требуется найти , которые удовлетворяют неравенствам и обращают в минимум
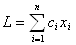
где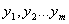 
— добавочные переменные, которые также как и 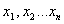являются неотрицательными.
Таким образом, имеем общую задачу линейного программирования — найти неотрицательные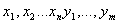 
, чтобы они удовлетворяли системе уравнений (1.3) и обращали в минимум .
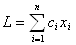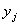
Коэффициенты в формуле (1.3) перед равны нулю.
Информация о работе «Решение задачи линейного программирования графическим методом»
Раздел: Информатика, программирование
Количество знаков с пробелами: 40640
Количество таблиц: 2
Количество изображений: 10
Источник: kazedu.com