SMath Studio является математическим редактором, позволяющим производить разнообразные научные и инженерные расчеты. Его автор – российский программист – Андрей Ивашов, официальный сайт предлагаемого им проекта: http://smath.info .
SMath Studio очень прост в использовании из-за отсутствия необходимости сначала писать программу, а потом запускать ее на исполнение. Вместо этого достаточно вводить математические выражения с помощью встроенного редактора формул в виде, максимально приближенном к общепринятому, и тут же получать результат.
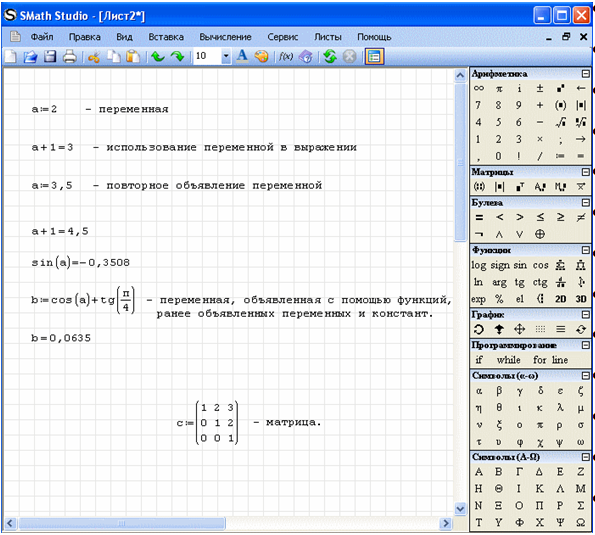
SMath Studio имеет основное рабочее поле, в котором производятся все вычисления. При стандартных настройках оно выглядит как тетрадный лист в клетку, и в нем, как на тетрадном листе, пользователь вводит математические выражения. Для этого надо установить курсор (красный крестик) в понравившееся место и начать ввод с клавиатуры (рис. 1.1). Как видно, окно программы стандартно содержит заголовок, главное меню, панель инструментов и само рабочее поле:
Интерактивная сенсорная панель
После того, как выражение введено, можно его посчитать, нажав «=». Похожим способом объявляется переменная: пишется имя, ставится знак присваивания «:=» с помощью кнопки на панели «Арифметика» или двоеточием на клавиатуре, вводится значение. Объявленную переменную можно использовать в выражениях, ее значение будет подставлено автоматически при вычислениях. Если навести курсор мыши на невыделенное выражение, то появится его результат в символьной форме.
Реакция программы на нажатие некоторых клавиш зависит от контекста. В таблице 1.1 приведены наиболее частые варианты.
Таблица 1.1 — Изменение реакции на клавиши
Вставка «#» в рабочем поле листа, выделение большей части выражения при уже выделенной угловым курсором части, пробел для текстового поля.
Вставка пустого промежутка на листе, выход из поля выражения.
Переход к следующему или предыдущему выражению, движение по элементам выражения с изменением углового курсора.
Корень квадратный в рабочем поле листа или обратный слэш в тексте.
Дробь в рабочем поле листа или прямой слэш в тексте.
В текстовом поле это так и останется двоеточием, а в рабочем поле листа превратится в знак присваивания.
Знак равно в тексте и команда численного вычисления в поле формулы. Для попытки вычисления необъявленной переменной буде произведена замена на «:=».
Shift+2. «Собака» в тексте на английской раскладке или двумерный график в рабочем поле листа.
В тексте это будет выглядеть так же, а при вводе формулы станет местом для нижнего индекса.
Внешний вид запущенной программы с объявленными переменными показан на рисунке 1.2.
Задание. Изучите назначение кнопок панели инструментов:
Положительные и отрицательные обратные связи в системе управления.
Составьте отчет в виде таблицы.
Кнопка панели инструментов
У SMath Studio есть некоторые правила записи выражений:
- Используемая переменная или функция должна быть объявлена заранее. Заранее – значит левее или выше того выражения, где она используется в вычислении.
- Если переменная переобъявлялась, то будет использовано то значение, которое встретилось самым последним перед использованием в вычислениях.
- При объявлении переменной в выражении можно использовать встроенные и ранее объявленные функции, ранее объявленные переменные и их сочетания. Если используемые в выражении переменные ранее не объявлялись, то результат можно будет получить только в символьном виде (или объявить недостающие переменные и разместить выражение ниже или правее объявленных переменных для численного результата).
- Переменная не обязательно должна вычисляться как числовое значение, допускается присваивать имена выражениям, дающим при вычислении матрицу.
- Для символьных вычислений объявлять переменные заранее не требуется, если не надо, чтобы при преобразовании выражений были подставлены их значения.
Справа в окне программы расположена Боковая панельинструментов, она может быть убрана нажатием на крайнюю правую кнопку 
главной панели инструментов. Боковая панель состоит из отдельных панелей, содержащих наборы команд в виде кнопок. Каждая такая панель может быть свернута с помощью кнопки 
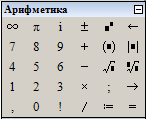Рисунок 1.3 Панель «Матрицы» (рис. 1.4) позволяет задать матрицу (Ctrl+«M»), вычислить ее определитель, транспонировать матрицу, получить алгебраическое дополнение, минор, вычислить векторное произведение. Вектор задается как вектор-столбец (т.е. матрица) с размером в 3 элемента, по одному на каждой строке. 
Рисунок 1.4 Панель «Булева» (рис. 1.5) содержит операции отношения, отрицание, «и», «или», «исключающее или». Булево «равно» используется еще и в задании условий для функции if и в цикле for. 
Рисунок 1.5 Панель «Функции» (рис.1.6) содержит подборку основных тригонометрических функций, определенный интеграл, производную, сумму элементов и их произведение. Еще есть логарифм по произвольному основанию, натуральный логарифм, проценты, выбор элемента по индексу («el» или квадратные скобки на клавиатуре), знак системы. 
Рисунок 1.6 Например, результат работы функции дифференцирования (кнопка 
) зависит от того, выбрано ли вычисление значения производной в точке при помощи «=» или использовано символьное вычисление «→» (рис. 1.7).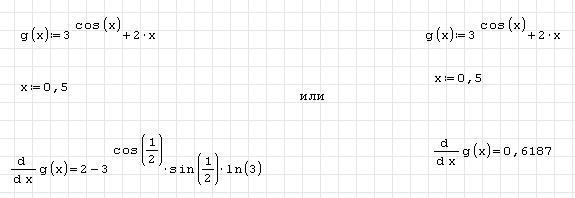 
Рисунок 1.7 Панель «График». Здесь можно вращать, масштабировать и сдвигать графики, задавать отображение точками или линиями, перерисовывать графики заново в случае необходимости. Операция вращения доступна только для трехмерных графиков. Графики рисуются в декартовой системе координат (рис.1.8). 
Рисунок 1.8 Графики строятся для функций от переменной «x» (2D) или «x» и «y» (3D). Вообще, функции могут быть от любых аргументов, но при построении графика должны быть указаны в качестве аргументов именно эти переменные (рис.1.9). 
Рисунок 1.9 Помимо аналитического задания графика, можно задать его в виде матрицы (рис. 1.10), где каждый столбец будет содержать координаты точек для осей X и Y соответственно (или еще для оси Z). 
Рисунок 1.10 Кроме того, вместо функции или матрицы можно поставить знак системы, а уже в систему вписать имена функций или матриц или выражения для построения графиков. Это позволит отобразить несколько графиков на одном рисунке (рис. 1.11).
 |
 |
 |
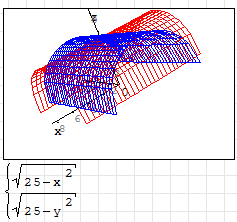| Рисунок 1.11 | ||
Панель «Программирование» (рис. 1.12) содержит средства, позволяющие организовать циклические вычисления (циклы «for» и «while») или задать условную функцию «if». Вместо операторных скобок используется линия (line). Линия по умолчанию содержит два места для последовательных вычислений, но ее можно растянуть. Для этого выделите линию угловым курсором (надо кликнуть по месту, отмеченному квадратиком и нажать пробел, чтобы выделились оба места). Должна появиться специальная квадратная метка, зацепив которую мышкой, можно растянуть линию до необходимого количества мест. Аналогичный способ растягивания работает и для знака системы. 
Рисунок 1.12 Панели «Символы» (рис. 1.13) нужны для вставки букв греческого алфавита. 
Рисунок 1.13 SMath Studio может использоваться в качестве инженерного калькулятора (рис. 1.14). Как калькулятор SMath Studio сможет оперировать переменными, делать символьные вычисления, искать корни уравнения по переменной, упрощать выражения и т.д. Примеры использования SMath Studio можно найти на сайте http://smath.info .
 |
 |
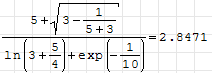| Рисунок 1.14 | |
Набор функций на одноименной панели SMath Studio весьма ограничен. Меню «Вставка» позволяет использовать и другие встроенные функции, причем их достаточно много (рис. 1.15). Функции сгруппированы по разделам. Щелчок мышью в списке «Имя функции» и нажатие буквенной клавиши покажут функцию, начинающуюся с этой буквы. 
Рисунок 1.16 «Вычисление» содержит целый набор возможных действий (рис. 1.17). Выделив выражение или его часть, можно найти вещественные корни уравнения, произвести вычисления с учетом подстановок и сокращений, упростить выражение, получить обратное значение в символьном или числовом виде, получить производную по выделенной заранее переменной и определитель матрицы. 
Рисунок 1.17 «Сервис» содержит такой пункт, как «Опции» (рис. 1.18). Он служит для задания точности представления результата, диапазона поиска корней уравнений, а также для настройки внешнего вида программы, включая цвета и язык и т.п.
 |
 |
| Рисунок 1.18 | |
«Помощь» открывает доступ к справочнику, сообщает сведения о программе (сборка, авторы, контактная информация, используемые библиотеки), проверяет наличие обновлений программы через Интернет и сообщает о способах финансовой поддержки проекта. Отдельно следует упомянуть пункт «Примеры» (рисунок 1.19). В нем показано как можно, используя программирование, выполнять вычисления, для которых нет встроенных функций. 
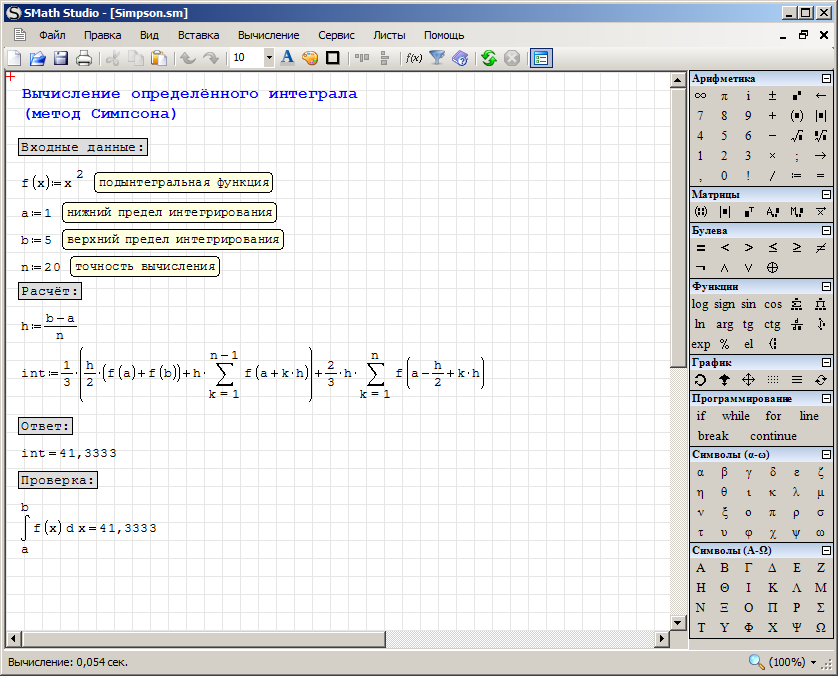Рисунок 1.20 Задание. Изучите подпункт «Справочник» пункта главного меню «Помощь». Составьте подробный отчет. Как и у всякой сложной программы, у SMath Studio есть особенности:
- Выделение кликом мышки служит для редактирования формулы, текста или вида графика, а выделение рамкой – для перетаскивания, копирования и удаления объектов на листе.
- Знак равенства служит для вычисления, а знак «жирное равно» – для задания условия равенства в уравнениях, циклах и в условной функции.
- Для поиска корней уравнений задается определенный диапазон.
- Интеграл берется по действительным (вещественным) пределам интегрирования.
12
Источник: studfile.net
Smath Studio Руководство пользователя. Руководство пользователя
Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма
Скачать 1 Mb.
Глава 10 Встроенные функции
10.1 Вставка встроенных функций
Особенности вставки функций
Чтобы видеть список встроенных функций, доступных в SMath Studio, расположенных в алфавитном порядке или по категориям, или вставить функцию вместе с метками-заполнителями для ее аргументов, используют диалоговое окно Вставка-Функция:
1. Щелкните в незаполненной области вашего рабочего листа или на метке-заполнителе
2. Выберите пункт Функция из меню Вставка или нажмите на значок на панели инструментов.
SMath Studio открывает диалоговое окно Вставка-Функция.
3. Щелкните на нужную категорию функции или щелкните “Все”, чтобы видеть все доступные функции, отсортированные в алфавитном порядке.
4. Щелкните два раза по названию функции, которую вы хотите вставить из правого списка, или щелкните «Вставить». Функция и метки-заполнители для ее аргументов будут вставлены в рабочий лист.
5. Заполните метки-заполнители
Чтобы применить функцию к выражению, в которое вы уже вошли, помещаете выражение между двумя линиями редактирования и следуете за шагами, данными выше. См. главу 4, “Работа с математикой,” для информации об использовании линий редактирования.
Вы можете также просто ввести имя встроенной функции непосредственно в метку- заполнитель или в математическую область.
Совет
Имена встроенных функций учитывают регистр. Если вы не используете диалоговое окно Вставка-Функция, чтобы вставить имя функции, вы должны
ввести имя встроенной функции в математической области точно так же, как это появляется в таблицах всюду по этой главе: прописные буквы, строчные буквы, или смешанные, как обозначено
Помощь для использования встроенных функций
Вызов диалогового окна Вставка-Функция дает вам удобный способ искать функцию по категориям, видеть аргументы, требуемые, и видеть краткое описание функции. Быстрые примеры, которые позволяют полнее понять применение функции, на данный момент в
SMath Studio отсутствуют.
10.2 Базовые математические функции
Тригонометрические функции
arcos(z)
Возвращает угол (в радианах), чей косинус – z.
arccosec(z)
Возвращает угол (в радианах), чей косеканс – z.
arcctg(z)
Возвращает угол (в радианах), чей котангенс – z.
arcsec(z)
Возвращает угол (в радианах), чей секанс – z.
arcsin(z)
Возвращает угол (в радианах), чей синус – z.
arctg(z)
Возвращает угол (в радианах), чей тангенс – z.
cos(z)
Возвращает косинус z. В прямоугольном треугольнике это отношение длины прилежащего катета к длине гипотенузы.
cosec(z)
Возвращает
1/sin z
, косеканс z. ctg(z)
Возвращает котангенс z. sec(z)
Возвращает
1/cos z
, секанс z.
sin(z)
Возвращает синус z. В прямоугольном треугольнике это отношение длины противолежащего катета к длине гипотенузы.
tg(z)
Возвращает тангенс z. В прямоугольном треугольнике это отношение длины стороны противолежащего катета к длине стороны прилежащего катета.
Тригонометрические функции SMath Studio и обратные им функции принимают любой скалярный аргумент: действительный, комплексный, или мнимый. Они также возвращают комплексные числа везде, где это необходимо.
Замечание Тригонометрические функции ожидают свои аргументы в радианах. Чтобы передать аргумент в градусах, используйте встроенную единицу deg (градус).
Например, чтобы вычислить синус 45 градусов, напечатайте sin (45*deg).
Гиперболические функции
arch(z)
Возвращает число, гиперболический косинус которого – z.
arcth(z)
Возвращает число, гиперболический котангенс которого – z.
arsh(z)
Возвращает число, гиперболический синус которого – z.
arth(z)
Возвращает число, гиперболический тангенс которого – z.
ch(z)
Возвращает гиперболический косинус z.
cosech(z)
Возвращает
1/sh z
, гиперболический косеканс z.
cth(z)
Возвращает
1/th z
, гиперболический котангенс z.
sech(z)
Возвращает
1/ch z
, гиперболический секанс z.
sh(z)
Возвращает гиперболический синус z.
th(z)
Возвращает
shz /ch z
, гиперболический тангенс z.
Логарифмические и экспоненциальные функции
Данные типы функций в SMath Studio не выделены в отдельную категорию, их необходимо искать в категории “Все” exp(z)
Возвращает величину e, возведенную в степень z.
ln(z)
Возвращает натуральный логарифм z.
lg(z)
Возвращает десятичный логарифм z.
log(a;b)
Возвращает логарифм от a по основанию b.
Экспоненциальные и логарифмические функции SMath Studio могут принять и возвратить комплексные аргументы.
Комплексные числа
arg(z)
Возвращает угол в комплексной плоскости от действительной оси до z.
Результат между - и радианами.
Im(z)
Возвращает мнимую часть числа z pol2xy(a;b) Функция перевода координат точки с координатами (a;b) из полярной системы в прямоугольную.
Re(z)
Возвращает вещественную часть числа z xy2pol(a;b) Функция перевода координат точки с координатами (a;b) из прямоугольной системы в полярную.
Кусочно-непрерывные функции
Данные типы функций в SMath Studio не выделены в отдельную категорию, их необходимо искать в категории “Все” sign(z)
Возвращает 0, если z = 0, 1, если z>0 и -1, если z Функции округления, усекания и вычисления остатка
Данные типы функций в SMath Studio не выделены в отдельную категорию, их необходимо искать в категории “Все”
mod(x;n)
Возвращает остаток от деления вещественного числа x на целое число n round(x;n)
Вещественное число x округляется до n знаков после запятой. Если n=0, x возвращается, округленный к ближайшему целому числу trunc(x)
Возвращает целую часть вещественного числа x, удаляя дробную часть.
Функции возведения в степень
sqrt(x)
Возвращает значение квадратного корня из числа x nthroot(n;x) Возвращает корень степени n из числа x
Специальные функции
Данные типы функций в SMath Studio не выделены в отдельную категорию, их необходимо искать в категории “Все”
error(«строка»)
Отображает текст в виде стандартной ошибки SMath Studio.
eval(arg)
Переводит выражение arg, представленное аналитически, в численный вид
IsDefined(arg)
Возвращает 1, если все переменные и функции для выражения arg определены, в противном случае возвращает 0.
Gamma(z)
Возвращает значение классической Эйлеровой гамма-функции для z, в виде вещественного или комплексного числа. Неопределена для z0
perc(x;n)
Возвращает проценты, заданные величиной n, от числа x
10.3 Векторные и матричные функции
Отметьте, что данные функции ожидают, что векторы всегда будут векторы-столбцы, а не векторы-строки. Чтобы преобразовать вектор-строку в вектор-столбец, используйте оператор транспонирования.
Размер и область действия матриц
cols(A)
Возвращает число столбцов в матрице A. Если A скаляр, выдает ошибку.
length(A)
Возвращает общее количество элементов вектора или матрицы A.
max(A)
Возвращает максимальный элемент заданного вектора или матрицы. Если встречается комплексный элемент, функция возвращает комплексное число, составленное из максимальной встретившейся действительной части плюс максимальной встретившейся мнимой части.
min(A)
Возвращает минимальный элемент заданного вектора или матрицы. Если встречается комплексный элемент, функция возвращает комплексное число, составленное из минимальной встретившейся действительной части плюс минимальной встретившейся мнимой части.
rows(A)
Возвращает число строк в матрице A. Если A скаляр, выдает ошибку.
Специальные типы матриц
diag(v)
Возвращает матрицу на главной диагонали которой элементы вектора v.
identity(n)
Возвращает единичную матрицу указанного порядка n.
Специальные характеристики матриц
alg(A;n;m)
Возвращает алгебраическое дополнение матрицы А (минор матрицы, взятый со знаком, зависящим от номера строки n и столбца m)
det(A)
Возвращает определитель матрицы (детерминант).
minor(A;n;m) Возвращает минор матрицы А (определитель n-1-го порядка, полученный из матрицы А вычеркиванием n-ой строки и m-го столбца)
norm1(A)
Возвращает норму матрицы в пространстве L1.
norme(A)
Возвращает евклидову норму матрицы.
normi(A)
Возвращает равномерную норму матрицы.
rank(A)
Ранг матрицы tr(A)
След матрицы.
Формирование новых матриц
augment(A;B;C. )
Функция возвращает массив образованный последовательным размещением аргументов друг рядом с другом (слева направо).
Аргументы могут быть скалярами, векторами или матрицами с одинаковым количеством столбцов.
Jacob(A;B)
Функция возвращает квадратную матрицу частных производных функций нескольких переменных, являющихся элементами вектора
А по переменным, являющимися элементами вектора B. Пример использования приведен на рис. 10.1
invert(A)
Определение обратного значения матрицы A
matrix(n;m)
Возвращает нулевую матрицу размером nm.
stack(A;B;C. )
Функция возвращает массив образованный последовательным размещением аргументов друг под другом. Аргументы могут быть скалярами, векторами или матрицами с одинаковым количеством столбцов.
submatrix(A;ir;jr;ic;jc)
Возвращает субматрицу A, состоящего из всех элементов, содержавшихся в строках от ir до jr и столбцах от ic до jc. transpose(A)
Функция производит транспонирование матрицы или вектора.
wminor(A;n;m)
Функция возвращает матрицу, сформированную путем исключения строки n и столбца m из матрицы А.
Рисунки 10.1 и 10.2 показывает примеры использования функций Jacob, stack и augment.
Рис. 10.1 Использование функции Jacob
Рис. 10.2 Соединение матриц с использованием функций stack и augment
Функции операций с частями матриц или векторов
col(A;n)
Возвращает n-ый столбец матрицы или вектора А.
el(A;n)
Возвращает n-ый элемент вектора А.
el(A;n;m)
Возвращает элемент матрицы А по указанной строке n и столбцу m.
row(A;m)
Возвращает m-ую строку матрицы или вектора А.
Функции сортировки
csort(A;n)
Возвращает матрицу/вектор с элементами, отсортированными по указанному столбцу n в порядке возрастания.
reverse(A)
Изменяет порядок строк матрицы или элементов вектора на противоположный.
rsort(A;n)
Возвращает матрицу/вектор с элементами, отсортированными по указанной
строке в порядке возрастания.
sort(A)
Возвращает вектор с элементами, отсортированными в порядке возрастания.
10.4 Функции решения уравнений
Этот раздел описывает, как решить уравнения в диапазоне от единственного уравнения с одним неизвестным до больших системам со множеством неизвестными.
Методы, описанные здесь, производят численные решения. Глава 14 “Символьное вычисление” описывает множество методов для того, чтобы решить уравнения символически.
Нахождение корней
polyroots(v)
Возвращает корни полинома, заданного вектором его коэффициентов.
solve(f(z);z)
Возвращает действительные корни уравнения f(z) относительно указанной переменной z.
solve(f(z);z;a;b)
Возвращает действительные корни уравнения f(z) внутри промежутка между a и b относительно указанной переменной z.
Функция solve решает одно уравнение с одним неизвестным. Уравнение может быть как линейным, так и нелинейным. Для данной функции возможно задание диапазона, в котором следует искать корни уравнения.
Совет Вы можете изменить диапазон, в котором SMath Studio будет искать корни при решении систем уравнений. Для этого нужно вызвать диалоговое окно Опции , выбирая пункт Опции из меню Сервис, и задать требуемый диапазон корней.
Чтобы найти корни многочлена или выражения, имеющего форму:
v
n
x
n
. v
2
x
2
v
1
x
1
v
вы можете использовать функцию polyroots. Эта функция не требует начального приближения и возвращает корни сразу, действительные или комплексные. Рисунок 10.3 показывает примеры использования функций solve и polyroots.
Решение линейных/нелинейных систем уравнений
SMath Studio включает числовые функции решения, которые могут решать задачи следующих типов:
•
Линейные системы уравнений;
•
Нелинейные системы уравнений;
Для решения вышеперечисленных задач можно использовать функцию roots. Примеры использования данной функции для решения систем уравнений приведены на рис. 10.4.
roots(f(z);z)
Нахождение корней системы нелинейных уравнений. Возвращает значения в векторе z, при которых функции вектора f(z) равны нулям.
roots(f(z);z;z
)
Нахождение корней системы нелинейных уравнений с учётом указанных приближений в векторе z
. Возвращает значения в векторе z, при которых функции вектора f(z) равны нулям.
Рис. 10.3 Нахождение корней с помощью функций solve и polyroots
Рис. 10.4 Решение систем уравнений с помощью функции roots
Так же как и в предыдущем разделе, для решения систем уравнений можно задавать диапазоны, в которых находятся корни.
10.5 Функции распределения вероятности и анализа данных
Распределение вероятности
В SMath Studio входит одна из функций распределения вероятности – генератор случайных чисел. Его описание дано ниже.
random(n)
Возвращает случайно выбранное число в диапазоне от 0 до n.
Функции интерполяции
Замечание
Всякий раз, когда вы используете векторы или матрицы в любой из функций, описанных в этом разделе, убедитесь, что каждый элемент вектора или матрицы содержит значение данных. SMath Studio назначает 0 на любые элементы, которые вы явно не назначили.
ainterp(vx;vy;x) Возвращает интерполированное сплайном Акимы значение для значения x, используя данные из вектора аргумента vx и вектора функций vy. Вектора должны иметь одинаковые размеры.
cinterp(vx;vy;x) Возвращает интерполированное кубическим сплайном значение для значения x, используя данные из вектора аргумента vx и вектора функций vy. Вектора должны иметь одинаковые размеры.
linterp(vx;vy;x) Возвращает линейно интерполированное значение для значения x, используя данные из вектора аргумента vx и вектора функций vy. Вектора должны иметь одинаковые размеры.
Интерполяция использует существующие частные значения, чтобы предсказать значения между этими частными значениями. SMath Studio позволяет вам соединять частные значения либо отрезками прямых (линейная интерполяция), либо отрезками кубического многочлена (кубическая интерполяция сплайна). Эти функции интерполяции возвращают кривую, которая должна пройти через точки, которые вы определяете.
Интерполяция кубическим сплайном представляет кривую через ряд точек таким способом, при которым первые и вторые производные кривой непрерывны в любой исходной точке. Эта кривая получена взятием трех смежных точек и построением кубического многочлена, проходящего через эти точки. Эти кубические многочлены собраны вместе, чтобы сформировать законченную кривую.
Пример использования функций cinterp и linterp показан на рис. 10.5.
Рис. 10.5 Использование функций cinterp и linterp
10.6 Прочие функции
Функции работы со строками
concat(s1;s2;s3. ) Возвращает строку образованную последовательным сцеплением подстрок s1,s2,s3. указанных аргументами функции.
error(s)
Отображает текст в виде стандартной ошибки SMath Studio.
findstr(s1;s2)
Возвращает вектор индексов положения подстроки s2 в указанной строке s1 или -1, если подстрока не была найдена.
IsString(s)
Возвращает 1, если указанный аргумент строка. В противном случае 0.
num2str(s)
Преобразовывает математическое выражение s в строку.
str2num(s)
Возвращает математическое выражение, сформированное преобразованием из заданной строки s.
strlen(s)
Возвращает количество символов указанной строки s.
strrep(s1;s2;s3)
Заменяет все вхождения строки s2 на строку s3 в тексте s1.
substr(s1;s2)
Возвращает подстроку из s1, где s2 показывает стартовую позицию итоговой строки.
substr(s1;s2;s3)
Возвращает подстроку из s1, где s2 показывает стартовую позицию итоговой строки, а «3:число»s3 .
importData(s)
Возвращает матрицу данных, загруженных из файла s используя настройки импорта по умолчанию.
Строки, используются и возвращаются в результате использования большинства этих функций, печатаются в математической метке-заполнителе, нажимая клавишу кавычек («) и вводя любую комбинацию символов, чисел, или других цифр ASCII. SMath Studio автоматически помещает двойные кавычки вокруг строкового выражения и показывает кавычки вокруг строки, возвращенной в результате работы функции.
Замечание
Вызывая функции findstr и substr, SMath Studio предполагает, что первый символ в строке имеет порядковый номер 1.
Функции доступа к файлам
Аргумент файла, который вы подставляете в функцию доступа к файлу SMath Studio, является строкой или переменной, которой назначена строка, и может быть любым из:
•
имя файла данных или файла изображения в папке рабочего листа SMath Studio, с которым вы в настоящее время продолжаете работать;
•
полный или относительный путь к файлу данным, расположенному в другом месте на местной файловой системе или файловой системе сети.
Чтение ASCII файла данных
importData(s)
Возвращает матрицу данных, загруженных из файла s используя настройки импорта по умолчанию.
importData(9)
Возвращает матрицу данных, загруженных из файла. Функция может быть использована с любым количеством аргументов в диапазоне 1-9. Цифра 0
(ноль) может быть использована в аргументах (кроме первого ‘имяФайла’) для применения значений поумолчанию.
Файлы в простом формате ASCII состоят только из чисел, отделенных запятыми, пробелами, или переводами строк. Числа в файлах с данными могут быть целыми числами как 3 или -1, числами с плавающей точкой как 2.54 или числами с мантиссой как 4.51Е-4.
Операции с файлами
dfile(s)
Безвозвратно удаляет файл с именем s, который содержит в себе математическое выражение, если таковой существует. Если операция прошла удачно, то функция возвращает ‘1’, иначе ‘0’.
rfile(s)
Возвращает прочитанное математическое выражение из файла s, если такой существует.
rfile(s1;s)
Записывает в файл s выражение s1. Если файл с указанным названием уже существует, функция перепишет его новым значением. Если операция прошла удачно, будет возвращено ‘1’, в противном же случае ‘0’.
Источник: topuch.com
Презентация на тему SMath Studio
SMath Studio http://smath.ru бесплатная или условно-платная (по желанию) программа с удобным интерфейсом; поддержка пользователей, организованная через форум; тестирование и частичная отладка силами пользователей; получение бесплатных консультаций от разработчиков по возможностям
Слайды и текст этой презентации
Слайд 1SMath Studio
Переверзев Владимир Юрьевич,
зав. лабораторией НИИРПО,
к.п.н, доцент
Слайд 2SMath Studio http://smath.ru
бесплатная или условно-платная (по желанию)
программа с удобным интерфейсом;
поддержка пользователей, организованная через
форум;
тестирование и частичная отладка силами пользователей;
получение бесплатных консультаций от разработчиков по возможностям программы на форуме;
широкий набор выполняемых действий (вычисления функций, построение графиков, работа с матрицами, вычисление определенных интегралов, численное и символьное дифференцирование и многое другое)
Слайд 3SMath Studio окно программы содержит заголовок, главное меню,
панель инструментов и само рабочее поле.
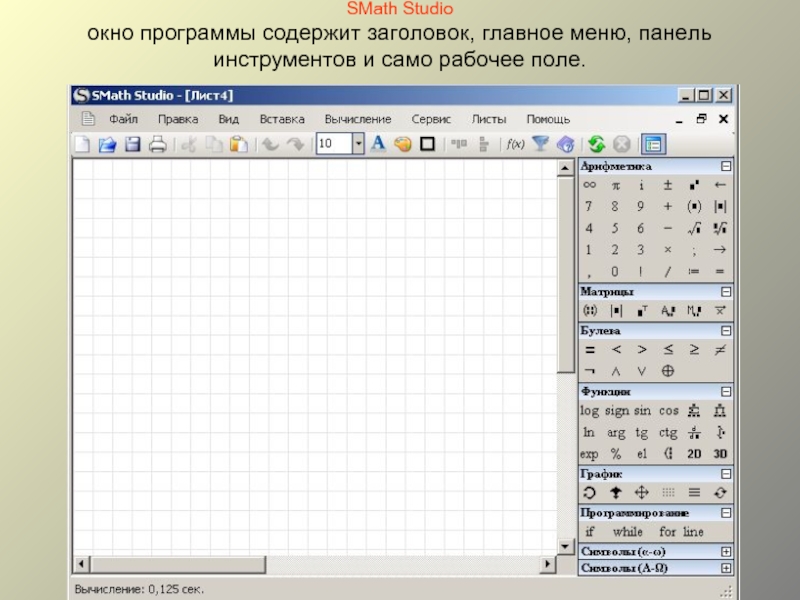
Слайд 4SMath Studio
Основное рабочее поле, в котором
и производятся все вычисления в форме, максимально
приближенной к нормальным математическим обозначениям.
Поле при стандартных настройках выглядит как тетрадный лист в клетку, и в нем, как на тетрадном листе, пользователь и вводит математические выражения.
Для этого надо просто установить курсор (красный крестик) в понравившееся место и начать ввод с клавиатуры. После того, как выражение введено, можно его посчитать, нажав «=». Похожим способом объявляется переменная: пишется имя, ставится знак присваивания «:=» с помощью кнопки на панели «Арифметика» или двоеточием на клавиатуре, вводится значение. Объявленную переменную можно использовать в выражениях, ее значение будет подставлено автоматически при вычислениях.
Источник: thepresentation.ru