Очень часто в работе учителя математики приходится работать с наглядным изображением геометрических фигур. Наиболее быстро, эффективно построить геометрическую фигуру можно, используя программу GeoGebra. Предлагаю мастер-класс «Построение чертежей в программе GeoGebra ».
Цель: обучить последовательному действию построения геометрической фигуры в программе GeoGebra на примере конкретной геометрической задачи.
Задач и:
— передать коллегам личный опыт по построению геометрических фигур в программе GeoGebra;
— показать удобство применения программы GeoGebra для построение геометрических фигур;
— научить строить геометрические фигуры в программе GeoGebra.
Рассмотрим построение чертежа на примере задачи из сборника для подготовки к ОГЭ в-6 №24 (ОГЭ. Математика. Типовые экзаменационные варианты. 36 вариантов / под ред. И. В. Ященко — Москва: издательство «Национальное образование»; 2021 г. — 224 с.):
В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
Как сделать уроки математики лучше? TeX, Beamer, GeoGebra
Сделаем первоначальные настройки программы. Уберем оси, нажав правой клавишей мыши и выделив пункт Оси

Таким образом, убрали оси

Далее настроим шрифт через настройки

Потом зададим обозначения только для точек

В программе GeoGebra на панели математических опций нажмите левой кнопкой мыши на символ треугольника.

Шаг 3
Вместо курсора-стрелки у вас появится курсор-крестик. Наведите курсор на полотно и нажмите левой кнопкой мыши один раз. Таким образом, вы зафиксируете первую вершину треугольника. Затем, переместив курсор в необходимое вам место полотна, нажмите левой кнопкой мыши снова один раз.
Произошла фиксация второй вершины треугольника и автоматически изобразилась первая сторона треугольника. Снова переместив курсор в другую часть полотна, нажмите левой кнопкой мыши третий раз. Произошла фиксация третей вершины треугольника с изображением второй стороны треугольника. И, наконец, совместите курсор с самым первоначальным положением (первой точкой/вершиной) для окончательного построения треугольника.

Построим высоту ВВ1, но сначала проведем прямую АС, для этого на панели математических опций нажмите левой кнопкой мыши на символ прямая

GeoGebra Classic App: When to Use?

и проводим высоту ВВ1 к прямой АС, для чего на панели математических опций нажмите левой кнопкой мыши на символ перпендикулярная прямая

и нажмите на точку В и на прямую АС, к которой проводим высоту

Нужно отметить точку В1, для этого на панели математических опций нажмите левой кнопкой мыши на символ точка

Выделяем на чертеже требуемую точку и получаем

Нам надо ее переименовать из D в В1. Это делается так: нажимаем правой кнопкой мыши на данную точку и выбираем пункт Переименовать

Вводим новое имя для точки (чтобы у точки задать нижний индекс, необходимо в имени индекс задать через нижнее подчеркивание _)

Получаем

Аналогично строим высоту СС1 и получаем чертеж

Отметим прямые углы, для этого на панели математических опций нажмите левой кнопкой мыши на символ угол

Далее выделаем последовательно точки А, В1, В

Но можно убрать надпись 90 градусов, для этого нажимаем правой кнопкой мыши и в окне выбираем Показывать обозначение


Аналогично обозначаем угол С1

Но по условию задачи нам нужен треугольник В1АС1, поэтому построим его аналогично шагу 2

Теперь можно внести изменения в чертеж, поменять место подписи букв и выделить треугольник штриховкой. Для этого щелкаем правой кнопкой мышки по треугольнику, появляется окно, где можно задать другие параметры


Скачать полученное изображение, выбрав опцию файл-экспорт-изображение

Теперь это изображение можно вставлять в ворд или в презентацию

Удачи вам во всех начинаниях!
Источник: xn--j1ahfl.xn--p1ai
Клавиши быстрого доступа в GeoGebra

Следующие tastaturgenveje и советы могут быть полезны, которые могли бы, При работе с GeoGebra.
Сочетания клавиш
Общий
- Нажмите ESC (Побег на клавиатуре) вернуться к кнопку переместить.
- Удерживая нажатой клавишу CTRL и теперь вы можете перетащить рисунок площадку с мышью (щелкните левой кнопкой мыши).
Файл
- CTRL + S – Сохраните файл
- CTRL + N – Создайте новый чертеж
- CTRL + O – Открыть файл
- CTRL + Р – Предварительный просмотр / печать
- ИТОГО + F4 – Близко
Редигер
- CTRL + В – Fortryd
- CTRL + И – Gentag (fortrydfortryd)
- CTRL + C – Kopier
- CTRL + В – Indsæt
- CTRL + И – Egenskaber
- CTRL + A – Vælg Alt
- CTRL + SHIFT + C – Kopier tegningen
Vis
- CTRL + SHIFT + A – Algebravindue
- CTRL + SHIFT + S – Regneark
- CTRL + SHIFT + К – CAS
- CTRL + SHIFT + 1 – Блокнот для рисования 1
- CTRL + SHIFT + 2 – Блокнот для рисования 2
- CTRL + SHIFT + L – Konstruktionsbeskrivelse
- CTRL + F – Genopfrisk
- CTRL + R – Genberegn Alle objekter
- CTRL + M – Масштаба для просмотра стандартных
- CTRL + + – Увеличить
- CTRL + – – Уменьшить
Matematiske – bogstaver О.Г. symboler
- ИТОГО + A – альфа α (Тощий OGSA SHIFT для Stort: A)
- ИТОГО + B – бета β (Тощий OGSA SHIFT для Stort: B)
- ИТОГО + Ре – дельта δ (Тощий OGSA SHIFT для Stort: Δ)
- ИТОГО + G – gamma γ (Тощий OGSA SHIFT для Stort: Γ)
- ИТОГО + L – лямбда λ (Тощий OGSA SHIFT для Stort: Λ)
- ИТОГО + M – м μ (Тощий OGSA SHIFT для Stort: Μ)
- ИТОГО + O – ° °
- ИТОГО + Р – PI π
- ИТОГО + И – Эйлер ℯ
- ИТОГО + F – Номера φ (Тощий OGSA SHIFT для Stort: Φ)
- ИТОГО + R – Kvadratrod
- ИТОГО + S – сигма σ (Тощий OGSA SHIFT для Stort: Σ)
- ИТОГО + Т – тета θ (Тощий OGSA SHIFT для Stort: Θ)
- ИТОГО + В – Омега ω (Тощий OGSA SHIFT для Stort: Ω)
- ИТОГО + 0 – Opløftet сезам 0. potens, Старый + 1 – Opløftet сезам 1. potens, Старый + 2 – Opløftet сезам 2. potens ОСВ.
Чаевые
Share this:
- Click to share on Twitter (Opens in new window)
- Click to share on Facebook (Opens in new window)
Источник: ggbkursus.dk
GeoGebra – самая популярная в мире математическая программа
GeoGebra — самая популярная в мире бесплатная математическая программа. С помощью обучающей программы по математике, можно будет выполнить множество полезных вещей: анализировать функции, строить графики, решать задачи, работать с функциями и т. д. Интерфейс программы GeoGebra (ГеоГебра) напоминает классную доску, на которой можно рисовать графики, создавать геометрические фигуры и т. п. В окне программы будет наглядно отображены производимые изменения: если вы измените уравнение, кривая перестроится, изменится масштаб или ее положение в пространстве, уравнение, написанное рядом с кривой, автоматически будет скорректировано, согласно новым значениям.
Программу GeoGebra широко используют в мире миллионы пользователей для обучения алгебре и геометрии. Процесс обучения нагляден благодаря визуальной форме использования приложения. Возможности программы по математике не ограничиваются только построением графиков, программу GeoGebra можно будет использовать для интерактивных чертежей при решении геометрических задач.
Программа ГеоГебра обладает мощными и функциональными возможностями, которые позволяет наглядно и просто обучаться математике. Приложение включает в себя геометрию, алгебру, есть возможность совершать арифметические операции, создавать таблицы, графики, возможна работа со статистикой, работа с функциями, поддерживается создание анимации и т. д. В программе GeoGebra можно будет создавать различные 2D и 3D фигуры, интерактивные ролики, которые затем можно будет размещать в интернете.
Все приложения, входящие в состав программы GeoGebra, доступны и синхронизируются между собой для работы в составе одного пакета. GeoGebra была создана Маркусом Хохенвартером. Программа написана на языке Java, приложение поддерживает работу в различных операционных системах: Windows, Mac OS X, Linux, Android. С сайта производителя можно будет скачать обычную версию программы GeoGebra для установки на компьютер. Также можно будет скачать переносную версию программы (GeoGebra Portable) для соответствующей операционной системы. geogebra скачать После запуска GeoGebra на компьютере, ознакомимся с интерфейсом программы.
Интерфейс GeoGebra
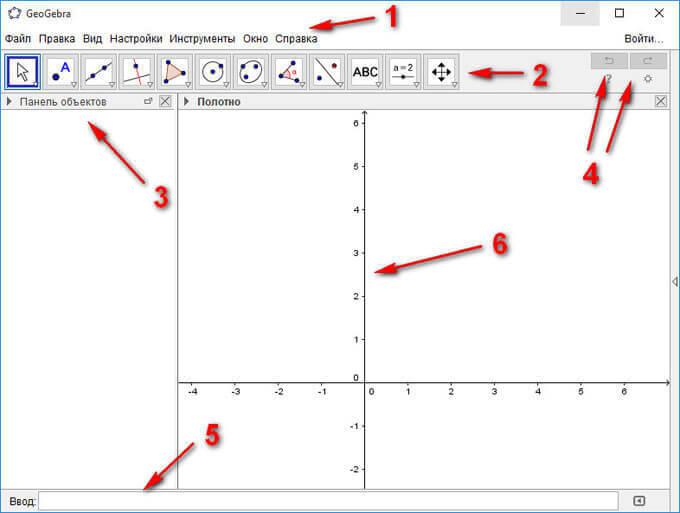
Интерфейс программы GeoGebra напоминает графический редактор. Программу можно использовать для черчения, но это не основное предназначение приложения.
Давайте рассмотрим основные элементы интерфейса программы GeoGebra:
- Полоса меню. Из меню вы можете изменить настройки программы.
- Панель инструментов. Здесь находятся инструменты для создания объектов. После щелчка по треугольнику в правом нижнем углу кнопки, будут открыты дополнительные инструменты. Операции, доступные в панели инструментов, можно производить с помощью строки ввода.
- Панель объектов. В Панели объектов отображаются введенные переменные и функции. Вместо имен переменных здесь отображаются их значения. Для того, чтобы увидеть формулу в символьном виде, нужно будет кликнуть по ней правой кнопкой мыши.
- Кнопки «Отменить» и «Повторить».
- Строка ввода. Это основной инструмент при работе в программе GeoGebra. Здесь вводятся команды и формулы, задаются значения переменных. Справа от строки ввода расположена кнопка «Список команд». С помощью дополнительных команд можно будет вводить команды и отсутствующие на клавиатуре символы.
- Рабочая область. Все построения в программе производятся в рабочей области. Вы можете изменить масштаб с помощью колесика мыши, перемещать по рабочей области ось координат.
Далее попытаемся выполнить некоторые элементарные действия в программе GeoGebra.
Построение графика функции в GeoGebra
Для построения графика функции достаточно будет набрать ее в поле ввода. Для отображения параболы нужно будет написать в строке «Ввод» следующее выражение:
Символ «^» в программе GeoGebra обозначает возведение в степень.
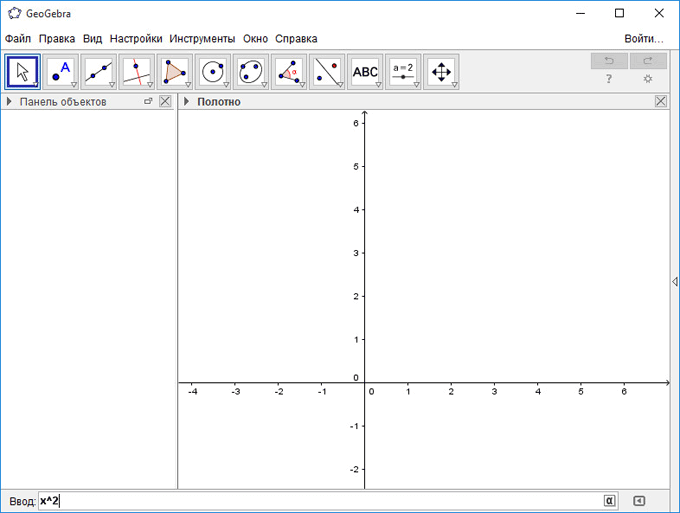
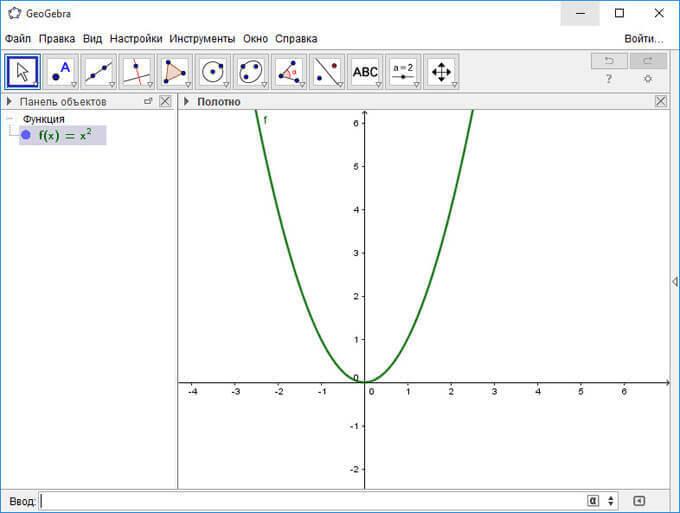
Далее нажмите на кнопку «Enter». После этого в рабочей области будет построен график. Рисунок можно будет масштабировать с помощью колесика мыши. Для перемещения рабочей области нужно будет нажать на клавишу «Shift», одновременно удерживая нажатой левую кнопку мыши.
Вы можете перемещать сам график при помощи нажатой правой кнопки мыши, при этом, в Панели объектов будут отображены изменения в уравнении.
Вы можете добавить в уравнение переменные параметры, например, следующие (введите их строку ввода поочередно):
a=1
b=1
(x+a)^2+b
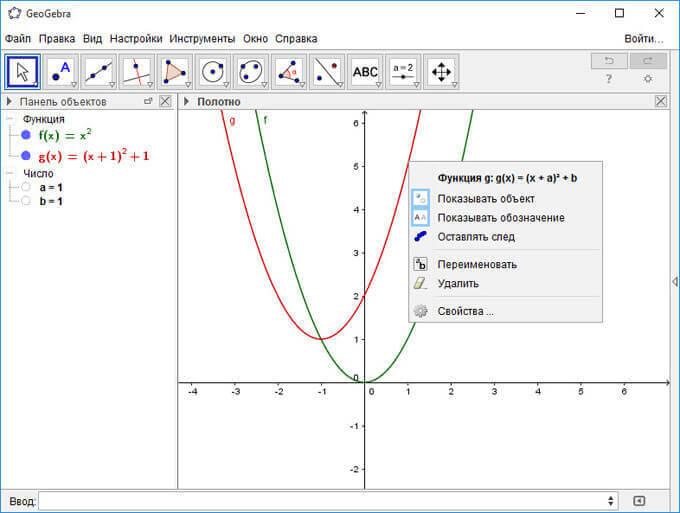
В рабочей области появится еще одна парабола, смещенная влево на одну единицу. Кликнув по графику, вы можете из открывшегося контекстного меню производить необходимые действия.
Создание треугольника в GeoGebra
Давайте попробуем начертить треугольник в программе GeoGebra. Для этого нужно будет перейти в «геометрический» режим для того, чтобы включить отображение сетки, и отключить отображение оси координат.
Кликните правой кнопкой мыши по оси координат, в контекстном меню выберите пункт «Сетка», а затем там кликните по пункту «Оси» для отключения оси координат. На панели инструментов нажмите на кнопку «Многоугольник».
После этого нарисуйте треугольник, последовательно установив три вершины. При необходимости, вы можете ввести точные координаты. Для этого вам нужно будет кликнуть по точке правой кнопкой мыши.
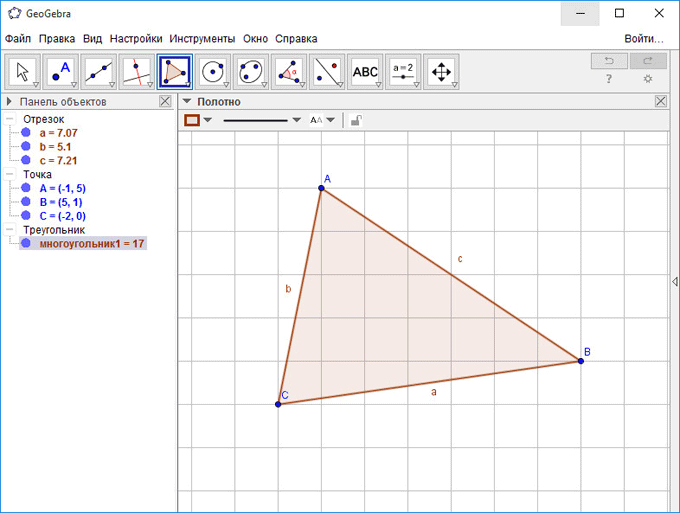
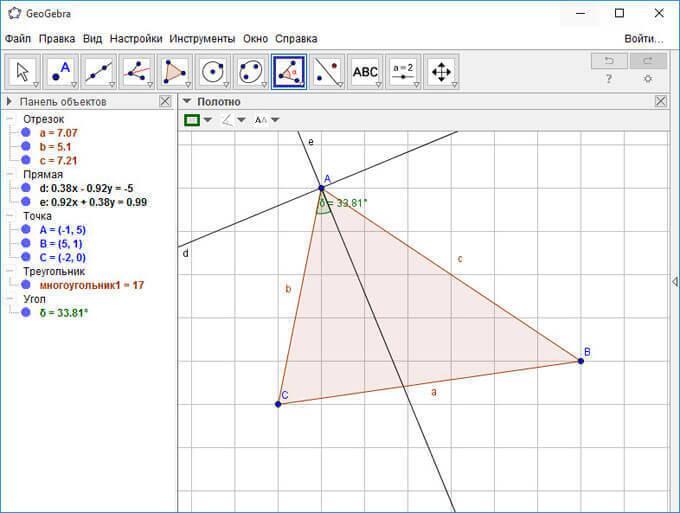
Далее вы можете создать биссектрису угла. Для этого нажмите на треугольную кнопку под кнопкой «Перпендикулярная прямая», а затем выберите из выпадающего списка инструмент «Биссектриса угла». После этого, кликните по двум отрезкам образующих угол, биссектриса будет создана.
Вы можете обозначить угол. Для этого нажмите на кнопку инструмента «Угол» в Панели инструментов. Для отображения интересующего вас угла выберите три точки или две прямые.
Geogebra online
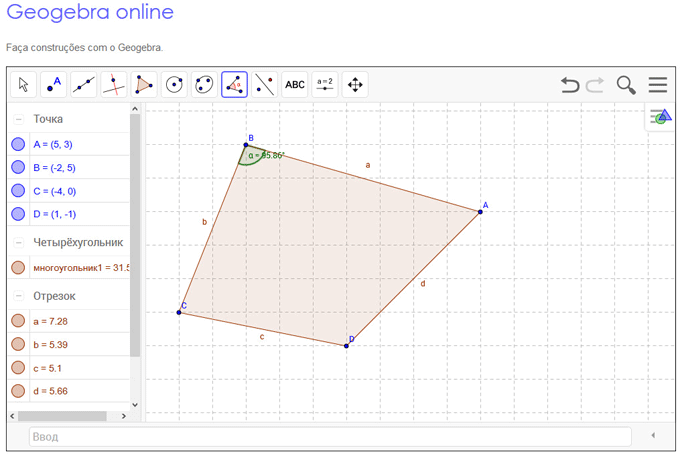
У программы GeoGebra имеется онлайн версия: Geogebra online (ГеоГебра онлайн). После перехода на сайт www.geogebra.org , вы можете открыть программу GeoGebra в своем браузере для выполнения необходимых действий. Таким образом, даже не устанавливая программу GeoGebra на свой компьютер, при наличии интернета, вы можете работать в этой математической программе, войдя на онлайн сервис со своего мобильного устройства.
Расширение GeoGebra
Создано расширение GeoGebra для браузера Google Chrome. Обратите внимание на количество пользователей расширения: более 2.6 миллиона человек. Немногие расширения из магазина Chrome могут сравниться с такими цифрами. Это свидетельствует о том, что приложение GeoGebra широко используется в мире для образовательных целей.
Для входа в расширение кликните по кнопке «Сервисы» на панели закладок в браузере Google Chrome. После этого будет открыто окно расширения GeoGebra в вашем браузере. На начальном экране вы можете выбрать раздел математики, с которым далее вы будете работать в приложении.
Дополнительные материалы по работе в программе, вы можете найти на сайте производителя приложения, и в интернете.
Заключение
Бесплатная программа GeoGebra предназначена для обучения математике. С помощью программы GeoGebra (ГеоГебра) можно обучаться или работать в динамической математической среде, включающей в себя геометрию, алгебру, другие разделы, с широкими функциональными возможностями.
Программы для запуска, обновления и оптимизации работы компьютера.
Источник: www.liveinternet.ru