Чернушко, М. М. Применение машины Тьюринга для реализации алгоритмов шифрования / М. М. Чернушко. — Текст : непосредственный // Технические науки: теория и практика : материалы II Междунар. науч. конф. (г. Чита, январь 2014 г.). — Т. 0. — Чита : Издательство Молодой ученый, 2014. — С. 19-22. — URL: https://moluch.ru/conf/tech/archive/88/4317/ (дата обращения: 12.07.2023).
В 1936 году английским математиком Аланом Мэтисоном Тьюрингом (1912–1954) была представлена абстрактная вычислительная машина, впоследствии названная «Машиной Тьюринга», которую можно считать моделью компьютера общего назначения. Она позволила формализовать понятие алгоритма и до сих пор используется во множестве теоретических и практических исследований.
В рамках данной статьи будет рассмотрена реализация при помощи машины Тьюринга алгоритма симметричного шифрования методом перестановки и алгоритма шифрования методом одноалфавитной подстановки.
Машина Тьюринга (МТ) состоит из двух частей — ленты и автомата. Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые никак не нумеруются и не именуются. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться — в неё можно записать другой символ или стереть находящийся в ней символ.
Как запрограммировать на машине Тьюринга вычитание? Душкин объяснит
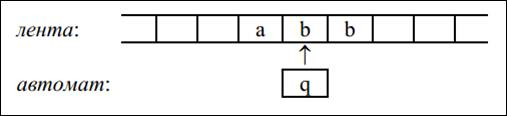
Рис. 1. Лента и автомат
Для реализации примеров, описанных в статье, используется имитатор детерминированной машины Тьюринга (далее ИМТ), расположенный в сети Интернет по адресу «http://matinf.vsgao.com/simulator/tm.html», исходя из этого, в дальнейшем, для удобства будут использоваться обозначения, принятые в этом ИМТ.
Договоримся пустое содержимое клетки называть символом «пусто» и обозначать знаком «B». Данное соглашение удобно тем, что операцию стирания символа в некоторой клетке можно рассматривать как запись в эту клетку символа «В».
Автомат — это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ — видимый символ; содержимое соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний, которые будем обозначать буквой «q» с номерами: «q1», «q2» и т. п. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы «b» на «a»), находясь в другом состоянии — другую операцию.
Автомат может выполнять три элементарных действия:
а) записывать в видимую клетку новый символ (менять содержимое других клеток автомат не может);
б) сдвигаться на одну клетку влево или вправо («перепрыгивать» сразу через несколько клеток автомат не может);
в) переходить в новое состояние.
Ничего другого делать автомат не умеет, поэтому все более сложные операции так или иначе должны быть сведены к этим трём элементарным действиям. [1]
Машина Тьюринга. Введение. Понятие машины тьюринга. Решение задачи
МТ работает тактами, которые выполняются один за другим. На каждом такте автомат МТ выполняет три следующих действия, причем обязательно в указанном порядке:
а) записывает некоторый символ «S» в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется);
б) сдвигается на одну клетку влево (обозначение — L), либо на одну клетку вправо (обозначение — R), либо остается неподвижным (обозначение — H).
в) переходит в некоторое состояние «q» (в частности, может остаться в прежнем состоянии).
Формально действия одного такта будем записывать в виде тройки: «S [L,R,H]q», где конструкция с квадратными скобками означает возможность записи в этом месте любой из букв «L», «R» или «H». Например, такт «*Lq8» означает запись символа «*» в видимую клетку, сдвиг на одну клетку влево и переход в состояние «q8». [1]
Сама по себе МТ ничего не делает. Для того, чтобы заставить её работать, надо написать для неё программу. Для удобства эта программа записывается в виде следующей таблицы:
Пример программы для МТ в табличной форме
Слева перечисляются все состояния, в которых может находиться автомат, сверху — все символы (в том числе и «B»), которые автомат может видеть на ленте (какие именно символы и состояния указывать в таблице — определяет автор программы). На пересечениях же (в ячейках таблицы) указываются те такты, которые должен выполнить автомат, когда он находится в соответствующем состоянии и видит на ленте соответствующий символ.
В целом таблица определяет действия МТ при всех возможных сочетаниях входных символов и состояний автомата и тем самым полностью задаёт поведение МТ. Описать алгоритм в виде МТ — значит предъявить такую таблицу. [1] Однако, в используемом в данной статье ИМТ, программа вводится построчно, где каждая строка представляет собой такт, выполняемый в зависимости от текущего состояния автомата и входящего символа. Например, запись «1q3->2q4L» можно истолковать так: если входящий символ «1» и текущее состояние «q3», то записать в текущую клетку символ «2», перейти в состояние «q3» и сдвинуть автомат влево. При этом последовательность записи роли не играет.
До выполнения программы нужно проделать следующие предварительные действия. Во-первых, надо записать на ленту входное слово, к которому будет применена программа (в используемом ИМТ оно называется «конфигурация»). Входное слово — это конечная последовательность символов, записанных в соседних клетках ленты; внутри входного слова пустых клеток быть не должно, а слева и справа от него должны быть только пустые клетки. Во-вторых, надо установить автомат в состояние «q1» (указанное в таблице первым) и разместить его под первым символом входного слова.
После этих предварительных действий начинается выполнение программы. В таблице отыскивается ячейка на пересечении первой строки (т. к. автомат изначально находится в состоянии «q1») и того столбца, который соответствует первому символу входного слова (это необязательно левый столбец таблицы), и выполняется такт, указанный в этой ячейке. В результате автомат окажется в новой ячейке, соответствующей новому входящему символу и состоянию автомата и выполняется такт из этой ячейки. [1]
В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние «q0» (в используемом в данной работе ИМТ состояние «q0» обозначается как «STOP»). Эти клетки называются клетками останова. Дойдя до любой такой клетки, МТ прекращает свою работу. [5]
15. Машина Тьюринга. Проблема остановки. Вычислимость.
Машина Тьюринга — это головка для считывания/записи по бесконечной ленте.
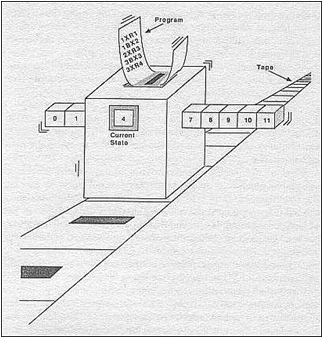
Для ее работы необходимо задать 2 алфавита: символов A= и состояний машины Q=, причем q 0 принимается за пассивное состояние, q 1 за начальное, а a 0 -это пустая ячейка.
Машина видит только одну ячейку и в соответствии с алгоритмом записывает новую букву в ячейку, выполняет сдвиг или остается недвижимой, переходит в новое состояние.
Программу для м. Т. можно представить в виде матрицы:
т.е. сначала мы записываем действие с ячейкой (написать что-то, не трогать ничего), потом передвижение по ленте, а потом состояние, в которое машина перейдет.
Если в машине Тьюринга T, которая кодируется, δ(i, a) = ( j, b, D), то подблок, соответствующий состоянию i и входному символу a, будет содержать j единиц, за которыми следует символ D ∈ , а за ним b ∈ . Если δ(i, a) не определено, то соответствующий подблок будет содержать единственный нуль.
Так же надо выделить состояния, при которых машина остановится: терминальные (допускающие) состояния. Иначе она будет вечно бегать по бесконечной ленте.
Машина Тьюринга не решает проблему остановки.
Даны описание алгоритма и его начальные входные данные, требуется определить, сможет ли выполнение алгоритма с этими данными завершиться когда-либо. Альтернативой этому является то, что он работает всё время без остановки.
Назовем Анализатором гипотетический алгоритм, который получает на вход пару натуральных чисел(N,X), и
§ останавливается и возвращает 1, если другой алгоритм с номером N не останавливается, получив на вход X
§ не останавливается в противном случае (если другой алгоритм с номером N останавливается, получив на вход X).
Если применить алгоритм к самому себе, то он не сможет работать, потому что должен будет остановиться тогда, когда он сам не останавливается, и не останавливаться в том случае, если он сам остановится.
Более сложное доказательство здесь Проблема вычислимости заключается в том, что есть такие «алгоритмы», результат действия которых мы не можем вычислить. Примером такого «алгоритма» является бесконечная снежинка Коха:

1. Мы рисуем треугольник
2. На следующем шаге на каждой его стороне мы рисуем еще по треугольнику
3. На следующем — на каждом из полученных треугольников еще по треугольнику
4. И так на каждом последующем шаге мы рисуем по треугольнику на каждом из треугольников, полученных на предыдущем шаге (вот так, как это показано на картинке)
Проблема: если мы поставим рядом с такой снежинкой точку, то мы не можем определить, попадет ли эта точка в снежинку, когда та будет разрастаться, на определенном шаге реализации этого алгоритма. Если точка не попадет в снежинку на 55-ом шаге, мы не знаем, случится ли это на 70-ом или на 125-ом шаге — алгоритм бесконечен.
Источник: psyphy.fandom.com
Лаба №1. Машины Тьюринга
![]()
ais_Laba_1.rar
Целью данного занятия является закрепление знаний по построению и работе машин Тьюринга, которые являются математическими (формальными) моделями алгоритмов.
Задание 1. Построить таблицу машины Тьюринга, которая заменяет все единицы на нули, а все нули на единицы. Пример. Исходное число 111001. Результат – 000110.
Задание 2. Построить таблицу машины Тьюринга, которая удаляет из числа все нули, например, число 1001110 преобразует к виду 1111. Эта задача уже сложнее и требует ввести в рассмотрение более двух состояний.
Задание 3. Построить машину, имеющую два конечных состояния, условно обозначаемых как YES и NO. Машина должна завершить работу в состоянии YES, если число единиц в записи числа нечетное, и в состоянии NO – в противном случае.
Задание 4. Построить машину, имеющую два конечных состояния, условно обозначаемых как YES и NO. Машина должна завершить работу в состоянии YES, если в записи числа имеется три подряд идущих единицы, и в состоянии NO – в противном случае.
Задание 5. Построить машину Тьюринга, которая получает обратный порядок записи числа, например, исходное число 111001, результат 100111.
Задание 6. Построить машину Тьюринга, которая меняет местами соседние два элемента попарно. Пример. Исходное число 011001 заменяется на 100110.
Общий вопрос. Оценить, как изменяется число тактов (по какому закону), совершаемых машиной при линейном увеличении размерности входного слова. В качестве примера взять Задание 1 и Задание 2. (Следует показать, что время работы также возрастает линейно).
[остальное в файле ниже]
Файл с заданием:
![]()
внутри doc
Источник: bsuir-helper.ru