Как задать программу в excel

Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле

Построение графика линейной функции в Excel

Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].

Подготовка расчетной таблицы

В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.

Как изменить маленькие буквы в excel на заглавные без формул

Далее строим таблицу значений линейной функции:

• В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
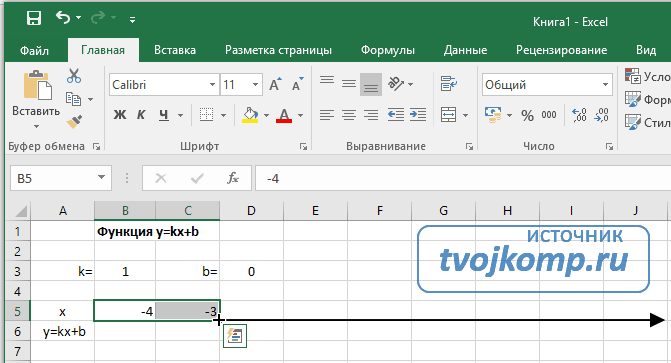
• Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
• Выделяем эти ячейки.
• Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.

Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3

Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.

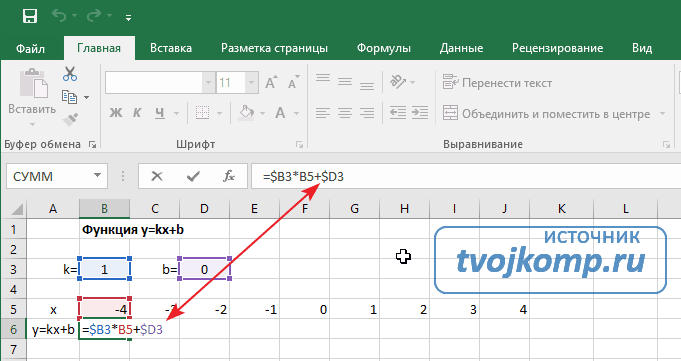
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.

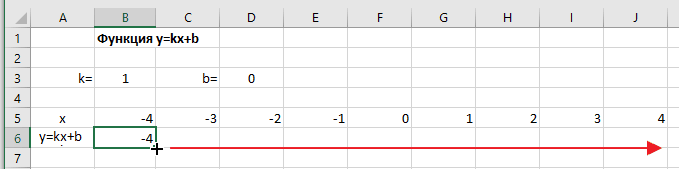
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.

Построение графика функции

Выделяем прямоугольный диапазон ячеек A5:J6.

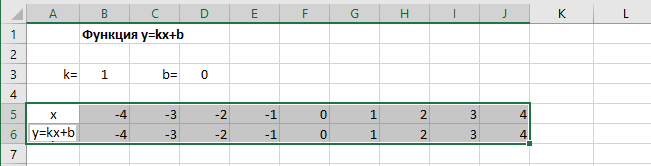
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.

Лайфхак с функцией повтор в excel

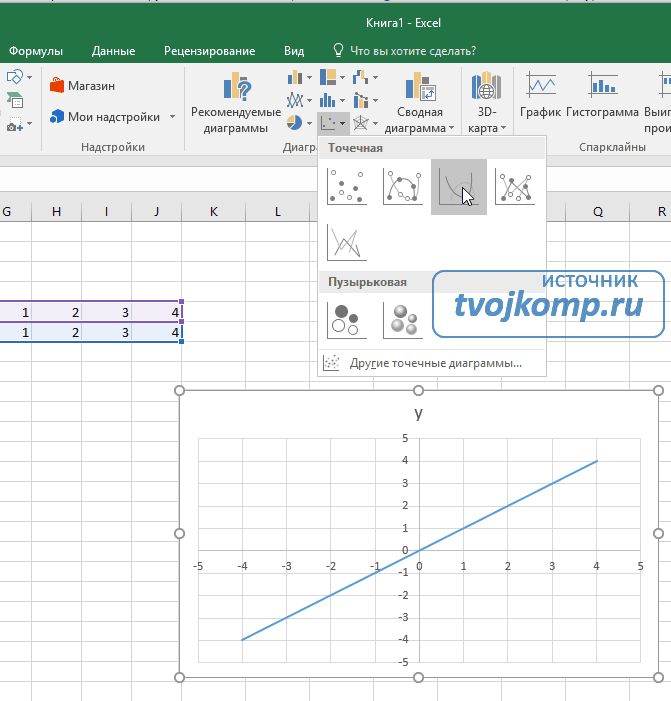
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.

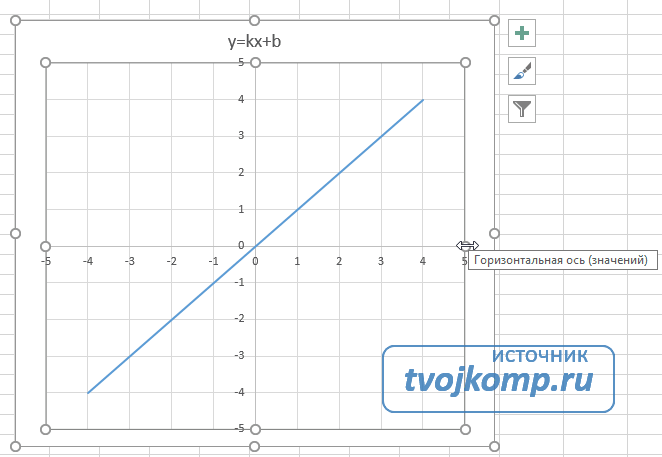
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..

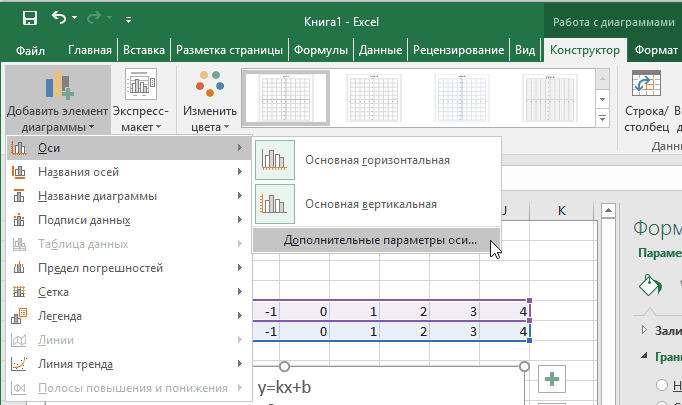
В правой части окна появиться боковая панель настроек Формат оси.

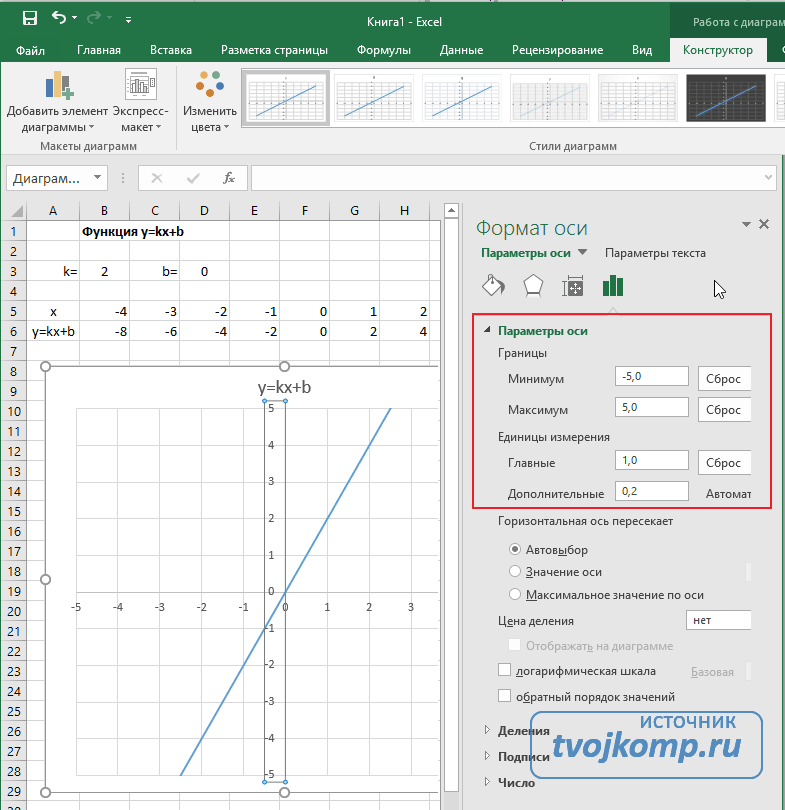
• Кликните на раскрывающийся список Параметры оси.
• Выберите Вертикальная ось (значений).
• Кликните зеленый значок диаграммы.
• Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
• Повторите тоже для горизонтальной оси.

Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.

Построение графиков других функций

Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.

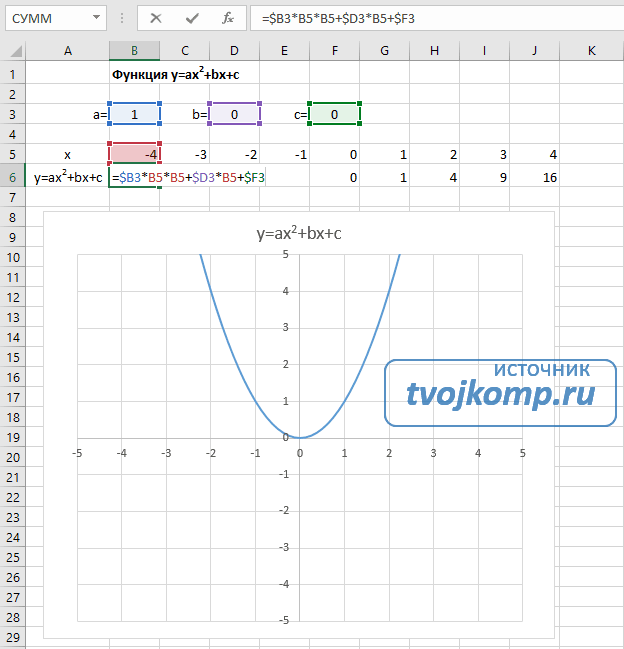
Квадратичная функция y=ax 2 +bx+c

Выполните следующие действия:

• В первой строке меняем заголовок
• В третьей строке указываем коэффициенты и их значения
• В ячейку A6 записываем обозначение функции
• В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
• Копируем её на весь диапазон значений аргумента вправо

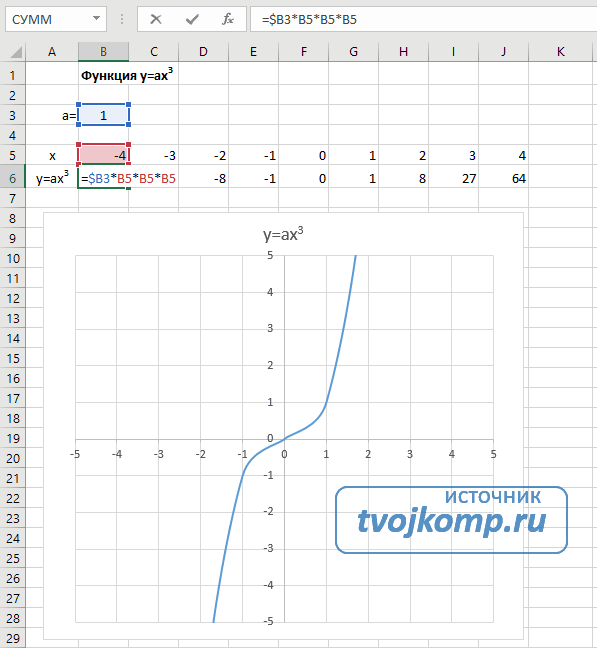
Кубическая парабола y=ax 3

Для построения выполните следующие действия:

• В первой строке меняем заголовок
• В третьей строке указываем коэффициенты и их значения
• В ячейку A6 записываем обозначение функции
• В ячейку B6 вписываем формулу =$B3*B5*B5*B5
• Копируем её на весь диапазон значений аргумента вправо

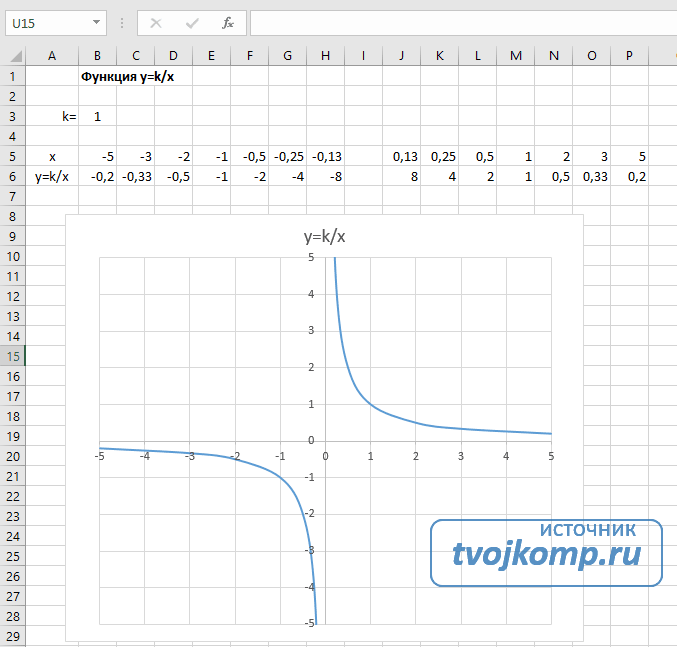
Гипербола y=k/x

Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.

Далее выполните действия:

• В первой строке меняем заголовок.
• В третьей строке указываем коэффициенты и их значения.
• В ячейку A6 записываем обозначение функции.
• В ячейку B6 вписываем формулу =$B3/B5
• Копируем её на весь диапазон значений аргумента вправо.
• Удаляем формулу из ячейки I6.

Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.

• Кликните диаграмму
• На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
• Откроется окно мастера ввода данных
• Выделите мышкой прямоугольный диапазон ячеек A5:P6
• Нажмите ОК в окне мастера.

Построение тригонометрических функций sin(x) и cos(x)

Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже

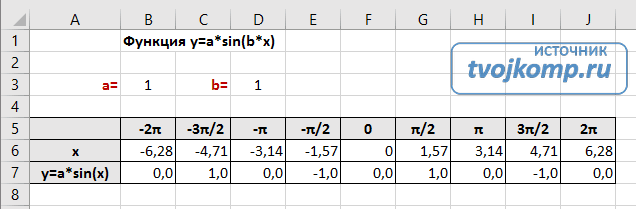
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.

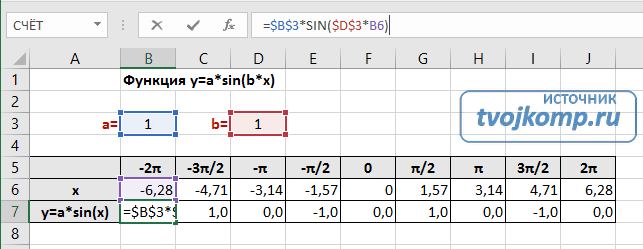
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.

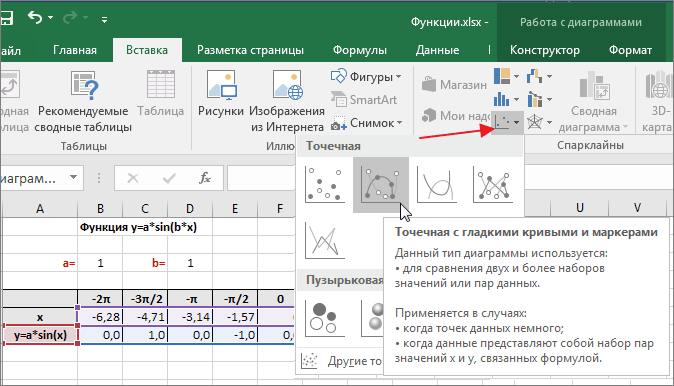
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.

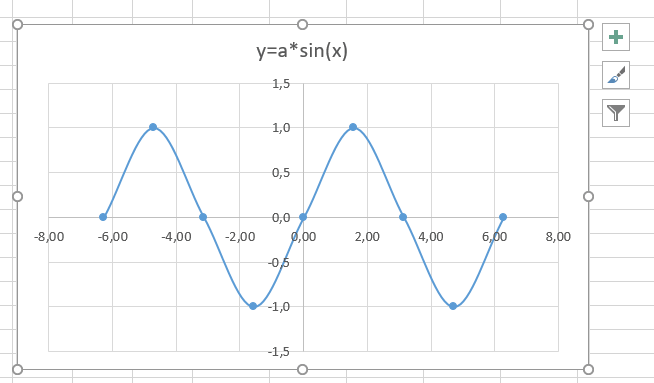
В итоге получим диаграмму.

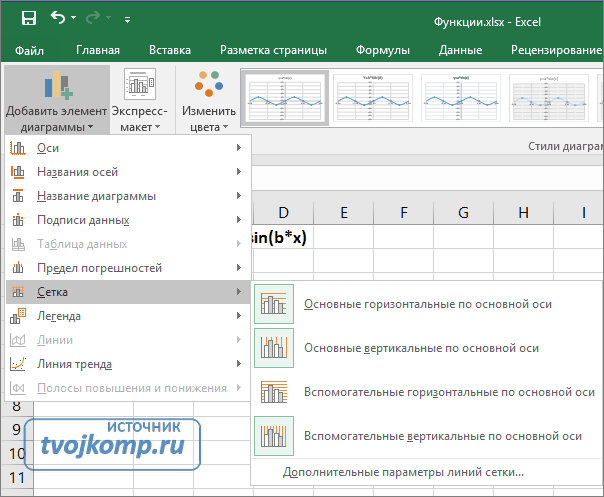
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.

Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.

Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.

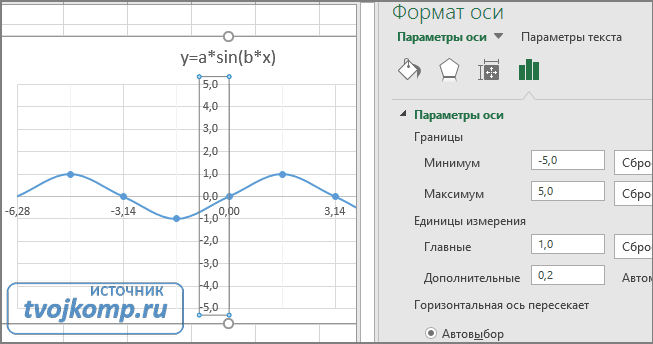
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.

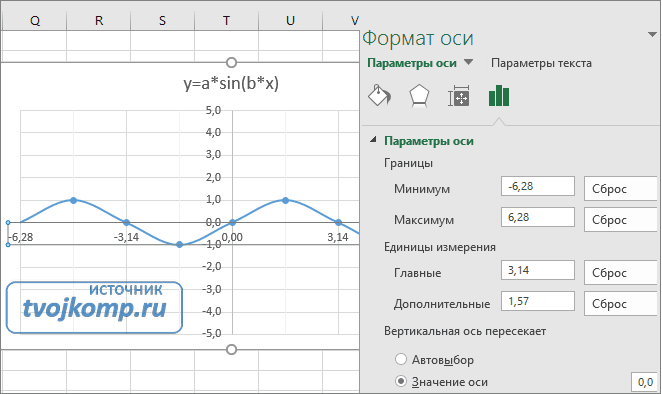
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.

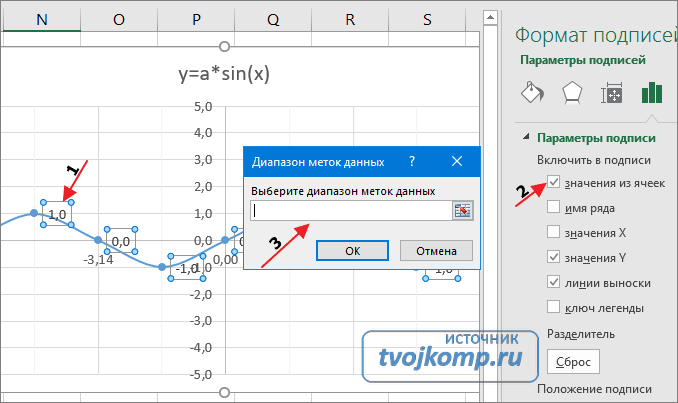
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.

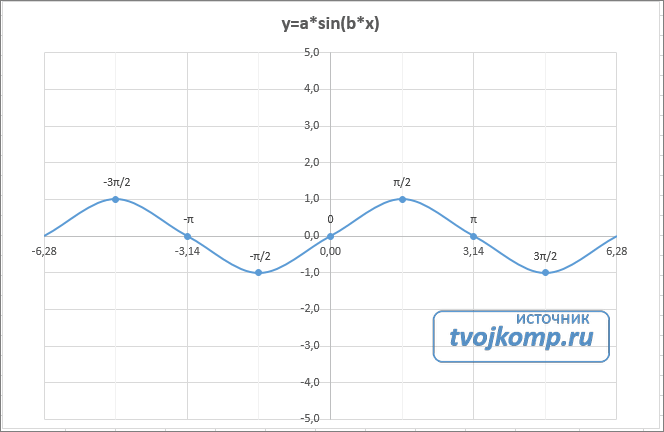
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).

Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.

Дополнительные статьи по теме:

• Знакомство с таблицами в Excel
• Изменение строк и столбцов в Excel
• Работа с ячейками: объединение, изменение, защита…
• Ошибки в формулах: почему excel не считает
• Использования условий в формулах Excel
• Функция CЧЕТЕСЛИМН
• Работа с текстовыми функциями Excel
• Все уроки по Microsoft Excel

ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

2 53 469 views
Вам также может быть интересно

Microsoft Excel 0 3 549 views

Счетеслимн excel примеры Рассмотрим функции: СЧЁТЕСЛИ(диапазон;критерий) и СЧЁТЕСЛИМН(диапазон_условия; условие; . ). Функция счетесли подсчитывает количество непустых

Microsoft Excel 4 20 176 views

Здравствуйте, друзья! Часто ли вам приходится делать выбор? Например, захотели купить новый телефон, а

Источник: tvojkomp.ru

Создание макросов в excel (на примере)

Создание макросов в excel — это задача, которая требует определенного уровня знаний и навыков. Но один раз разобравшись с их написанием, можно очень сильно облегчить себе работу. Так как использование макросов позволяет автоматизировать монотонные операции и передать excel всю работу по выполнению одних и тех же действий.
В статье рассмотрены основы создания макросов, благодаря которым вы напишите свой первый макрос и поймете, захотите ли дальше изучать данную тему.

Вкладка «Разработчик»

Для начала нужно в экселе отобразить вкладку «Разработчик»:

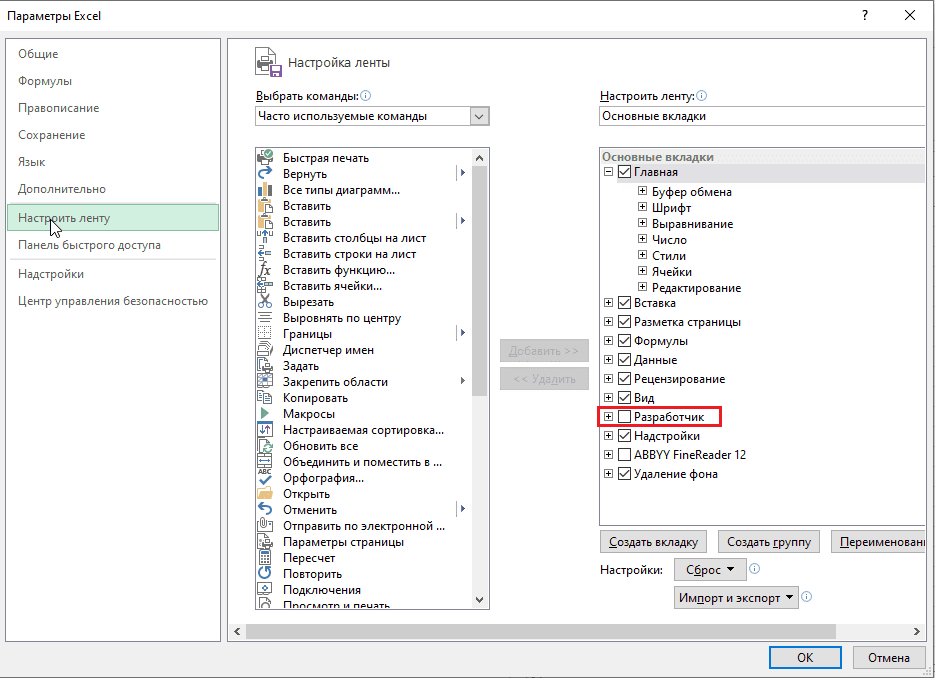
• Выполнить команды: Файл ➜ Параметры ➜ Настроить ленту ➜ вкладка «Настроить ленту».
• Справа на панели установить флажок «Разработчик» ➜ Нажать «ОК».

Переход в окно макросов

• Перейти на вкладку «Разработчик» -> В группе «Код» нажать кнопку «Visual Basic».

Интерфейс окна макросов Excel

Окно кода макросов

Чтобы разобраться, как работает макрос, рассмотрим код.

Cells(4, 2) = «Расчет значений» ‘ текст в ячейке
Cells(6, 5) = 5 ‘ число в ячейке
Cells(8, 3) = Cells(6, 3) * Cells(7, 3) ‘ формула в ячейке

Cells(4, 2).Font.Size = 14 ‘ размер шрифта
Cells(4, 2).Font.Bold = True ‘ жирный
Cells(4, 2).Font.Italic = True ‘ курсив
Cells(4, 2).Font.Underline = xlUnderlineStyleSingle ‘ подчеркивание
Cells(4, 2).Interior.Color = 65535 ‘заливка ячейки

Пример макроса с внесением значений разного типа, а также форматированием ячеек с комментариями можно скачать по ссылке.

Начало создания макроса

• Любой макрос должен начинаться с оператора Sub, за которым идет имя макроса и список аргументов (если аргументов нет, то скобки надо оставить пустыми).
• Любой макрос должен заканчиваться оператором End Sub.
• Все, что находится между Sub и End Sub — тело макроса, т.е. команды, которые будут выполняться при запуске макроса.
• Комментарий пишется после знака апострофа. Он нужен для того, чтобы делать пометки для себя, так как открыв макрос через n-ное количество времени можно не вспомнить о чем он. Также они могут понадобится при написании другого макроса в качестве шпаргалки по командам.

Ячейки в макросе

• Ячейка в макросе обозначается Cells(4, 1), где 4-номер строки, 1-номер столбца
• Каждой ячейке можно присвоить разные значения, например:

• Cells(4, 1) = «Расчет значений» ➤ текст (пишется в кавычках)
• Cells(4, 1) = 5 ➤ значение
• Cells(4, 1) = Cells(2, 1) + Cells(3, 1) ➤ сумма других ячеек
• Cells(4, 1) = Cells(2, 1) * 20 + Cells(3, 1) * 80 ➤ значение, полученное при вычислении формулы

Формат ячеек

• Задать формат ячейке можно задать через свойства ячейки. В нашем примере это размер шрифта, формат шрифта и заливка ячейки.
• В файле примера макроса рассмотрены заливка ячеек, границы ячеек и диапазона ячеек для всей таблицы, отдельных границ с применением разной толщины границ (скачать по ссылке).
• Другие команды для форматирования ячеек можно найти в интернете.

Кнопка для запуска макроса

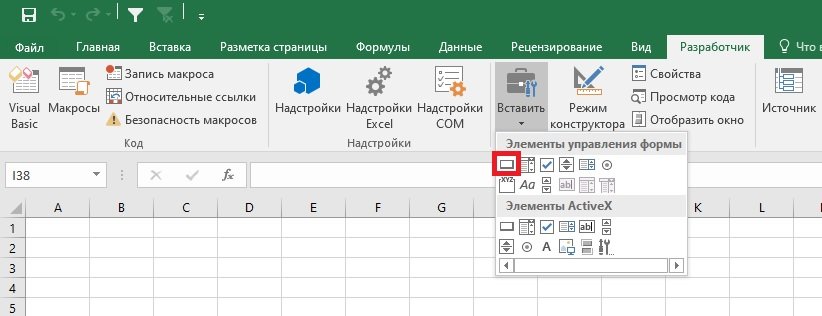
• Вкладка Разработчик ➜ группа Элементы управления ➜ кнопка Вставить
• В группе Элементы управления формы нажать «Кнопка» (изображение кнопки) .
• Щелкнуть на листе место, где должен быть расположен левый верхний угол кнопки. Появится всплывающее окно Назначение макроса.
  Назначьте кнопке макрос и нажмите кнопку ОК.
• Чтобы задать свойства кнопки, щелкните ее правой кнопкой мыши и выберите форматирование.

Если Вы хотите начать изучать макросы excel, то переходите к курсу «Excel макросы: генератор простых примеров по математике«. Настройку работы макросов excel и их создание лучше осваивать на конкретном примере, где понятна цель написания программы.

Перейти к урокам по изучению макросов в Excel на примере формирования примеров по математике случайным образом. Курс состоит из 10 уроков + шаблоны готовых макросов.

Источник: intmag24.ru

Начала программирования в Excel

Оптимизационные задачи, конечно же, не относятся к числу задач первоначального обучения программистов. Однако, это важный класс задач при обучении математиков. Кроме того, роль играет и традиция, восходящая еще к тому периоду, когда вычислительная математика определяла развитие программирования. Нужно сказать, что в Excel встроены мощные средства, позволяющие решать задачи этого класса. Следуя воспитанию и традиции, я уделю этим задачам достаточно много внимания в последующих главах.

Хранение данных

Одним из недостатков традиционных подходов, при которых обучение тесно связывается с изучением некоторого языка программирования, является то, что базы данных, не являющиеся частью языка программирования, появляются где-то на поздних этапах. В Excel эта трудность преодолевается естественным путем.

Благодаря инкапсуляции, о которой я говорил выше, рабочая книга представляет собой своеобразную базу данных. К этому следует добавить, что в Excel есть и специальные средства — списки Excel, — позволяющие выполнять специальные операции над данными: фильтрацию, поиск и другие типичные операции над данными. Нельзя не упомянуть, одно из главных назначений Excel состоит в том, чтобы служить средством анализа и отображения данных, поступающих от различных внешних источников данных — баз данных, хранилищ как структурированной, так и неструктурированной информации. Так что средств, позволяющих работать с собственными и внешними базами данных в Excel предостаточно.

Программирование на VBA

Excel дает возможность решать многие задачи, не требуя привлечения языка программирования, прежде всего, благодаря свойствам машины вычислений. Понятно, что такая возможность и делает Excel столь привлекательным для многочисленных пользователей.

Но работа с машиной вычислений Excel полезна и при обучении программистов, тем более что процесс вычислений не является скрытым — все формулы видны, все значения доступны. Более того, различные графики могут помочь проследить за деталями процесса вычислений. Но, конечно, для программистов главное достоинство состоит в том, что они могут сочетать работу руками с программированием на языке VBA. Языку VBA я посвятил отдельную книгу [1], где достаточно много было сказано о тех его свойствах, которые делают этот язык привлекательным для целей начального обучения программированию. Он вполне подходит на роль «первого языка», с которого следует начинать осваивать программирование и который оказывает большое влияние на последующий стиль программирования.

По существу, MacroRecorder — это обычный транслятор «необычного» языка действий. Включив запись макроса, Вы инициируете запись всех Ваших действий: выбор той или иной ячейки или области, запись в ячейку значения или формулы, вызов некоторой функции, построение диаграммы или таблицы и т.д. В любой момент Вы можете выключить запись действий.

В результате MacroRecorder создаст макрос на языке VBA, запуск которого приведет к тому же эффекту, что и Ваши действия. Таким образом, один раз, сделав все руками, создав документ или его фрагмент, Вы бесплатно получаете программу, которая делает то же самое. Вся штука в том, что программу можно запускать многократно.

Что же касается действий пользователя, возможно, весьма квалифицированно работающего в среде Office, то я уже не раз говорил, что они естественным образом интерпретируются, как действия над объектами того или иного приложения Office — вызов и изменение соответствующих свойств и методов этих объектов. Для программных сред, в которых пользователю предоставляются широкие возможности манипуляции над объектами, видимыми на экране, другими словами, для сред визуального программирования инструментарий, подобный MacroRecorder, совершенно естественная вещь, — все равно за действиями пользователя нужно следить и выполнять их. Транслируя действия пользователя, MacroRecorder создает макрос — процедуру без параметров на языке VBA. Созданный макрос можно выполнить в любой нужный момент. Более того, можно создать инструментальную кнопку и связать с ней созданный макрос, — теперь щелчок пользователя по кнопке и будет запускать макрос на выполнение.

Создание макросов с использованием MacroRecorder я и называю программированием без программирования. Макросы играют двоякую роль. Они полезны, когда задачу, которую в принципе можно решить без программирования, приходится решать многократно. Не менее важно, что макросы можно использовать для обучения программированию, в частности, использованию объектов Office и VBA.

Часто трудно выбрать, как лучше запрограммировать решение некоторой задачи. Если это можно сделать вручную, то есть смысл создать макрос и посмотреть, как MacroRecorder решает подобную задачу. Анализ текста макросов напоминает мне исследование под микроскопом, — открывается масса неизвестных деталей.

Как работает машина вычислений Excel

Коль речь идет об основах программирования в Excel , то хочу попытаться достаточно точно описать семантику Excel , — как в нем проводятся вычисления. Как я уже говорил, документ Excel является рабочей книгой, каждый рабочий лист которой представляет конечную прямоугольную таблицу, элементы которой называются ячейками.

Листы книги, строки, столбцы таблицы и сами ячейки изначально именованы. В любой части этой таблицы можно выделить некоторую подобласть, обычно, прямоугольный интервал ячеек и с ним работать. Пожалуй, удобнее сразу перейти к объектной терминологии.

Замечу, одним из основных объектов Excel является объект Range . Ячейки, строки, столбцы, сама таблица целиком, любые ее подобласти, в том числе и не смежные, полученные, как пересечение или объединение интервалов — все это представимо единственным объектом Range . О многих свойствах и методах этого объекта будет рассказано в главе 3, посвященной объектам Excel . О некоторых скажу сейчас, рассматривая семантику вычислений . Благодаря тому, что объект Range имеет свойство Name , можно давать собственные имена используемым объектам, в том числе и ячейкам. Более важно, что объект Range имеет свойства Value и Formula . Свойство Value позволяет задать значение объекта, любого допустимого типа.

Здесь существенно используются возможности универсального типа Variant , с которым совместим тип Range . Свойство Formula позволяет связать с объектом формулу, вычисляющую значение . Поскольку Excel позволяет работать с массивами, то можно вводить и специальный класс формул — формулы над массивами. Во многом возможности Excel определяются тем, насколько широк класс задаваемых формул. Формулы строятся из констант, переменных, роль которых играют объекты Range, и стандартных функций, объединенных знаками операций. Я уже говорил, сколь велик выбор стандартных функций, как общего назначения, так и ориентированных на конкретные предметные области, прежде всего финансы и статистику. Допустимо использование в формулах и функций, разработанных на VBA программистом.

Поскольку формула, записанная в одной ячейке, может ссылаться на другие ячейки таблицы, то между ячейками возникает отношение зависимости. Дадим точные формулировки: Если формула в ячейке Y содержит ссылку на ячейку X, то говорят, что Y непосредственно зависит от X, а X непосредственно предшествует Y. Обобщая понятие непосредственной зависимости, мы говорим, Y зависит от X, а X предшествует Y, если существует цепочка ячеек Z1, Z2, …ZK, начинающаяся с X и заканчивающаяся Y, такая, что каждые два соседние элемента цепочки связаны отношением непосредственной зависимости (непосредственного предшествования). Свойства Dependents и Precedents объекта Range сохраняют списки всех его зависимых и соответственно предшествующих ячеек. Это позволяет с одной стороны графически отображать на экране зависимости между ячейками и, что более важно, эффективно организовать вычисления при изменении значений в тех или иных ячейках.

Однако Excel не всегда в состоянии определить, существует ли зависимость между ячейками. Пусть, например, в ячейку A1 введено значение 2 , в ячейку B1- 7 , в ячейку B2 — формула » =A1+B1 «, а в ячейку A2 — формула » = myfunct1(B1) «, где myfunct1(X) — собственная функция , заданная программой:

Public Function myfunct1(X As Variant) As Variant ‘Функция принимает объект Range в качестве параметра ‘и использует объект Range(«A1») как глобальную переменную. myfunct1 = Range(«A1»).Value + X.Value End Function

Excel может определить, что ячейка B2 зависит от ячеек A1 и В1. Но он не распознает, что ячейка A2 также зависит от A1, он обнаружит только ее зависимость от B1.

Причина в том, что Excel не анализирует тексты пользовательских функций, используемых в формулах, на наличие в них ссылок на ячейки таблицы. Не из-за того, что его разработчики поленились это сделать, но потому, что эта задача алгоритмически неразрешима в общем случае. Для определения отношения зависимости одной ячейки от другой используются лишь явные ссылки в параметрах вызываемых функций (B1 для ячейки A2 в нашем примере). Увидеть связи между ячейками можно на рисунке 1.1, где показан общий вид первого листа книги CourseFirst, с которой мы будем работать в ближайшее время.

Источник: intuit.ru