В данных методических указаниях рассматриваются вопросы применения средств языка Паскаль и средств Mathcad PLUS 6.0 для работы с матрицами.
Разбираются функции для обычных в линейной алгебре действий с матрицами.
В конце методических указаний даны задачи для самостоятельного решения.
Методические указания предназначены для студентов, выполняющих лабораторные работы по курсу “Информатика”, и имеют целью разработать основные навыки программирования математических и инженерных задач.
1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Матрицы — это строительные блоки важного класса математических моделей. Аппарат матриц позволяет более просто представлять различные математические и физические операции с помощью числовых операций над элементами матриц.
Примеры: матричные представления операторов квантовой механики, графов, задачи линейного программирования, теория линейных цепей, теория линейных колебаний, механика твердого тела и т.д.
2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
2.1. Определение матрицы
Паскаль с нуля [ч14]. Многомерные (двумерные) массивы
Матрица представляет собой прямоугольную таблицу чисел, расположенных строками и столбцами.
Она записывается следующим образом:
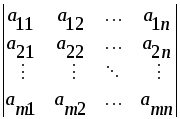
Вышеприведенная таблица называется (m ´ n) — матрицей, так как она имеет m — строк и n — столбцов.
Так как матрица представляет двухмерную таблицу чисел, то для обозначения каждого из ее элементов необходимо использовать двойные индексы. По условию, первый индекс обозначает номер строки, а второй — номер столбца. Любая матрица, имеющая одинаковое число строк и столбцов, называется квадратной матрицей. Квадратная матрица, имеющая n строк и n столбцов, называется матрицей n — го порядка.
Матрицы обычно обозначаются прописными латинскими буквами (A, B и т.д.), а элементы матриц — строчными латинскими буквами (aij, bij и т.д.).
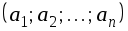
Вектор A является упорядоченной совокупностью n чисел, записанных либо строкой , либо столбцом
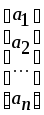
где ai, i=1. n являются действительными числами и называются компонентами вектора A.
2.2. Операции над матрицами
Операции над матрицами — это операции над таблицами чисел.
2.2.1. Равенство. Две матрицы А и B называются равными, обозначают A=B, если они идентичны, другими словами, если равны их соответствующие компоненты, т.е. aij = bij для каждых i,j.
2.2.2. Умножение на скаляр. Пусть дана матрица А и скаляр l. Произведение l×А, по определению является матрица

Каждый элемент матрицы А умножен на скаляр l.
2.2.3. Сложение. Суммой матрицы А, имеющей m строк и n столбцов и матрицы B, имеющей m строк и n столбцов, называется матрица С, элементы которой равны
cij = aij + bij (для всех i,j).
Ввод и вывод матриц на языке Pascal
Это можно записать:
Две матрицы суммируются сложением соответствующих элементов.
2.2.4. Вычитание. Определяется через уже рассмотренные действия:
A — B = A +(-1) ×B
Вычитание двух матриц сводится к вычитанию соответствующих элементов этих матриц.
2.2.5. Умножение. Произведением (m´n) — матрицы А и (n´r) — матрицы B (записывается A×B) называется матрица C, элементы которой получаются из элементов матрицы А и В по следующей формуле:

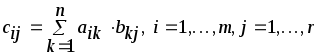
Матрица А допускает умножение на матрицу В и дает произведение А×В в том и только том случае, когда число столбцов в матрице А совпадает с числом строк в матрице В. Произведение С = А×В имеет одинаковое число строк с матрицей А и одинаковое число столбцов с матрицей В.
2.2.6. Транспонирование. Матрицей, транспонированной к матрице А, является матрица, образованная из матрицы А заменой i-й строки матрицы А ее i-м столбцом.
Транспонирование обозначается через А Т , т.е.
А Т = ½ a ji ½, когда А = ½ aij ½.
Можно заметить, что если А является (m´n) — матрицей, то А Т является (n´m) — матрицей.
2.2.7. Степень матрицы. Матрица А n равна произведению
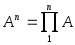
Возведение в степень n сводится к n операциям умножения.
2.3. Специальные виды матриц
2.3.1. Диагональная матрица. Диагональной называется матрица, все элементы которой равны 0, кроме тех, что расположены на главной диагонали.
2.3.2. Единичная матрица — это диагональная матрица, все элементы которой равны 1.
2.3.3. Нулевая матрица — это матрица, все элементы которой равны 0.
2.4. След матрицы
Следом квадратной матрицы порядка n является сумма
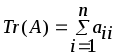
ее диагональных элементов.
3. ПРИМЕНЕНИЕ СРЕДСТВ ЯЗЫКА ПАСКАЛЬ ДЛЯ РАБОТЫ
3.1. Определение матрицы на языке Паскаль
Типы данных в Паскале делятся на класс простых типов и класс структурированных типов (структур).
Матрица — это переменная, имеющая структуру массива (двухмерный массив), представляющего собой совокупность компонент переменных одного и того же типа. Массив, как и любую другую структуру, необходимо описать и только затем использовать.
Описание массива осуществляется с использованием служебного слова array.
имя = array (тип индекса) of (тип компонент);
Определяется тип данных массив, а затем определяется переменная этого типа. Определение двухмерного массива (матрицы):
matrix=array[1..n,1..n] of real;
1. Каждая компонента массива может быть явно обозначена и к ней имеется прямой доступ.
2. Число компонент массива определяется при его описании и в дальнейшем не меняется.
В Паскале число элементов массива должно быть задано заранее. Если необходимо использовать массивы переменной размерности, то приходится описывать массивы с максимально возможным в данной задаче числом элементов, а затем использовать только часть из этих элементов.
Каждый элемент массива имеет свой порядковый номер, называемый индексом элемента в массиве. Индексы массива могут быть любого порядкового типа, чаще — целочисленного. Для матрицы необходимо задавать два индекса — индекс для строки и индекс для столбца.
При работе с матрицами можно выделить два класса задач: задачи с использованием одной матрицы и задачи, в которых осуществляются матричные операции над несколькими матрицами.
3.2. Работа с одной матрицей на языке Паскаль
Сформировать квадратную матрицу А порядка n, элементы которой aij определяются с помощью функции f(i,j)= i+j. Найти минимальный элемент, максимальный элемент и след матрицы. Полученные результаты распечатать.
Для формирования элементов матрицы используются два вложенных цикла for , в которых каждому элементу матрицы присваивается значение функции
A[i,j]:=i+j;
Для нахождения минимального элемента необходимо ввести переменную min, а для определения строки и столбца, в которой этот элемент находится, введем переменные imin и jmin. Переменной min присваиваем значение
min:=A[1,1]; imin:=1; jmin:=1;
Для нахождения максимального элемента введем переменные max, imax и jmax. Поиск максимального элемента осушествляется аналогично, только при сравнении используется неравенство A[i,j] > max.
Для нахождения следа матрицы (cм. 2.4) введем переменную tr, в которой накопим сумму всех элементов, находящихся на главной диагонали.
Для выдаче на печать матрицы используются два вложенных цикла for . Матрицу печатаем в привычном виде (1 строка матрицы — 1 строка экрана).
условием A[i,j]=f(i,j). Находит максимальный, минимальный элемент
и след матрицы. Все полученные результаты выдаются на печать >
A:array[1..10,1..10] of integer;
Writeln(‘Введите порядок матрицы n<10’);
if A[i,j] > max then
Writeln(‘Максимальный элемент =’,max:4,’ i=’,imax:2,’ j=’,jmax:2);
Writeln(‘Минимальный элемент =’,min:4,’ i=’,imin:2,’ j=’,jmin:2);
Writeln(‘След матрицы =’,tr:6);
3.3. Матричные операции на языке Паскаль
При решении этого класса задач важно отметить, что одни и те же операции производятся с несколькими матрицами, поэтому типовые операции с матрицами лучше оформить в виде процедур и использовать эти процедуры при решении задачи. Определим типовые процедуры для работы с матрицами: ввод матрицы, печать матрицы, умножение матрицы на скаляр, транспонирование матрицы, сложение матриц, умножение матриц. Операцию вычитания матриц (А-В) сведем к двум операциям: операция умножение матрицы В на скаляр (-1) и операция сложения двух матриц:
А-В= А + (-1) ×В
Возведение в степень n сводится к n операциям умножения матрицы А (см. 2.2.7).
Ввести значения элементов квадратной матрицы А порядка n и полученную матрицу вывести в привычном виде (1 строка матрицы — 1 строка экрана). Ввод и вывод матрицы оформить в виде процедуры.
Процедуры ввода и вывода матрицы должны содержать в качестве параметров: порядок матрицы, идентификатор, которой выдается при вводе или выводе и имя матрицы. Перед вводом элемента на экран выводится поясняющий текст, в котором кроме индексов очередного элемента матрицы выдается и имя матрицы (ее идентификатор). При выводе перед каждым элементом выводится имя матрицы, индексы элемента, а затем значение элемента. Максимальный порядок матрицы, с которой можно работать, задается с помощью константы NN (в данном случае NN=10). При работе с матрицами большей размерности надо увеличить значение этой константы. Если матрица используется в качестве параметра процедуры, то для нее надо дать явное определение типа:
Type Matr=array[1..NN,1..NN] of real ;
и при описании параметра в заголовке процедуры указать этот тип.
Type Matr=array[1..NN,1..NN] of real ;
Источник: studfile.net
Как задать матрицу в программе в паскаль
: 20
создание матриц паскаль
Только начала изучение матриц в паскале и что то не очень получается их задавать. нужно такую создать матрицу А=|a ij |, где i изменяется от 0 до N-1, j — от 0 до N-1. Числа должны вводится случайным образом.
Вот что пока получилось:
var i,j: integer; a:array [1..n,1..m] of integer; begin randomize; writeln(‘vvedite kollichestvo strok’); readln(n); writeln(‘vvedite kollichestvo stolbcov’; readln(m); for i:=1 to n do for j:=1 to m do begin write(‘ A[‘,i,j,’]’); readln (a[i,j]); end; for i:=1 to n do begin for j:=1 to n do write (a[i,j]); writeln; end; end.
Или может литературу какую посоветуете почитать.
Последний раз редактировалось Stilet; 28.03.2015 в 08:18 .
Источник: www.programmersforum.ru
Паскаль. Заполнить матрицу 3х3 случайными числами

На данном уроке рассмотрим, как работает матрица(двумерный массив) на языке программирования Паскаль.
Матрица — это двумерный массив, каждый элемент которого имеет два индекса: номер строки и номер столбца.
Program matrica;//Заполнить матрицу 3х3 случайными числами var a:array[1..3,1..3] of integer; i,j:integer; begin randomize; for i:=1 to 3 do for j:=1 to 3 do a[i,j]:=random(9); for i:=1 to 3 do begin for j:=1 to 3 do write(a[i,j],’ ‘); writeln; end; end.
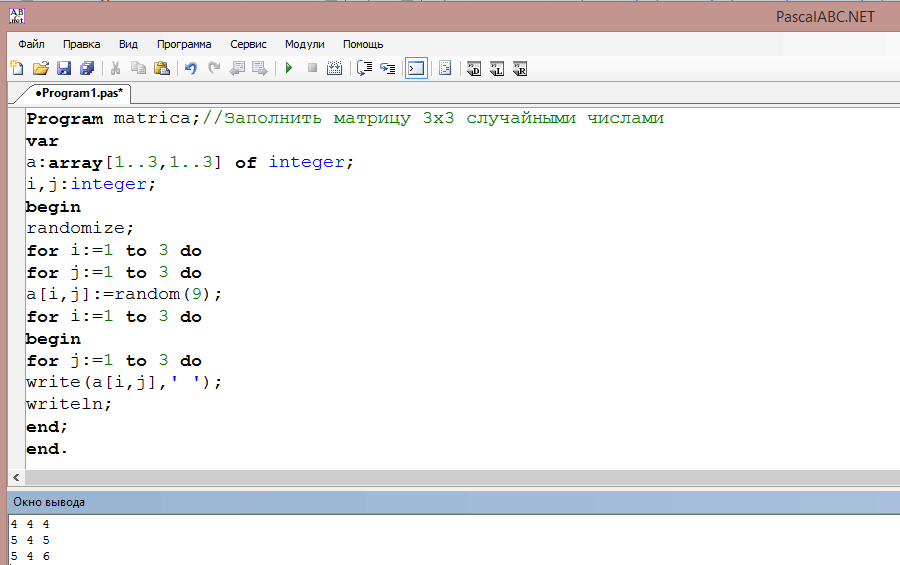
Самостоятельная работа
Заполнить матрицу 5х5 случайными числами. Найти минимальный и максимальный элемент матрицы.
Ответ напишите в комментариях этого поста
1 5 451 просмотров
Вам также может быть интересно

Уроки 0 7 456 просмотров
Упростить логические выражения Тема: «Алгебра логики» В некоторых заданиях ЕГЭ по информатике под №

Уроки 0 1 844 просмотров
Установка Python в связке с PyCharm Edu Все большую популярность среди профессиональных программистов и

Уроки 0 21 256 просмотров
Определение информационного объема сообщения. Информатика в 7 классе. Тема: «Измерение информации» Формулы Для определения
Источник: amlesson.ru