Граф – абстрактная структура данных, которая состоит из набора вершин и соединений между ними – ребер. При этом каждое ребро может иметь вес.
Рассмотрим реализацию простого графа с возможностью добавления вершин и ребер.
Ребро графа
Класс описывающий ребро графа.
/// /// Ребро графа /// public class GraphEdge < /// /// Связанная вершина /// public GraphVertex ConnectedVertex < get; > /// /// Вес ребра /// public int EdgeWeight < get; > /// /// Конструктор /// /// Связанная вершина /// Вес ребра public GraphEdge(GraphVertex connectedVertex, int weight) < ConnectedVertex = connectedVertex; EdgeWeight = weight; >>
Вершина графа
Класс описывает вершину графа, с возможностью добавления списка связанных вершин.
/// /// Вершина графа /// public class GraphVertex < /// /// Название вершины /// public string Name < get; > /// /// Список ребер /// public List Edges < get; > /// /// Конструктор /// /// Название вершины public GraphVertex(string vertexName) < Name = vertexName; Edges = new List(); > /// /// Добавить ребро /// /// Ребро public void AddEdge(GraphEdge newEdge) < Edges.Add(newEdge); >/// /// Добавить ребро /// /// Вершина /// Вес public void AddEdge(GraphVertex vertex, int edgeWeight) < AddEdge(new GraphEdge(vertex, edgeWeight)); > /// /// Преобразование в строку /// /// Имя вершины public override string ToString( ) => Name; >
Граф
Класс описывающий граф с методами добавления вершин и ребер.
Способы задать граф. Матрица векторов смежности
/// /// Граф /// public class Graph < /// /// Список вершин графа /// public List Vertices < get; > /// /// Конструктор /// public Graph( ) < Vertices = new List(); > /// /// Добавление вершины /// /// Имя вершины public void AddVertex(string vertexName) < Vertices.Add(new GraphVertex(vertexName)); > /// /// Поиск вершины /// /// Название вершины /// Найденная вершина public GraphVertex FindVertex(string vertexName) < foreach (var v in Vertices) < if (v.Name.Equals(vertexName)) < return v; > > return null; > /// /// Добавление ребра /// /// Имя первой вершины /// Имя второй вершины /// Вес ребра соединяющего вершины public void AddEdge(string firstName, string secondName, int weight) < var v1 = FindVertex(firstName); var v2 = FindVertex(secondName); if (v2 != null v1 != null) < v1.AddEdge(v2, weight); v2.AddEdge(v1, weight); >> >
Источник: programm.top
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Программа для построения графов C#
Представляем вашему вниманию программу для построения графов, написанную на языке C#. Внизу страницы вы можете скачать исходник этой программы, а в этой статье будут описаны функции программы и основные приемы, использовавшиеся при их кодировании.
Графы
Структура пользовательского интерфейса
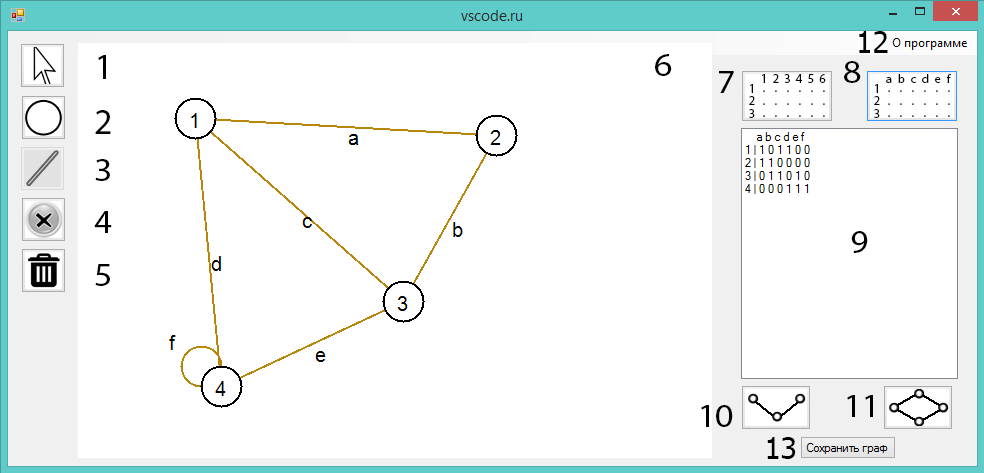
Рисунок 1. Пользовательский интерфейс программы
Пользовательский интерфейс программы изображен на рисунке 1. На нем цифрами обозначены элементы управления:
- Выбор вершины (при выборе какой-либо вершины, отображается ее степень).
- Создание вершины.
- Создание ребра.
- Удаление элемента.
- Удаление всего графа.
- Рабочее поле для построения графа.
- Построение матрицы смежности.
- Построение матрицы инцидентности.
- Поле для вывода информации о графе: степень выбранной вершины, матриц смежности и инцидентности, элементарных цепей и циклов.
- Вывод всех элементарных цепей.
- Вывод всех элементарных циклов.
- Информация о программе (окно представлено на рисунке 2).
- Сохранение изображения графа.
Если при построении ребра вы выбрали не ту вершину, то отменить выбор можно, нажав правой кнопкой мыши на выбранной вершине.

Рисунок 2. Окно «О программе»
Описание структуры программы
Опишем ключевые моменты в программном коде.
При кодировании граф был представлен в виде списка (List<>) экземпляров класса Vertex (вершина):
class Vertex
public int x , y ;
public Vertex ( int x , int y )
this . x = x ;
this . y = y ;
где x и y — координаты центра вершины.
И списка (List<>) экземпляров класса Edge (ребро):
class Edge
public int v1 , v2 ;
public Edge ( int v1 , int v2 )
this . v1 = v1 ;
this . v2 = v2 ;
v1 и v2 — номера вершин, которые соединяет ребро.
Когда происходит выбор вершины мышью, поиск нужной вершины из списка осуществляется посредством перебора всех вершин и проверки условия принадлежности точки, в месте щелчка мыши, окружности вершины с помощью уравнения окружности: (x — x0) 2 + (y — y0) 2 = R 2 .
for ( int i = 0 ; i < V . Count ; i ++ )
if ( Math . Pow ( ( V [ i ] . x — e . X ) , 2 ) + Math . Pow ( ( V [ i ] . y — e . Y ) , 2 ) < = G . R * G . R )
где e.X, e.Y — координаты точки в месте щелчка мыши, а G.R — радиус окружности вершины.
Заполнение матрицы смежности:
public void fillAdjacencyMatrix ( int numberV , List < Edge >E , int [ , ] matrix )
for ( int i = 0 ; i < numberV ; i ++ )
for ( int j = 0 ; j < numberV ; j ++ )
matrix [ i , j ] = 0 ;
for ( int i = 0 ; i < E . Count ; i ++ )
matrix [ E [ i ] . v1 , E [ i ] . v2 ] = 1 ;
matrix [ E [ i ] . v2 , E [ i ] . v1 ] = 1 ;
numberV — количество вершин в графе. matrix имеет размер [numberV, numberV].
Заполнение матрицы инцидентности:
public void fillIncidenceMatrix ( int numberV , List < Edge >E , int [ , ] matrix )
for ( int i = 0 ; i < numberV ; i ++ )
for ( int j = 0 ; j < E . Count ; j ++ )
matrix [ i , j ] = 0 ;
for ( int i = 0 ; i < E . Count ; i ++ )
matrix [ E [ i ] . v1 , i ] = 1 ;
matrix [ E [ i ] . v2 , i ] = 1 ;
где numberV — количество вершин в графе. matrix имеет размер [numberV, E.Count].
Определение степени вершины происходит в результате суммирования элементов строки матрицы смежности с номером, равным номеру выбранной вершины.
Если нажата кнопка «удаление элемента», то при щелчке мышью на рабочем поле происходит перебор всех элементов графа и поиск элемента, которому принадлежит координата в месте щелчка. При этом для ребер и петель поиск осуществляется с допуском в несколько пикселей, то есть, например, принадлежность точки, в месте щелка, конкретному ребру характеризуется принадлежностью точки области, границами которой выступают прямые, отстоящие вверх и вниз от исходной прямой на несколько пикселей.
Проиллюстрировать вышесказанное можно с помощью рисунка:
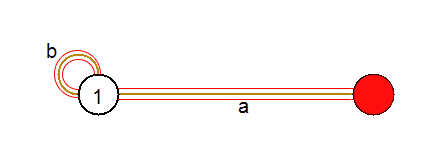
Рисунок 3. Области, рассматриваемые при поиске элемента графа для удаления
Красным цветом обозначен тот самый допуск в несколько пикселей при поиске элемента для удаления. Для вершины никакого допуска рассматривать не нужно.
Про поиск элементарных цепей и циклов мы уже рассказывали на vscode.ru. Почитать можно здесь:
Скачать исходник программы, написанной в Visual Studio, можно, нажав на кнопку ниже.
Источник: vscode.ru
Введение в теорию графов в Python

Теория графов — обширная область исследования, основанная на простой идее об отдельных точках, известных как вершины, соединенных линиями, известными как ребра, каждая из которых может иметь связанные числовые значения, называемые весом, а также, возможно, направлением.
Эти простые наборы вершин, ребер, весов и направлений известны как графы (не путать с более знакомым графом данных или математической функцией) и могут использоваться для представления многих реальных ситуаций или абстрактных концепций. Если у вас есть граф, хранящийся в какой-то структуре данных, существует множество алгоритмов, которые можно применять для решения проблем, особенно задач оптимизации.
Этот пост является первым из многих, и в нем я разработаю структуру данных для хранения графика. В будущих публикациях я буду реализовывать некоторые алгоритмы, работающие с графами.
Практическое использование
Наиболее очевидное использование графиков — это представление географических местоположений и маршрутов между ними. На приведенном ниже графике представлены четыре шотландских города, а линии и числа представляют соединения и расстояния (в милях) между ними.

Вероятно, самая известная проблема в теории графов — это проблема коммивояжера. В этой задаче гипотетическому продавцу необходимо как можно более эффективно посетить несколько городов. Есть шесть возможных комбинаций — какую выбрать, чтобы минимизировать расстояние или время?
Это проблема для будущей публикации, но сейчас нам нужно создать структуру данных для хранения графа, и я начну с написания класса для этого.
Структуры данных графиков
Большая часть данных может быть легко помещена в какую-либо структуру строки / столбца, в Python это может быть список списков, словарь кортежей, какая-либо другая их комбинация или, возможно, ваши собственные пользовательские структуры данных. Графики немного запутаннее, но есть два основных способа их представить.
Первый называется списком смежности, и я буду использовать его здесь. Он состоит из списка вершин (например, городов), каждая из которых содержит список ребер (например, список других городов, с которыми он связан, с указанием расстояния).
График шотландских городов, который я буду использовать в этом проекте, будет выглядеть так, когда он представлен в списке смежности.

Здесь стоит отметить несколько моментов. Во-первых, каждое ребро существует дважды, например, есть ребро от Инвернесса до Абердина с весом (расстоянием) 103, а также одно ребро от Абердина до Инвернесса с таким же весом. Край не направлен, но, опуская одно из этих ребер, мы можем представить направленный край, например улицу с односторонним движением.
Во-вторых, в этом примере все города связаны со всеми остальными. Если бы мы добавили все города, поселки и деревни в Шотландии, ни один из них не был бы связан со всеми остальными; фактически у большинства из них были бы прямые дороги только к горстке других. Использование списка смежности эффективно, поскольку в нем должны храниться только фактические ребра.
Это подводит нас ко второму основному типу структур данных, используемых для представления графиков, матрице смежности. Это двухмерная сетка, которая выглядит так:

В этом случае память тратится мало, но если бы такая структура данных использовалась для представления всех городов, поселков и деревень в Шотландии, большая часть памяти была бы потрачена впустую. Поэтому списки смежности подходят только в том случае, если большинство или все вершины соединены.
Проект
Этот проект состоит из следующих четырех файлов, находящихся в репозитории Github.
- vertex.py
- edge.py
- graphadjacencylist.py
- graphtheory.py
Во-первых, есть пара очень простых классов для представления вершин и ребер. Это Vertex класс.
Помимо label , Vertex имеет список ребер, а также атрибут под названием visited , который будет использоваться в будущем для различных алгоритмов.
Класс Edge имеет атрибуты для (т. Е. Вершины, к которой он относится) и веса. Начальная вершина — это вершина, к которой прикреплено ребро.
Теперь давайте посмотрим на класс GraphAdjacencyList , основу этого проекта.
__в этом__
Ну, это красиво и просто, не так ли? Просто создайте пустой список.
__str__
Довольно утомительный, но важный метод, который обеспечивает аккуратное строковое представление объекта, в первую очередь для нас с помощью функции печати.
В приведенной выше таблице, демонстрирующей матрицу смежности, я показал края каждой вершины по горизонтали, но здесь они показаны вертикально, как мы сейчас увидим. Если у вершины нет ребер или если ребро не имеет веса, то отображаются пробелы.
add_vertex
Сначала мы проверяем, что вершина с данной меткой еще не существует, и, если нет, создается и добавляется новый объект Vertex.
add_edge
Нам нужно проверить, что ребро еще не существует, а также, что заданные метки вершин действительно существуют, что при необходимости вызывает ошибки. Если все в порядке, мы создаем новый объект Edge и добавляем его в вершину.
Если край не направлен, нам также необходимо добавить «обратный» край, что делается с помощью рекурсивного вызова add_edge. Этот вызов должен быть направлен на True, иначе метод попытается воссоздать первое ребро, что приведет к ошибке.
edit_vertex
Этот метод используется для переименования вершин, поэтому необходимо изменить атрибуты ребер на. Это делается путем перебора вершин и использования внутреннего цикла для перебора ребер. Обратите внимание, что возникает ошибка, если вершина с данной меткой не существует.
edit_edge
Этот метод изменяет веса ребер, перебирая вершины, чтобы найти вершину «от», а затем перебирая ее ребра, чтобы найти вершину «до». Если ребро не существует, возникает ошибка.
Обратный метод не работает: если есть еще ребро от вершины «до» к вершине «от», вес не меняется. Это сделано намеренно и допускает ситуации, когда веса различны в каждом направлении.
delete_vertex
Этот метод удаляет вершину с указанной меткой, а также все ребра в других вершинах, указывающие на нее. Обычно возникает ошибка, если вершина не существует.
delete_edge
Этот метод перебирает вершины, чтобы найти «от», а затем перебирает его ребра, чтобы найти «до», прежде чем удалять его. Как и в случае с edit_edge, метод не влияет на края в противоположном направлении.
__find_vertex_index
Это служебная функция, которая находит индекс вершины с заданной меткой, если таковой имеется.
__edge_exists
Эта функция проверяет, существует ли ребро между двумя заданными вершинами.
Наш GraphAdjacencyList класс завершен, поэтому нам просто нужно опробовать его в graphtheory.py.
В main мы сначала вызываем функцию для создания и заполнения графика данными о городах Шотландии, а затем распечатываем его.
Запустить программу
Запустите код с помощью этой команды…
… Что даст вам этот результат.

Функция edit_graph переводит названия городов на шотландский язык (Эдинбург на английском и на шотландском языках совпадает). Закомментируйте первый print в main , затем раскомментируйте вызов edit_graph и второй print . Запустите программу еще раз, и вы получите .

Я лишь поверхностно коснулся этой обширной темы, но теперь вы понимаете, что такое граф и какие структуры данных можно использовать для представления графа.
В следующих статьях я рассмотрю некоторые алгоритмы, которые можно применить к графу.
Источник: digitrain.ru