Как вычислить число пи программа

Use saved searches to filter your results more quickly

Cancel Create saved search

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window.

Reload to refresh your session.

Базовый набор алгоритмов для вычисления числа Пи

SovietModernism/basic-pi

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags

Nothing to show

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Cancel Create

• Local
• Codespaces

HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.

07. Быстрое вычисление числа π по Эйлеру

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

Latest commit message
Commit time

README.md

Каждая функция-алгоритм принимает на вход аргумент n — длину бесконечного ряда чисел, с помощью которого и вычисляется Пи. На практике это число означает количество итераций внутри определённого алгоритма — чем их больше, тем точнее будут вычисления, но и тем дольше время выполнения.

Помимо самих функций для подсчёта Пи, в проекте также присутствует 2 дополнительных метода: measure() и compare(). Первый измеряет скорость исполнения алгоритма, второй — точность вычисленного им значения (по знакам после запятой). Оба метода принимают в качестве аргументов само название функции и количество итераций n.

Все функции поддерживают как возврат значения, так и простой вывод результата.

В самом начале программы присутствует строка getcontext().prec = 100, отвечающая за точность после запятой в вещественных числах. Установленная точность распространяется не только на вычисленные значения Пи, но и вообще на бóльшую часть вычислений в программе, так как они происходят посредством библиотеки Decimal, для которой эта точность и определяется.

По-умолчанию точность стоит на 100 знаках после запятой (число Пи такой же точности используется и в функции compare(), чтобы сравнивать с ним результаты работы алгоритмов). Увеличение этого значения, вероятно, сделает вычисления более точными и медленными.

Число Пи: как найти его с точностью до 50 знака?

• ряд Лейбница

• формула Виета для приближения числа π

Источник: github.com

Вычисление числа Пи методом Монте-Карло

Существует много способов вычисления числа Пи. Самым простым и понятным является численный метод Монте-Карло, суть которого сводится к простейшему перебору точек на площади. Суть расчета заключается в том, что мы берем квадрат со стороной a = 2 R, вписываем в него круг радиусом R. И начинаем наугад ставить точки внутри квадрата. Геометрически, вероятность P1 того, чтот точка попадет в круг, равна отношению площадей круга и квадрата:
P1=Sкруг / Sквадрата = πR 2 / a 2 = πR 2 / (2 R ) 2 = πR 2 / (2 R) 2 = π / 4 (1)
Выглядит это так:

Вероятность попадания точки в круг можно также посчитать после численного эксперимента ещё проще: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
P2=Nпопавших в круг / Nточек; (2)
Так, при большом количестве точек в численном эксперименте вероятности должны вести себя cледующим образом:
lim(Nточек→∞)⁡(P2-P1)=0; (3)
Следовательно:
π / 4 = Nпопавших в круг / Nточек; (4)
π =4 Nпопавших в круг / Nточек; (5)
НО! При моделировании мы применяем псевдослучайные числа, которые не являются случайным процессом.
Поэтому, выражение (5), к сожалению, строго не выполняется. Логичны вопросы, каковы оптимальные размеры квадрата и как много нужно применить точек?
Чтобы это выяснить, я написал такую программу:

#include #include #define limit_Nmax 1e7 //Максимальное количество точек #define limit_a 1e6 //Максиальный радиус круга #define min_a 100 //Начальный радиус double circle(double, double); //Выдает квадрат y в зависимости от координаты Х и радиуса круга. int main() < double x,y,Pi; long long int a=min_a//сторона квадарата i=0;//Счетчик double Ncirc=0;//Количество точек, попавших в круг double Nmax=a; //Общее количество точек while (ai++; > Pi=(Ncirc/Nmax)*4; Nmax *= 2; printf(«n%lld,%.0f,%f»,a,Nmax,Pi); > a*=2; > > double circle(double x, double radius)

Программа выводит значения числа Пи в зависимости от радиуса и количества точек. Единственное, что остается читателю, это скомпилировать её самостоятельно и запустить с параметрами, которые желает он.

Приведу лишь одну таблицу с полученными значениями:

Радиус	Nточек	Pi
102400	204800	3,145664
102400	409600	3,137188
102400	819200	3,139326
102400	1638400	3,144478
102400	3276800	3,139875
102400	6553600	3,142611
102400	13107200	3,140872
102400	26214400	3,141644
102400	52428800	3,141217
102400	1,05E+08	3,141324
102400	2,1E+08	3,141615
102400	4,19E+08	3,141665
102400	8,39E+08	3,141724
102400	1,68E+09	3,141682

Если что, значение числа Пи можно посмотреть с точностью до определенного знака здесь.
Источник картинки — википедия.

• численные методы
• число пи
• Монте-Карло

Источник: habr.com

Mpi программа для вычисления числа π на языке с.

Для первой параллельной программы удобна программа вычисления числа π, поскольку в ней нет загрузки данных и легко проверить ответ. Вычисления сводятся к вычислению интеграла по следующей формуле:

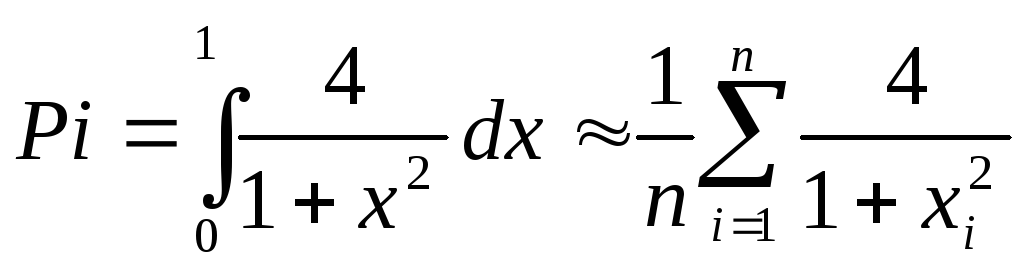
где xi = (i-1/2) / n. Программа :

int main ( int argc, char *argv[] )

int n, myid, numprocs, i; /* число ординат, имя и число процессов*/

double PI25DT = 3.141592653589793238462643; /* используется для оценки

double mypi, pi, h, sum, x; /* mypi – частное значение π отдельного процесса, pi –

полное значение π */

MPI_Init(argv); /* задаются системой*/

printf («Enter the number of intervals: (0 quits) «); /*ввод числа ординат*/

if (n == 0) /* задание условия выхода из программы */

h = 1.0/ (double) n; /* вычисление частного значения π некоторого процесса */

x = h * ( (double)i — 0.5);

sum += (4.0 / (1.0 + x*x));

mypi = h * sum; /* вычисление частного значения π некоторого процесса */

MPI_Reduce(pi, 1, MPI_DOUBLE, MPI_SUM, 0,

MPI_COMM_WORLD); /* сборка полного значения π */

if (myid == 0) /* оценка погрешности вычислений */

printf («pi is approximately %.16f. Error is

%.16fn», pi, fabs(pi — PI25DT));

MPI_Finalize(); /* выход из MPI */

Программа умножения матрицы на вектор

Результатом умножения матрицы на вектор является вектор результата. Для решения задачи используется алгоритм, в котором один процесс (главный) координирует работу других процессов (подчиненных). Для наглядности единая программа матрично-векторного умножения разбита на три части: общую часть , код главного процесса и код подчиненного процесса .

В общей части программы описываются основные объекты задачи: матрица А, вектор b, результирующий вектор с, определяется число процессов (не меньше двух). Задача разбивается на две части: главный процесс (master) и подчиненные процессы. В задаче умножения матрицы на вектор единица работы, которую нужно раздать процессам, состоит из скалярного произведения строки матрицы A на вектор b. Знаком ! отмечены комментарии.

integer MAX_ROWS, MAX_COLS, rows, cols

parameter (MAX_ROWS = 1000, MAX_COLS = 1000)

! матрица А, вектор b, результирующий вектор с

double precision a(MAX_ROWS,MAX_COLS), b(MAX_COLS), с(MAX_ROWS)

double precision buffer (MAX_COLS), ans /* ans – имя результата*/

integer myid, master, numprocs, ierr, status (MPI_STATUS_SIZE)

integer i, j, numsent, sender, anstype, row /* numsent – число посланных строк,

sender – имя процесса-отправителя, anstype – номер посланной строки*/

call MPI_INIT( ierr )

call MPI_COMM_RANK( MPI_COMM_WORLD, myid, ierr )

call MPI_COMM_SIZE( MPI_COMM_WORLD, numprocs, ierr )

! главный процесс – master

! количество строк и столбцов матрицы А

if ( myid .eq. master ) then

! код главного процесса

! код подчиненного процесса

Код главного процесса. Единицей работы подчиненного процесса является умножение строки матрицы на вектор.

! инициализация А и b

do 20 j = 1, cols

do 10 i = 1, rows

! посылка b каждому подчиненному процессу

call MPI_BCAST(b, cols, MPI_DOUBLE_PRECISION, master,

! посылка строки каждому подчиненному процессу; в TAG номер строки = i

do 40 i = 1,min(numprocs-l, rows)

do 30 j = I, cols

call MPI_SEND(buffer, cols, MPI_DOUBLE_PRECISION, i, i,

numsent = numsent + l

! прием результата от подчиненного процесса

do 70 i = 1, rows

! MPI_ANY_TAG – указывает, что принимается любая строка

call MPI_RECV(ans, 1, MPI_DOUBLE_PRECISION, MPI_ANY_SOURCE,

MPI_ANY_TAG, MPI_COMM_WORLD, status, ierr)

sender = status (MPI_SOURCE)

anstype = status (MPI_TAG)

! определяем номер строки

if (numsent .lt. rows) then

! посылка следующей строки

do 50 j = 1, cols

buffer(j) = a(numsent+l, j)

call MPI_SEND (buffer, cols, MPI_DOUBLE_PRECISION, sender,

numsent+l, MPI_COMM_WORLD, ierr)

! посылка признака конца работы

call MPI_SEND(MPI_BOTTQM, 0, MPI_DOUBLE_PRECISION,sender,

0, MPI_COMM_WORLD, ierr)

Сначала главный процесс передает вектор b в каждый подчиненный про-

цесс, затем пересылает одну строку матрицы A в каждый подчиненный процесс.

Главный процесс, получая результат от очередного подчиненного процесса, пе-

редает ему новую работу. Цикл заканчивается, когда все строки будут розданы

и получены результаты.

При передаче данных из главного процесса в параметре tag указывается

номер передаваемой строки. Этот номер после вычисления произведения вме-

сте с результатом будет отправлен в главный процесс, чтобы главный процесс

знал, где размещать результат.

Подчиненные процессы посылают результаты в главный процесс и пара-

метр MPI_ANY_TAG в операции приема главного процесса указывает, что

главный процесс принимает строки в любой последовательности. Параметр

status обеспечивает информацию, относящуюся к полученному сообщению. В

языке Fortran это – массив целых чисел размера MPI_STATUS_SIZE. Аргу-

мент SOURCE содержит номер процесса, который послал сообщение, по этому

адресу главный процесс будет пересылать новую работу. Аргумент TAG хра-

нит номер обработанной строки, что обеспечивает размещение полученного ре-

зультата. После того как главной процесс разослал все строки матрицы А, на

запросы подчиненных процессов он отвечает сообщением с отметкой 0.

Код подчиненного процесса .

! прием вектора b всеми подчиненными процессами

call MPI_BCAST(b, cols, MPI_DOUBLE_PRECISION, master,

! выход, если процессов больше количества строк матрицы

if (numprocs .gt. rows) goto 200

! прием строки матрицы

90 call MPI_RECV(buffer, cols, MPI_DOUBLE_PRECISION, master,

MPI_ANY_TAG, MPI_COMM_WORLD, status, ierr)

if (status (MPI_TAG) .eq. 0) then go to 200

row = status (MPI_TAG)

! номер полученной строки

do 100 i = 1, cols

! скалярное произведение векторов

! передача результата головному процессу

! цикл для приема следующей строки матрицы

Каждый подчиненный процесс получает вектор b. Затем организуется цикл, состоящий в том, что подчиненный процесс получает очередную строку матрицы А, формирует скалярное произведение строки и вектора b, посылает результат главному процессу, получает новую строку и так далее.

Вопросы для самоконтроля

1. Стандарт MPI. Функции.

Источник: studfile.net