Критерий Манна-Уитни представляет непараметрическую альтернативу t -критерия для независимых выборок. Преимущество его состоит в том, что мы отказываемся от предположения нормальности распределения и одинаковых дисперсий. Необходимо, чтобы данные были измерены как минимум в порядковой шкале.
STATISTICA предполагает, что данные расположены тем же образом, что в и t -критерии для независимых выборок. Файл должен содержать кодовую (независимую) переменную, имеющую, по крайней мере, два разных кода для однозначной идентификации принадлежности каждого наблюдения к определенной группе.
Предположения и интерпретация. Критерий Манна-Уитни предполагает, что рассматриваемые переменные измерены, по крайней мере, в порядковой шкале (ранжированы). Интерпретация теста по существу похожа на интерпретацию результатов t -критерия для независимых выборок, за исключением того, что U критерий вычисляется, как сумма индикаторов попарного сравнения элементов первой выборки с элементами второй выборки. U критерий — наиболее мощная (чувствительная) непараметрическая альтернатива t-критерия для независимых выборок ; фактически, в некоторых случаях он имеет даже большую мощность, чем t -критерий.
Расчет критерия U Манна Уитни в SPSS
Если объем выборки больше 20, то распределение выборки для U статистики быстро сходится к нормальному распределению (см. Siegel, 1956). Поэтому вместе с U статистикой будут показаны z значение (для нормального распределения и соответствующее p -значение.
Точные вероятности для малых выборок. Для выборок малого объема STATISTICA вычислит точную вероятность, связанную с соответствующей U статистикой. Эта вероятность основана на подсчете всех возможных значений U при заданном количестве наблюдений в двух выборках (см. Dinneen фактически, в некоторых случаях он имеет даже большую мощность, чем t -критерий.
Если объем выборки больше 20, то распределение выборки для U статистики быстро сходится к нормальному распределению. Поэтому, вместе с U статистикой, будут показано z значение (для нормального распределения) и соответствующее p -значение.
Подробные инструкции по поводу того, как использовать критерий, вы можете найти дальше в части, касающейся примера применения.
Пример
Проверим гипотезу о принадлежности сравниваемых независимых выборок к одной и той же генеральной совокупности с помощью непараметрического U-критерия Манна-Уитни. Сравним результаты, полученные в примере Основные статистики и t-критерий Стьюдента для 2-го и 3-го столбцов таблицы по критерию Стьюдента, с результатами непараметрического сравнения.
Для расчета U-критерия Уилкоксона расположим варианты сравниваемых выборок в порядке возрастания в один обобщенный ряд и присвоим вариантам обобщенного ряда ранги от 1 до n1 + n2. Первая строка представляет собой варианты первой выборки, вторая — второй выборки, третья — соответствующие ранги в обобщенном ряду:
Источник: statistica.ru
U-критерий МАННА-УИТНИ в STATISTICA #03 | СТАТИСТИКА STATISTICA
5. Сравнение выборок с помощью критерия Манна-Уитни в приложении статистика.
Группируем данные обеих выборок в единый ряд и введем еще одну переменную — номер выборки: значениям признака из выборки 1 соответствует 1, значениям признака из выборки 2 – соответствует цифра 2 (ранее все это уже было проделано в Таблице 4).
Вставляем данные (оба столбца) в специальную таблицу Spreadsheet. Выбираем последовательно разделы Statistics-Nonparametrics/Comparing two independent samples (groups) (как показано на Рисунке 14).

В открывшейся вкладке (Рис. 15 ) указываем, в каком столбце находятся значения изучаемого признака (Dependent variables), в каком значения группирующей переменной (Grouping variables), в данном случае это номер выборки, и нажимаем кнопку Mann-Whitney U test.

Итоговая таблица содержит информацию о сумме рангов по каждой выборке, значение критерия Манна-Уитни, а также всевозможные оценки значимости различий между выборками. Различия между выборками достоверны, если уровень значимости (p-level) меньше 0,05.
Источник: studfile.net
Как выполнить U-тест Манна-Уитни в Stata
U- критерий Манна-Уитни (иногда называемый критерием суммы рангов Уилкоксона) используется для сравнения различий между двумя выборками, когда распределение выборки не является нормальным, а размеры выборки малы (n < 30). Он считается непараметрическим эквивалентомдвухвыборочного t-критерия .
В этом руководстве объясняется, как выполнить U-тест Манна-Уитни в Stata.
Пример: U-критерий Манна-Уитни в Stata
Исследователи хотят знать, приводит ли обработка топлива к изменению среднего расхода топлива на галлон автомобиля. Чтобы проверить это, они проводят эксперимент, в котором измеряют расход на галлон 12 автомобилей с обработкой топлива и 12 автомобилей без нее.
Поскольку размеры выборки малы и они подозревают, что распределение выборки не является нормальным, они решили выполнить U-критерий Манна-Уитни, чтобы определить, есть ли статистически значимая разница в милях на галлон между двумя группами.
Выполните следующие шаги, чтобы провести U-тест Манна-Уитни в Stata.
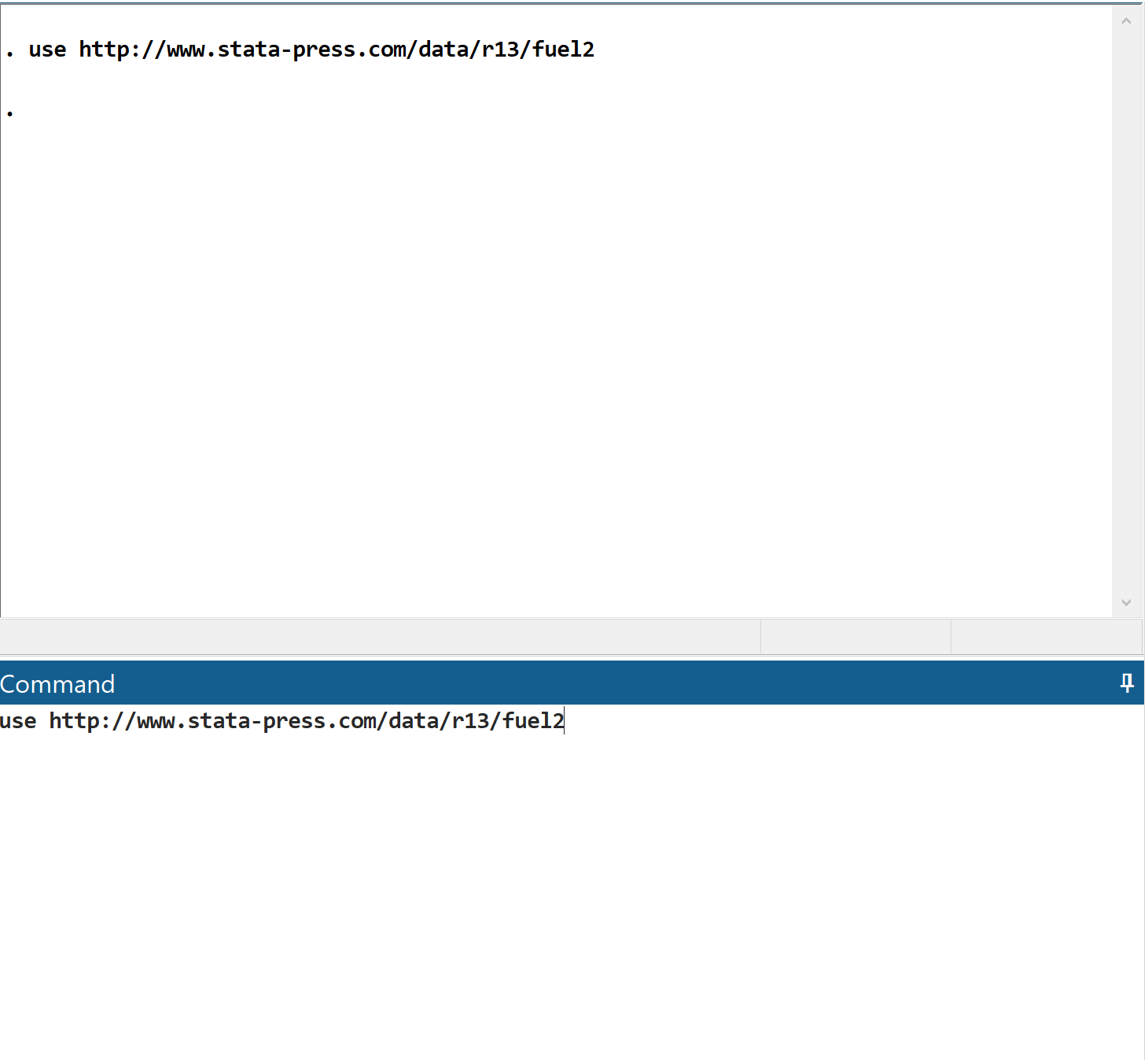
Шаг 1: Загрузите данные.
Сначала загрузите данные, введя use http://www.stata-press.com/data/r13/fuel2 в поле команды и нажав Enter.
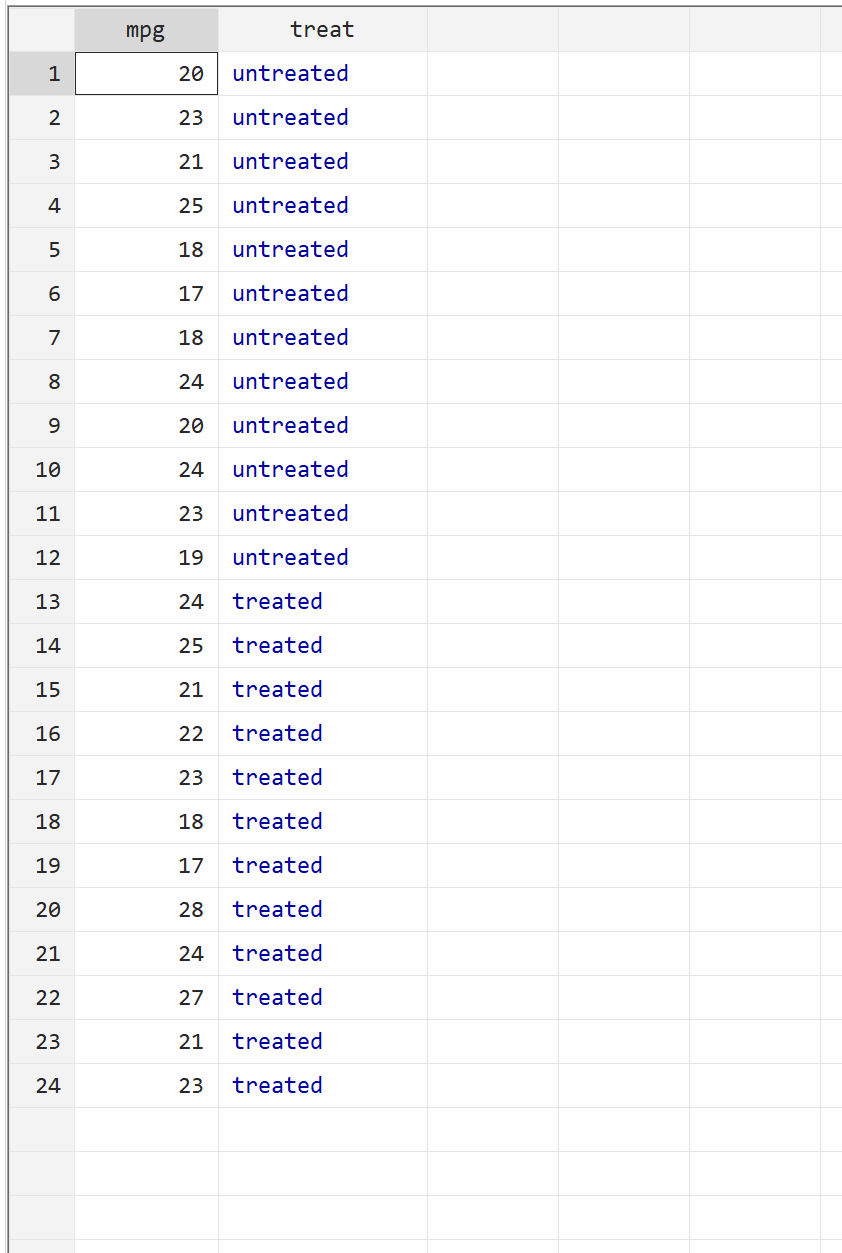
Шаг 2: Просмотрите необработанные данные.
Прежде чем мы выполним U-тест Манна-Уитни, давайте сначала просмотрим необработанные данные. В верхней строке меню выберите Данные > Редактор данных > Редактор данных (Обзор).Первый столбец, mpg , показывает количество миль на галлон для данного автомобиля, а второй столбец, treat , показывает, прошел ли автомобиль обработку топлива.
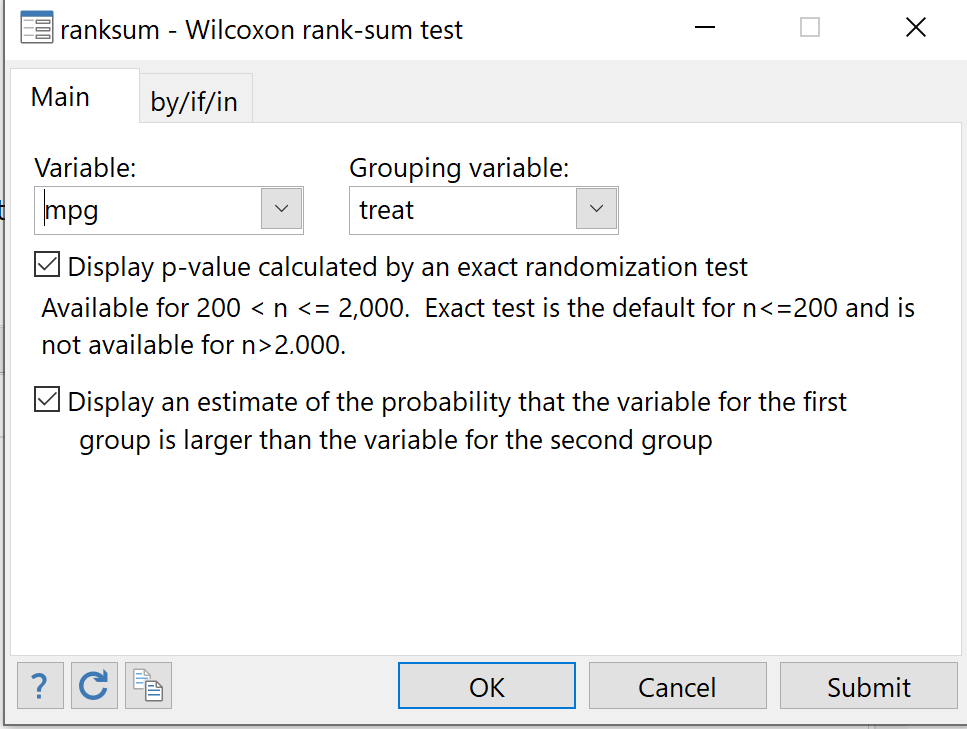
Шаг 3: Выполните U-критерий Манна-Уитни.
В верхней строке меню выберите Статистика > Сводки, таблицы и тесты > Непараметрические тесты гипотез > Критерий суммы рангов Вилкоксона .
В качестве переменной выберите mpg.Для группирующей переменной выберите трактовать.Установите оба флажка ниже, чтобы отобразить значение p для точного теста и отобразить оценку вероятности того, что переменная для первой группы больше, чем переменная для второй группы. Наконец, нажмите ОК .
Результаты теста будут отображены:
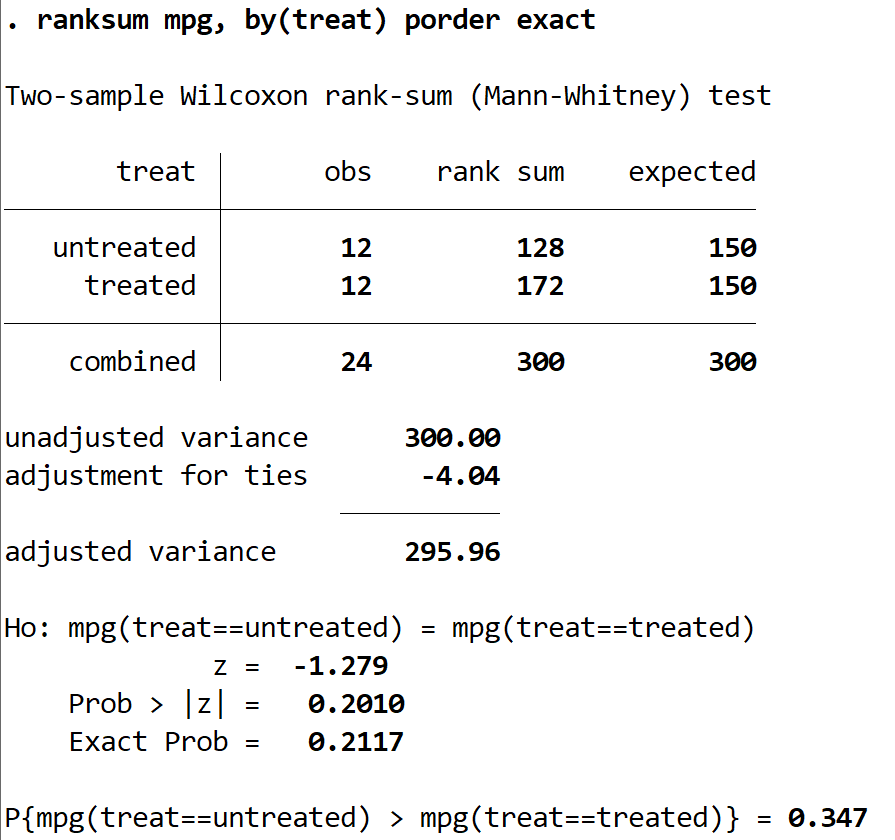
В первую очередь нас интересуют значения z = -1,279 и Prob > |z| = 0,2010.
Поскольку p-значение теста (0,2010) не меньше нашего уровня значимости 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что истинное среднее значение расхода на галлон отличается между двумя группами.
Шаг 5: Сообщите о результатах.
Наконец, мы сообщим о результатах нашего U-теста Манна-Уитни. Вот пример того, как это сделать:
Испытание Манна-Уитни U было проведено на 24 автомобилях, чтобы определить, приводит ли новая обработка топлива к разнице в среднем количестве миль на галлон. В каждой группе было по 12 автомобилей.
Результаты показали, что среднее количество миль на галлон статистически значимо не различалось между двумя группами (z = -1,279, p = 0,2010) при уровне значимости 0,05.
Основываясь на этих результатах, новая обработка топлива не оказывает существенного влияния на количество миль на галлон автомобилей.
Источник: www.codecamp.ru