Критерий Фишера применяется при проверке гипотезы о равенстве дисперсий двух генеральных совокупностей, распределенных по нормальному закону. Он является параметрическим критерием.
F-критерий Фишера называют дисперсионным отношением, так как он формируется как отношение двух сравниваемых несмещенных оценок дисперсий.
Пусть в результате наблюдений получены две выборки. По ним вычислены дисперсии и , имеющие и степеней свободы. Будем считать, что первая выборка взята из генеральной совокупности с дисперсией , а вторая – из генеральной совокупности с дисперсией . Выдвигается нулевая гипотеза о равенстве двух дисперсий, т.е. H0: или . Для того, чтобы отвергнуть эту гипотезу нужно доказать значимость различия при заданном уровне значимости .
Значение критерия вычисляется по формуле:
Очевидно, что при равенстве дисперсий величина критерия будет равна единице. В остальных случаях она будет больше (меньше) единицы.
Критерий имеет распределение Фишера . Критерий Фишера – двусторонний критерий, и нулевая гипотеза отвергается в пользу альтернативной если . Здесь , где – объем первой и второй выборки соответственно.
08 04 Сравнение двух выборок
В системе STATISTICA реализован односторонний критерий Фишера, т.е. в качестве всегда берут максимальную дисперсию. В этом случае нулевая гипотеза отвергается в пользу альтернативы , если .
Пример
Пусть поставлена задача, сравнить эффективность обучения двух групп студентов. Уровень успеваемости — характеризует уровень управления процессом обучения, а дисперсия качество управления обучением, степень организованности процесса обучения. Оба показателя являются независимыми и в общем случае должны рассматриваться совместно. Уровень успеваемости (математическое ожидание) каждой группы студентов характеризуется средними арифметическими и , а качество характеризуется соответствующими выборочными дисперсиями оценок: и . При оценке уровня текущей успеваемости оказалось, что он одинаков у обоих учащихся: = = 4,0. Выборочные дисперсии: и . Числа степеней свободы, соответствующие этим оценкам: и . Отсюда для установления различий в эффективности обучения мы можем воспользоваться стабильностью успеваемости, т.е. проверим гипотезу .
Вычислим (в числителе должна быть большая дисперсия), . По таблицам (STATISTICA – Probability Distribution Calculator) находим , которое меньше вычисленного, следовательно нулевая гипотеза должна быть отвергнута в пользу альтернативы . Это заключение может не удовлетворить исследователя, поскольку его интересует истинная величина отношения (у нас в числителе всегда большая дисперсия). При проверке одностороннего критерия получим , что меньше вычисленного выше значения. Итак, нулевая гипотеза должна быть отвергнута в пользу альтернативы .
Критерий Фишера в программе STATISTICA в среде Windows
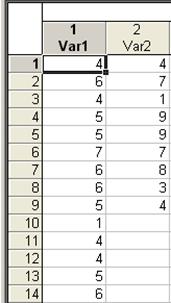
Для примера проверки гипотезы (критерий Фишера) используем (создаем) файл с двумя переменными (fisher.sta):
Т-критерий Стьюдента за 12 минут. Биостатистика.
Рис. 1. Таблица с двумя независимыми переменными
Чтобы проверить гипотезу необходимо в базовой статистике (Basic Statistics and Tables) выбрать проверку по Стьюденту для независимых переменных. (t-test, independent, by variables).
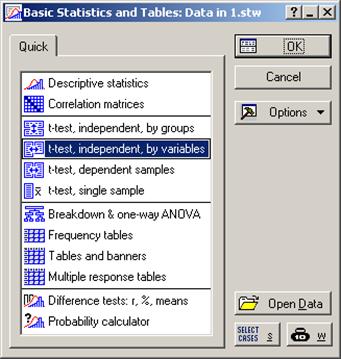
Рис. 2. Проверка параметрических гипотез
После выбора переменных и нажатия на клавишу Summary производится подсчет значений среднеквадратичных отклонений и критерия Фишера. Кроме этого определяется уровень значимости p, при котором различие несущественно.
Рис. 3. Результаты проверки гипотезы (F- критерий)
Используя Probability Calculator и задав значение параметров можно построить график распределения Фишера с пометкой вычисленного значения.
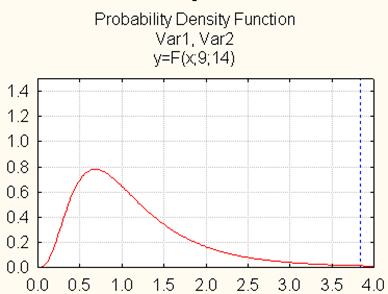
Рис. 4. Область принятия (отклонения) гипотезы (F- критерий)
Источники.
1. Проверка гипотез об отношениях двух дисперсий
2. Лекция 6. :8080/resources/math/mop/lections/lection_6.htm
3. F – критерий Фишера
4. Теория и практика вероятностно-статистических исследований.
5. F – критерий Фишера
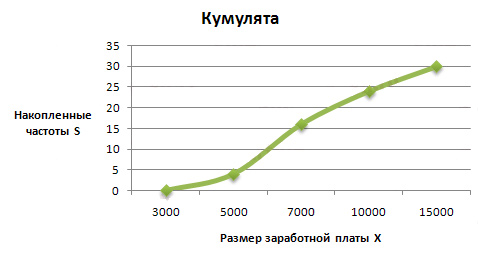
Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты.
Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости (рис. 6.3).
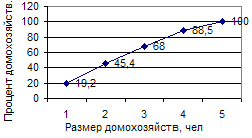
Рис. 6.3. Кумулята распределения домохозяйств по размеру
4. Рассчитаем накопленные частоты: Наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.
| Размер заработной платы руб в месяц Xi | Численность работников чел. fi | Накопленные частоты S |
| до 5000 | ||
| 5000 — 7000 | ||
| 7000 — 10000 | ||
| 10000 — 15000 | ||
| Итого: | — |
При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:
Огива
Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
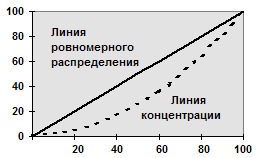
Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объёму признака.
Равномерному распределению признака соответствует на графике диагональ квадрата (рис. 6.4). При неравномерном распределении график представляет собой вогнутую кривую исходя из уровня концентрации признака.
12.Виды абсолютных и относительных показателей.
Статистический показатель — количественная характеристика социально-экономических явлений и процессов в условиях качественной определенности.
Различают показатель-категорию и конкретный статистический показатель:
Конкретный статистический показатель — это цифровая характеристика изучаемого явления или процесса. К примеру: численность населения России на данный момент составляет 145 млн.человек.
По форме различают статистические показатели:
- Абсолютные
- Относительные
- Средние
По охвату единиц различают индивидуальные и сводные показатели.
Индивидуальные показатели — характеризуют отдельный объект или отдельную единицу совокупности (прибыль фирмы, размер вклада отдельного человека).
Сводные показатели — характеризуют часть совокупности или в всю статистическую совокупность в целом. Их можно получить как объёмные и расчетные. Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Полученная величина принято называть объёмом признака. Расчетные показатели вычисляются по различным формулам и используются при анализе социально-экономических явлений.
Статистические показатели по временному фактору делятся на:
- Моментные показатели — отражают состояние или уровень явления на определенный момент времени. К примеру, число вкладов в Сбербанке на конец какого-либо периода.
- Интервальные показатели — характеризуют итоговый результат за период (день, неделя, месяц, квартал, год) в целом. К примеру, объём произведенной продукции за год.
Статистические показатели связаны между собой. По этой причине, чтообы составить целостное представление об изучаемом явлении или процессе, крайне важно рассматривать систему показателей.
2. Однофакторный дисперсионный анализ для несвязанных выборок
Назначение метода
Метод однофакторного дисперсионного анализа применяется в тех случаях, когда исследуются изменения результативного признака под влиянием изменяющихся условий или градаций какого-либо фактора. В данном варианте метода влиянию каждой из градаций фактора подвергаются разные выборки испытуемых. Градаций фактора должно быть не менее трех. (Градаций может быть и две, но в этом случае мы не сможем установить нелинейных зависимостей и более разумным представляется использование более простых).
Непараметрическим вариантом этого вида анализа является критерий Н Крускала-Уоллиса.
Гипотезы
H0: Различия между градациями фактора (разными условиями) являются не более выраженными, чем случайные различия внутри каждой группы.
H1: Различия между градациями фактора (разными условиями) являются более выраженными, чем случайные различия внутри каждой группы.
2.2. Ограничения метода однофакторного дисперсионного анализа для несвязанных выборок
1. Однофакторный дисперсионный анализ требует не менее трех градаций фактора и не менее двух испытуемых в каждой градации.
2. Результативный признак должен быть нормально распределен в исследуемой выборке.
Правда, обычно не указывается, идет ли речь о распределении признака во всей обследованной выборке или в той ее части, которая составляет дисперсионный комплекс.
3. Пример решения задачи методом однофакторного дисперсионного анализа для несвязанных выборок на примере:
Три различные группы из шести испытуемых получили списки из десяти слов. Первой группе слова предъявлялись с низкой скоростью -1 слово в 5 секунд, второй группе со средней скоростью — 1 слово в 2 секунды, и третьей группе с большой скоростью — 1 слово в секунду. Было предсказано, что показатели воспроизведения будут зависеть от скорости предъявления слов. Результаты представлены в Табл. 1.
Количество воспроизведенных слов Таблица 1
H0: Различия в объеме воспроизведения слов между группами являются не более выраженными, чем случайные различия внутрикаждой группы.
H1:Различия в объеме воспроизведения слов между группами являются более выраженными, чем случайные различия внутри каждой группы. Используя экспериментальные значения, представленные в Табл. 1, установим некоторые величины, которые будут необходимы для расчета критерия F.
Расчет основных величин для однофакторного дисперсионного анализа представим в таблице:
Последовательность операций в однофакторном дисперсионном анализе для несвязанных выборок
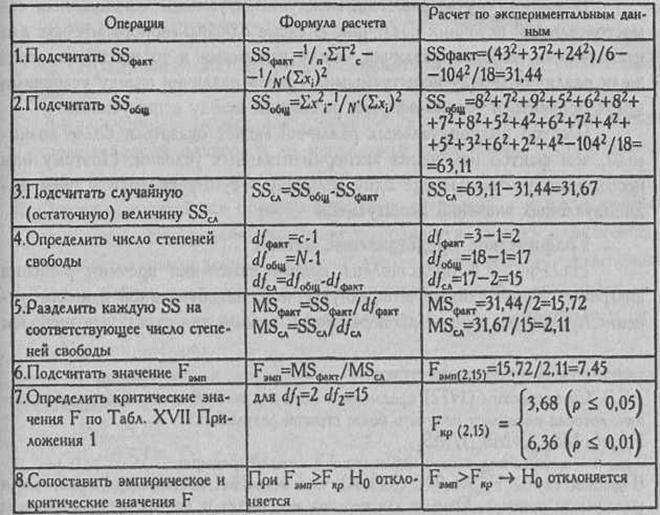
Часто встречающееся в этой и последующих таблицах обозначение SS — сокращение от «суммы квадратов» (sum of squares). Это сокращение чаще всего используется в переводных источниках.
SSфакт означает вариативность признака, обусловленную действием исследуемого фактора;
SSобщ — общую вариативность признака;
SCA -вариативность, обусловленную неучтенными факторами, «случайную» или «остаточную» вариативность.
MS — «средний квадрат», или математическое ожидание суммы квадратов, усредненная величина соответствующих SS.
df — число степеней свободы, которое при рассмотрении непараметрических критериев мы обозначили греческой буквой v.
Вывод: H0 отклоняется. Принимается H1. Различия в объеме воспроизведения слов между группами являются более выраженными, чем случайные различия внутри каждой группы (α=0,05). Итак, скорость предъявления слов влияет на объем их воспроизведения.
Пример решения задачи в Excel представлен ниже:
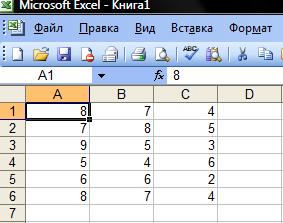
Используя команду: Сервис->Анализ данных->Однофакторный дисперсионный анализ, получим следующие результаты:
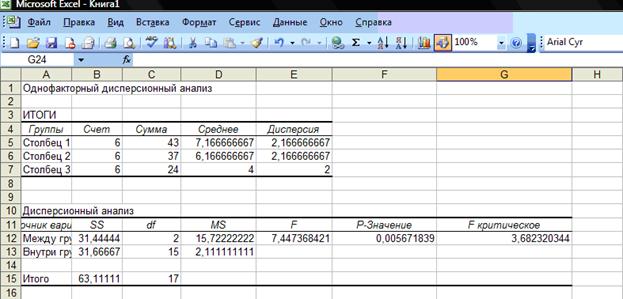
Дата добавления: 2018-06-27 ; просмотров: 4505 ; Мы поможем в написании вашей работы!
Поделиться с друзьями:
Источник: studopedia.net
Сравнение двух выборок
Основным параметрическим критерием для сравнения двух выборок является — критерий Стьюдента для независимых выборок (t-test for Independent Samples). Вариант критерия, предназначенный для сравнения средних величин выборок, ориентирован на проверку гипотезы однородности, т.е. гипотезы о том, что обе выборки извлечены из одной и той же генеральной совокупности.
Обычно при применении критерия Стьюдента предполагается, что обе выборки извлечены из генеральных совокупностей, имеющих нормальные распределения. Однако специальные исследования показали, что этот критерий, особенно при больших объемах выборок, является устойчивым к отклонениям исследуемых генеральных совокупностей от нормальных, следовательно, вообще говоря, он может применяться и к выборкам из негауссовских генеральных совокупностей, но при этом истинные значения уровня значимости и мощности критерия будут незначительно отличаться от заданных [4. C.395] и, строго говоря, должны оцениваться с помощью специальных приемов. Поэтому в «чистом виде» критерий Стьюдента все же требует нормальности распределений выборок.
Для вычисления статистики критерия существует ряд различных формул, учитывающих особенности ситуации его применения и, в частности, характер предположений о дисперсиях генеральных совокупностей, из которых извлечены выборки [1. С.169-172; 4. C.395-399; 14. С.83-85; 22. С.204-206]:
дисперсии известны и равны между собой;
дисперсии известны, но неравны между собой;
дисперсии неизвестны, но предполагается их равенство;
дисперсии неизвестны, их равенство не предполагается.
Кроме того, существуют варианты критерия для случаев равных и неравных выборок (см., напр., [1. C.170], а также для связных и несвязных выборок (вариант для связных выборок будет рассмотрен в теме 8.1). Для психологических исследований наиболее обычной является ситуация, когда дисперсии генеральных совокупностей неизвестны, но предполагается их равенство между собой; при этом исследуемые выборки могут иметь различные объемы. В этом случае статистика критерия Стьюдента вычисляется по формуле [4. С.395; 7. C.72; 22. С.205]:
, (7.1-1)
где 
— средние значения для первой и второй выборки
соответственно;
— объемы выборок;
— объединенная оценка выборочной дисперсии
которая вычисляется по следующей формуле:
, (7.1-2)
где 
и 
— оценки дисперсий для соответствующих выборок, вычисляемые, в свою очередь, по формулам:
(7.1-3)
Критерий Стьюдента обсуждается во многих работах:
его непосредственное применение в психологических исследованиях рассмотрено в [1. C.169-174; 5; 13; 29];
разнообразные примеры использования критерия приведены в [6-8; 15; 17; 18; 20];
использование критерия в статистическом пакете SPSS обсуждается в [2; 35], в пакете Statistica for Windows – в [9-11], а в пакете Stadia – в [19];
математико-статистические основания критерия рассмотрены в [4; 14; 16; 21-25; 28; 30; 31; 33].
Другим популярным параметрическим критерием является — критерий Фишера ( test), основанный на анализе дисперсий выборок. Он рассчитывается в дисперсионном анализе, который будет рассмотрен нами в теме 10.
Из непараметрических критериев для сравнения двух выборок наиболее популярен — критерий Манна-Уитни (Mann-Whitney U test), так как он имеет весьма слабые ограничения на объемы выборок (в каждой выборке должно быть не менее трех измерений), а кроме этого позволяет сравнивать между собой выборки разного объема [3. C.50]. Критерий предназначен, в частности, для проверки нулевой гипотезы о том, что средние значения двух выборок не отличаются друг от друга. Иногда эту гипотезу формулируют так: предполагается, что обе независимые выборки взяты из одной и той же генеральной совокупности.
Критерий Манна-Уитни является непараметрическим аналогом -критерия Стьюдента для независимых выборок. Он основан не на параметрах нормального распределения, а на рангах наблюдений, и, поэтому, применим к выборкам, имеющим любой характер распределения. Для применения критерия Манна-Уитни данные выборок временно объединяют и выполняют их ранжирование, а затем подсчитывают суммы рангов, полученные для данных из каждой выборки. Статистика критерия вычисляется по следующим формулам [1. С.109; 3. С.53]:
, (7.1-4)
, (7.1-5)
где 
, 
— объемы, соответственно, первой и второй выборки;
и 
— суммы рангов, соответственно, по первой и по
второй выборке;
— наибольшая из двух ранговых сумм;
— объем выборки, имеющей наибольшую сумму рангов.
Критерий Манна-Уитни рассматриваются в многочисленных литературных источниках:
методика его применения в психологических исследованиях обсуждается в [1. C.101-110; 3. С.49-55];
разнообразные примеры применения критерия приведены в [8; 15; 17; 27];
использование критерия в статистическом пакете SPSS обсуждается в [2; 35], в пакете Statistica for Windows – в [9-11], а в пакете Stadia – в [19];
математико-статистические основания критерия рассмотрены в [4; 14; 16; 21-25; 28; 31-33].
Далее рассмативаются решения задач, встречающихся при анализе психологических данных, в которых применяются критерии выявления различий в уровне признака для двух выборок.
Задача 7.1-1. Применение критерия Манна-Уитни для выявления
различий в уровне исследуемого признака
Условие: с помощью методики «Личностный дифференциал» обследованы студенты психологического факультета (выборка A) и других факультетов (выборка B). Результаты, полученные по фактору «Сила Я», приведены в табл. 7.1-1.
Найти: можно ли утверждать, что выборки отличаются друг от друга по показателю фактора «Сила Я»?
Таблица 7.1-1
Индивидуальные значения показателей фактора «Сила Я»
| № | A | B | № | A | B | № | A | B |
| 1 | 6 | 11 | — | |||||
| 2 | 7 | 12 | — | |||||
| 3 | 8 | 13 | — | |||||
| 4 | 9 | 14 | — | |||||
| 5 | 10 | 15 | — |
1. Выдвигаем гипотезы: 
– об отсутствии различий по выборкам в средних значениях показателя «Сила Я», 
– о наличии таких различий.
2. Применим для решения задачи пакет SPSS. Запускаем его и вводим исходные данные, аналогично задаче 6.2-1, используя для обеих выборок одну и ту же переменную var00001 и применяя группирующую переменную var00002, принимающую значение 1 для выборки А и значение 2 для выборки В.
3. В главном меню программы выбираем команды: Statistics (Статистики) – Nonparametric tests (Непараметрические критерии) – 2 Independent Samples… (Две независимые выборки).
4. В открывшемся окне Two-Independent-Samples Tests (Критерии для двух независимых выборок):
задаем в поле Test variable list (Список проверяемых переменных) переменную var00001,
в поле Groupping variable (Группирующая переменная) заносим переменную var00002,
флажком выбираем применяемый для проверки критерий Mann-Whitney U test (U -тест Манна-Уитни).
5. Для группирующей переменной выбираем команду Define groups (Определить группы), устанавливаем значения групп 1 и 2 и нажимаем кнопку Continue (Продолжить).
6. Выполняем саму проверку и переходим в окно SPSS Viewer (Просмотр результатов). В таблице Test statistics (Результаты теста) находим поле Mann-Whitney U, содержащее значение статистики критерия Манна-Уитни: 
= 70,0. При этом Asymp. Sig. (2-tailed) (Асимптотический двухсторонний уровень значимости) равен 0,781, что свидетельствует об отсутствии достоверных различий в средних значениях двух выборок, значит, мы не имеем оснований отвергнуть нулевую гипотезу и принимаем ее.
Ответ: статистически значимые различия между выборками отсутствуют.
Задача 7.1-2. Применение критерия Стьюдента для выявления
различий в уровне исследуемого признака
Условие: исследован уровень субъективной удовлетворенности организацией учебного процесса среди студентов первого (выборка A) и пятого (выборка B) курсов (табл. 7.1-2).
Найти: существуют ли статистически значимые различия между уровнями удовлетворенности в этих выборках?
Таблица 7.1-2
Источник: studopedia.org