Чтобы решить систему уравнений в Python, мы можем использовать функции из библиотеки NumPy .
В следующих примерах показано, как использовать NumPy для решения нескольких различных систем уравнений в Python.
Пример 1. Решение системы уравнений с двумя переменными
Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения x и y:
В следующем коде показано, как использовать NumPy для поиска значений x и y:
import numpy as np #define left-hand side of equation left_side = np.array([[5, 4], [2, 6]]) #define right-hand side of equation right_side = np.array([35, 36]) #solve for x and y np.linalg.inv (left_side). dot (right_side) array([3., 5.])
Это говорит нам о том, что значение x равно 3 , а значение y равно 5 .
Пример 2. Решение системы уравнений с тремя переменными
Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения x, y и z:
В следующем коде показано, как использовать NumPy для определения значений x, y и z:
Python. Простые алгоритмы. Решаем задачи
import numpy as np #define left-hand side of equation left_side = np.array([[4, 2, 1], [3, 5, -2], [2, 2, 4]]) #define right-hand side of equation right_side = np.array([34, 41, 30]) #solve for x, y, and z np.linalg.inv (left_side). dot (right_side) array([5., 6., 2.])
Это говорит нам о том, что значение x равно 5 , значение y равно 6 , а значение z равно 2 .
Пример 3. Решение системы уравнений с четырьмя переменными
Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения w, x, y и z:
6ш + 2х + 2у + 1з = 37
2ш + 1х + 1у + 0з = 14
3ш + 2х + 2у + 4з = 28
2ш + 0х + 5у + 5з = 28
В следующем коде показано, как использовать NumPy для определения значений w, x, y и z:
import numpy as np #define left-hand side of equation left_side = np.array([[6, 2, 2, 1], [2, 1, 1, 0], [3, 2, 2, 4], [2, 0, 5, 5]]) #define right-hand side of equation right_side = np.array([37, 14, 28, 28]) #solve for w, x, y, and z np.linalg.inv (left_side). dot (right_side) array([4., 3., 3., 1.])
Это говорит нам о том, что значение w равно 4 , x равно 3 , y равно 3 и z равно 1 .
Дополнительные ресурсы
В следующих руководствах объясняется, как решить систему уравнений с помощью другого статистического программного обеспечения:
Источник: www.codecamp.ru
Напишите программу для решения уравнения питон
В данной статье мы разберем программу на python для решения линейного уравнения Программа решает уравнение вида ax = b. Коэффициенты a и b задаются пользователем с клавиатуры. Программа находит решение и выводит его на экран. Если решений бесконечное количество или их нет, то программа оповещает об этом.
Все возможные решения линейного уравнения можно описать так
Если a = 0 и b = 0, то решений бесконечное количество.
Решение задач на Python #1
Если a = 0 и b ≠ 0, то решений нет.
Если a ≠ 0, то единственное решение будет равно b / a.
Для задания коэффициентов с клавиатуры в Python используется функция ввода вещественного числа float(input()). Подробно о вводе информации с клавиатуры в python
a = float(input(«Введите коэффициент a «))
b = float(input(«Введите коэффициент b «))
В Python, чтобы проверить равенство двух объектов, используется ==, для проверки неравенства объектов используется !=. Для проверки двух условий одновременно используется оператор and. Подробно об условиях в python
Программа на Python для решения линейного уравнения
a = float(input(«Введите коэффициент a «))
b = float(input(«Введите коэффициент b «))
if (a == 0 and b == 0):
print(«Бесконечное количество решений.»)
if (a == 0 and b != 0):
print(«Решений нет.»)
if (a != 0):
print(b/a))
Полезно почитать по теме условия в Python примеры
Пример анкеты, опроса на Python
Найти корни квадратного уравнения
Квадратное уравнение имеет вид
При его решении сначала вычисляют дискриминант по формуле
Если D > 0, то квадратное уравнение имеет два корня; если D = 0, то 1 корень; и если D
Примеры выполнения кода:
Обратим внимание, что для данной программы коэффициент a не должен быть равен нулю. Иначе в первой ветке условного оператора будет происходить попытка деления на 0.
Если a = 0 , то квадратное уравнение превращается в линейное, которое решается иным способом. Оно всегда имеет один корень.
Квадратное уравнение
Программа, позволяющая находить корни квадратного уравнения, – это один из примеров простых программ, которые можно написать на Python 3. Она хорошо подойдет для начинающих изучать этот язык программирования.
Постановка задачи
Уравнение, которое будем решать, выглядит следующим образом: a·x²+b·x+c=0. Пользователю предлагается ввести значения a, b и с в терминале. После этого программа посчитает дискриминант. На его основе найдем решения уравнения – значения x, для которых будет выполняться равенство.
Вот пример работы программы, которая будет написана.

Программа
Для решения квадратных уравнений на Python 3 напишем код, приведенный ниже. Разберем некоторые моменты, которые мы использовали в этой простой программе:
- print — эта функция выводит на экран информацию.
- input — выводит информацию и предлагает пользователю ввести данные.
- b**2 — это возведение в степень, в данном случае переменная b возводится в квадрат.
- str — эта функция приводит данные к строковому виду.
- if-elif-else — это условные операторы в языке Python. Исходя из значения discriminant мы определяем количество корней квадратного уравнения.
- discriminant ** 0.5 — с помощью такого способа извлекаем квадратный корень. В Python есть несколько способов извлечения корней, например, с помощью функции sqrt из библиотеки math. Про способы извлечения корней в Python описано в отдельной статье.
Запустим программу и введём нужные коэффициенты.
Все посчитано, найдены два корня, которые будут являться решением квадратного уравнения.
Дополнительно
Хотелось бы уделить внимание ещё одному моменту. Если дискриминант отрицательный, то действительных корней нет. Но будут комплексные корни. Если мы хотим их обрабатывать, то следует изменить конструкцию условных операторов следующим образом:
Тогда пример решения уравнения будет выглядеть следующим образом:
Как видим, получили два комплексных корня.
Этот простой код написанный на Python 3 можно для обучения программированию немного усложнить:
- Предлагать запрос в конце программы «Решить ещё одно уравнение (y/n): ». И если пользователь введет «y», то заново запросить коэффициенты. Это нужно делать в цикле. Подробнее о циклах в Python можно прочитать здесь.
- Сделать проверку корректности ввода. Ведь пользователь вместо числа может ввести какую-нибудь строку, которая не будет корректно обработана. Про проверку на число описано в отдельной статье.
Источник: al-shell.ru
Как в питоне написать программу для решения примера

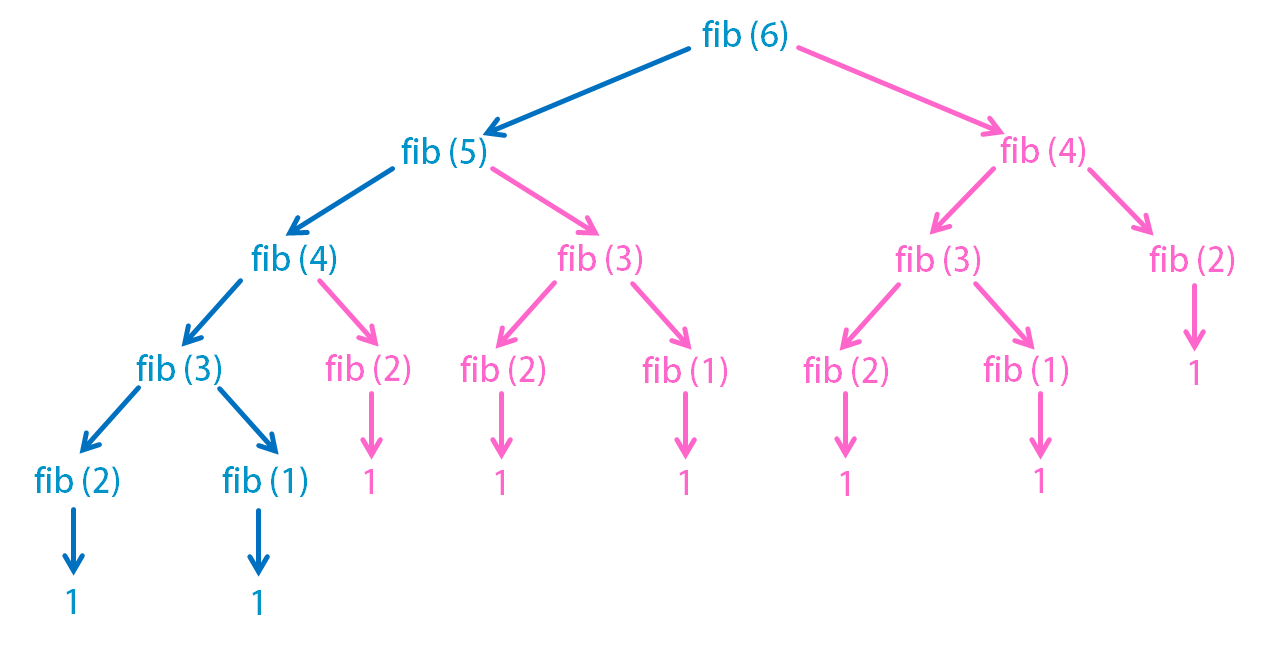
Итерацию можно назвать противоположностью рекурсии. Всегда, когда задачу можно решить итерацией (либо итерацией с использованием стека), следует делать выбор в пользу цикла for или while вместо рекурсии.
Мемоизация
Задача: лесенка представляет собой набор кубиков. В этом наборе каждый последующий ряд состоит из меньшего числа кубиков, чем предыдущий. Надо написать программу для вычисления количества лесенок, которое можно построить из n кубиков.

В решении используется рекурсивная функция, выполнение которой в интерпретаторе Python занимает столько времени, что готовое решение никогда не будет соответствовать строгим олимпиадным критериям. Для кэширования промежуточных результатов можно написать функцию мемоизации самостоятельно, а можно воспользоваться готовым, уже упомянутым выше декоратором. Сравним скорость выполнения решений с мемоизацией и без:
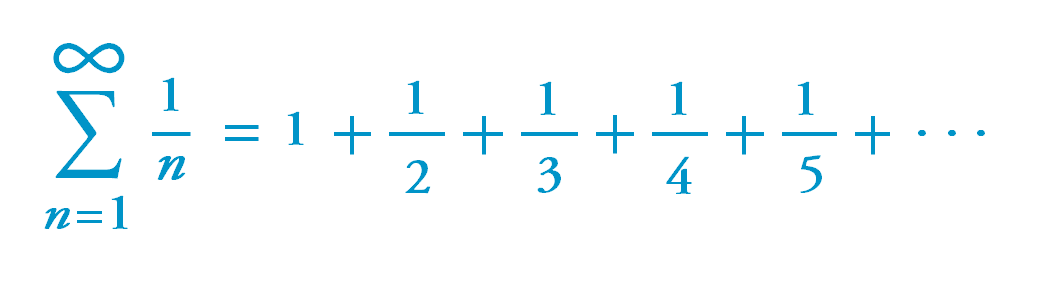
Пример ввода:
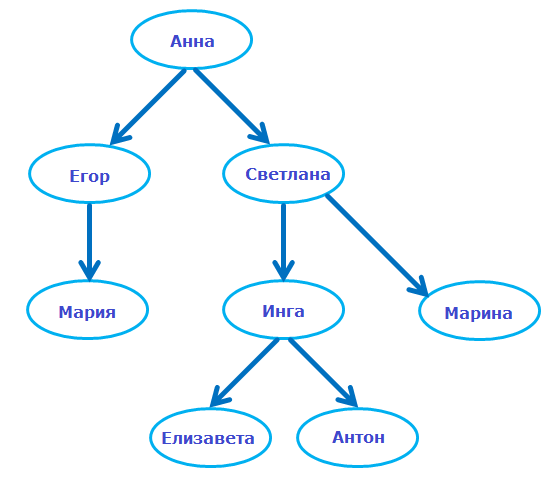
Посещаем узел Анна. Проверяем, состоит ли имя Анна из 9 букв. Посещаем узел Егор. Проверяем, состоит ли имя Егор из 9 букв. Посещаем узел Мария. Проверяем, состоит ли имя Мария из 9 букв. Посещаем узел Светлана.
Проверяем, состоит ли имя Светлана из 9 букв. Посещаем узел Инга. Проверяем, состоит ли имя Инга из 9 букв. Посещаем узел Елизавета. Проверяем, состоит ли имя Елизавета из 9 букв. Имя из 9 букв: Елизавета
root = ]>, , ]>, ]>]> def find_name(node): print(f»Посещаем узел . «) print(f»Проверяем, состоит ли имя из 9 букв. «) if len(node[‘name’]) == 9: return node[‘name’] # граничный случай if len(node[‘children’]) > 0: # рекурсивный случай for child in node[‘children’]: returnValue = find_name(child) if returnValue != ‘не найдено’: return returnValue return ‘не найдено’ # граничный случай — имен из 9 букв нет print(f»Имя из 9 букв: «)
Примечание: без рекурсии такую задачу можно решить с помощью ООП:
class Node: def __init__(self, data=None, left=None, right=None): self.data = data self.left = left self.right = right def traverse(root): if root is None: return traverse(root.left) if len(root.data) == 9: print(f’Имя найдено: ‘) return traverse(root.right) if len(root.data) == 9: print(f’Имя найдено: ‘) return if __name__ == ‘__main__’: root = Node(‘Анна’) root.left = Node(‘Егор’) root.right = Node(‘Светлана’) root.left.left = Node(‘Мария’) root.right.left = Node(‘Инга’) root.right.right = Node(‘Марина’) root.right.left.left = Node(‘Елизавета’) root.right.left.right = Node(‘Антон’) traverse(root)
Задание 9
Имеется многомерный вложенный список:
sp = [[[5, 7, 2], [4, 9, 5]], [[2, 5, 4]], [[3, 2, 1], [[5], [9, 5]]], [4, 3, 1, 2], [[4, 7, 2], [6, 4]], [[[4, 1, 6], [3, 8]], [4, 5]], [9, 1], [3, 1], [[5, 6], [[4, 2, 1], [2, 5], [[6, 8, 2, 3, 4]]]], [5, 3, 2], [2, [1], 4], [2, 5, [4, 3, 1], 6, 7, [9, 0, 5, 2, 4]], [7, 3, [4]], [4, 2, [[[5, 6, 7], 5, 7]], 1], [3, 4, 6, [6, 4, 5]], ]
Напишите рекурсивную и итеративную функции для преобразования списка в одномерный.
Ожидаемый результат:
[5, 7, 2, 4, 9, 5, 2, 5, 4, 3, 2, 1, 5, 9, 5, 4, 3, 1, 2, 4, 7, 2, 6, 4, 4, 1, 6, 3, 8, 4, 5, 9, 1, 3, 1, 5, 6, 4, 2, 1, 2, 5, 6, 8, 2, 3, 4, 5, 3, 2, 2, 1, 4, 2, 5, 4, 3, 1, 6, 7, 9, 0, 5, 2, 4, 7, 3, 4, 4, 2, 5, 6, 7, 5, 7, 1, 3, 4, 6, 6, 4, 5]
Решение 1 – рекурсивное:
def flat_list_recur(lst): if lst == []: return lst if isinstance(lst[0], list): return flat_list_recur(lst[0]) + flat_list_recur(lst[1:]) return lst[:1] + flat_list_recur(lst[1:]) sp = [[[5, 7, 2], [4, 9, 5]], [[2, 5, 4]], [[3, 2, 1], [[5], [9, 5]]], [4, 3, 1, 2], [[4, 7, 2], [6, 4]], [[[4, 1, 6], [3, 8]], [4, 5]], [9, 1], [3, 1], [[5, 6], [[4, 2, 1], [2, 5], [[6, 8, 2, 3, 4]]]], [5, 3, 2], [2, [1], 4], [2, 5, [4, 3, 1], 6, 7, [9, 0, 5, 2, 4]], [7, 3, [4]], [4, 2, [[[5, 6, 7], 5, 7]], 1], [3, 4, 6, [6, 4, 5]], ] print(flat_list_recur(sp))
Решение 2 – итеративное:
def flat_list_iter(lst): result = [] stack = [lst] while stack: current = stack.pop(-1) if isinstance(current, list): stack.extend(current) else: result.append(current) result.reverse() return result sp = [[[5, 7, 2], [4, 9, 5]], [[2, 5, 4]], [[3, 2, 1], [[5], [9, 5]]], [4, 3, 1, 2], [[4, 7, 2], [6, 4]], [[[4, 1, 6], [3, 8]], [4, 5]], [9, 1], [3, 1], [[5, 6], [[4, 2, 1], [2, 5], [[6, 8, 2, 3, 4]]]], [5, 3, 2], [2, [1], 4], [2, 5, [4, 3, 1], 6, 7, [9, 0, 5, 2, 4]], [7, 3, [4]], [4, 2, [[[5, 6, 7], 5, 7]], 1], [3, 4, 6, [6, 4, 5]], ] print(flat_list_iter(sp))
Задание 10
Реализуйте алгоритм бинарного поиска с помощью итеративной и рекурсивной функций. Число задается с помощью randrange(2000), в списке хранятся числа от 1 до 1000, т.е. не во всех случаях заданное число будет присутствовать в списке.
Пример вывода:
Число найдено: 787
Решение 1 – рекурсивное:
from random import randrange def binary_recursive(lst, start, end, num): if end >= start: mid = (end + start) // 2 if lst[mid] == num: # граничный случай — элемент находится посередине return mid elif lst[mid] > num: # рекурсивный случай — элемент находится слева return binary_recursive(lst, start, mid — 1, num) else: # рекурсивный случай — элемент находится справа return binary_recursive(lst, mid + 1, end, num) else: # граничный случай — элемент в списке не обнаружен return ‘не найдено’ sp = [i for i in range(1001)] n = randrange(2000) result = binary_recursive(sp, 0, len(sp)-1, n) if result != ‘не найдено’: print(f’Число найдено: ‘) else: print(‘Такого числа нет в списке’)
Решение 2 – итеративное:
from random import randrange def binary_iter(lst, num): start, end, mid = 0, len(lst) — 1, 0 while start num: end = mid — 1 else: return mid return ‘не найдено’ sp = [i for i in range(1001)] n = randrange(2000) result = binary_iter(sp, n) if result != ‘не найдено’: print(f’Число найдено: ‘) else: print(‘Такого числа нет в списке’)
Подведем итоги
Рекурсию стоит применять для решения задач, в которых:
- Используется древовидная структура данных.
- Нужно предусмотреть возврат к предыдущей отправной точке (например, при поиске выхода из лабиринта).
- Глубина рекурсивных вызовов находится в пределах разумного и не приведет к переполнению стека.
Во всех остальных случаях целесообразнее использовать итерацию либо итерацию и стек.
В следующей главе будем изучать функции высшего порядка и замыкания.
- Особенности, сферы применения, установка, онлайн IDE
- Все, что нужно для изучения Python с нуля – книги, сайты, каналы и курсы
- Типы данных: преобразование и базовые операции
- Методы работы со строками
- Методы работы со списками и списковыми включениями
- Методы работы со словарями и генераторами словарей
- Методы работы с кортежами
- Методы работы со множествами
- Особенности цикла for
- Условный цикл while
- Функции с позиционными и именованными аргументами
- Анонимные функции
- Рекурсивные функции
- Функции высшего порядка, замыкания и декораторы
- Методы работы с файлами и файловой системой
- Регулярные выражения
- Основы скрапинга и парсинга
- Основы ООП: инкапсуляция и наследование
- Основы ООП – абстракция и полиморфизм
- Графический интерфейс на Tkinter
- Основы разработки игр на Pygame
- Основы работы с SQLite
Источник: proglib.io