Что такое анализ?
Анализируя алгоритм, можно получить представление о том, сколько времени займет решение данной задачи при помощи данного алгоритма. Одну и ту же задачу можно решить с помощью различных алгоритмов. Анализ алгоритмов дает нам инструмент для выбора алгоритма.
Результат анализа алгоритмов — не формула для точного количества секунд или компьютерных циклов, которые потребует конкретный алгоритм. Нужно понимать, что разница между алгоритмом, который делает N + 5 операций, и тем, который делает N + 250 операций, становится незаметной, как только N становится очень большим.
Классы входных данных
При анализе алгоритма выбор входных данных может существенно повлиять на его выполнение. Скажем, некоторые алгоритмы сортировки могут работать очень быстро, если входной список уже отсортирован, тогда как другие алгоритмы покажут весьма скромный результат на таком списке. А вот на случайном списке результат может оказаться противоположным.
Поэтому не будем ограничиваться анализом поведения алгоритмов на одном входном наборе данных. Практически нужно искать такие данные, которые обеспечивают как самое быстрое, так и самое медленное выполнение алгоритма. Кроме того, полезно оценивать и среднюю эффективность алгоритма на всех возможных наборах данных.
Оценка сложности алгоритмов | О большое | Алгоритмы и структуры данных
Наилучший случай
Время выполнения алгоритма в наилучшем случае очень часто оказывается маленьким или просто постоянным, поэтому подобный анализ проводится редко.
Наихудший случай
Анализ наихудшего случая чрезвычайно важен, поскольку он позволяет представить максимальное время работы алгоритма. При анализе наихудшего случая необходимо найти входные данные, на которых алгоритм будет выполнять больше всего работы.
Средний случай

Анализ среднего случая является самым сложным, поскольку он требует учета множества разнообразных деталей. В основе анализа лежит определение различных групп, на которые следует разбить возможные входные наборы данных. На втором шаге определяется вероятность, с которой входной набор данных принадлежит каждой группе. На третьем шаге подсчитывается время работы алгоритма на данных из каждой группы. Время работы алгоритма на всех входных данных одной группы должно быть одинаковым, в противном случае группу следует подразбить. Среднее время работы вычисляется по формуле
где через n обозначен размер входных данных, через m — число групп. через pi — вероятность того, что входные данные принадлежат группе с номером i, а через ti — время, необходимое алгоритму для обработки данных из группы с номером i.

В большинстве случаев мы будем предполагать, что вероятности попадания входных данных в каждую из групп одинаковы. Другими словами, если групп пять, то вероятность попасть в первую группу такая же, как вероятность попасть во вторую, и т.д., то есть вероятность
ВСЯ СЛОЖНОСТЬ АЛГОРИТМОВ ЗА 11 МИНУТ | ОСНОВЫ ПРОГРАММИРОВАНИЯ
попасть в каждую группу равна 0.2. В этом случае среднее время работы можно либо оценить по предыдущей формуле, либо воспользоваться эквивалентной ей формулой

Нижние границы. Дерево решений.
Алгоритм является оптимальным, если любой любой другой алгоритм, решающий данную задачу, работает не быстрее данного. Как узнать оптимальность алгоритма? Для этого мы должны знать минимальное количество операций, необходимое для решения поставленной задачи, которое называется нижней границей. Но для этого нам нужно изучать именно ЗАДАЧУ, а не конкретный алгоритм!
Как пример, рассмотрим анализ процесса сортировки списка из 3 чисел, воспользовавшись бинарным деревом. Такое дерево называется деревом решений.
Самый длинный путь в данном дереве соответствует наихудшему случаю и наоборот, кратчайший — наилучшему. Средний случай описывается частным от деления числа ребер в дереве на число листов.
Для перестановки 2-х элементов мы имеем 1лист, для N эл-тов, по правилам комбинаторики, N! листов. Число листов на уровне K равно 2k-1, поэтому в нашем дереве решений буде L -уровней, где L — наименьшее целое число, для которого N! ≤ 2L-1. Логарифмируя, получим 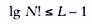
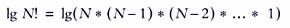

В конечном итоге, получаем: 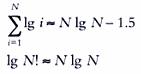
Вот мы и узнали, что любой алгоритм сортировки, порядка О(NlgN) является наилучшим и его можно считать оптимальным. Более того, из этого исследования вытекает, что алгоритм, решающий задачу сортировки быстрее О(NlgN) операций, не может работать правильно!
Источник: habr.com
Как узнать алгоритм программы

Комментарии
Популярные По порядку
Не удалось загрузить комментарии.
ЛУЧШИЕ СТАТЬИ ПО ТЕМЕ
10 структур данных, которые вы должны знать (+видео и задания)
Бо Карнс – разработчик и преподаватель расскажет о наиболее часто используемых и общих структурах данных. Специально для вас мы перевели его статью.
Какие алгоритмы нужно знать, чтобы стать хорошим программистом?
Данная статья содержит не только самые распространенные алгоритмы и структуры данных, но и более сложные вещи, о которых вы могли не знать. Читаем и узнаем!
Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы
В этой подборке представлен список книг, веб-сайтов и онлайн-курсов, дающих понимание как простых, так и продвинутых алгоритмов.
Источник: proglib.io
Алгоритм Дейкстры нахождения кратчайшего пути
Рассмотрим пример нахождение кратчайшего пути. Дана сеть автомобильных дорог, соединяющих области города. Некоторые дороги односторонние. Найти кратчайшие пути от центра города до каждого города области.
Для решения указанной задачи можно использовать алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Работает только для графов без рёбер отрицательного веса.
Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

Кружками обозначены вершины, линиями – пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначен их вес – длина пути. Рядом с каждой вершиной красным обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.
Инициализация

Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.
Первый шаг
Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим соседей вершины по очереди.

Первый сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1 (значению её метки) и длины ребра, идущего из 1-й во 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2 (10000), поэтому новая метка 2-й вершины равна 7.
Аналогично находим длины пути для всех других соседей (вершины 3 и 6).
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вершина 1 отмечается как посещенная.
Второй шаг
Шаг 1 алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.

Вершина 1 уже посещена. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а 9 < 17, поэтому метка не меняется.
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна 22 (7 + 15 = 22). Поскольку 22
Все соседи вершины 2 просмотрены, помечаем её как посещенную.
Третий шаг

Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим следующие результаты.
Четвертый шаг

Пятый шаг

Шестой шаг

Таким образом, кратчайшим путем из вершины 1 в вершину 5 будет путь через вершины 1 — 3 — 6 — 5, поскольку таким путем мы набираем минимальный вес, равный 20.
Займемся выводом кратчайшего пути. Мы знаем длину пути для каждой вершины, и теперь будем рассматривать вершины с конца. Рассматриваем конечную вершину (в данном случае — вершина 5), и для всех вершин, с которой она связана, находим длину пути, вычитая вес соответствующего ребра из длины пути конечной вершины.
Так, вершина 5 имеет длину пути 20. Она связана с вершинами 6 и 4.
Для вершины 6 получим вес 20 — 9 = 11 (совпал).
Для вершины 4 получим вес 20 — 6 = 14 (не совпал).
Если в результате мы получим значение, которое совпадает с длиной пути рассматриваемой вершины (в данном случае — вершина 6), то именно из нее был осуществлен переход в конечную вершину. Отмечаем эту вершину на искомом пути.
Далее определяем ребро, через которое мы попали в вершину 6. И так пока не дойдем до начала.
Если в результате такого обхода у нас на каком-то шаге совпадут значения для нескольких вершин, то можно взять любую из них — несколько путей будут иметь одинаковую длину.
Реализация алгоритма Дейкстры
Для хранения весов графа используется квадратная матрица. В заголовках строк и столбцов находятся вершины графа. А веса дуг графа размещаются во внутренних ячейках таблицы. Граф не содержит петель, поэтому на главной диагонали матрицы содержатся нулевые значения.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 7 | 9 | 14 | |||
| 2 | 7 | 10 | 15 | |||
| 3 | 9 | 10 | 11 | 2 | ||
| 4 | 15 | 11 | 6 | |||
| 5 | 6 | 9 | ||||
| 6 | 14 | 2 | 9 |
Реализация на C++
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#define SIZE 6
int main()
int a[SIZE][SIZE]; // матрица связей
int d[SIZE]; // минимальное расстояние
int v[SIZE]; // посещенные вершины
int temp, minindex, min;
int begin_index = 0;
system( «chcp 1251» );
system( «cls» );
// Инициализация матрицы связей
for ( int i = 0; i a[i][i] = 0;
for ( int j = i + 1; j
scanf( «%d» ,
a[i][j] = temp;
a[j][i] = temp;
>
>
// Вывод матрицы связей
for ( int i = 0; i for ( int j = 0; j printf( «%5d » , a[i][j]);
printf( «n» );
>
//Инициализация вершин и расстояний
for ( int i = 0; i d[i] = 10000;
v[i] = 1;
>
d[begin_index] = 0;
// Шаг алгоритма
do minindex = 10000;
min = 10000;
for ( int i = 0; i < // Если вершину ещё не обошли и вес меньше min
if ((v[i] == 1) (d[i]
< // Переприсваиваем значения
min = d[i];
minindex = i;
>
>
// Добавляем найденный минимальный вес
// к текущему весу вершины
// и сравниваем с текущим минимальным весом вершины
if (minindex != 10000)
for ( int i = 0; i if (a[minindex][i] > 0)
temp = min + a[minindex][i];
if (temp < d[i])
d[i] = temp;
>
>
>
v[minindex] = 0;
>
> while (minindex < 10000);
// Вывод кратчайших расстояний до вершин
printf( «nКратчайшие расстояния до вершин: n» );
for ( int i = 0; i printf( «%5d » , d[i]);
// Восстановление пути
int ver[SIZE]; // массив посещенных вершин
int end = 4; // индекс конечной вершины = 5 — 1
ver[0] = end + 1; // начальный элемент — конечная вершина
int k = 1; // индекс предыдущей вершины
int weight = d[end]; // вес конечной вершины
while (end != begin_index) // пока не дошли до начальной вершины
for ( int i = 0; i if (a[i][end] != 0) // если связь есть
int temp = weight — a[i][end]; // определяем вес пути из предыдущей вершины
if (temp == d[i]) // если вес совпал с рассчитанным
< // значит из этой вершины и был переход
weight = temp; // сохраняем новый вес
end = i; // сохраняем предыдущую вершину
ver[k] = i + 1; // и записываем ее в массив
k++;
>
>
>
// Вывод пути (начальная вершина оказалась в конце массива из k элементов)
printf( «nВывод кратчайшего путиn» );
for ( int i = k — 1; i >= 0; i—)
printf( «%3d » , ver[i]);
getchar(); getchar();
return 0;
>

Результат выполнения
Комментариев к записи: 179
Источник: prog-cpp.ru