Как создать программу с нейросетью

В этой статье поговорим о том, как создавать нейросети и в качестве примера рассмотрим, как сделать нейронную сеть прямого распространения с нуля.

Только ленивый не слышал сегодня о существовании и разработке нейронных сетей и такой сфере, как машинное обучение . Для некоторых создание нейросети кажется чем-то очень запутанным, однако на самом деле они создаются не так уж и сложно. Как же их делают?

Давайте попробуем самостоятельно создать нейросеть прямого распространения, которую еще называют многослойным перцептроном . В процессе работы будем использовать лишь циклы, массивы и условные операторы. Что означает этот набор данных? Только то, что нам подойдет любой язык программирования, поддерживающий вышеперечисленные возможности. Если же у языка есть библиотеки для векторных и матричных вычислений (вспоминаем NumPy в Python), то реализация с их помощью займет совсем немного времени. Но мы не ищем легких путей и воспользуемся C#, причем полученный код по своей сути будет почти аналогичным и для прочих языков программирования.

Полезная Нейросеть для Удаленщика. ИИ захватывает МИР на уровне реального времени в (AI) REAL LIFE

Что же такое нейронная сеть?

Под искусственной нейронной сетью (ИНС) понимают математическую модель (включая ее программное либо аппаратное воплощение), которая построена и работает по принципу функционирования биологических нейросетей — речь идет о нейронных сетях нервных клеток живых организмов.

Говоря проще, ИНС можно назвать неким «черным ящиком», превращающим входные данные в выходные данные. Если же посмотреть на это с точки зрения математики, то речь идет о том, чтобы отобразить пространство входных X-признаков в пространство выходных Y-признаков: X → Y. Таким образом, нам надо найти некую F-функцию, которая сможет выполнить данное преобразование. На первом этапе этой информации достаточно в качестве основы.

Какую роль играет искусственный нейрон?

В нашей статье мы не будем вдаваться в лирику и рассказывать об устройстве биологического нейрона в контексте его связи с искусственной моделью. Лучше сразу перейдем к делу.

Искусственный нейрон представляет собой взвешенную сумму векторных значений входных элементов. Эта сумма передается на нелинейную функцию активации f:

Но об активации поговорим после, т. к. сейчас стоит задача узнать, каким образом вместо одного выходного значения можно получить n-значений.

Нейрослой

Один нейрон может превратить в одну точку входной вектор, но по условию мы желаем получить несколько точек, т. к. выходное Y способно иметь произвольную размерность, которая определяется лишь ситуацией (один выход для XOR, десять выходов, чтобы определить принадлежность к одному из десяти классов, и так далее). Каким же образом получить n точек? На деле все просто: для получения n выходных значений, надо задействовать не один нейрон, а n. В результате для каждого элемента выходного Y будет использовано n разных взвешенных сумм от X. В итоге мы придем к следующему соотношению:

Давайте внимательно посмотрим на него. Вышенаписанная формула — это не что иное, как определение умножения матрицы на вектор. И в самом деле, если мы возьмем матрицу W размера n на m и выполним ее умножение на X размерности m, то мы получим другое векторное значение n-размерности, то есть как раз то, что надо.

Топ-3 нейросети #айти #нейросети

Таким образом, мы можем записать похожее выражение в более удобной матричной форме:

Но полученный вектор представляет собой неактивированное состояние (промежуточное, невыходное) всех нейронов, а для того, чтобы нам получить выходное значение, нужно каждое неактивированное значение подать на вход вышеупомянутой функции активации. Итогом ее применения и станет выходное значение слоя.

Ниже показан пример нейронной сети, имеющей 2 входа, 5 нейронов и 1 выход:

Последовательность нейрослоев часто применяют для более глубокого обучения нейронной сети и большей формализации имеющихся данных. Именно поэтому, чтобы получить итоговый выходной вектор, нужно проделать вышеописанную операцию пару раз подряд по направлению от одного слоя к другому. В результате для 1-го слоя входным вектором будет являться X, а для последующих входом будет выход предыдущего слоя. То есть нейронная сеть может выглядеть следующим образом:

Функция активации

Речь идет о функции, добавляющей в нейронную сеть нелинейность. В результате нейроны смогут относительно точно сымитировать любую функцию. Широко распространены следующие функции активации:

Каждая из них имеет свои особенности.

Пишем код

Теперь мы знаем достаточно, чтобы создать простую нейронную сеть. Чтобы сделать то, что задумали, нам потребуются:

1. Вектор.
2. Матрица (каждый слой включает в себя матрицу весовых коэффициентов).
3. Нейронная сеть.

Начнем с вектора . Создавать его можно:

• из количества элементов;
• из перечисления вещественных чисел.

Также мы можем получать и менять значения по индексу i.

Теперь очередь матрицы . Ее можно создавать из числа строк и столбцов, а также генератора случайных чисел, причем есть возможность получать и менять значения по индексам i и j.

А вот и сама нейронная сеть:

Как будем обучать?

Пусть у нас уже есть нейронная сеть, но ведь ее ответы являются случайными, то есть наша нейросеть не обучена. Сейчас она способна лишь по входному вектору input выдавать случайный ответ, но нам нужны ответы, которые удовлетворяют конкретной поставленной задаче. Дабы этого достичь, сеть надо обучить. Здесь потребуется база тренировочных примеров и множество пар X — Y, на которых и будет происходить обучение, причем с использованием известного алгоритма обратного распространения ошибки .

Некоторые особенности работы этого алгоритма:

• на вход сети подается обучающий пример (1 входной вектор);
• сигнал распространяется по нейросети вперед (получаем выход сети);
• вычисляется ошибка (это разница между получившимся и ожидаемым векторами);
• ошибка распространяется на предыдущие слои;
• происходит обновление весовых коэффициентов в целях уменьшения ошибки.

Вот как выглядит алгоритм обучения:

Переходим к обучению

Для обратного распространения ошибки нужно знать значения выходов и входов, а также значения производных функции активации нейросети, причем послойно, следовательно, нужно создать структуру LayerT, где будут три векторных значения:

• x — вход слоя,
• z — выход,
• df — производная функции активации.

Для каждого слоя нам потребуются векторы дельт, в результате чего надо будет добавить в класс еще и их. В итоге класс будет выглядеть следующим образом:

Несколько слов об обратном распространении ошибки

В качестве функции оценки нейросети E(W) мы берем среднее квадратичное отклонение:

Источник: dzen.ru

Нейросеть с нуля своими руками. Часть 1. Теория

Здравствуйте. Меня зовут Андрей, я frontend-разработчик и я хочу поговорить с вами на такую тему как нейросети. Дело в том, что ML технологии все глубже проникают в нашу жизнь, и о нейросетях сказано и написано уже очень много, но когда я захотел разобраться в этом вопросе, я понял что в интернете есть множество гайдов о том как создать нейросеть и выглядят они примерно следующим образом:

1. Берем Tensorflow
2. Создаем нейросеть

Более подробная информация разбросана кусками по всему интернету. Поэтому я постарался собрать ее воедино и изложить в этой статье. Сразу оговорюсь, что я не являюсь специалистом в области ML или биологии, поэтому местами могу быть не точным. В таком случае буду рад вашим комментариям.

Пока я писал эту статью я понял, что у меня получается довольно объемный лонгрид, поэтому решил разбить ее на несколько частей. В первой части мы поговорим о теории, во второй напишем собственную нейросеть с нуля без использования каких-либо библиотек, в третьей попробуем применить ее на практике.

Так как это моя первая публикация, появляться они будут по мере прохождения модерации, после чего я добавлю ссылки на все части. Итак, приступим.

Для чего нужны нейросети

Нейросети встречаются везде. Основная их функция — это управление различными частями организма в зависимости от изменения окружающих условий. В качестве примера можно рассмотреть механизм сужения и расширения зрачка в зависимости от уровня освещения.

В нашем глазу есть сенсоры, которые улавливают количество света попадающего через зрачок на заднюю поверхность глаза. Они преобразуют эту информацию в электрические импульсы и передают на прикрепленные к ним нервные окончания. Далее это сигнал проходит по всей нейронной сети, которая принимает решение о том, не опасно ли такое количество света для глаза, достаточно ли оно для того, чтобы четко распознавать визуальную информацию, и нужно ли, исходя из этих факторов, уменьшить или увеличить количество света.

На выходе этой сети находятся мышцы, отвечающие за расширение или сужение зрачка, и приводят эти механизмы в действие в зависимости от сигнала, полученного из нейросети. И таких механизмов огромное количество в теле любого живого существа, обладающего нервной системой.

Устройство нейрона

Нейросети встречаются в природе в виде нервной системы того или иного существа. В зависимости от выполняемой функции и расположения, они делятся на различные отделы и органы, такие как головной мозг, спинной мозг, различные проводящие структуры. Но все их объединяет одно — они состоят из связанных между собой структурно-функциональных единиц — клеток нейронов.

Нейрон условно можно разделить на три части: тело нейрона, и его отростки — дендриты и аксон.

Дендриты нейрона создают дендритное дерево, размер которого зависит от числа контактов с другими нейронами. Это своего рода входные каналы нервной клетки. Именно с их помощью нейрон получает сигналы от других нейронов.

Тело нейрона в природе, достаточно сложная штука, но именно в нем все сигналы, поступившие через дендриты объединяются, обрабатываются, и принимается решение о том передавать ли сигнал далее, и какой силы он должен быть.

Аксон — это выходной интерфейс нейрона. Он крепится так называемыми синапсами к дендриту другого нейрона, и по нему сигнал, выходящий из тела нейрона, поступает к следующей клетке нашей нейросети.

Нейросети в IT

Что же, раз механизм нам понятен, почему бы нам не попробовать воспроизвести его с помощью информационных технологий?

Итак, у нас есть входной слои нейронов, которые, по сути, являются сенсорами нашей системы. Они нужны для того, чтобы получить информацию из окружающей среды и передать ее дальше в нейросеть.

Также у нас есть несколько слоев нейронов, каждый из которых получает информацию от всех нейронов предыдущего слоя, каким-то образом ее обрабатывают, и передают на следующий слой.

И, наконец, у нас есть выходные нейроны. Исходя из сигналов, поступающих от них, мы можем судить о принятом нейросетью решении.

Такой простейший вариант нейронной сети называется перцептрон, и именно его мы с вами и попробуем воссоздать.

Все нейроны по сути одинаковы, и принимают решение о том, какой силы сигнал передать далее с помощью одного и того же алгоритма. Это алгоритм называется активационной функцией. На вход она получает сумму значений входных сигналов, а на выход передает значение выходного сигнала.

Но в таком случае, получается, что все нейроны любого слоя будут получать одинаковый сигнал, и отдавать одинаковое значение. Таким образом мы могли бы заменить всю нашу сеть на один нейрон. Чтобы устранить эту проблему, мы присвоим входу каждого нейрона определенный вес. Этот вес будет обозначать насколько важен для каждого конкретного нейрона сигнал, получаемый от другого нейрона. И тут мы подходим к самому интересному.

Обучение нейронной сети — это процесс подбора входных весов для каждого нейрона таким образом, чтобы на выходе получить сигнал максимально соответствующий ожиданиям.

То есть мы подаем на вход нейросети определенные данные, для которых мы знаем, каким должен быть результат. Далее мы сравниваем результат, который нам выдала нейросеть с ожидаемым результатом, вычисляем ошибку, и корректируем веса нейронов таким образом, чтобы эту ошибку минимизировать. И повторяем это действие большое количество раз для большого количества наборов входных и выходных данных, чтобы сеть поняла какие сигналы на каком нейроне ей важны больше, а какие меньше. Чем больше и разнообразнее будет набор данных для обучения, тем лучше нейросеть сможет обучиться и впоследствии давать правильный результат. Этот процесс называется обучением с учителем.

Добавим немного математики.

В качестве активационной функции нейрона может выступать любая функция, существующая на всем отрезке значений, получающихся на выходе нейрона и входных данных. Для нашего примера мы возьмем сигмоиду. Она существует на отрезке от минус бесконечности до бесконечности, плавно меняется от 0 до 1 и имеет значение 0,5 в точке 0. Идеальный кандидат. Выглядит она следующим образом:

Таким образом наш нейрон сможет принимать любую сумму значений всех входящих сигналов и на выходе будет выдавать значение от 0 до 1. Это хорошо подходит для принятия бинарных решений, и мы условимся, что если число на выходе нейросети > 0.5, мы будем расценивать его как истину, иначе — как ложь.

Итак, давайте рассмотрим пример с топологией сети рассмотренной выше. У нас есть три входных нейрона со значениями ИСТИНА, ЛОЖЬ и ИСТИНА соответственно, два нейрона в среднем слое нейросети (эти слои также называют скрытыми), и один выходной нейрон, который сообщит нам о решении, принятом нейросетью. Так как наша сеть еще не обучена, поэтому значения весов на входах нейронов мы возьмем случайными в диапазоне от -0,5 до 0,5.

Таким образом сумма входных значений первого нейрона скрытого слоя будет равна

1 * 0,43 + 0 * 0,18 + 1 * -0,21 = 0,22

Передав это значение в активационную функцию, мы получим значение, которое наш нейрон передаст далее по сети в следующий слой.

sigmoid(0,22) = 1 / (1 + e^-0,22) = 0,55

Аналогичные операции произведём для второго нейрона скрытого слоя и получим значение 0,60.

И, наконец, повторим эти операции для единственного нейрона в выходном слое нашей нейросети и получим значение 0,60, что мы условились считать как истину.

Пока что это абсолютно случайное значение, так как веса мы выбирали случайно. Но, предположим, что мы знаем ожидаемое значение для такого набора входных данных и наша сеть ошиблась. В таком случае нам нужно вычислить ошибку и изменить параметры весов, таким образом немного обучив нашу нейросеть.

Первым делом рассчитаем ошибку на выходе сети. Делается это довольно просто, нам просто нужно получить разницу полученного значения и ожидаемого.

error = 0.60 — 0 = 0.60

Чтобы узнать насколько нам надо изменить веса нашего нейрона, нам нужно величину ошибки умножить на производную от нашей активационной функции в этой точке. К счастью, производная от сигмоиды довольно проста.

Таким образом наша дельта весов будет равна

delta = 0.60 * (1 — 0.60) = 0.24

Новый вес для входа нейрона рассчитывается по формуле

weight = weight — output * delta * learning rate

Где weight — текущий вес, output — значение на выходе предыдущего нейрона, delta — дельта весов, которую мы рассчитали ранее и learning rate — значение, подбираемое экспериментально, от которого зависит скорость обучения нейросети. Если оно будет слишком маленьким — нейросеть будет более чувствительна к деталям, но будет обучаться слишком медленно и наоборот. Для примера возьмем learning rate равным 0,3. Итак новый вес для первого входа выходного нейрона будет равен:

w = 0,22 — 0,55 * 0,24 * 0,3 = 0,18

Аналогичным образом рассчитаем новый вес для второго входа выходного нейрона:

w = 0.47 — 0.60 * 0.24 * 0.3 = 0.43

Итак, мы скорректировали веса для входов выходного нейрона, но чтобы рассчитать остальные, нам нужно знать ошибку для каждого из нейронов нашей нейросети. Это делается не так очевидно как для выходного нейрона, но тоже довольно просто. Чтобы получить ошибку каждого нейрона нам нужно новый вес нейронной связи умножить на дельту. Таким образом ошибка первого нейрона скрытого слоя равна:

error = 0.18 * 0.24 = 0.04

Теперь, зная ошибку для нейрона, мы можем произвести все те же самые операции, что провели ранее, и скорректировать его веса. Этот процесс называется обратным распространением ошибки.

Итак, мы знаем как работает нейрон, что такое нейронные связи в нейросети и как происходит процесс обучения. Этих знаний достаточно чтобы применить их на практике и написать простейшую нейросеть, чем мы и займемся в следующей части статьи.

• JavaScript
• Программирование
• Научно-популярное

Источник: habr.com

Как создать и обучить нейросеть?

В этой статье поговорим о том, как создавать нейросети и в качестве примера рассмотрим, как сделать нейронную сеть прямого распространения с нуля. Для реализации поставленной задачи воспользуемся языком программирования C#.

Только ленивый не слышал сегодня о существовании и разработке нейронных сетей и такой сфере, как машинное обучение. Для некоторых создание нейросети кажется чем-то очень запутанным, однако на самом деле они создаются не так уж и сложно. Как же их делают?

Давайте попробуем самостоятельно создать нейросеть прямого распространения, которую еще называют многослойным перцептроном. В процессе работы будем использовать лишь циклы, массивы и условные операторы. Что означает этот набор данных? Только то, что нам подойдет любой язык программирования, поддерживающий вышеперечисленные возможности.

Если же у языка есть библиотеки для векторных и матричных вычислений (вспоминаем NumPy в Python), то реализация с их помощью займет совсем немного времени. Но мы не ищем легких путей и воспользуемся C#, причем полученный код по своей сути будет почти аналогичным и для прочих языков программирования.

Что же такое нейронная сеть?

Под искусственной нейронной сетью (ИНС) понимают математическую модель (включая ее программное либо аппаратное воплощение), которая построена и работает по принципу функционирования биологических нейросетей — речь идет о нейронных сетях нервных клеток живых организмов.

Говоря проще, ИНС можно назвать неким «черным ящиком», превращающим входные данные в выходные данные. Если же посмотреть на это с точки зрения математики, то речь идет о том, чтобы отобразить пространство входных X-признаков в пространство выходных Y-признаков: X → Y. Таким образом, нам надо найти некую F-функцию, которая сможет выполнить данное преобразование. На первом этапе этой информации достаточно в качестве основы.

Какую роль играет искусственный нейрон?

В нашей статье мы не будем вдаваться в лирику и рассказывать об устройстве биологического нейрона в контексте его связи с искусственной моделью. Лучше сразу перейдем к делу.

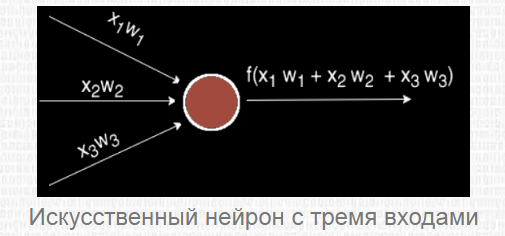
Искусственный нейрон представляет собой взвешенную сумму векторных значений входных элементов. Эта сумма передается на нелинейную функцию активации f:

Но об активации поговорим после, т. к. сейчас стоит задача узнать, каким образом вместо одного выходного значения можно получить n-значений.

Нейрослой

Один нейрон может превратить в одну точку входной вектор, но по условию мы желаем получить несколько точек, т. к. выходное Y способно иметь произвольную размерность, которая определяется лишь ситуацией (один выход для XOR, десять выходов, чтобы определить принадлежность к одному из десяти классов, и так далее). Каким же образом получить n точек? На деле все просто: для получения n выходных значений, надо задействовать не один нейрон, а n. В результате для каждого элемента выходного Y будет использовано n разных взвешенных сумм от X. В итоге мы придем к следующему соотношению:

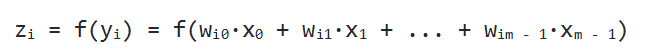
Давайте внимательно посмотрим на него. Вышенаписанная формула — это не что иное, как определение умножения матрицы на вектор. И в самом деле, если мы возьмем матрицу W размера n на m и выполним ее умножение на X размерности m, то мы получим другое векторное значение n-размерности, то есть как раз то, что надо.

Таким образом, мы можем записать похожее выражение в более удобной матричной форме:

Но полученный вектор представляет собой неактивированное состояние (промежуточное, невыходное) всех нейронов, а для того, чтобы нам получить выходное значение, нужно каждое неактивированное значение подать на вход вышеупомянутой функции активации. Итогом ее применения и станет выходное значение слоя.

Ниже показан пример нейронной сети, имеющей 2 входа, 5 нейронов и 1 выход:

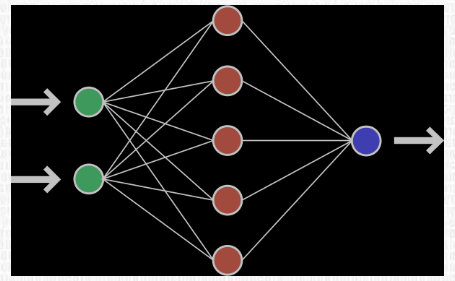
Последовательность нейрослоев часто применяют для более глубокого обучения нейронной сети и большей формализации имеющихся данных. Именно поэтому, чтобы получить итоговый выходной вектор, нужно проделать вышеописанную операцию пару раз подряд по направлению от одного слоя к другому. В результате для 1-го слоя входным вектором будет являться X, а для последующих входом будет выход предыдущего слоя. То есть нейронная сеть может выглядеть следующим образом:

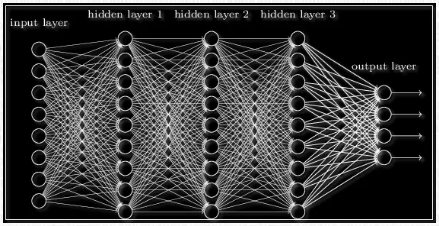
Функция активации

Речь идет о функции, добавляющей в нейронную сеть нелинейность. В результате нейроны смогут относительно точно сымитировать любую функцию. Широко распространены следующие функции активации:

Каждая из них имеет свои особенности.

Пишем код

Теперь мы знаем достаточно, чтобы создать простую нейронную сеть. Чтобы сделать то, что задумали, нам потребуются:

1. Вектор.
2. Матрица (каждый слой включает в себя матрицу весовых коэффициентов).
3. Нейронная сеть.

Начнем с вектора. Создавать его можно:

• из количества элементов;
• из перечисления вещественных чисел.

Также мы можем получать и менять значения по индексу i.

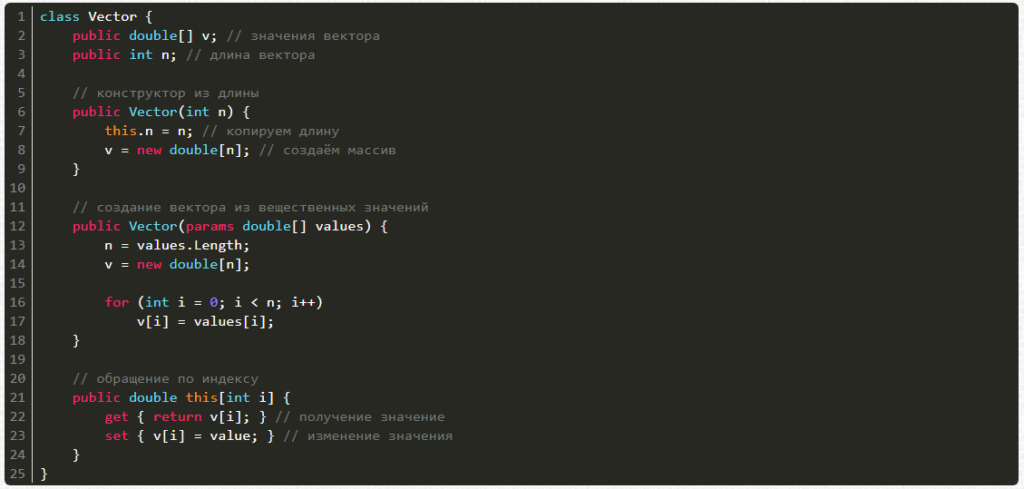
Теперь очередь матрицы. Ее можно создавать из числа строк и столбцов, а также генератора случайных чисел, причем есть возможность получать и менять значения по индексам i и j.

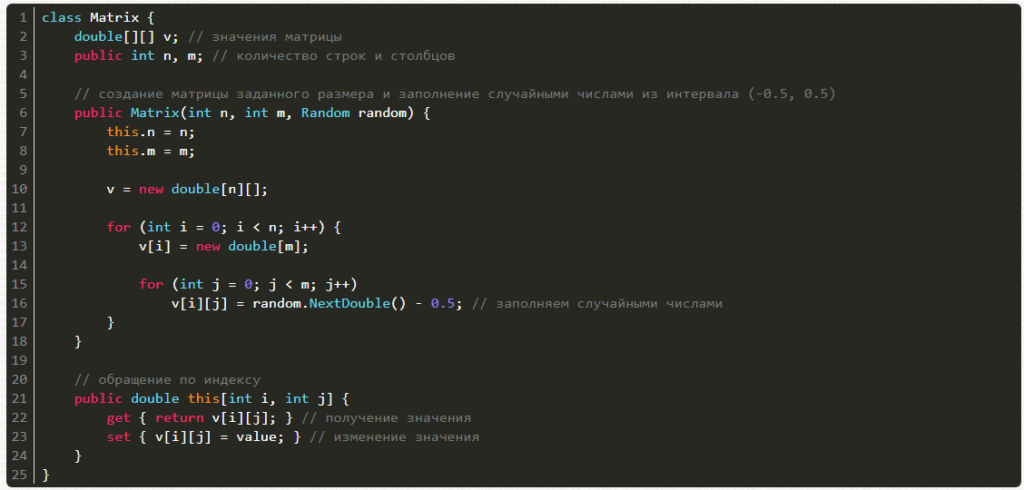
А вот и сама нейронная сеть:

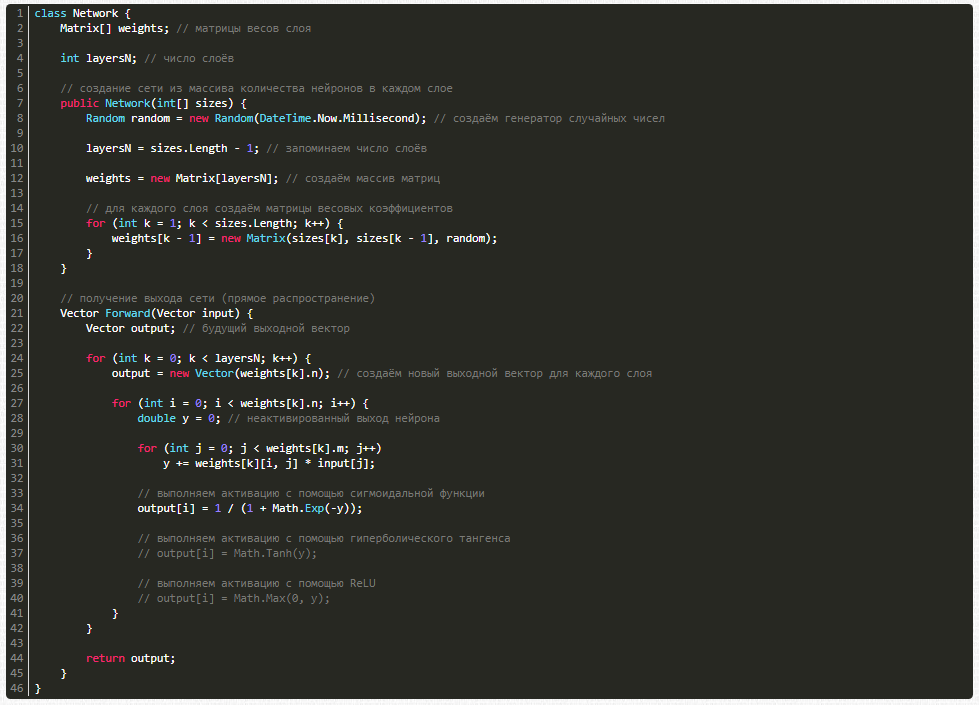
Как будем обучать?

Пусть у нас уже есть нейронная сеть, но ведь ее ответы являются случайными, то есть наша нейросеть не обучена. Сейчас она способна лишь по входному вектору input выдавать случайный ответ, но нам нужны ответы, которые удовлетворяют конкретной поставленной задаче. Дабы этого достичь, сеть надо обучить. Здесь потребуется база тренировочных примеров и множество пар X — Y, на которых и будет происходить обучение, причем с использованием известного алгоритма обратного распространения ошибки.

Некоторые особенности работы этого алгоритма:

• на вход сети подается обучающий пример (1 входной вектор);
• сигнал распространяется по нейросети вперед (получаем выход сети);
• вычисляется ошибка (это разница между получившимся и ожидаемым векторами);
• ошибка распространяется на предыдущие слои;
• происходит обновление весовых коэффициентов в целях уменьшения ошибки.

Вот как выглядит алгоритм обучения:

Переходим к обучению

Для обратного распространения ошибки нужно знать значения выходов и входов, а также значения производных функции активации нейросети, причем послойно, следовательно, нужно создать структуру LayerT, где будут три векторных значения:

• x — вход слоя,
• z — выход,
• df — производная функции активации.

Для каждого слоя нам потребуются векторы дельт, в результате чего надо будет добавить в класс еще и их. В итоге класс будет выглядеть следующим образом:

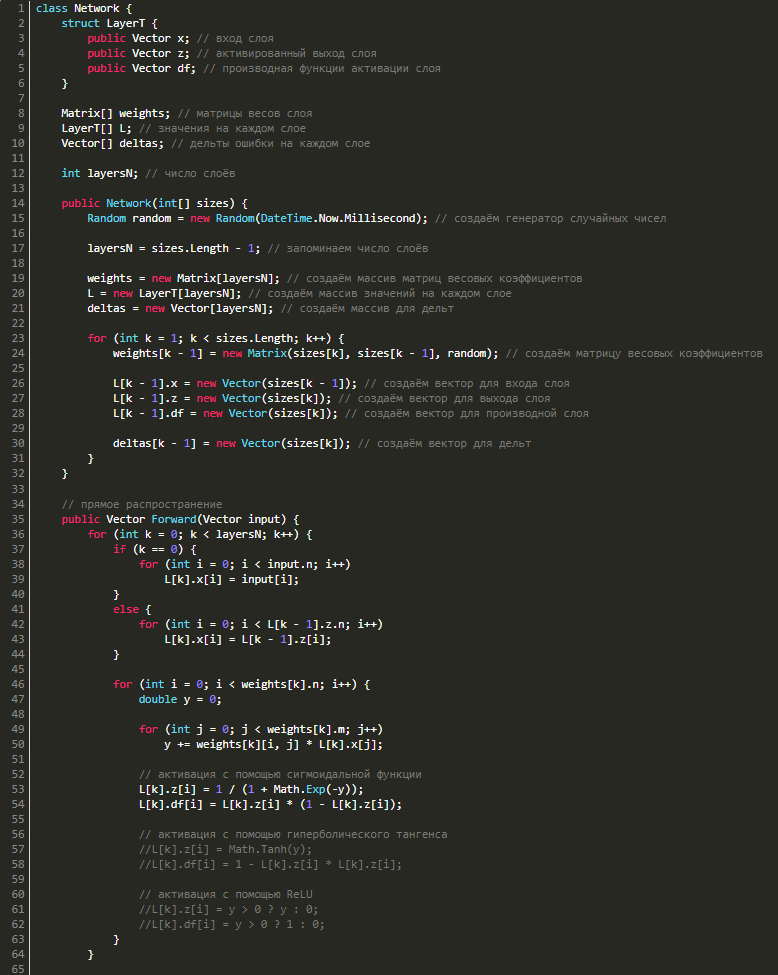
Несколько слов об обратном распространении ошибки

В качестве функции оценки нейросети E(W) мы берем среднее квадратичное отклонение:

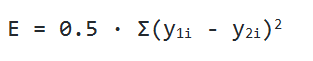
Дабы найти значение ошибки E, надо найти сумму квадратов разности векторных значений, которые были выданы нейронной сетью в виде ответа, а также вектора, который ожидается увидеть при обучении. Еще надо будет найти дельту каждого слоя и учесть, что для последнего слоя дельта будет равняться векторной разности фактического и ожидаемого результатов, покомпонентно умноженной на векторное значение производных последнего слоя:

Когда мы узнаем дельту последнего слоя, мы сможем найти дельты и всех предыдущих слоев. Чтобы это сделать, нужно будет лишь перемножить для текущего слоя транспонированную матрицу с дельтой, а потом перемножить результат с вектором производных функции активации предыдущего слоя:

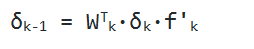
Смотрим реализацию в коде:

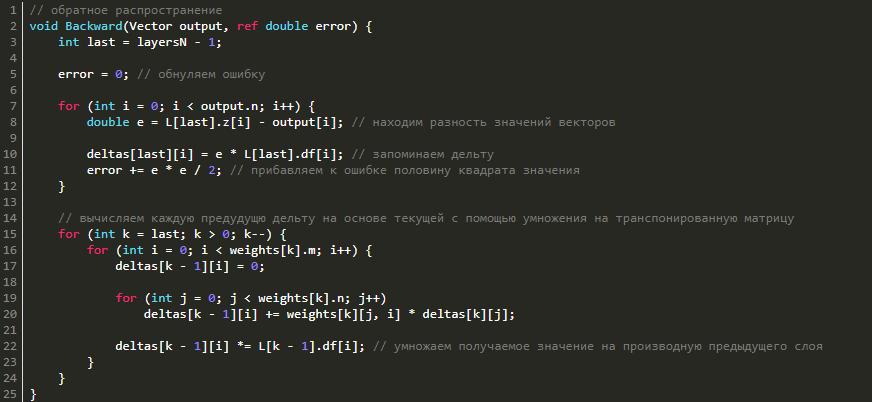
Обновление весовых коэффициентов

Для уменьшения ошибки нейронной сети надо поменять весовые коэффициенты, причем послойно. Каким же образом это осуществить? Ничего сложного в этом нет: надо воспользоваться методом градиентного спуска. То есть нам надо рассчитать градиент по весам и сделать шаг от полученного градиента в отрицательную сторону.

Давайте вспомним, что на этапе прямого распространения мы запоминали входные сигналы, а во время обратного распространения ошибки вычисляли дельты, причем послойно. Как раз ими и надо воспользоваться в целях нахождения градиента. Градиент по весам будет равняться не по компонентному перемножению дельт и входного вектора. Дабы обновить весовые коэффициенты, снизив таким образом ошибку нейросети, нужно просто вычесть из матрицы весов итог перемножения входных векторов и дельт, помноженный на скорость обучения. Все вышеперечисленное можно записать в следующем виде:

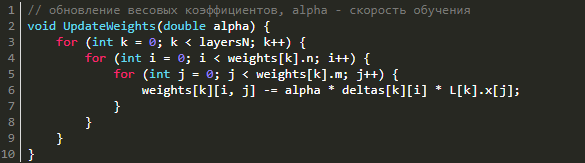
Вот оно, обучение!

Теперь мы имеем все нужные нам методы, поэтому остается лишь всё это вместе соединить, сформировав единый метод обучения.

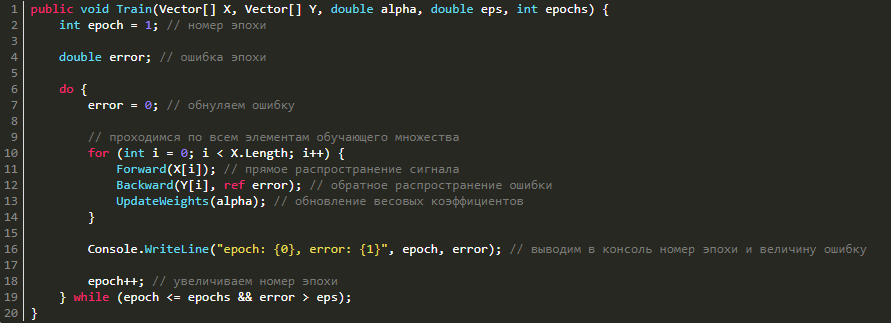
Наша сеть готова, но мы пока ее еще ничему не научили. Сейчас это исправим.

Тренировка нейронной сети. Функции XOR

Функция XOR интересна тем, что ее нельзя получить одним нейроном:

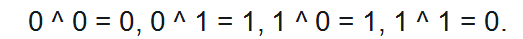
Но ее легко получить путем увеличения количества нейронов. Давайте попробуем реализовать обучение с тремя нейронами в скрытом слое и одним выходным (выход ведь у нас только один). Чтобы все получилось, создадим массив X и Y, имеющий обучающие данные и саму нейронную сеть:

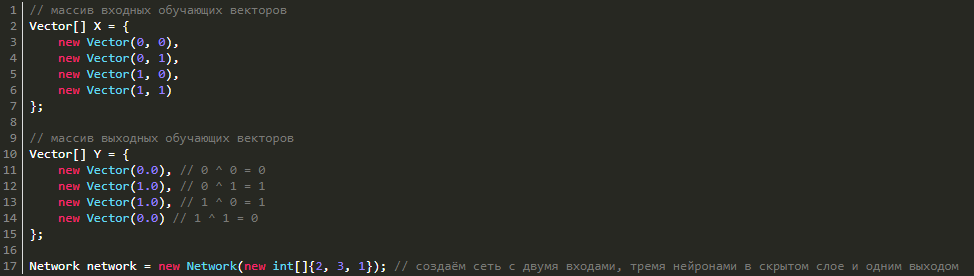
Теперь запускаем обучение с параметрами ниже:

• скорость обучения — 0.5,
• количество эпох — 100000,
• значение ошибки — 1e-7.

Выполнив обучение, посмотрим итоги, для чего надо будет сделать прямой проход для всех элементов:

В итоге вывод будет следующим:

Результаты