
В этой статье мы разберём как сделать калькулятор на Python с использованием библиотеки Tkinter, для создания графического интерфейса или оконного приложения.
Также можете посмотреть прошлую часть где мы познакомились с этой библиотекой, статья называется «Создание графического интерфейса в Python», думаю будет интересно.
Калькулятор на на Python с Tkinter:
Перед тем как начать работать, нужно установить все нужные компоненты, но нам нужно скачать только Tkinter, для этого как всегда для Python прописываем команду PIP.
pip install tk
После того как скачали можете приступать к работе, для этого переходим в ваш файл, где вы будите хранить весь код.
Первым делом нужно импортировать нужные компоненты и создать переменные которые нам пригодятся:
Сделал Python программу для отслеживания курса валют
from tkinter import *
from decimal import *
root . title ( ‘Calculator’ )
buttons = ( ( ‘7’ , ‘8’ , ‘9’ , ‘/’ , ‘4’ ) ,
( ‘4’ , ‘5’ , ‘6’ , ‘*’ , ‘4’ ) ,
( ‘1’ , ‘2’ , ‘3’ , ‘-‘ , ‘4’ ) ,
( ‘0’ , ‘.’ , ‘=’ , ‘+’ , ‘4’ )
Первым делом мы тут как всегда всё импортируем, потом создаём приложение и задаём ему заголовок, потом создаём кортеж кнопок, где каждый картеж, это отдельная строчка кнопок в приложение.
последние мы создаём переменную activeStr, которая отвечает за наспанные числа в строчки ввода, и вторая переменная это список, чисел и команда которые нужно будет выполнить.
Дальше создадим функцию которая будет считать получившийся результат, вот как она будет выглядеть:
def calculate ( ) :
global stack
global label
operand2 = Decimal ( stack . pop ( ) )
operation = stack . pop ( )
operand1 = Decimal ( stack . pop ( ) )
if operation == ‘+’ :
result = operand1 + operand2
if operation == ‘-‘ :
result = operand1 — operand2
if operation == ‘/’ :
result = operand1 / operand2
if operation == ‘*’ :
result = operand1 * operand2
label . configure ( text = str ( result ) )
Как видите в начале функции мы всё раскладываем на числа которые мы получаем и знаки на которые мы нажали, потом всё зависимо от от знака мы считаем вмести эти два числа и в вставляем это в нашу строку ввода.
Теперь перейдём к функции которая будет обрабатывать клик на кнопки там всё гораздо интереснее на мой взгляд.
Вот код функции:
ef click ( text ) :
global activeStr
global stack
if text == ‘CE’ :
stack . clear ( )
label . configure ( text = ‘0’ )
elif ‘0’ <= text <= ‘9’ :
activeStr += text
label . configure ( text = activeStr )
if activeStr . find ( ‘.’ ) == — 1 :
activeStr += text
label . configure ( text = activeStr )
if len ( stack ) >= 2 :
stack . append ( label [ ‘text’ ] )
stack . clear ( )
stack . append ( label [ ‘text’ ] )
stack . append ( text )
stack . append ( label [ ‘text’ ] )
stack . append ( text )
label . configure ( text = ‘0’ )
Как написать свою программу на python? #python #программирование
В начале мы тут проверяем, а нажата ли кнопка CE, если да, то тогда всё удаляем и выводим ноль, иначе если были нажаты цифры, то добавляет это всё в поле ввода, если точка нажата, то тоже добавляем в поле.
Иначе проверяем если у нас stack больше или равен двум, то считаем что у нас получилось и выводим число в поле, которое получилось и если не было нажата равно, то вставляем это число в stack.
Иначе опять проверяем не было ли нажата равно, если нет, то всё так же добавляем значения в список stack.
Последние что нам осталось, так это отрендарить всё приложение, это будет не очень cложно.
Вот код рендара:
label = Label ( root , text = ‘0’ , width = 35 )
label . grid ( row = 0 , column = 0 , columnspan = 4 , sticky = «nsew» )
button = Button ( root , text = ‘CE’ , command = lambda text = ‘CE’ : click ( text ) )
button . grid ( row = 1 , column = 3 , sticky = «nsew» )
for row in range ( 4 ) :
for col in range ( 4 ) :
button = Button ( root , text = buttons [ row ] [ col ] ,
command = lambda row = row , col = col : click ( buttons [ row ] [ col ] ) )
button . grid ( row = row + 2 , column = col , sticky = «nsew» )
root . grid_rowconfigure ( 6 , weight = 1 )
root . grid_columnconfigure ( 4 , weight = 1 )
root . mainloop ( )
По сути мы тут будем создавать таблицу но вначале делаем поле, и потом уже саму таблицу, после того как мы это сделали, первое создаём кнопку «CE», дальше рендрим остальные кнопки, по четыре столбца, это важно, и последние задаём конфигурации для строчки и столбцов, видь как вы поняли по сути мы работаем с таблицей.
Последние запускаем событие цикл который будет отслеживать события нажатия на кнопки, или если по простому то рендерим приложение.
Вывод:
В этой не большой статье вы прочитали как сделать калькулятор на Python с использованием библиотеки Tkinter, думаю вам было интересно, но рекомендую вам самим написать этот код, и поэкспериментировать над ним, чтобы всё ещё лучше понять, как он работает.
Источник: prognote.ru
Основы Java Script



Получить навыки первоначальной настройки среды разработки, получить базовое представление об операторах вывода.
Задания для выполнения
- Установите на компьютер редактор кода Sublime Text 3.
- Установите Google Chrome.
- Создайте новый пустой текстовый файл 1.txt в выбранной директории. Поменяйте разрешение на 1.html и откройте его в Sublime Text 3 и Google Chrome.
- Выведите на экран в браузере Google Chrome сообщение «Hello, World».
- Установить SmartGit
- Сделать клон репозитория https://github.com/al-shatalova/students.git
- Отправить файл на Git со своей фамилией в комментарии (Commit — Push)
Методические указания
Скачать Sublime Text 3 можно с сайта SublimeText (https://www.sublimetext.com/3). После скачивания запустите setup-файл и установите Sublime Text 3.
Скачать Google Chrome можно с сайта (https://www.google.com/intl/en/chrome/). После скачивания запустите setup-файл
Скачать Smart Git можно с сайта: https://www.syntevo.com/smartgit/. После скачивания запустите setup-файл.
Вывести сообщение можно набрав, теги:
Контрольные вопросы
- С какими операционными системами работает Google Chrome?
- Для какой цели служит JavaScript?
- В каких операционных системах работает JavaScript?
- Что означает строчка: ?
Дополнительные задания
Попросите пользователя ввести число и сохраните его в переменную a.
Лабораторная работа №1. Переменные, типы данных
Цель работы
Получить навыки работы с переменными, различными типами данных, операциями над ними.
Задания для выполнения
- Попросите пользователя ввести любое число и сохраните его в переменную.
- Создайте калькулятор, который будет выполнять все арифметические операции над любыми введенными пользователем двумя числами.
- Сохраните калькулятор и отправьте на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_1.
Методические указания
Для запоминания числа можно использовать команду prompt:

Чтобы запустить файл, необходимо запустить его в Google Chrome.
Проверить наличие ошибок можно с помощью нажатия трех точек в верхнем правом углу, затем – Дополнительные инструменты – Инструменты разработчика. В подсказке выдается номер строки, где содержится ошибка.
Вывести на экран значение переменной можно таким образом:

Для перевода в целочисленный тип из строки можно воспользоваться функцией parseInt.
Контрольные вопросы
1. В чем разница между var и let?
- Какие типы данных в Java Script вы знаете?
- В каком типе сохраняется переменная, полученная с помощью команды prompt?
Дополнительные задания
Выведите на экран тип используемой переменной.
Лабораторная работа №2. Оператор ветвления if, циклы do, while, for
Цель работы
Получить навыки работы с циклами и научиться создавать проверку условий средствами Java Script.
Задания для выполнения

- Реализовать представленную блок-схему посредством Java Script
- Напишите программу на Java Script, которая считает от 1 до 10.
- Создайте программу для застолий, которая будет предлагать «Еще по одной?» пока пользователь не введет единицу.
- Загрузите три полученные программы на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_2.
Методические указания
Чтобы создать проверку условия, можно воспользоваться оператором if. Синтаксис:

Для подсчета чисел от 1 до 10 можно воспользоваться циклом While:
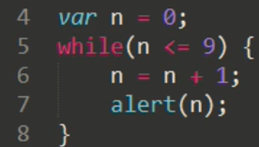

Для реализации программы «Застолье» можно воспользоваться циклом do:

Контрольные вопросы
- Какие условия могут проверяться оператором if?
- В чем отличие циклов while, do, for?
Дополнительные задания
Написать программу «Угадай число»: компьютер загадывает произвольное число и если пользователь угадывает его, компьютер сообщает об этом и выходит из цикла.
Лабораторная работа №3. Массивы и функции
Цель работы
Получить навыки работы с массивами и функциями.
Задания для выполнения
- Организовать симулятор, который выдает только три случайных значения – красный, черный и белый (0, 1, 2). Запустить симуляцию 1000 000 раз. Узнать, какое максимальное число раз выпадало красное значение.
- Реализовать функцию getSum для подсчета суммы очков в массиве карт.
- Загрузить созданные программы на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_3.
Методические указания
Для задания массива достаточно задать: var arr = [];
Для формирования случайного значения можно использовать функцию:
Для обращения к элементам массива можно использовать цикл:
Для подсчета суммы очков в массиве карт можно воспользоваться функцией:

Контрольные вопросы
- Какие значения могут принимать элементы массива?
- Может ли функция описываться позже, чем осуществляться ее вызов?
Дополнительные задания
- Организовать симулятор, который выдает только три случайных значения – красный, черный и белый (0, 1, 2). Запустить симуляцию 1000 000 раз. Узнать, какая последовательность из красных, черных или белых значений была самой длинной.
Лабораторная работа №4. Игра Black Jack
Цель работы
Применить полученные навыки при создании алгоритма для игры в Black Jack.
Задания для выполнения
- Составить алгоритм игры в Black Jack и реализовать его на Java Script.
- Загрузить созданную программы на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_4.
Блэкдже́к (англ. Blackjack «чёрный валет») — одна из самых популярных карточных игр в казино по всему миру. Большая популярность игры обуславливается простыми правилами, скоростью игры и наиболее простой стратегией в подсчёте карт.
Методические указания
Термины
Игрок — Играющий за столом против казино.
Дилер (Крупье) — Работник казино, выполняющий роль чесальщика колоды.
Рука — Набор карт игрока или дилера. Обычно правилами казино игрокам запрещается прикасаться к своим картам.
Трекинг (Tracking) — Отслеживание игроком расположения карт в процессе игры, с использованием этой информации на следующем шаффле.
Шаффл (Shuffle) — Полный «игровой цикл», начинающийся с замешивания колоды, и заканчивающийся выходом разрезной карты.
Башмак, шуз (англ. shoe — ботинок) — Специальное приспособление для карточных игр в казино. Колода перемешивается и вставляется в шуз, из которого потом идет раздача карт.
Фишка (англ. chip) — Плоский небольшой предмет круглой, квадратной или восьмиугольной формы, на котором написан его номинал, может обмениваться на наличные деньги в кассе казино.
Правила
Ошибочно считается, что цель заключается в том, чтобы набрать как можно больше очков, но не более 21. На самом деле цель — обыграть дилера (крупье). В игре используется от одной до восьми колод. Из-за того что вероятность комбинации блек-джек при большем числе колод ниже, то преимущество игрока уменьшается при увеличении числа колод.
При игре с шаффл-машинкой считается, что используется бесконечная колода. По окончании партии, когда осталась примерно треть карт (точное значение устанавливает дилер, размещая специальную карточку в т. наз. «шуз» на глаз), колоды перемешиваются. При игре одной колодой чаще всего она перемешивается после каждой партии.
Значения очков каждой карты: от двойки до десятки — от 2 до 10 соответственно, у туза — 1 или 11 (11 пока общая сумма не больше 21, далее 1), у т. н. картинок (король, дама, валет) — 10.
Если у игрока и дилера число очков на руках равное, то такая ситуация называется «ровно»: за рубежом это называется — пуш (англ. push). В такой ситуации все остаются при своих ставках, никто не выигрывает и не проигрывает. Хотя в казино бывают исключения, и при «пуше» выигрывает казино.
Игроки до раздачи карт делают ставки, кладя фишки на соответствующие поля игрового стола. После того, как первая карта сдана, игрокам запрещается делать ставки и прикасаться к своим фишкам.
Дилер раздаёт карты (обычно из одной или двух колод карт, но чаще из шуза, содержащего не менее четырёх колод): по две карты каждому игроку, себе раздаёт одну карту (в США принято раздавать дилеру две карты, одна из которых открыта, а другая — закрыта, то есть находится на столе рубашкой вверх). Все карты открываются сразу (видны и дилеру, и игроку).
Если у игрока сразу после раздачи набралось 21 очко (то есть у игрока туз и десятиочковая карта), то такая ситуация и называется блек-джек. В таком случае игроку сразу выплачивается выигрыш 3 к 2 (то есть в 1,5 раза превышающий его ставку). Исключение составляют случаи, когда дилеру первой картой (открытой) попадается 10, картинка или туз. В этом случае существует вероятность, что у дилера также будет блек-джек, поэтому игроку с блек-джеком предлагается либо взять выигрыш 1 к 1 (только если первая карта дилера — туз), либо дождаться окончания конца игры (и в случае, если у дилера не блек-джек, получить выигрыш 3 к 2).
Далее игрокам, у которых не блек-джек, предлагается на выбор либо взять ещё карту (в таком случае игрок должен сказать дилеру «карту» или «ещё», англ. hit me), либо остаться при тех картах (и той сумме очков), которые у него на руке (в этом случае игрок должен сказать дилеру «достаточно» или «хватит»).
Как правило, если у игрока после взятия новой карты в сумме получается 21, дилер не спрашивает его больше и переходит к следующему игроку.
Если у игрока после взятия новой карты сумма очков превысит 21, то такая ситуация называется «перебор». Дилер произносит «много» и снимает ставку игрока в пользу казино.
Если у дилера в первых двух картах набирается 21 очко (блек-джек), то все игроки (кроме тех, у кого тоже блек-джек), проигрывают. Те, у которых блек-джек, остаются при своих ставках, если они ранее не выбрали взять выигрыш 1 к 1 или если не застраховали свою комбинацию от блек-джека.
В некоторых случаях, в зависимости от того, какие карты на руках у игрока, дилер может предложить ему дополнительные варианты (см. ниже).
После того, как все игроки завершили брать карты, дилер говорит «себе» и раздаёт карты себе. Общее правило блек-джека состоит в том, что дилер обязан остановиться, как только наберёт 17 очков или выше, и обязан брать, пока не достигнет (даже если у всех не перебравших меньше очков). В различных казино может варьироваться правило, должен ли дилер останавливаться в ситуации, если у него туз и шестёрка (то есть 7 или 17 очков на руке). Обычно это правило написано на игровом столе.
При окончательном подсчёте очков в конце раунда карты остальных игроков для вас значения не имеют, игра ведётся только против дилера, то есть сравниваются карты только игрока и дилера, карты и ставки параллельных игроков не учитываются.
Контрольные вопросы
- Что произойдет при обращении к функциям getRandomInt и getCard?

- Что возвращают функция getSum?

- Что хранится в переменных dealer, player, answer?

- Что делает функция getStatus?

- Что делает цикл do?

- Что выведется на экран?

Лабораторная работа №5. Класс
Цель работы
Получить навыки работы с классами.
Задания для выполнения
- Создайте класс, который будет сохранять в переменную имя пользователя и выводить его на экран. Используйте его.
- Перепишите код с использованием синтаксиса класса:


- Загрузить созданные программы на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_5.
Методические указания
Для задания и вызова класса можно использовать синтаксис:

Базовый синтаксис для классов выглядит так:

Контрольные вопросы
- Для чего нужен класс?
- Как доказать, что класс в JS – это функция?
Дополнительные задания
- Организовать симулятор, который выдает только три случайных значения – красный, черный и белый (0, 1, 2). Запустить симуляцию 1000 000 раз. Узнать, какая последовательность из красных, черных или белых значений была самой длинной.
Лабораторная работа №6. Стрелочные функции
Цель работы
Получить навыки работы с массивами и функциями.
Задания для выполнения
- Создайте пустую стрелочную функцию возвращает undefined
- Создайте массив и напишите стрелочные функции для него: суммирование всех элементов, выявить все четные, умножить каждый элемент на 2.
- Создайте массив с e-mail. Организуйте фильтр на странице html по названию почты.
- Загрузить созданные программы на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_6.
Методические указания
(param1, param2, …, paramN) => statements >
(param1, param2, …, paramN) => expression
// эквивалентно: (param1, param2, …, paramN) =>
// Круглые скобки не обязательны для единственного параметра:
(singleParam) => statements >
singleParam => statements >
// Функция без параметров нуждается в круглых скобках:
() => statements >
() => expression
// Эквивалентно: () =>
// Пустая стрелочная функция возвращает undefined
let empty = () => <>;
(() => ‘foobar’)();
// Удобные операции над массивами: filter, map, .
var arr = [5, 6, 13, 0, 1, 18, 23];
var sum = arr.reduce((a, b) => a + b);
var even = arr.filter(v => v % 2 == 0);
// [6, 0, 18]
var double = arr.map(v => v * 2);
// [10, 12, 26, 0, 2, 36, 46]
Контрольные вопросы
- Из-за чего появилась стрелочная функция?
- Объяснить работу алгоритма:
3. // Стрелочные функции без параметров, которые визуально легче разбирать
4. setTimeout( () =>
5. console.log(‘Я буду раньше’);
6. setTimeout( () =>
7. // deeper code
8. console.log(‘Я буду позже’);
9. >, 1);
10. >, 1);
Лабораторная работа №7. Работа с формами
Цель работы
Получить навыки работы с элементами формы в Java Script.
Задания для выполнения
- Ознакомьтесь с информацией на сайте: https://htmlweb.ru/java/forms.php
- Создайте форму, которая будет запоминать параметры входа (ник и пароль) с валидацией пароля.
- Оформите форму стилями.
- Загрузить созданные программы на GitHub в репозиторий Student, используя формат в названии Фамилия(латинскими буквами)_7.
Методические указания
Форму с валидайцией пароля можно создать следующем образом:
alert(«Ошибка при вводе пароляnПопробуйте еще раз»);
Регистрация
Идентификатор:
onBlur=»this.value=this.value.toUpperCase()»>
Пароль:
onFocus=»this.select();»>
Проверка пароля:
onFocus=»this.select();»>
Cтили можно создать внутри документа:
Глобальные стили
H1
font-family: Verdana, Arial, Helvetica, sans-serif;
Hello, world!
Контрольные вопросы
1. Сколько наборов свойств имеет форма?
2. За что отвечает свойство length?
Источник: mathclub23.ru
Как создать программу для решения уравнений
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Решение квадратного уравнения на С# в Windows Forms.
Сегодня мы напишем программу, которая выведет нам решение квадратного уравнения на С#. Сделаем мы всё это в Windows Forms. В программе мы найдём дискриминант и оба корня.
Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:
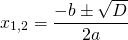
Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:
Теперь пора приступать к программе.
Для начала создаём незамысловатую форму под наши нужды:
Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.
Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.
Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:
Решение квадратного уравнения
Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.
a, b, c — действительные числа, a ≠ 0.
Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.
- если D 0, то уравнение имеет два действительных корня:
- x1 = (-b + √D) / (2⋅a);
- x2 = (-b + √D) / (2⋅a).
Программа для решения квадратного уравнения на языке программирования Паскаль
Функция sqr языка Pascal используется для возведения числа в квадрат.
Функция sqrt используется для получения квадратного корня числа.
В программе используется форматированный вывод вещественных чисел. variable:8:3 — означает, что для вывода переменной предусмотрено 8 символов, 5 из них под целую часть и 3 под дробную.
Программирование решения уравнений

Программирование решения уравнений. Презентация, проект и программный продукт (программа в Pascal)
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Программирование линейных уравнений Работа ученика 9б класса Ф.И.О. обучающегося: Смолькова Андрея Владимировича Руководитель проекта Ф.И.О. Борисова О.А.
Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами . Язык Паскаль – универсальный язык программирования. Никлаус Вирт ( 1934 года рождения) — швейцарский учёный, специалист в области информатики, один из известнейших теоретиков в области разработки языков программирования, профессор информатики (компьютерных наук). Разработчик языка Паскаль и ряда других языков программирования.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Метод Гаусса
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции. Дана непрерывная функция f ( x ), которая содержит единственный корень на отрезке [ a,b ], где b > a при чем определены непрерывны и сохраняют знак f `( x ) f «( x ). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз. Метод Ньютона
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения. Заключение
Предварительный просмотр:
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №7» г. Торжка
Программирование решения уравнений
Работа ученика 9Б класса
Смольков Андрей Владимирович
Ф.И.О. Борисова Ольга Александровна
Работа допущена к защите «_____» _______________ 2018г.
Подпись руководителя проекта _________________(__________________)
Паспорт проекта
Название проекта
Программирование решения уравнений
Руководитель проекта
Борисова Ольга Александровна
Автор проекта
Смольков Андрей Владимирович
Учебная дисциплина
Информатика
Тип проекта
Исследовательский
Цель работы
Изучить программную среду PascalABC для решения уравнений
- Написать программу решения:
- Системы линейных алгебраических уравнений методом Гаусса
- Нелинейных алгебраических уравнений методом Ньютона
Результат проекта (продукт)
Программа в среде программирования PascalABC
Индивидуальный план работы над проектом
Выбор руководителя и темы проекта.
Выбор типа проекта. Составление плана работы над проектом.
Работа над проектом
Анализ теоретической части.
Составление плана защиты проекта.
Отзыв руководителя. Формирование папки индивидуального проекта.
Защита индивидуального итогового проекта
Отзыв
на исследовательскую работу
учащегося 9 б класса МБОУ «Гимназия №7» г. Торжка
Смольков Андрей Владимирович
по теме: «Программирование решения уравнений»
Работа Смолькова Андрея представляет собой исследование программирование решения уравнений. Актуальность работы заключается в том, что на данный момент учащиеся 9-х классов изучают язык программирования Паскаль, и возникла необходимость объединить математику и информатику в единый программный продукт.
В работе важно разобраться с различными методами решения уравнений и написать программу. Содержание работы соответствует заявленной теме. Работа включает в себя основную часть, заключение, список литературы. Работу Андрей выполнял самостоятельно, используя материалы Интернета и литературы.
При выполнения работы Андрей проявил: самостоятельность, способность решать соответствующие проблемы. Не выполнял все рекомендации научного руководителя и не вовремя устранял замечания. Замечания по данной работе значительные, необходимо продумать и доработать заключение по данной теме. Не достаточно теоретического материала по языку программирования и их разновидности.
Вывод: проектная работа Смолькова А.В. по теме: «Программирование решения уравнений» достигла поставленных целей, отвечает требованиям, предъявляемым к индивидуальному итоговому проекту и рекомендуется к защите.
Учитель информатики . Борисова О.А.
(предмет) (подпись) (расшифровка подписи)
«__»_____________ 2018 г.
Общие сведения о языке программирования Паскаль
Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами. Существует несколько тысяч языков программирования. Для данного проекта выбран язык программирования Паскаль, который был разработан в 70-х годах прошлого века Никлаусом Виртом (Швейцария). свое название этот язык получил в честь французского ученого Блеза Паскаля, известного не только своими достижениями в математике, физике и философии, но и созданием первой в мире механической машины, выполнявшей сложение двух чисел.
Язык Паскаль считается универсальным языком программирования, так как он может применяться для записи алгоритмов решения самых разных задач ( вычислительных, обработки текстов, построения графических изображений, поиска информации и т.д.). Он поддерживает процедурный стиль программирования, в соответствии с которым программа представляет собой последовательность операторов, задающих те или иные действия.
Основой языка программирования Паскаль, как и любого другого языка, является алфавит — набор допустимых символов, которые можно использовать для записи программы. Это:
- латинские прописные буквы;
- латинские строчные буквы;
- арабские цифры;
- специальные символы (знак подчеркивания, знаки препинания, круглые, квадратные и фигурные скобки, знаки арифметических операций и д.р.)
В языке существует также некоторое количество различных цепочек символов, рассматриваемых как единые смысловые элементы с фиксированным значением. Такие цепочки символов называются служебными словами.
В программе, записанной на языке Паскаль, можно выделить:
- заголовок программы;
- блок описания используемых данных;
- блок описания действий по преобразованию данных (программный блок).
Общий вид программы:
Решение системы алгебраических уравнений методом Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
В переменную n вводится порядок матрицы системы. С помощью вспомогательной процедуры Input вводятся двумерный массив A и одномерный массив b, после чего оба массива и переменная n передаются функции Gauss. В функции Gauss для каждого k-го шага вычислений выполняется поиск максимального элемента в k-м столбце матрицы начиная с k-й строки.
Номер строки, содержащей максимальный элемент сохраняется в переменной l. В том случае если максимальный элемент находится не в k-й строке, строки с номерами k и l меняются местами. Если же все эти элементы равны нулю, то происходит прекращение выполнения функции Gauss c результатом false. После выбора строки выполняется преобразование матрицы по методу Гаусса.
Решение нелинейных уравнений
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции.
Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f«(x). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз.
К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.
Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.
Заключение
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Язык программирования Паскаль является универсальным языком программирования. В нем можно выполнить самые различные решения уравнений. Язык достаточно прост и понятен для начинающих программистов.
Список литературы
- Босова Л.Л. Информатика: учебник для 8 класса/ Л.Л. босова, А.Ю. Босова.-3-е изд.-М.: БИНОМ. Лаборатория знаний, 2015. — 160с.:ил.
- http://www.cyberforum.ru
- http://tpdn.ru/library/articles/52/13520
- http://pcfu.ru/metod-gaussa-dlya-resheniya-slau
Текст публичного выступления
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса.
Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. На данных слайдах представлен программный продукт реализации решения уравнения методом Гаусса в Паскале.
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции. Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f«(x).
Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз. Программа на слайде.
К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Источник: all-equa.ru