Оператор if мы будем рассматривать прямо в ходе реализации решения квадратного уравнения.
А чтобы реализовать данную задачу, нам надо подумать ход действий. Для начала вспомним, что такое квадратное уравнение:
Квадратное уравнение, это уравнение вида a*x^2 + b*x + c = 0, где a,b,c коэффициенты при иксах.(^2 — возведение в квадрат)
Чтоб найти корни квадратного уравнения, надо найти дискриминант. Обозначим его буквой d:
Так же как мы помним из школьной программы, если дискриминант меньше 0, то решений нет. Если равен 0, то имеется одно решение, если больше 0, то имеем 2 корня.
Корни находятся по формуле:
И так код нашей программы будет выглядеть так:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace ConsoleApplication1
class Program
static void Main(string[] args)
Console.WriteLine(«Введите первый коэффициент»);
int a = Convert.ToInt32(Console.ReadLine());
Как решают уравнения в России и США!?
Console.WriteLine(«Введите второй коэффициент»);
int b = Convert.ToInt32(Console.ReadLine());
Console.WriteLine(«Введите третий коэффициент»);
int c = Convert.ToInt32(Console.ReadLine());
double d;
d = b * b — 4 * a * c;
if (d < 0)
Console.WriteLine(«Дискриминант отрицательный, корней нет»);
>
if (d == 0)
double x1 = -b / (2 * a);
Console.WriteLine(«Дискриминант = 0, x = «, x1);
>
if (d > 0)
double x1 = (-b + Math.Sqrt(Convert.ToDouble(d)))/(2*a);
double x2 = (-b — Math.Sqrt(Convert.ToDouble(d))) / (2 * a);
Console.WriteLine(«Дискриминант = , x1 = , x2 =»,d, x1,x2);
>
>
>
>
Я думаю тут всё ясно, как-раз таки кроме оператора if:
Так же существует оператор else(иначе) и else if, он выполняется, если условие в if не выполняется, то выполняется else. Программно это выглядит так:
if(условие)
код
>
else
код
>
else if(условие)
код
>
Ну вот и всё. Следующие несколько уроков мы будем работать над этой задачей, улучшать её программный код, так как он на данный момент не идеальный.
Источник: karpov-k.me
Подпрограммы
ЗАДАЧА 4.6. Создать программу для решения уравнений:
- линейное
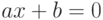 ;
; - квадратное
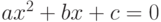 ;
; - кубическое ax^3 + bx^2 + cx + d.

Решение линейного уравнения тривиально: ; алгоритмы решения квадратного и кубического уравнений подробно рассмотрены в задачах 3.4 и 3.5.
Уроки C# / Как сделать первое Windows приложение
Создадим новый проект. Свойства формы настроим по табл. 4.1, за исключением свойства Caption , которому присвоим значение Решение уравнения . Компоненты на форме разместим так, как показано на рис. 4.4.
Обратите внимание, что на форме появились не знакомые нам компоненты. Это CheckBox — флажок и RadioGroup — группа переключателей.
Компонент флажок CheckBox используется для того, чтобы пользователь могут указать свое решение: да или нет. Установлен флажок или нет, определяет свойство Checked (true, false) . В составе диалогового окна может быть несколько таких компонентов, причём состояние любого из них не зависит от состояния остальных.
Компонент группа переключателей RadioGroup объединяет в себе несколько переключателей. Каждый размещённый в нём переключатель помещается в специальный список Items и доступен по номеру, установленному в свойстве ItemIndex . После размещения на форме компонент пуст.
Чтобы создать в нём хотя бы один переключатель , нужно выделить его, обратиться к инспектору объектов и выбрать свойство Items — редактор списка. Строки, набранные в редакторе, используются как поясняющие надписи справа от переключателей, а их количество определяет количество переключателей в группе. В нашем случае окно редактора списка будет иметь вид, как на рис. 4.5.
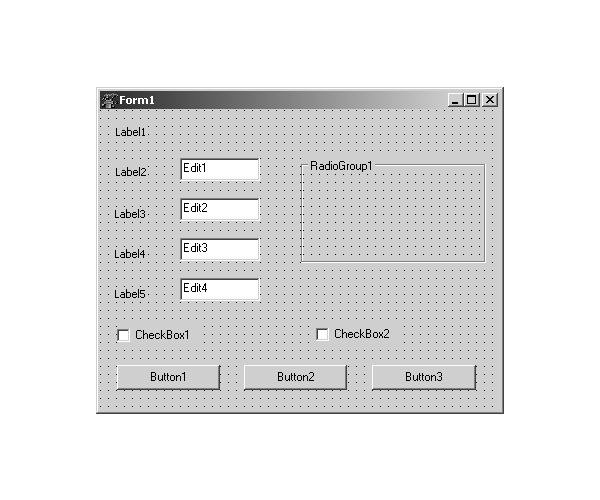
Рис. 4.4. Процесс создания формы к задаче 4.6
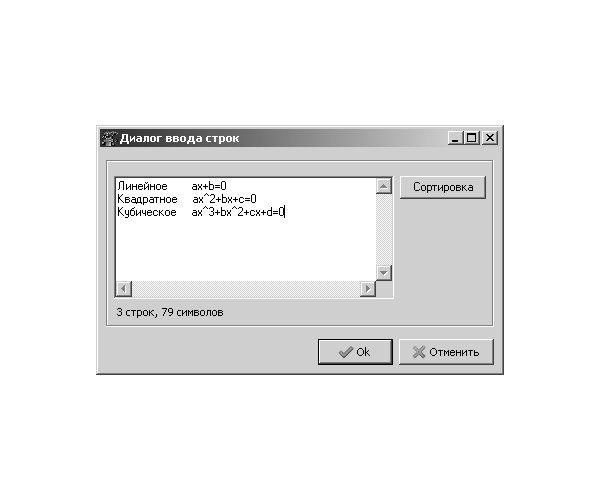
Рис. 4.5. Окно редактора списка
После создания компонента группа переключателей, его свойство номер переключателя ItemIndex по умолчанию равно _1. Это означает, что ни один компонент в группе не установлен. Чтобы в момент появления компонента на экране один из переключателей был отмечен, нужно либо на этапе конструирования формы, либо программно присвоить свойству ItemIndex номер одного из элементов списка, учитывая, что нумерация начинается с нуля.
С остальными компонентами, размещёнными на форме, пользователь уже знаком. На рис. 4.6, рис. 4.7, рис. 4.8 видно, как работает программа . Пользователю предоставляется возможность выбрать вид решаемого уравнения, ввести его коэффициенты и указать, какие решения — действительные или комплексные (если это возможно) — он хотел бы получить.

Рис. 4.6. Решение линейного уравнения
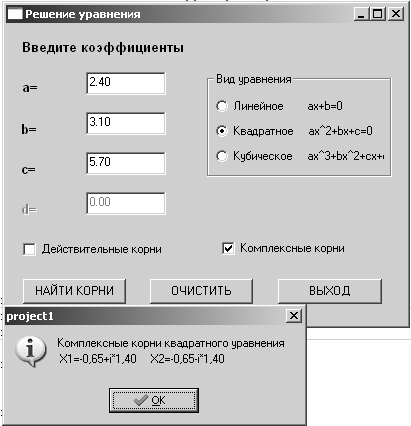
Рис. 4.7. Решение квадратного уравнения
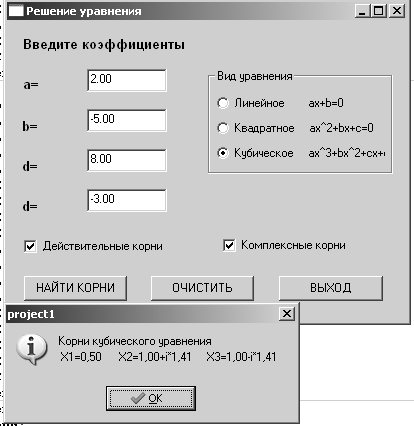
Рис. 4.8. Решение кубического уравнения
Далее приведён текст программного модуля с комментариями:
unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, E x t C t r l s; type TForm1 = class (TForm) Label1 : TLabel; Label2 : TLabel; Label3 : TLabel; Label4 : TLabel; Label5 : TLabel; Edit1 : TEdit; Edit2 : TEdit; Edit3 : TEdit; Edit4 : TEdit; CheckBox1 : TCheckBox; CheckBox2 : TCheckBox; Button1 : TButton; Button2 : TButton; RadioGroup1 : TRadioGroup; Button3 : TButton; procedure FormCreate ( Sender : TObject ); procedure Button2Click ( Sender : TObject ); procedure Button3Click ( Sender : TObject ); procedure Button1Click ( Sender : TObject ); procedure RadioGroup1Click ( Sender : TObject ); private < Private declarations >public < Public declarations >end; var Form1 : TForm1; implementation //Щелчок по кнопке НАЙТИ КОРНИ. procedure TForm1. Button1Click ( Sender : TObject ); //Решение линейного уравнения. procedure korni_1 ( a, b : real; var x_ : string ); var x : real; begin x:=-b/a; x_:= FloatToStrF ( x, ffFixed, 5, 2 ); end; //Решение квадратного уравнения. procedure korni_2 ( a, b, c : real; var x1_, x2_ : string; var pr : byte ); var d, x1, x2 : real; begin d:=b * b-4*a*c; if d0 then u:=exp (1/3 * ln (-q/2+ sqrt ( d ) ) ) else if -q/2+ sqrt ( d)0 then v:=exp (1/3 * ln (-q/2- sqrt ( d ) ) ) else if -q/2- sqrt ( d)0 then //Первый коэффициент не ноль. begin //Решение линейного уравнения. korni_1 (a_, b_, _x ); //Вывод найденного значения.
MessageDlg ( ’Решение линейного уравнения x= ’ +_x, mtInformation, [ mbOk ], 0 ); end else //Первый коэффициент равен нулю, //вывод соответствующего сообщения. MessageDlg ( ’Нет корней ! ’, mtInformation, [mbOk ], 0 ); end else //Некорректный ввод данных. MessageDlg ( ’Ошибка при вводе коэффициентов ! ’, mtInformation, [ mbOk ], 0 ); end; 1 : //Пользователь выбрал второй переключатель из группы. begin //Ввод исходных данных. val ( Edit1. Text, a_, kod_a ); val ( Edit2.
Text, b_, kod_b ); val ( Edit3. Text, c_, kod_c ); //Ввод прошел успешно. if ( kod_a=0) and ( kod_b=0) and ( kod_c=0) then begin if a_<>0 then //Первый коэффициент не ноль. begin //Решение квадратного уравнения. korni_2 (a_, b_, c_, _x1, _x2, _pr ); //В переменной _pr содержится информация //о типе корней: //1 — действительные, 2 — комплексные. //Оба флажка не установлены. if ( CheckBox1. Checked=false ) and ( CheckBox2.
Checked=false ) then MessageDlg ( ’Выберите_тип_решения ’, mtInformation, [ mbOk ], 0 ); //Оба флажка установлены. if CheckBox1. Checked and CheckBox2. Checked then MessageDlg ( ’Решение_квадратного_уравнения ’ +chr (13)+ ’ X1= ’+_x1+ ’ X2= ’+_x2, mtInformation, [ mbOk ], 0 ); //Установлен первый флажок, //корни действительные. if CheckBox1. Checked and ( CheckBox2.
Checked=false ) and ( _pr=1) then MessageDlg ( ’Дейсивительные корни ’, ’квадратного уравнения ’+ chr (13)+ ’ X1= ’+ _x1+ ’ X2= ’+_x2, mtInformation, [ mbOk ], 0 ); //Установлен второй флажок, //корни действительные. if ( CheckBox1. Checked=false ) and CheckBox2. Checked and ( _pr=1) then MessageDlg ( ’Уравнение имеет только ’, ’действительные корни. ’, mtInformation, [ mbOk ], 0 ); //Установлен первый флажок, корни комплексные. if CheckBox1. Checked and ( CheckBox2.
Checked=false ) and ( _pr=2) then MessageDlg ( ’В уравнении действительных ’, ’корней нет ’, mtInformation, [ mbOk ], 0 ); //Установлен второй флажок, корни комплексные. if ( CheckBox1. Checked=false ) and CheckBox2. Checked and ( _pr=2) then MessageDlg ( ’Комплексные корни квадратного ’, ’уравнения ’+ chr (13)+ ’ X1= ’+_x1+ ’ X2= ’+_x2, mtInformation, [ mbOk ], 0 ); end else //Первый коэффициент равен нулю.
MessageDlg ( ’Первый коэффициент не должен быть ’, ’нулевым ! ’, mtInformation, [ mbOk ], 0 ); end //Некорректный ввод данных. else MessageDlg ( ’Ошибка при вводе коэффициентов ! ’, mtInformation, [ mbOk ], 0 ); end; 2 : //Пользователь выбрал третий переключатель из группы. begin //Ввод исходных данных. val ( Edit1. Text, a_, kod_a ); val ( Edit2. Text, b_, kod_b ); val ( Edit3. Text, c_, kod_c ); val ( Edit4.
Text, d_, kod_d ); //Ввод прошел успешно. if ( kod_a=0) and ( kod_b=0) and ( kod_c=0) and ( kod_d=0) then begin if a_<>0 then //Первый коэффициент не ноль. begin //Решение кубического уравнения. //В переменной _pr содержится информация //о типе корней: //1 — действительные, //2 — один действительный и два комплексных. korni_3 (a_, b_, c_, d_, _x1, _x2, _x3, _pr ); //Оба флажка не установлены. if ( CheckBox1. Checked=false ) and ( CheckBox2.
Checked=false ) then MessageDlg ( ’Выберите тип решения ’, mtInformation, [ mbOk ], 0 ); //Оба флажка установлены. if CheckBox1. Checked and CheckBox2. Checked then MessageDlg ( ’Корни кубического ’, ’уравнения ’+ chr (13)+ ’ _X1= ’+_x1+ ’ X2= ’+_x2+ ’ X3= ’+_x3, mtInformation, [ mbOk ], 0 ); //Установлен первый флажок, //корни действительные. if CheckBox1. Checked and ( CheckBox2.
Checked=false ) and ( _pr=1) then MessageDlg ( ’Действительные корни ’, ’кубического уравнения ’+chr (13)+ ’ X1= ’+_x1+ ’ X2= ’+_x2+ ’ X3= ’+_x3, mtInformation, [ mbOk ], 0 ); //Установлен первый флажок, корни комплексные. if CheckBox1. Checked and ( CheckBox2. Checked=false ) and ( _pr=2) then MessageDlg ( ’Действительные корни ’, ’кубического_уравнения ’+chr (13)+ ’ X1= ’+_x1, mtInformation, [ mbOk ], 0 ); //Установлен второй флажок, корни комплексные. if ( CheckBox1. Checked=false ) and CheckBox2.
Checked and ( _pr=2) then MessageDlg ( ’Комплексные корни кубического_ ’, ’уравнения ’+ chr (13)+ ’ X1= ’+_x2+ ’ X2= ’+_x3, mtInformation, [ mbOk ], 0 ); //Установлен второй флажок, //корни действительные. if ( CheckBox1. Checked=false ) and CheckBox2.
Checked and ( _pr=1) then MessageDlg ( ’Уравнение имеет только ’, ’действительные корни. ’, mtInformation, [ mbOk ], 0 ); end else MessageDlg ( ’Первый коэффициент не должен быть ’, ’нулевым ! ’, mtInformation, [ mbOk ], 0 ); end else //Некорректный ввод данных. MessageDlg ( ’Ошибка при вводе коэффициентов ! ’, mtInformation, [ mbOk ], 0 ); end; end; end; //Щелчок по кнопке ОЧИСТИТЬ. procedure TForm1. Button2Click ( Sender : TObject ); begin Label1. Caption := ’Введите коэффициенты ’; Label2.
Caption := ’ a= ’; Label3. Caption := ’ b= ’; Label4. Caption := ’ c= ’; Label5. Caption := ’ d= ’; Edit1. Text := ’ 0.00 ’; Edit2. Text := ’ 0.00 ’; Edit3. Text := ’ 0.00 ’; Edit4. Text := ’ 0.00 ’; Button1.
Caption := ’НАЙТИ КОРНИ ’; Button2. Caption := ’ОЧИСТИТЬ ’; Button3. Caption := ’ВЫХОД ’; CheckBox1. Caption := ’Действительные корни ’; CheckBox2. Caption := ’Комплексные корни ’; CheckBox1.
Checked := true; Label4. Enabled := false; Label5. Enabled := false; Edit3. Enabled := false; Edit4. Enabled := false; CheckBox2. Enabled := false; RadioGroup1. ItemIndex : = 0; end; //Щелчок по кнопке ВЫХОД. procedure TForm1.
Button3Click ( Sender : TObject ); begin close; end; //Событие открытие формы. procedure TForm1. FormCreate ( Sender : TObject ); begin Label1. Caption := ’Введите коэффициенты ’; Label2. Caption := ’ a= ’; Label3. Caption := ’ b= ’; Label4.
Caption := ’ c= ’; Label5. Caption := ’ d= ’; Edit1. Text := ’ 0.00 ’; Edit2. Text := ’ 0.00 ’; Edit3. Text := ’ 0.00 ’; Edit4.
Text := ’ 0.00 ’; Button1. Caption := ’НАЙТИ КОРНИ ’; Button2. Caption := ’ОЧИСТИТЬ ’; Button3. Caption := ’ВЫХОД ’; CheckBox1. Caption := ’Действительные корни ’; CheckBox2. Caption := ’Комплексные корни ’; CheckBox1. Checked := true; Label4.
Enabled := false; Label5. Enabled := false; Edit3. Enabled := false; Edit4. Enabled := false; CheckBox2. Enabled := false; RadioGroup1. ItemIndex : = 0; end; //Выбор переключателя из группы. procedure TForm1. RadioGroup1Click ( Sender : TObject ); begin case RadioGroup1. ItemIndex of 0 : //Выбран первый из списка. begin Label2. Enabled := true; Label3. Enabled := true; Edit1.
Enabled := true; Edit2. Enabled := true; Label2. Caption := ’ a= ’; Label3. Caption := ’ b= ’; Edit1. Text := ’ 0.00 ’; Edit2. Text := ’ 0.00 ’; Label4. Enabled := false; Label5. Enabled := false; Edit3. Enabled := false; Edit4. Enabled := false; CheckBox2.
Enabled := false; end; 1 : //Выбран второй из списка. begin Label2. Enabled := true; Label3. Enabled := true; Label4. Enabled := true; Edit1. Enabled := true; Edit2.
Enabled := true; Edit3. Enabled := true; Label2. Caption := ’ a= ’; Label3. Caption := ’ b= ’; Label4. Caption := ’ c= ’; Edit1.
Text := ’ 0.00 ’; Edit2. Text := ’ 0.00 ’; Edit3. Text := ’ 0.00 ’; Label5. Enabled := false; Edit4. Enabled := false; CheckBox2.
Enabled := true; end; 2 : //Выбран третий из списка. begin Label2. Enabled := true; Label3. Enabled := true; Label4. Enabled := true; Label5. Enabled := true; Edit1. Enabled := true; Edit2. Enabled := true; Edit3.
Enabled := true; Edit4. Enabled := true; Label2. Caption := ’ a= ’; Label3. Caption := ’ b= ’; Label4. Caption := ’ c= ’; Label4.
Caption := ’ d= ’; Edit1. Text := ’ 0. 0 0 ’; Edit2. Text := ’ 0. 0 0 ’; Edit3. Text := ’ 0. 0 0 ’; Edit4. Text := ’ 0. 0 0 ’; CheckBox2.
Enabled := true; end; end; end; end.
Источник: intuit.ru
VIII Международная студенческая научная конференция Студенческий научный форум — 2016


ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ТРЕХДИАГОНАЛЬНОЙ МАТРИЦЕЙ КОЭФФИЦИЕНТОВ
Кичигина А.К. 1 , Свиридова И.В. 1 , Лебединская А.А. 1 , Криволапов Л.А. 1
1 НИУ «БелГУ»
Работа в формате PDF
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Решение систем линейных алгебраических уравнений – одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.
Одна из трудностей практического решения систем большой размерности связанна с ограниченностью оперативной памяти ЭВМ. Хотя объем оперативной памяти вновь создаваемых вычислительных машин растет очень быстро, тем не менее, еще быстрее возрастают потребности практики в решении задач все большей размерности. В значительной степени ограничения на размерность решаемых систем можно снять, если использовать для хранения матрицы внешние запоминающие устройства. Однако в этом случае многократно возрастают как затраты машинного времени, так и сложность соответствующих алгоритмов. Поэтому при создании вычислительных алгоритмов линейной алгебры большое внимание уделяют способам компактного размещения элементов матриц в памятиЭВМ.
К счастью, приложения очень часто приводят к матрицам, в которых число ненулевых элементов много меньше общего числа элементов матрицы. Такие матрицы принято называть разреженными. Одним из основных источников разреженных матриц являются математические модели технических устройств, состоящих из большого числа элементов, связи между которыми локальны. Простейшие примеры таких устройств – сложные строительные конструкции и большие электрические цепи.
Известны примеры решенных в последние годы задач, где число неизвестных достигало сотен тысяч. Естественно, это было бы невозможно, если бы соответствующие матрицы не являлись разреженными (матрица системы из 100 тыс. уравнений в формате двойной точности заняла бы около 75 Гбайт).
Целью работы является: написать программу для реализации численного решения системы линейных алгебраических уравнений с трёхдиагональной матрицей коэффициентов.
Для достижения данной цели необходимо выполнить следующие задачи:
— изучить основные понятия и способы нахождения решения,
— выбрать средства для реализации программы,
Для решения задачи будет использоваться язык программирования C++.
Данный язык программирования широко используется для разработки программного обеспечения, являясь одним из самых популярных языков программирования, а также имеющий очень широкую область применения.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Метод прогонки для решения СЛАУ
Трехдиагональной матрицей или матрицей Якоби называют матрицу следующего вида:
где во всех остальных местах, кроме главной диагонали и двух соседних с ней, стоят нули.
Для решения СЛАУ с трёхдиагональной матрицей используется метод прогонки.[1]
Метод прогонки (англ. tridiagonal matrix algorithm) или алгоритм Томаса (англ. Thomas algorithm) используется для решения систем линейных уравнений вида , где A —трёхдиагональная матрица. Представляет собой вариант метода последовательного исключения неизвестных. Метод прогонки был предложен И. М. Гельфандом и О. В. Локуциевским (в 1952 году; опубликовано в 1960 и 1962 годах), а также независимо другими авторами.[3]
Метод применяется в случае, когда матрица A — трехдиагональная. Сформулируем общую постановку задачи.
Дана система линейных алгебраических уравнений с трехдиагональной матрицей A. Развернутая запись этой системы имеет вид
которому соответствует расширенная матрица:
Здесь первое и последнее уравнения, содержащие по два слагаемых, знак минус (–) при коэффициенте βi взят для более удобного представления расчетных формул метода.
Требуется найти решение системы (1) методом исключения Гаусса.
Если к (1) применить алгоритм прямого хода метода Гаусса, то вместо исходной расширенной матрицы получится трапециевидная:
Учитывая, что последний столбец в этой матрице соответствует правой части, и переходя к системе, включающей неизвестные, получаем рекуррентную формулу:
Соотношение (2) есть формула для обратного хода, а формулы для коэффициентов которые называются прогоночными, определяются из (1), (2). Запишем (2) для индекса и подставим в (1). Получим
Приводя эту формулу к виду (2) и сравнивая, получаем рекуррентные соотношения для
Определение прогоночных коэффициентов по формулам (3) соответствует прямому ходу метода прогонки.
Обратный ход метода прогонки начинается с вычисления . Для этого используется последнее уравнение, коэффициенты которого определены в прямом ходе, и последнее уравнение исходной системы:
Остальные значения неизвестных находятся по рекуррентной формуле (2).[5]
Алгоритм решения систем уравнений методом прогонки
Прямой ход.1. Вычислить (в (3) подставить ).
2. Вычислить прогоночные коэффициенты: по формулам (3).
2. Значения определить по формуле (2):
1. Аналогичный подход используется для решения систем линейных алгебраических уравнений с пятидиагональными матрицами.
2. Алгоритм метода прогонки называется корректным, если для всех , и устойчивым, если .
3. Достаточным условием корректности и устойчивости прогонки является условие преобладания диагональных элементов в матрице , в которой и
и в (5) имеет место строгое неравенство хотя бы при одном .
4. Алгоритм метода прогонки является экономичным и требует для своей реализации количество операций, пропорциональное .[5]
2. ВЫБОР ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Среда разработки Embarcadero C++ Builder XE
Embarcadero C++Builder XE — это на сегодняшний день последняя современная технология и среда для программирования на языке C++, пришедшая на смену многострадальному средству визуальной разработки на языке C++ Builder, которая первоначально разрабатывалась компанией Borland Software, а затем её отдельным подразделением CodeGear, которое сейчас принадлежит компании Embarcadero Technologies, занимающаяся разработкой программного обеспечения для создания средств управления различными базами данных.
С помощью C++Builder XE стало быстрее выполнять работу по созданию высококачественных приложений для Windows-приложений, за счет быстрого написания кода, новых инструментов и компонентов.
При этом сохраняются бесплатные лицензии на прежние старые версии: C++Builder 2010, 2009, 2007 и C++Builder 6, что очень важно для многих программистов использующих язык С++.
По этому, сразу можно сказать, что все старые программы, написанные на Borland C++ Builder 6.0, были легко откомпилированы с помощью Embarcadero C++Builder XE. Сама оболочка стала более понятной и удобной и не вызывала раздражение, как это было в версиях после Borland C++ Builder 6.0.(Рисунок 1).[4]
Рисунок 1 — Среда разработки C++ Builder XE
Средаразработки Microsoft Visual Studio 2012
Microsoft Visual Studio — линейка продуктов компании Microsoft, включающих интегрированную среду разработки программного обеспечения и ряд других инструментальных средств. Данные продукты позволяют разрабатывать как консольные приложения, так и приложения с графическим интерфейсом, в том числе с поддержкой технологии Windows Forms, а также веб-сайты, веб-приложения, веб-службы как в родном, так и в управляемом кодах для всех платформ, поддерживаемых Windows, Windows Mobile, Windows CE, .NET Framework, Xbox, Windows Phone .NET Compact Framework и Silverlight.[2]
Рисунок 2 — Среда разработки Microsoft VS 2012
Visual Studio включает в себя редактор исходного кода с поддержкой технологии IntelliSense и возможностью простейшего рефакторинга кода. Встроенный отладчик может работать как отладчик уровня исходного кода, так и как отладчик машинного уровня.
Среда разработки QtCreator
Qt Creator (ранее известная под кодовым названием Greenhouse) — кроссплатформенная свободная IDE для разработки на С, С++ и QML. Разработана Trolltech (Digia) для работы с фреймворком Qt. Включает в себя графический интерфейс отладчика и визуальные средства разработки интерфейса как с использованием QtWidgets, так и QML. Поддерживаемые компиляторы: GCC, Clang, MinGW, MSVC, Linux ICC, GCCE, RVCT,WINSCW.[2]
Рисунок 3 — Среда разработки Qt Creator
Основная задача Qt Creator — упростить разработку приложения с помощью фреймворка Qt на разных платформах. Поэтому среди возможностей, присущих любой среде разработки, есть и специфичные, такие как отладка приложений на QML и отображение в отладчике данных из контейнеров Qt, встроенный дизайнер интерфейсов как на QML, так и на QtWidgets.
Обоснование выбора среды разработки
В качестве компилятора, для реализации нашей задачи, мы будем использовать Embarcadero C++ Builder XE, подробнее о среде разработки смотрите в пункте 2.1. В программе так же будет присутствовать пользовательский интерфейс. Это связанно с тем, что все вычисления будут происходить не только на этапе компиляции программы.
Почему выбор пал именно на данный вид компилятора? Это связано с тем, что программирование в C++ Builder значительно эффективнее, чем в других средах и платформах C/C++, таких как GCC, Visual C++ и MFC. Библиотека визуальных компонентов (VCL) C++Builder инкапсулирует сложные, трудоемкие интерфейсы Windows API в удобные, расширяемые компоненты многократного применения.
Она полностью интегрирована в среду разработки и двусторонние визуальные конструкторы. Это облегчает управление свойствами и методами компонентов через программный код и в визуальном режиме. В результате при разработке приложений с помощью библиотеки VCL приходится писать, отлаживать и тестировать до 5 раз меньше программных строк без ухудшения производительности и функциональных возможностей. Приложения, созданные с использованием компонентов, отличаются более высоким качеством, они удобнее в обслуживании и легче поддаются изменению.[4]
3. ОПИСАНИЕ РЕАЛИЗАЦИИ ПРОГРАММЫ
После анализа предметной области можно переходить к программной реализации.
В качестве языка программирования для реализации алгоритма был выбран язык С++. Это очень мощный язык, позволяющий создавать программы любого назначения и любой сложности. Поддерживаются множество стилей программирования, включая ООП. Имеется возможность прямой работы с памятью.
Определившись с выбором подходящего компилятора, можно приступать к написанию самой программы.
Реализация алгоритма решения СЛАУ
Рассмотрим основное тело программы, написанное в файле Unit1.cpp.
Первым делом, мы видим заголовочные файлы форм Unit1.h и Unit2.h Листинг 1.1.
Листинг 1.1. Заголовочные файлы форм
Дальше идёт объявление переменной (AnsiString num), а которой хранится вся информация о размере таблицы.
В следующей части находится событие, которое выполняется при нажатии на кнопку Button. Листинг 1.2.
Листинг 1.2. Событие Button1Click
void __fastcall TForm1::Button1Click(TObject *Sender)
Далее рассмотрим основное тело программы, написанное в файле Unit2.cpp.
Здесь мы видим событие после показа формы. Как только в первой форме выполняется команда Form2->Show(), сразу выполняется код в этом событии. Листинг 1.3.
Листинг 1.3. Событие FormShow
void __fastcall TForm2::FormShow(TObject *Sender)
int n = StrToInt(n1);
Далее выделяется память под массив типа float размером NxN и предоставляются следующие переменные для наглядного вывода. Листинг 1.4.
Листинг 1.4. Выделение памяти под массив
float *base = (float*)calloc(n*(n + 1), sizeof(float));
String st= «Введите «;
Следующая часть служит для ввода данных. В данном цикле создаются окна для ввода Input — это и есть вызов окна с параметрами. После ввода строки матрицы она добавляется в ListBox для наглядного отображения. Листинг 1.5.
Листинг 1.5. Ввод данных
for (int i = 0; iItems->Add(st1);
Далее идёт выделение массивов для вспомогательных коэффициентов, расчёт и вывод первых и всех остальных коэффициентов по формулам. Также происходит выделение памяти под массив ответов. Листинг 1.6.
Листинг 1.6. Выделение массивов, расчёт и вывод коэффициентов
//Выделение массивов для вспомогательных коэффициентов
float *alpha; float *betta;
alpha = (float*)calloc(n, sizeof(float));
betta = (float*)calloc(n, sizeof(float));
//Расчет и вывод первых коэффициентов
*alpha = -*(base + 1) / *base;
*betta = *(base + n) / *base;
//В этом цикле производится расчет всех остальных коэффициентов.
for (int i = 1; i= 0; i—)
*(ans + i) = *(alpha + i)**(ans + i + 1) + *(betta + i);
В следующей части, в элемент ListBox добавляются по очереди корни, которые выводятся на форму, каждый с новой строки. А далее находится событие, которое выполняется при нажатии на кнопку FormClose. И, в заключении, программа закрывается. Листинг 1.8.
Листинг 1.8.Вывод корней на экран
for (int i = 0; iItems->Add(st);
void __fastcall TForm2::FormClose(TObject *Sender, TCloseAction в третьем уравнении , в четвертом уравнении . Далее выполняем прямой и обратный ход, учитывая, что расширенная матрица имеет вид:
1. Прямой ход. Вычислим прогоночные коэффициенты:
Подчеркнем, что , так как в (10.2) во втором слагаемом взят знак «минус»:
Подстановкой решения в исходную систему убеждаемся, что задача решена верно. Для данного примера , т.е. метод прогонки оказался корректным и устойчивым (см. пункт 3 замечаний 10.3).
Для наглядности представления информации исходные данные и результаты расчетов поместим в табл. 10.1, где в первых четырех колонках содержатся исходные данные, а в последних трех — полученные результаты. Таблица 1.1.
Исходные данные и результаты расчётов
Результат работы созданного программного обеспечения
Для начала производим ввод данных, то есть указываем размерность нашей будущей матрицы. (Рисунок 4).
Рисунок 4 — Ввод данных о размерности матрицы.
Далее по очереди вводим элементы 1 строки нашей матрицы и элемент столбца правой части системы, как указано на рисунках 5 и 6 соответственно:
Рисунок 5 — Ввод элементов первой строки
Рисунок 6 — Ввод элемента столбца правой части системы.
То же самое проделываем с остальными строками, в зависимости от размера матрицы. Закончив с вводом данных, мы получаем итоговое окно, где можем наблюдать окна с выводом нашей системы линейных алгебраических уравнений и её корнями. (Рисунок 7).
Рисунок 7 — Вывод СЛАУ и её корней.
При выполнении работы вручную и с помощью программы, мы можем сделать вывод, что вычисление происходит с небольшой погрешностью в 0,0001, что с правильным округлением значения приводит к верному ответу. Следовательно, можно сделать вывод, что программа работает правильно. Результаты можно увидеть в приведенной ниже таблице 2.
ЗАКЛЮЧЕНИЕ
Численные методы являются одним из мощных математических средств решения задачи. Простейшие численные методы мы используем всюду, например, извлекая квадратный корень на листке бумаги. Есть задачи, где без достаточно сложных численных методов не удалось бы получить ответа; классический пример – открытие Нептуна по аномалиям движения Урана.
Одним из самых распространенных методов решения систем линейных уравнений является метод прогонки. Условие преобладания диагональных элементов обеспечивает также устойчивость метода прогонки относительно погрешностей округлений. Последнее обстоятельство позволяет использовать метод прогонки для решения больших систем уравнений. Метод прогонки оказывается устойчивым даже при нарушении условия преобладания диагональных элементов.
В ходе выполнения курсовой работы мы проделали ручной расчет заданного уравнения, выполнили расчет на языке программирования C++.