Как сделать программу на python быстрее

В этой статье автор разобрался, как увеличить скорость работы Python, и продемонстрировал реализацию на реальном примере.

Прим. ред. Это перевод. Мнение редакции может не совпадать с мнением автора оригинала.

Тест базовой скорости

Для сравнения базовой скорости Python и C++ я буду использовать алгоритм генерации случайных простых чисел.

Реализация на Python

Реализация на C++

Результат

• Python: скорость выполнения 80,137 секунд;
• C++: скорость выполнения 3,174 секунды.

Комментарий

Как и ожидалось, программа на C++ выполняется в 25 раз быстрее, чем на Python. Ожидания подтвердились, потому что:

• Python — это динамически типизированный язык;
• GIL(Python Global Interpreter) — не поддерживает параллельное программирование.

Благодаря тому, что Python это гибкий универсальный язык, наш результат можно улучшить. Один из лучших способов увеличить скорость Python — Numba.

Numba

Numba — это Open Source JIT-компилятор, который переводит код на Python и NumPy в быстрый машинный код.

Чтобы начать использовать Numba, просто установите её через консоль:

Как выучить Python БЫСТРО используя ChatGPT?

Реализация на Python с использованием Numba

Как вы могли заметить, в коде добавились декораторы njit:

• parallel=True — включает параллельное выполнение программы на процессоре;
• fastmath=True — разрешает использование небезопасных преобразований с плавающей точкой;
• cache=True — позволяет сократить время компиляции функции, если она уже была скомпилирована.

Итоговая скорость Python

• Python: скорость выполнения 1,401 секунды;
• C++: скорость выполнения 3,174 секунды.

Теперь вы знаете что Python способен обогнать C++. О других способах увеличения скорости работы Python читайте в статье про пять проектов, которые помогают ускорить код на Python.

Источник: news.myseldon.com

Быстрая сортировка в Python

Быстрая сортировка – популярный алгоритм сортировки, который часто используется вместе с сортировкой слиянием. Это алгоритм является хорошим примером эффективного алгоритма сортировки со средней сложностью O(n logn). Часть его популярности еще связана с простотой реализации.

Спонсор поста Онлайн-курс по алгоритмам на Python

Курс по алгоритмам и структурам данных на Python для новичков. Видео-уроки, домашние задания, поддержка. На курсе вы изучите следующие темы:
– Структуры данных, сортировка и поиск.
– Рекурсия, деревья, сжатие информации.
– Криптография и и блокчейн.

С 2019 года курс «читается» студентам Московского университета экономики и права им. Витте на специальностях «Прикладная информатика» и «Бизнес-информатика».

Самый простой способ выучить Python | Топовые фишки Пирамиды Обучения

Быстрая сортировка является представителем трех типов алгоритмов: divide and conquer (разделяй и властвуй), in-place (на месте) и unstable (нестабильный).

• Divide and conquer: Быстрая сортировка разбивает массив на меньшие массивы до тех пор, пока он не закончится пустым массивом, или массивом, содержащим только один элемент, и затем все рекурсивно соединяется в сортированный большой массив.
• In place: Быстрая сортировка не создает никаких копий массива или его подмассивов. Однако этот алгоритм требует много стековой памяти для всех рекурсивных вызовов, которые он делает.
• Unstable: стабильный (stable) алгоритм сортировки – это алгоритм, в котором элементы с одинаковым значением отображаются в том же относительном порядке в отсортированном массиве, что и до сортировки массива. Нестабильный алгоритм сортировки не гарантирует этого, это, конечно, может случиться, но не гарантируется. Это может быть важным, когда вы сортируете объекты вместо примитивных типов. Например, представьте, что у вас есть несколько объектов Person одного и того же возраста, например, Дейва в возрасте 21 года и Майка в возрасте 21 года. Если бы вы использовали Quicksort в коллекции, содержащей Дейва и Майка, отсортированных по возрасту, нет гарантии, что Дейв будет приходить раньше Майка каждый раз, когда вы запускаете алгоритм, и наоборот.

Быстрая сортировка

Базовая версия алгоритма делает следующее:

Разделяет коллекцию на две (примерно) равные части, принимая псевдослучайный элемент и использовать его в качестве опоры (как бы центра деления). Элементы, меньшие, чем опора, перемещаются влево от опоры, а элементы, размер которых больше, чем опора, справа от него. Этот процесс повторяется для коллекции слева от опоры, а также для массива элементов справа от опоры, пока весь массив не будет отсортирован.

Когда мы описываем элементы как «больше» или «меньше», чем другой элемент – это не обязательно означает большие или меньшие целые числа, мы можем отсортировать по любому выбранному нами свойству.

К примеру, если у нас есть пользовательский класс Person, и у каждого человека есть имя и возраст, мы можем сортировать по имени (лексикографически) или по возрасту (по возрастанию или по убыванию).

Как работает Быстрая сортировка

Быстрая сортировка чаще всего не сможет разделить массив на равные части. Это потому, что весь процесс зависит от того, как мы выбираем опорный элемент. Нам нужно выбрать опору так, чтобы она была примерно больше половины элементов и, следовательно, примерно меньше, чем другая половина элементов. Каким бы интуитивным ни казался этот процесс, это очень сложно сделать.

Подумайте об этом на мгновение – как бы вы выбрали адекватную опору для вашего массива? В истории быстрой сортировки было представлено много идей о том, как выбрать центральную точку – случайный выбор элемента, который не работает из-за того, что «дорогой» выбор случайного элемента не гарантирует хорошего выбора центральной точки; выбор элемента из середины; выбор медианы первого, среднего и последнего элемента; и еще более сложные рекурсивные формулы.

Самый простой подход – просто выбрать первый (или последний) элемент. По иронии судьбы, это приводит к быстрой сортировке на уже отсортированных (или почти отсортированных) массивах.

Именно так большинство людей выбирают реализацию быстрой сортировки, и, так как это просто и этот способ выбора опоры является очень эффективной операцией, и это именно то, что мы будем делать.

Теперь, когда мы выбрали опорный элемент – что нам с ним делать? Опять же, есть несколько способов сделать само разбиение. У нас будет «указатель» на нашу опору, указатель на «меньшие» элементы и указатель на «более крупные» элементы.

Цель состоит в том, чтобы переместить элементы так, чтобы все элементы, меньшие, чем опора, находились слева от него, а все более крупные элементы были справа от него. Меньшие и большие элементы не обязательно будут отсортированы, мы просто хотим, чтобы они находились на правильной стороне оси. Затем мы рекурсивно проходим левую и правую сторону оси.

Рассмотрим пошагово то, что мы планируем сделать, это поможет проиллюстрировать весь процесс. Пусть у нас будет следующий список.

29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21,44 (high)

Выберем первый элемент как опору 29), а указатель на меньшие элементы (называемый «low») будет следующим элементом, указатель на более крупные элементы (называемый «high») станем последний элемент в списке.

29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21 (high),44

• Мы двигаемся в сторону high то есть влево, пока не найдем значение, которое ниже нашего опорного элемента.

29 | 99 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,21 (high),44

• Теперь, когда наш элемент high указывает на элемент 21, то есть на значение меньше чем опорное значение, мы хотим найти значение в начале массива, с которым мы можем поменять его местами. Нет смысла менять местами значение, которое меньше, чем опорное значение, поэтому, если low указывает на меньший элемент, мы пытаемся найти тот, который будет больше.
• Мы перемещаем переменную low вправо, пока не найдем элемент больше, чем опорное значение. К счастью, low уже имеет значение 89.
• Мы меняем местами low и high:

29 | 21 (low),27,41,66,28,44,78,87,19,31,76,58,88,83,97,12,99 (high),44

• Сразу после этого мы перемещает high влево и low вправо (поскольку 21 и 89 теперь на своих местах)
• Опять же, мы двигаемся high влево, пока не достигнем значения, меньшего, чем опорное значение, и мы сразу находим – 12
• Теперь мы ищем значение больше, чем опорное значение, двигая low вправо, и находим такое значение 41

Этот процесс продолжается до тех пор, пока указатели low и high наконец не встретятся в одном элементе:

29 | 21,27,12,19,28 (low/high),44,78,87,66,31,76,58,88,83,97,41,99,44

• Мы больше не используем это опорное значение, поэтому остается только поменять опорную точку и high, и мы закончили с этим рекурсивным шагом:

28,21,27,12,19,29,44,78,87,66,31,76,58,88,83,97,41,99,44

Как видите, мы достигли того, что все значения, меньшие 29, теперь слева от 29, а все значения больше 29 справа.

Затем алгоритм делает то же самое для коллекции 28,21,27,12,19 (левая сторона) и 44,78,87,66,31,76,58,88,83,97,41,99,44 (правая сторона). И так далее.

Реализация

Сортировка массивов

Быстрая сортировка является естественным рекурсивным алгоритмом – разделите входной массив на меньшие массивы, переместите элементы в нужную сторону оси и повторите.

При этом мы будем использовать две функции – partition() и quick_sort().

Давайте начнем с функции partition():

def partition(array, begin, end): pivot = begin for i in xrange(begin+1, end+1): if array[i]

И, наконец, давайте реализуем функцию quick_sort():

def quick_sort(array, begin=0, end=None): if end is None: end = len(array) — 1 def _quicksort(array, begin, end): if begin >= end: return pivot = partition(array, begin, end) _quicksort(array, begin, pivot-1) _quicksort(array, pivot+1, end) return _quicksort(array, begin, end)

После того, как обе функции реализованы, мы можем запустить quick_sort():

array = [29,19,47,11,6,19,24,12,17,23,11,71,41,36,71,13,18,32,26] quick_sort(array) print(array)
[6, 11, 11, 12, 13, 17, 18, 19, 19, 23, 24, 26, 29, 32, 36, 41, 47, 71, 71]

Поскольку алгоритм unstable (нестабилен), нет никакой гарантии, что два 19 будут всегда в этом порядке друг за другом. Хотя это ничего не значит для массива целых чисел.

Оптимизация быстрой сортировки

Учитывая, что быстрая сортировка сортирует «половинки» заданного массива независимо друг от друга, это оказывается очень удобным для распараллеливания. У нас может быть отдельный поток, который сортирует каждую «половину» массива, и в идеале мы могли бы вдвое сократить время, необходимое для его сортировки.

Однако быстрая сортировка может иметь очень глубокий рекурсивный стек вызовов, если нам особенно не повезло в выборе опорного элемента, а распараллеливание будет не так эффективно, как в случае сортировки слиянием.

Для сортировки небольших массивов рекомендуется использовать простой нерекурсивный алгоритм. Даже что-то простое, например сортировка вставкой, будет более эффективным для небольших массивов, чем быстрая сортировка. Поэтому в идеале мы могли бы проверить, имеет ли наш подмассив лишь небольшое количество элементов (большинство рекомендаций говорят о 10 или менее значений), и если да, то мы бы отсортировали его с помощью Insertion Sort (сортировка вставкой).

Заключение

Как мы уже упоминали ранее, эффективность быстрой сортировки сильно зависит от выбора точки опоры – он может «упростить или усложнить» сложность алгоритма во времени (и в пространстве стека). Нестабильность алгоритма также может стать препятствием для использования с пользовательскими объектами.

Тем не менее, несмотря на все это, средняя сложность времени O(n*logn) в быстрой сортировки, а также его относительно небольшое потребление памяти и простая реализация делают его очень эффективным и популярным алгоритмом.

Источник: webdevblog.ru

Мемоизация в Python для ускорения медленных функций

В данном руководстве мы рассмотрим использование функций lru_cache и cache для оптимизации расчетов в функциях Python.

Введение

Мемоизация — это техника оптимизации, которая ускоряет работу программ за счет кэширования результатов предыдущих вызовов функций. Это позволяет последующим вызовам повторно использовать кэшированные результаты, избегая трудоемкого пересчета.

Числа Фибоначчи

Числа Фибоначчи — это последовательность целых чисел, где каждое число является суммой двух предыдущих чисел, начиная с чисел 0 и 1.

Функция, которая вычисляет n-ое число Фибоначчи, часто реализуется рекурсивно.

Посмотрим на пример реализации

def fibonacci(n): if n

Вызовы функций fibonacci(4) можно визуализировать с помощью дерева рекурсии.

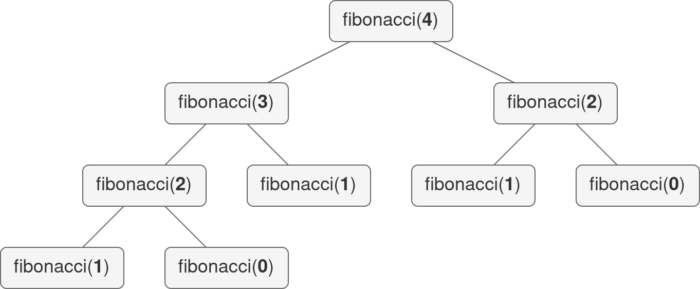
Обратите внимание, что функция вызывается с одним и тем же входом несколько раз. В частности, fibonacci(2) вычисляется с нуля дважды. По мере увеличения входных данных время работы растет экспоненциально. Это неоптимальный вариант, который можно значительно улучшить с помощью мемоизации.

Мемоизация в Python

В Python 3 запоминать функции невероятно просто. Модуль functools, входящий в стандартную библиотеку Python, предоставляет два полезных декоратора для мемоизации: lru_cache (новый в Python 3.2) и cache (новый в Python 3.9). Эти декораторы используют кэш с наименьшим последним использованием (LRU), который хранит элементы в порядке их использования, отбрасывая наименее недавно использованные элементы, чтобы освободить место для новых.

Чтобы избежать дорогостоящих повторных вызовов функций, fibonacci может быть обернут lru_cache, который сохраняет значения, которые уже были вычислены. Предельный размер lru_cache можно задать с помощью параметра maxsize, значение которого по умолчанию равно 128.

Теперь дерево рекурсии для fibonacci(4) не имеет узлов, которые встречаются более двух раз. Время работы теперь растет линейно, что гораздо быстрее экспоненциального роста.

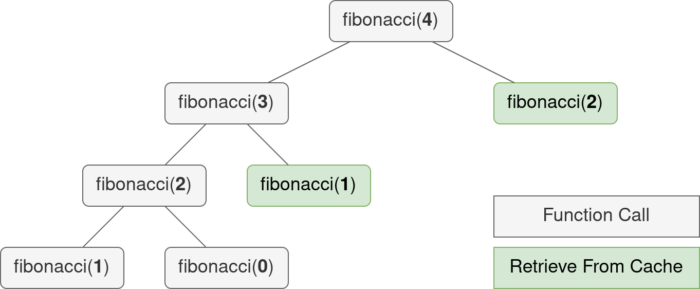
Декоратор cache эквивалентен lru_cache(maxsize=None).

Поскольку cache не нуждается в отбрасывании последних использованных элементов, он одновременно меньше и быстрее, чем lru_cache с ограничением размера.

Заключение

Мемоизация повышает производительность за счет кэширования результатов вызовов функций и возврата кэшированного результата при повторном вызове функции с теми же входными данными.

Python 3 позволяет легко реализовать мемоизацию. Просто импортируйте lru_cache или cache из functools и примените декоратор.

Источник: egorovegor.ru