Руководство компании по результатам производственной деятельности 15 своих филиалов в различных городах России анализирует факторы, влияющие на производительность труда (y) и предполагает, что важнейшими из них являются следующие:
x1 – среднегодовая стоимость основных фондов, тыс. руб.
х2 – удельный вес рабочих высокой квалификации в общей численности рабочих, %
х3 – трудоемкость единицы продукции
х4 – среднегодовая численность рабочих
x5 – коэффициент сменности оборудования
x6 – удельный вес потерь от брака
x7 – среднегодовой фонд заработной платы, тыс. руб.
Были собраны данные за последний год (см. таб. 3).
Таблица 1 – Исходные данные
3.2 Выполнение анализа
1. Для y и независимых переменных (факторные признаки) х1, х2, х4, x5 построить матрицу частных коэффициентов корреляции (корреляционную матрицу). Изобразить матрицу в графическом виде.
Порядок выполнения задания
В системе STATISTICA для построения корреляционной матрицы можно воспользоваться модулем Basic Statistics/Tables (Основные статистики и таблицы), выбрав процедуры 
, используя в качестве переменныхх1, х2, х4, x5.
КОРРЕЛЯЦИЯ Спирмена Пирсона Кенделла | АНАЛИЗ ДАННЫХ #12
И процедуру для представления матрицы в графическом виде.
По корреляционной матрице можно в первом приближении судить о тесноте связи факторных признаков х1, х2,…,xm между собой и с результативным признаком y, а также осуществлять предварительный отбор факторов для включения их в уравнение регрессии. При этом не следует включать в модель факторы, слабо коррелирующие с результативным признаком и тесно связанные между собой. Не допускается включать в модель функционально связанные между собой факторные признаки, так как это приводит к неопределенности решения.
2. Построить линейное уравнение множественной регрессии, выбрав в качестве зависимой переменной – y, в качестве независимых – переменные х1, х2, х4, x5 .
1) Определить коэффициент множественной корреляции и коэффициент детерминации R 2 полученной модели.
2) Проверить значимость построенной модели (например, используя уровень значимости α=0,05).
3) Если модель значима дать оценку коэффициентов множественной регрессии на основе t-критерия, если tтабл(15-4-1)= tтабл(10)=2,2281 и уровня значимости α=0,05.
4) Пересчитать уравнение множественной регрессии, используя только значимые факторы.
5) Проверить адекватность регрессионной модели (полученной на предыдущем этапе анализа).
6) Осуществить прогнозирование: Как изменится производительность труда на московском предприятии, если среднегодовую численность рабочих сократить на 780 человек, а коэффициент сменности оборудования повысить до 3?
КОРРЕЛЯЦИЯ Спирмена Пирсона STATISTICA #08
7) Оформить отчет о проделанной работе в MS Word.
Порядок выполнения задания
Выбор уравнения модели, в большинстве случаев, производятся среди функций перечисленных в таблице 3. В системе STATISTICA для построения линейного уравнения множественной регрессии можно воспользоваться модулем множественной регрессии , определив зависимую (dependent) переменнуюy и независимые (independent) переменные х1, х2, x3, x4.
Статистический вывод о пригодности (значимости) уравнения регрессии в системе Statistica обычно проверяется в следующей последовательности.
1. Проводится общая проверка модели, целью которой является выяснение, объясняют ли х-переменные значимую долю изменения у. Определение значимости модели рекомендуется проводить по следующим методам (см. табл. 5).
Критерий Фишера
Использование уровня
значимости α
Использование коэффициента детерминации R 2
Проверяется нулевая гипотеза H0 о равенстве полученных коэффициентов регрессии нулю: a0=a1=a2=…=am=0. Для этого рассчитанное системой Statistica значение F-критерия (Fрасч), сравнивается с табличным значением Fтабл, определяемым с использованием специальных таблиц по заданным уровню значимости (например, =0,05) и числу степеней свободы (df1=m, df2=n-m-1). Если выполняется неравенство Fрасч < Fтабл, то с уверенностью, например на 95 %, можно утверждать, что рассматриваемая зависимость y = а0 + a1x1+ … +amxm является статистически значимой.
Если рассчитанное в Statistica значение уровня значимости р больше, чем заданный уровень значимости (например, =0,05), то полученный результат нужно трактовать как незначимый
Рассчитанная системой Statistica величина 
сравнивается с табличными (критическими) значениями
, определяемым с использованием специальных таблиц по заданному уровню значимости (например, α =0,05). Если окажется, что 
>
, то с упомянутой степенью вероятности (95 %) можно утверждать, что анализируемая регрессия является значимой.
Если регрессия не является значимой, то говорить больше не о чем.
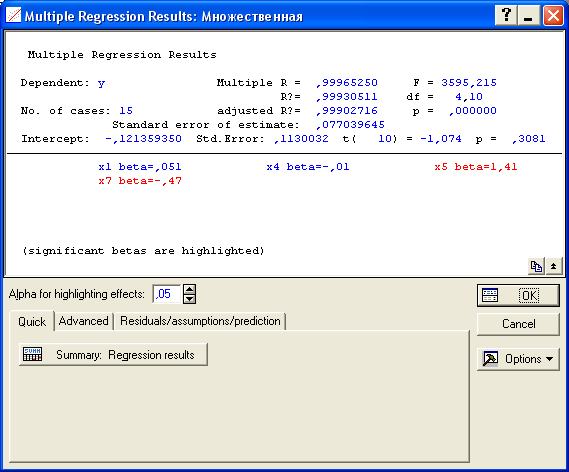
Осуществив переход к результатам регрессии (Summary: Regression results), получаем уравнение линейной множественной регрессии вида
y(x1, x2, x3, x4)=6,9+0,07×1 –0,00035×2–2,08×3+0,00003×4:
2. Если регрессия оказывается значимой, то существует взаимосвязь между параметром у и переменными х1, х2,…,xm. Однако остается неясно, каково влияние конкретных факторов х1, х2,…,xm на исследуемую функцию у. Можно продолжить анализ, используя t-тесты для отдельных коэффициентов регрессии а0, a1, a2,…,am с целью выяснить, насколько значимой является влияние той или иной переменной х на параметр у при условии, что все другие факторы хk остаются неизменными. Проверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам (см. табл. 5).
Использование t-критерия Стьюдента
Использование
уровня значимости α
Анализируемый коэффициент а0, a1, a2,…,am считается значимым, если рассчитанное системой Statistica для него значение t-критерия по абсолютной величине превышает tтабл, определяемым с использованием специальных таблиц по заданным уровню значимости (например, =0,05) и числу степеней свободы (df=n-m-1).
Коэффициент регрессии а0, a1, a2,…,am признается значимым, если рассчитанное системой Statistica для него значение уровня значимости р меньше (или равно) 0,05 (для 95%-ной доверительной вероятности).
Т.к. вычисленные уровни значимости p-level для коэффициентов, стоящих при x2 и x4 меньше 0,05, то они не значимы. К аналогичному выводу можно прийти, воспользовавшись t-критерием: t2(10)=-0,013 и t3(10)=1,44
С учетом этого факта, пересчитаем уравнение множественной регрессии, выбрав в качестве зависимой (dependent) переменную y и независимые (independent) переменные х1 и x3, коэффициенты при которых значимы:
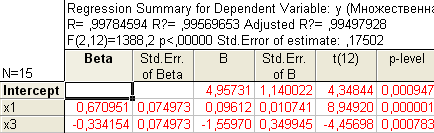
Т.о., уравнение регрессии имеет вид
Для выполнения прогнозов по полученному уравнению необходимо показать, что регрессионная модель адекватна результатам наблюдений. С этой целью можно воспользоваться критерием Дарбина-Уотсона, согласно которого, рассчитанный системой Statistica коэффициент dрасч необходимо сравнить с табличным значением dтабл (для совокупности объемом n=15, уровня значимости =0,05 и трех оцениваемых параметров регрессии, значение dтабл=1,75). Если dрасч>dтабл, то полученная модель адекватна и пригодна для прогнозирования. Для определения dрасч в Statistica в окне Residual Analysis на вкладке Advanced необходимо выбрать опцию Durbin-Watson statistic:
В случае, когда модель адекватна результатам наблюдения для выполнения прогноза в окне Multyple Regression Results вкладки Residuals/assumptions/prediction (Остатки/Предположения/Прогнозирование) выбрать опцию (прогнозирование зависимой переменной). Например, если в Москве среднегодовую стоимость основных фондов (переменная x1) повысить на 50 тыс. руб., а трудоемкость единицы продукции (переменная х3) уменьшить в два раза, то следует ожидать производительности труда равной 19,16 (увеличится на 19,16-14=5,16):
Источник: studfile.net
Как в программе Statistica корреляцию делать? Где её искать?
Корреляция в программе Статистика проводится, если уже готова таблица с данными, которые надо проверить на корреляцию. Естественно, что сразу после этого появляется вопрос Как делать корреляцию? Попробую объяснить этот процесс более-менее популярно.
Открываете окно редактора программы Статистика, вам здесь предложат создать новый документ. Создайте его и скопируйте данные своей таблицы в таблицу редактора. Лучше это сделать из Эксель.
Затем выбираете меню «Статистика». Откроется список с опциями. Выбирайте здесь статистическую методику, которую вы будете использовать. Например: регрессионный анализ, дисперсионный анализ, непараметрические критерии.
Например, выбираете «Непараметрические критерии». После щелчка на этой опции откроется диалоговое окно (ДО) с предложением выбрать непараметрическую методику. Выбирайте например «Спирмен».
Откроется следующее ДО — тут тоже жмите кнопку «Спирмен», после этого откроется еще одно ДО с таблицей рядов и столбцов. Выбирайте какие ряды вы будете сравнивать между собой. (Ряды определяются по вашей таблице в Экселе). Например, вы будете сравнивать «Возраст» (Val 1) и «Желание учиться» (Val 5). Выделяйте эти строки. Жмите на кнопку «Старт».
После этого программа вам автоматически выдает окно с коэффициентом корреляции, по которому можно сделать вывод, что учиться в 20 лет, действительно, совершенно не хочется!
В общем очень интересная программа!
Источник: www.bolshoyvopros.ru
Корреляции в Стате: Пирсон, Спирмен и Кендалл
В статистике корреляция относится к силе и направлению связи между двумя переменными. Значение коэффициента корреляции может варьироваться от -1 до 1, где -1 указывает на полную отрицательную связь, 0 указывает на отсутствие связи и 1 указывает на полную положительную связь.
Существует три распространенных способа измерения корреляции:
Корреляция Пирсона: используется для измерения корреляции между двумя непрерывными переменными. (например, рост и вес)
Корреляция Спирмена: используется для измерения корреляции между двумя ранжированными переменными. (например, оценка балла учащегося на экзамене по математике и оценка его оценки на экзамене по естественным наукам в классе)
Корреляция Кендалла: используется, когда вы хотите использовать корреляцию Спирмена, но размер выборки мал и имеется много связанных рангов.
В этом руководстве объясняется, как найти все три типа корреляций в Stata.
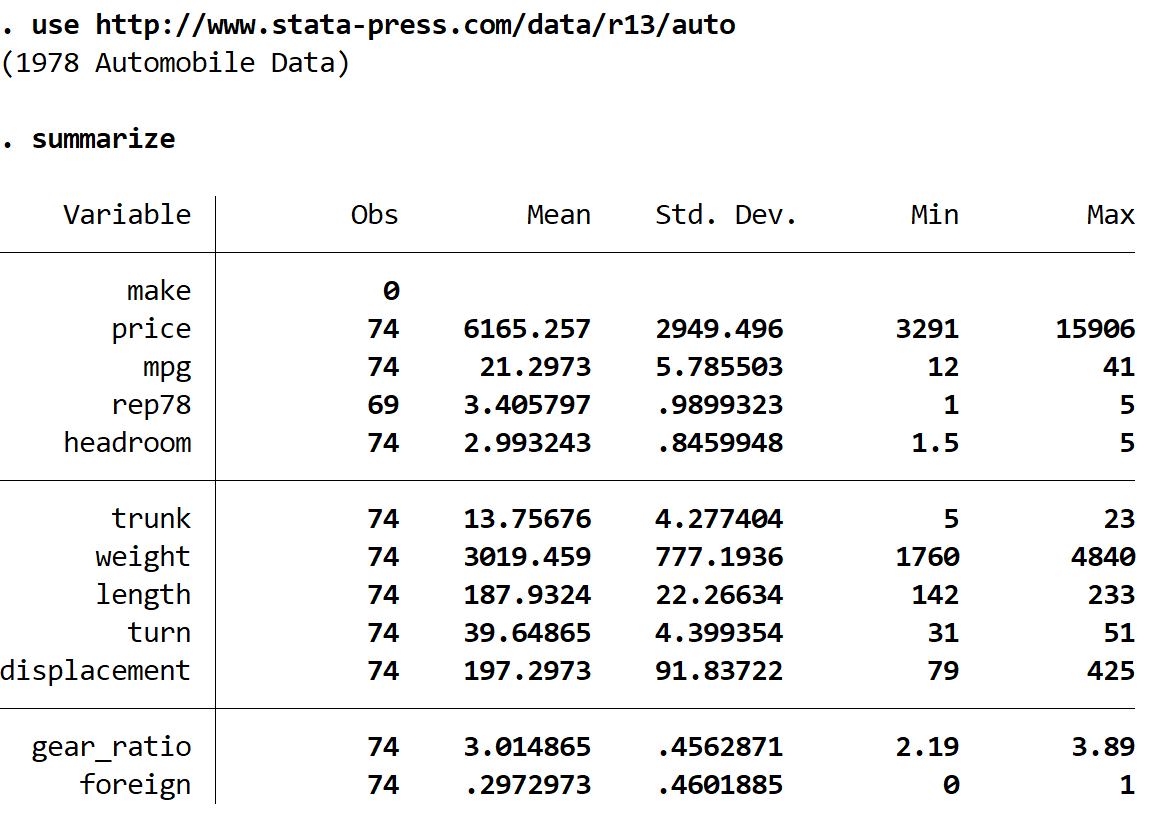
Загрузка данных
Для каждого из следующих примеров мы будем использовать набор данных с именем auto.Вы можете загрузить этот набор данных, введя следующее в поле Command:
используйте http://www.stata-press.com/data/r13/auto